1. INTRODUCCIÓN El flujo en un canal aluvial es de tipo no permanente y no uniforme. En consecuencia, la descarga de agua y sedimentos varía en el tiempo y el espacio. En un tramo de canal, los flujos de equilibrio se definen como aquéllos en los que la afluencia de sedimentos y el flujo de salida se equilibran durante un período de tiempo suficientemente largo. La resistencia, el transporte de material del lecho y las relaciones morfológicas se basan generalmente en condiciones de flujo de equilibrio. Las desviaciones de la condición de equilibrio provocan la formación de perturbaciones en la superficie del lecho, las cuales viajan aguas abajo en un flujo subcrítico y están sujetos a disipación. El régimen asociado con estas perturbaciones, o el régimen de transición entre dos estados de equilibrio, se denomina onda de lecho (8). Entre las causas de la formación de ondas de lecho se encuentran las siguientes: (1) Variación en el suministro de sedimentos aguas arriba a un tramo de canal; (2) cambio en la capacidad de transporte del material del lecho, provocada por un cambio en las condiciones hidráulicas; y (3) efecto del dragado y excavaciones del lecho sobre las condiciones de transporte del material del lecho. El estudio de la propagación de onda del lecho puede abordarse desde un punto de vista analítico o numérico. El enfoque analítico (4) se puede utilizar para estudiar ciertos tipos de ondas, pero los supuestos son demasiado exigentes en el caso general. Por otro lado, los modelos numéricos generalmente se pueden construir utilizando un número menor de supuestos y son más versátiles que las soluciones analíticas en la especificación de condiciones de frontera. Por lo tanto, un modelo numérico se considera una herramienta más eficaz en el estudio de la propagación de ondas del lecho móvil. Las cuestiones asociadas de estabilidad, consistencia y convergencia surgen cada vez que se realiza un proyecto de modelado numérico. Sin embargo, la experiencia con este tipo de modelos en las dos últimas décadas indica que estas dificultades pueden ser controladas.
Un modelo numérico implica la solución de una o más ecuaciones diferenciales parciales mediante el uso de técnicas de diferencias finitas. En el problema del lecho móvil, hay tres ecuaciones: Una alternativa práctica al método de enrutamiento secuencial para los casos en los que las ondas del lecho son de interés principal viene dada por el método de descarga conocida. El fundamento de este método de solución radica en que las ondas del lecho se propagan a un ritmo mucho más lento que las ondas de la superficie del agua. Por lo tanto, dentro de un intervalo de tiempo, se puede suponer que se mantiene un caudal de agua constante. Cabe señalar que el supuesto de caudal de agua constante en los modelos transitorios de lecho es análogo al supuesto de un límite rígido en los modelos de enrutamiento de crecidas (4). El supuesto de caudal de agua permanente sugiere que la ecuación de continuidad del agua se describa mediante una relación algebraica simple. Por lo tanto, solo quedan dos ecuaciones diferenciales: (1) Ecuación de continuidad del sedimento; y (2) ecuación de movimiento. Además, la omisión del término de aceleración local de la ecuación de movimiento se deriva directamente del supuesto de caudal de agua permanente. Al igual que con los modelos de enrutamiento de avenidas basados en la onda cinemática, la naturaleza no permanente del problema se conserva a través del término de cambio temporal en la ecuación de continuidad.
En este artículo se presenta un modelo de onda de lecho de descarga conocida. El modelo representa una mejora con respecto a los modelos anteriores del mismo tipo en el sentido de que se evita la inestabilidad debida a la mala colocación de la función de transporte de material del lecho (6) y se evitan los errores en la conservación de la masa debidos a la formulación incorrecta de la condición de frontera (3). mediante el uso de una formulación estrictamente no lineal. Tres limitaciones del modelo matemático son evidentes desde el principio. La formulación unidimensional no permite la descripción de meandros. Además, dado que no se prevé el tránsito de los sedimentos por fracciones de tamaño, no se pueden tener en cuenta los fenómenos de acorazamiento. Además, la función de transporte no tiene en cuenta efectivamente la condición de movimiento incipiente; por lo tanto, el modelo funcionaría mejor cuando las condiciones de flujo sean tales que el número de Froude sea mayor que 0.1.
El resto del presente artículo trata los siguientes temas en detalle: (1) Ecuaciones de gobierno; (2) esquema de diferencias finitas; (3) condiciones de frontera; (4) estabilidad y convergencia; y (5) experimentos numéricos.
2. ECUACIONES DE GOBIERNO
Las ecuaciones de gobierno, expresadas por unidad de ancho, son la continuidad del sedimento:
∂qs ∂ ∂z
1 ∂u ∂ u 2 ∂d ∂z
Según Mahmood y el primer autor (8), en el flujo de un río, el término de variación de concentración temporal en la Ec. 1 es muy pequeño en comparación con los términos restantes; por lo tanto, aquí se omite. Además, el término de aceleración local en la Ec. 2 se omite sobre la base de que el supuesto de caudal constante no justifica su inclusión (4). Haciendo q = ud, en el cual q = caudal líquido, constante, las Ecs. 1 y 2 se reducen a:
∂qs ∂z
q 2 ∂ ∂d ∂z
Se necesitan dos ecuaciones complementarias para resolver el sistema de Ecs. 3 y 4:
Las funciones de resistencia y transporte utilizadas aquí son las siguentes:
Para un canal ancho, ƒr = f /8, en la cual f = factor de fricción de Darcy-Weisbach.
3. ESQUEMA DE DIFERENCIAS FINITAS
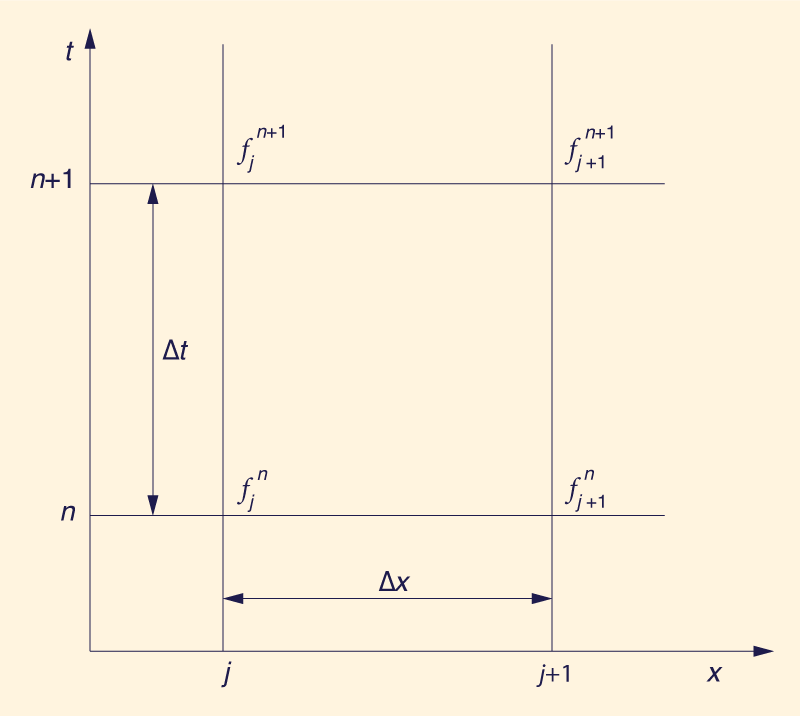
Aquí se utiliza el esquema implícito de cuatro puntos de Preissmann (6). El esquema está expresado por los siguientes operadores (Fig. 1):
en la cual ƒ = variable dependiente, y θ = factor de ponderación del esquema implícito.
La aplicación de las Ecs. 7-9 a las Ecs. 3 y 4 en forma discreta en el plano x - t produce un conjunto de ecuaciones algebraicas no lineales. Para resolver los valores de las variables dependientes en el nivel avanzado de tiempo sin recurrir a un proceso iterativo, se diseña un esquema de linearización. Este esquema permite la conversión de un sistema de ecuaciones no lineales en un sistema de ecuaciones lineales que se puede resolver directamente, sin iteración. El esquema de linearización genera errores adicionales a los ya impuestos por la solución discreta. Sin embargo, el tamaño y el crecimiento de estos errores se pueden controlar de manera efectiva permaneciendo dentro de los límites del método computacional, es decir, evitando cambios bruscos en los valores de las variables dependientes. En términos de efectividad, el esquema de solución linearizada se compara favorablemente con respecto a la solución no lineal.
El esquema de linearización tiene la siguiente forma:
en la cual δ = número real.
La solución del sistema de ecuaciones lineales simultáneas se logra mediante el conocido algoritmo de doble barrida (6).
4. CONDICIONES DE CONTORNO
En la frontera aguas arriba, se puede especificar el cambio en el nivel o la elevación del lecho con el tiempo. Alternativamente, se puede especificar la profundidad del flujo. Esto permite el modelado de un hidrograma de flujo de entrada de sedimentos, al relacionar éste con el cambio en la profundidad del flujo. Para diferentes descargas de agua y sedimentos, la condición de frontera aguas arriba se formula como sigue (7):
en las cuales ∆d1T = cambio en la profundidad de flujo en la condición de frontera aguas arriba; ∆d1S = cambio en la profundidad de flujo en la condición de frontera aguas arriba debido a la entrada de sedimentos en desequilibrio; y ∆d1Q = cambio en la profundidad de flujo en la condición de frontera aguas arriba debido a la entrada de agua en desequilibrio. Para la descarga de agua constante en el tiempo, la Ec. 11 se reduce a lo siguiente:
Las Ecuaciones 11 y 12 se basan en la ecuación de transporte de material del lecho (Ec. 6) y son estrictamente de tipo no lineal. Una comparación entre esta formulación y otra basada en una linealización en la frontera [ver Cunge y Perdreau (3)] muestra que la primera es intrínsecamente precisa, mientras que la última puede resultar en errores graves en la frontera. La condición de frontera aguas abajo se da generalmente como una relación caudal-tirante. Para el caso de caudal constante, el tirante aguas abajo generalmente se mantiene constante. 5. ESTABILIDAD Y CONVERGENCIA
Todo modelo numérico debe satisfacer ciertos requisitos de estabilidad y convergencia.
El primer autor, et al. (10) han presentado un análisis exhaustivo de las propiedades numéricas de los modelos transitorios de lecho implícito. Según este estudio, el comportamiento del modelo está controlado por tres parámetros numéricos y dos físicos. Los parámetros numéricos son:
Los parámetros físicos son: (1) Número de Froude del flujo de equilibrio Fo, definido como
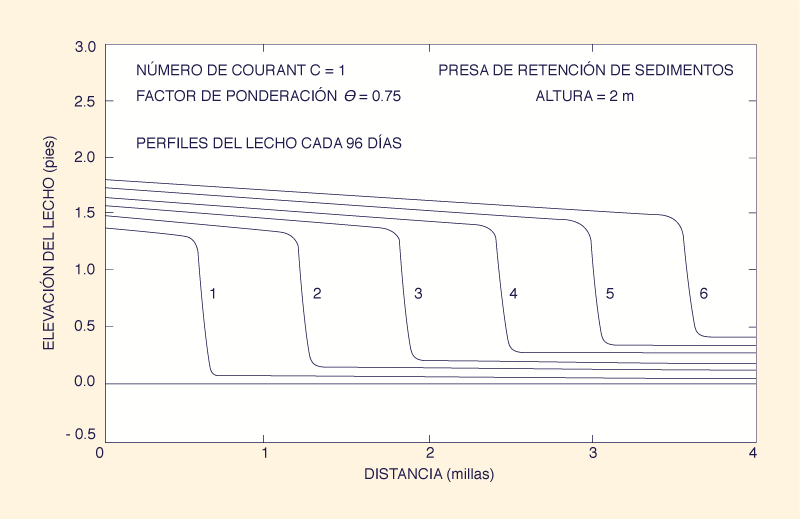
6. EXPERIMENTOS NUMÉRICOS Los experimentos numéricos tienen como objetivo evaluar el comportamiento general del modelo, medido por su capacidad para simular problemas transitorios hipotéticos, los cuales producen soluciones físicamente reales. Además, la experimentación numérica se utiliza para verificar el análisis teórico de estabilidad y convergencia. Formación de ondas de arena. Las ondas de arena se definen como acumulaciones transitorias de sedimentos en el lecho de un río. Se sabe que varios fenómenos como inundaciones, deslizamientos de tierra y fallas de presas provocan la formación de ondas de arena. Una vez que se ha formado la onda, se traslada lentamente aguas abajo en condiciones de flujo subcrítico. El modelo matemático presentado en este artículo simula efectivamente la formación de ondas de arena. Un hidrograma de carga de material del lecho que no está en equilibrio (en exceso o defecto de la velocidad de transporte de equilibrio) crea una onda de arena positiva (agradación) o negativa (degradación) a medida que ingresa al canal. El proceso de formación de ondas de arena está sujeto a una restricción numérica: el número de Courant C del lecho móvil debe ser igual o mayor que uno. De lo contrario, se presentan oscilaciones parasitarias en el modelo y, finalmente, la solución pierde sentido. Por lo tanto, al modelar la formación de ondas de arena, es de suma importancia tener un conocimiento previo de la rapidez de la perturbación del lecho (4). Con la celeridad conocida al menos aproximadamente, se verifica el número de Courant del lecho para asegurarse de que se cumpla la restricción numérica: C ≥ 1. Migración de ondas de arena. Las ondas de arena migran aguas abajo en un flujo subcrítico y están sujetas a disipación. La cantidad de disipación observada en el modelo numérico suele ser la combinación de dispersión física y numérica. La cantidad de dispersión numérica es una indicación de la convergencia de la solución; la solución será más convergente a medida que se minimice la dispersión numérica. En general, esto se puede lograr utilizando una resolución espacial L/∆x tan alta como sea posible, un número Courant próximo a 1, y un valor del factor de ponderación en el rango 0.5 ≤ θ ≤ 0.75. Sin embargo, la estabilidad puede verse afectada si se busca la eliminación de toda la dispersión numérica; por lo tanto, en la práctica, puede ser necesario mantener una pequeña cantidad de dispersión numérica. Ondas de lecho de erosión y deposición. El modelo matemático se puede utilizar para estudiar varios fenómenos transitorios de erosión y de deposición. La Figura 2 muestra el caso de una presa de retención de sedimentos. Este fenómeno transitorio se simula incrementando el tirante aguas abajo para reflejar la presencia de la presa. Esto provoca un aumento en el tirante en las secciones aguas arriba, reduciendo las velocidades de flujo y produciendo deposición. Una onda de arena se deposita en el extremo aguas arriba del tramo y migra aguas abajo lentamente, llenando eventualmente todo el volumen de retención.
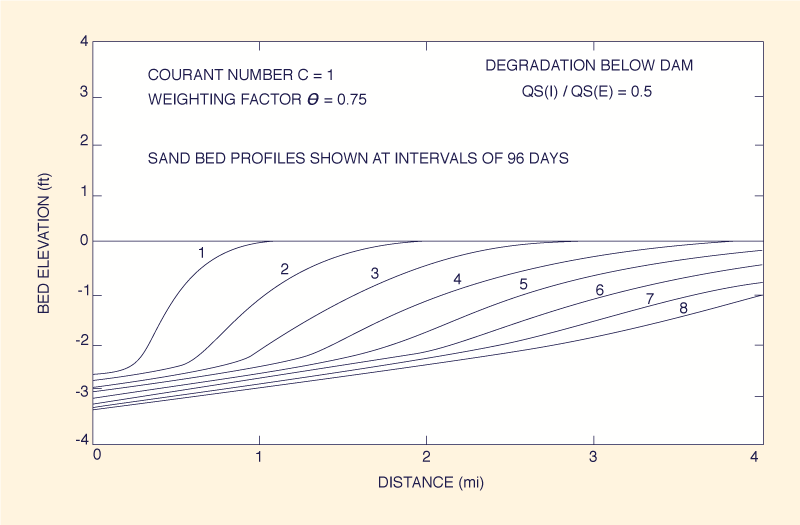
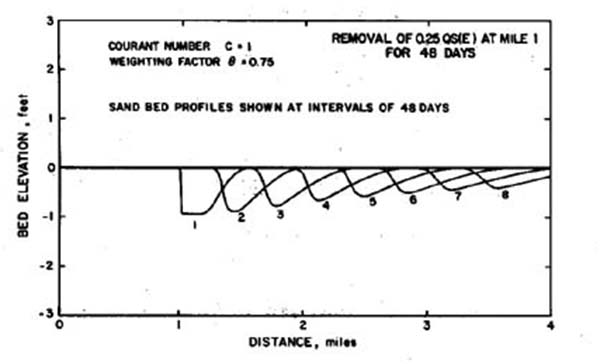
Otros ejemplos de formación y propagación de ondas, como el proceso de degradación debajo de una presa (Fig. 3) y el comportamiento de cortes de dragado y hoyos de préstamo (Fig. 4), se pueden estudiar de manera similar utilizando el modelo matemático aquí desarrollado.
Modelado de caudal variable. Para modelar un flujo de entrada de caudal variable en la frontera aguas arriba, el hidrograma se discretiza en varios intervalos. Se hace que cada intervalo del hidrograma corresponda a uno o más intervalos de la onda del lecho. La simulación del caudal líquido se logra mediante un cálculo de remanso entre los intervalos de tiempo de la onda del lecho.
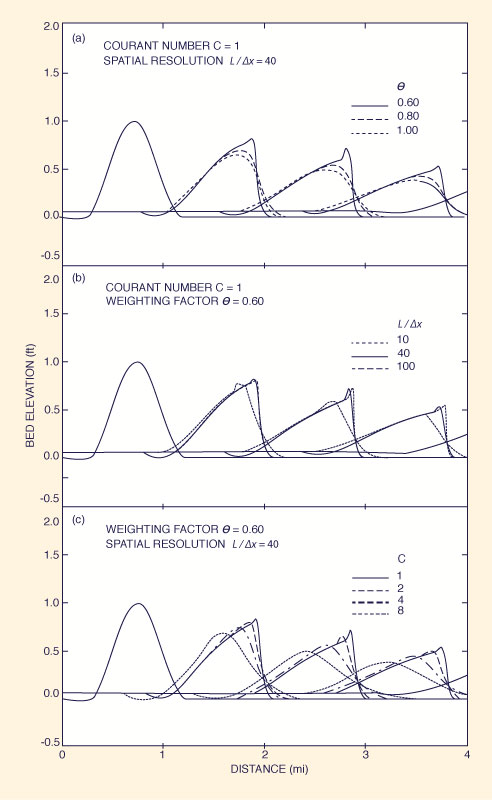
Sensibilidad a los parámetros numéricos. Se diseñó una serie de simulaciones de prueba con el propósito de evaluar la sensibilidad del modelo a los parámetros numéricos. El problema es el de rastrear la traslación y atenuación de una onda de arena sinusoidal a medida que viaja aguas abajo en un canal de ancho unitario. Los parámetros físicos se establecieron como sigue: Fo = 0.167, y
Las Figuras 5 (a) a 5 (c) muestran los resultados de la prueba numérica. La Figura 5 (a) muestra que cuanto mayor es el valor de θ, más estable es el modelo, es decir, mayor es la dispersión numérica. Un valor de θ = 0.6 muestra un patrón débil de inestabilidad.
Recomendaciones sobre estabilidad y convergencia. Valores en el rango 0.5 ≤ θ ≤ 0.6 pueden resultar en una solución débilmente estable o inestable. Como regla general, la estabilidad requiere que θ > 0.6. Se recomienda un valor de θ = 0.75, siempre que se utilice junto con una resolución espacial suficientemente alta (L/∆x ≥ 40) y un número de Courant, mayor que 1 lo más bajo posible. Un valor de C ≥ 1 es necesario para evitar oscilaciones debido a una mala posición de la condición de frontera aguas arriba. El segundo autor (7) ha derivado un criterio de convergencia aproximado basado en simulaciones numéricas. Definió un parámetro de convergencia Cp como sigue:
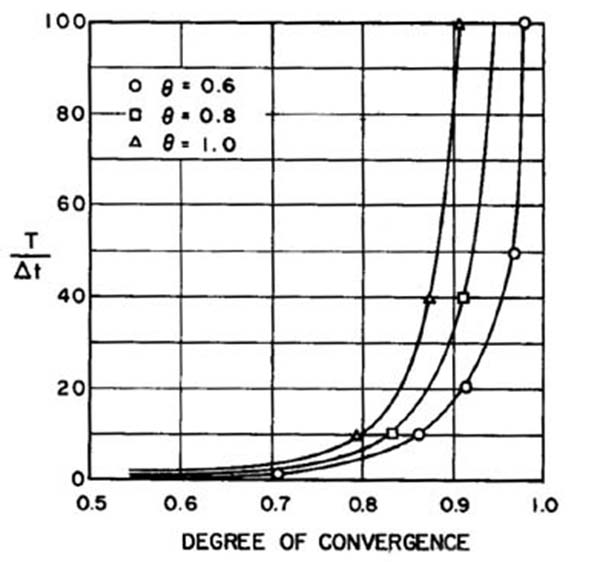
Valores altos de Cp resultan en una buena convergencia; por el contrario, valores bajos de Cp son un indicativo de poca convergencia. Un límite inferior de Cp puede estar dictado por consideraciones de precisión, mientras que un límite superior puede ser necesario desde el punto de vista económico. La Ecuación 16 también se puede expresar de la siguiente manera:
La Figura 6 muestra los resultados del análisis de convergencia. El grado de convergencia se define como la relación entre la celeridad numérica y la analítica, para soluciones numéricas en las cuales se varían T/∆t y θ. La Figura 6 resalta la importancia de la resolución temporal T /∆t como el parámetro de convergencia primario, a la vez que muestra el rol secundario del factor de ponderación θ. El rango recomendado para la resolución temporal es el siguiente: 20 ≤ T/∆t ≤ 100. Los valores de rango medio representarán una compensación entre precisión y limitaciones de costo.
7. RESUMEN Y CONCLUSIONES Se desarrolla un modelo matemático para simular la formación y propagación de ondas transitorias del lecho en canales. El modelo es del tipo de caudal conocido, es decir, dentro de un intervalo de tiempo, el caudal líquido se considera constante. Esta técnica permite el modelado numérico implícito de la propagación de ondas transitorias del lecho, utilizando intervalos de tiempo mayores de lo que sería posible utilizando el método de enrutamiento secuencial convencional.
La inestabilidad debida a la mala posición de la función de transporte de sedimentos se evita utilizando una función potencial entre la descarga del material del lecho y la velocidad media del flujo. Los errores en la conservación de la masa debido a una linealización en la frontera se eliminan mediante el uso de una formulación no lineal de la condición de frontera aguas arriba. La estabilidad y la convergencia son analizadas, estableciéndose criterios para asegurar la mejor operación del modelo. En particular, se muestra que la convergencia es principalmente una función de la resolución temporal T/∆t, con el factor de ponderación θ desempeñando un papel secundario. APÉNDICE I. BIBLIOGRAFÍA
APÉNDICE II. SIMBOLOGÍA En este artículo se utilizan los siguientes símbolos:
C = lecho transitorio número de Courant, coeficiente de Chézy;
Cg = coeficiente de transporte del material del lecho;
Cp = parámetro de convergencia, Ecs. 16 y 17;
Cs = concentración espacial de material del lecho;
d = profundidad de flujo;
do = profundidad de flujo de equilibrio;
Fo = número de Froude del flujo de equilibrio;
ƒ = variable dependiente;
ƒr = factor de fricción;
f = factor de fricción de Darcy-Weisbach;
g = aceleración de la gravedad;
j = índice de discretización espacial;
L = longitud característica de la onda;
L/∆x = resolucion espacial;
m = exponente en la función de transporte de material del lecho;
n = índice de discretización del tiempo;
p = porosidad del lecho;
q = caudal líquido constante;
qs = descarga del material del lecho;
qsL = entrada lateral de sedimentos;
Sf = pendiente de fricción;
So = pendiente de fondo;
T = duración característica de la onda transitoria;
T/∆t = resolución temporal;
t = variable de tiempo;
u = velocidad media;
x = variable de espacio;
z = elevación del fondo referida a una referencia arbitraria;
∆d1Q = cambio en la profundidad de flujo en la frontera aguas arriba debido a una entrada de agua no equilibrada;
∆d1S = cambio en las profundidades del flujo aguas arriba debido a la entrada de sedimentos en desequilibrio;
∆d1T = cambio total en la profundidad de flujo en la frontera aguas arriba;
∆ƒ = cambio de variable ƒ ;
∆t = intervalo de tiempo;
∆x = intervalo de espacio;
δ = un número real;
θ = factor de ponderación del esquema implícito;
ρs = densidad de partículas de sedimento; y
σ* = número de onda adimensional. |
| 211231 |
| Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader. |