|
RESUMEN
Las caracter�sticas de propagaci�n de varios tipos de ondas poco profundas en el flujo de un canal abierto son calculadas sobre la base de la teor�a de la estabilidad lineal. Se deriva las funciones de celeridad y atenuaci�n de las ondas cinem�tica, difusiva, din�mica permanente,
din�mica y de gravedad. Para el caso m�s general, es decir, el modelo de onda din�mica, las caracter�sticas de propagaci�n son expresadas en funci�n del n�mero de Froude del flujo uniforme permanente y el n�mero de onda adimensional del componente no permanente del movimiento. Para el modelo din�mico, el espectro del n�mero de onda se divide en tres grupos: (1) Un grupo de gravedad, que corresponde a un n�mero de onda grande, donde la celeridad es la celeridad de la onda de gravedad; (2) un grupo cinem�tico, que corresponde a un n�mero de onda peque�o, donde la celeridad es la celeridad de la onda cinem�tica; y (3) un grupo din�mico, que corresponde a los valores medios del espectro, donde la celeridad se encuentra entre los valores
de celeridad cinem�tica y de gravedad.
|
1. INTRODUCCI�N
A trav�s de los a�os, varios investigadores han intentado aclarar el fen�meno de la propagaci�n de ondas poco profundas en el flujo en un canal abierto. Quiz�s el m�s esclarecedor de estos estudios es el reportado en el art�culo cl�sico de Lighthill y Whitham, que analiz� en detalle el concepto de onda cinem�tica y lo contrast� con el de onda din�mica (5). La f�rmula de Lagrange para la celeridad de las ondas de gravedad poco profundas tambi�n ha sido objeto de considerable atenci�n en la literatura (3). A pesar de los avances logrados en la comprensi�n del fen�meno f�sico, a�n no se ha formulado una teor�a coherente que explique tanto la celeridad como las caracter�sticas de atenuaci�n. En este sentido, la teor�a de la estabilidad lineal puede ser utilizada como una herramienta eficaz no solo para proporcionar un an�lisis de primera aproximaci�n, sino tambi�n para revelar informaci�n valiosa sobre la f�sica subyacente del problema (6).
El an�lisis que aqu� se presenta aplica la teor�a de la estabilidad lineal al conjunto de ecuaciones que gobiernan el movimiento del flujo en canales abiertos. Las ecuaciones son las denominadas ecuaciones de Saint Venant, que son expresiones anal�ticas de los principios de conservaci�n de masa y momento (1). Las conclusiones se refieren a la magnitud de la celeridad y atenuaci�n de varios tipos de ondas en aguas poco profundas, expresadas como una funci�n del n�mero de Froude del flujo uniforme permanente y un n�mero de onda adimensional del componente no permanente del movimiento.
2. ECUACIONES DE GOBIERNO
Las ecuaciones que gobiernan el flujo no permanente unidimensional en canales anchos de secci�n transversal rectangular, expresadas por unidad de ancho de canal, son la ecuaci�n de continuidad (4):
∂d ∂u ∂d
u ____ + d ____ + ____ = 0
∂x ∂x ∂t
| (1) |
y la ecuaci�n de movimiento (2):
1 ∂u u ∂u ∂d
____ _____
+ ____ _____ + _____ + (Sf - So ) = 0
g ∂t g ∂x ∂x
| (2) |
en el cual u = velocidad media en una secci�n vertical; d = profundidad del flujo; g = aceleraci�n de la gravedad; Sf = pendiente de fricci�n; y So = pendiente de fondo.
La pendiente de fricci�n Sf est� directamente relacionada con el esfuerzo cortante de fondo τ por la expresi�n (2):
en la cual γ = peso unitario del agua.
Siguiendo la forma habitual de los c�lculos de estabilidad, las Ecs. 1 y 2 deben satisfacer el flujo no perturbado para el cual u = uo; d = do; y τ = τo, as� como el flujo perturbado para el cual u = uo + u' ; d = do + d' ; y τ = τo + τ' (7).
El super�ndice en las variables de flujo representa una peque�a perturbaci�n del flujo uniforme permanente. Por lo tanto, todos los t�rminos cuadr�ticos de las componentes fluctuantes pueden despreciarse debido a un razonamiento de orden de magnitud.
La sustituci�n de las variables de perturbaci�n en las Ecs. 1, 2, y 3, despu�s de linealizar, lleva a lo siguiente (5):
∂d' ∂u' ∂d'
uo ____ + do ____ + ____ = 0
∂x ∂x ∂t
| (4) |
1 ∂u' uo ∂u' ∂d' τ' d'
____ _____
+ ____ _____ + _____ +
So ( _____ - _____ ) = 0
g ∂t g ∂x ∂x τo do
| (5) |
en la cual:
El esfuerzo cortante τ puede relacionarse con la velocidad media de la siguiente forma:
en la cual:
El valor Cf es el coeficiente de Chezy; y ρ = densidad del agua. Considerando la Ec. 7, la Ec. 5 se puede reescribir como sigue:
1 ∂u' uo ∂u' ∂d' u' d'
____ _____
+ ____ _____ + _____ +
So ( 2 _____ - _____ ) = 0
g ∂t g ∂x ∂x uo do
| (9) |
En la mayor�a de las aplicaciones pr�cticas, se prefiere la ecuaci�n de Manning a la ecuaci�n de Chezy. Esta �ltima, sin embargo, tiene la ventaja de la no dimensionalidad, y es por esta raz�n que se usa aqu�. Adem�s, la constante Cf es consistente con el supuesto de una peque�a perturbaci�n.
3. MODELOS DE ONDA
La propagaci�n de las ondas en aguas poco profundas est� controlada por el balance de las diversas fuerzas incluidas en la ecuaci�n de movimiento. En la Ec. 2, el primer t�rmino representa la inercia local, el segundo la inercia convectiva, el tercer t�rmino la diferencia de presiones y el cuarto representa la fricci�n y la pendiente de fondo. Se pueden construir varios modelos de onda, dependiendo de cu�l de estos cuatro t�rminos se considere insignificante en comparaci�n con los t�rminos restantes.
La siguiente tabla proporciona una referencia r�pida a los distintos modelos de ondas que son reconocidos en la pr�ctica.
T�rmino I II III IV
Ecuaci�n 1 ∂u u ∂u ∂d
de movimiento ____ _____
+ ____ _____ + _____ + (Sf - So ) = 0
g ∂t g ∂x ∂x
| (2) |
El modelo de onda y los t�rminos usados para describirlo son: (1) Onda cinem�tica IV; (2) onda de difusi�n III + IV; (3) onda din�mica permanente II + III + IV; (4) onda din�mica I + II + III + IV; y (5) onda de gravedad I + II + III.
4. AN�LISIS DE PEQUE�AS PERTURBACIONES
Con el fin de proporcionar una forma conveniente de tener en cuenta expl�citamente los diversos modelos de onda, la Ec. 9 queda redefinida como:
l ∂u' auo ∂u' ∂d' u' d'
____ _____
+ _____ _____ + p _____ + k So ( 2 _____ - _____ ) = 0
g ∂t g ∂x ∂x uo do
| (10) |
en el cual l, a, p, y k son n�meros enteros y pueden tomar valores de 0 a 1 solamente, dependiendo de qu� t�rminos de la Ec. 9 se utilicen para describir el movimiento.
La soluci�n para una peque�a perturbaci�n se postula en la siguiente forma exponencial:
d'
____ = d* e i (σ* x* - β* t* )
do
| (11) |
en la cual d' es una peque�a perturbaci�n a do; d* es una funci�n adimensional de amplitud de profundidad; σ* es un n�mero de onda adimensional, β* es un factor de propagaci�n adimensional complejo, y x* and t* son coordenadas espaciales y temporales adimensionales tales que:
2 π
σ* = (
_____ ) Lo
L
| (12) |
2 π Lo
β*R = (
_____ ) _____
T uo
| (13) |
|
β*I = factor de propagaci�n de amplitud
| (14) |
en la cual L = longitud de onda de la perturbaci�n; y T = per�odo. El valor Lo = longitud horizontal en la cual el flujo uniforme permanente desciende una altura igual a su profundidad, definida como Lo =
do /So. La celeridad adimensional de la perturbaci�n viene dada por:
L / T β*R
c* =
________ = _______
uo σ*
| (17) |
La atenuaci�n de la onda sigue una ley exponencial en la cual la amplitud en un tiempo dado t = amplitud inicial en el tiempo to multiplicada por (e β*I t* ), en la cual t* = (t - to) uo / Lo. Cuando comparamos las amplitudes de onda despu�s de un per�odo de propagaci�n, el valor de t* es t* = T uo / Lo, o igualmente, t* = 2 π / | β*R |. El decremento logar�tmico δ se define como sigue: δ = β* T u o / Lo, o δ = 2 π β*I / | β*R | (10). El valor de δ es una medida de la velocidad a la que el componente no permanente del movimiento cambia con la propagaci�n. Para δ positivo, se produce amplificaci�n; para δ negativo, el movimiento (no permanente)
se aten�a y eventualmente desaparece.
La profundidad de perturbaci�n est� asociada con una velocidad de perturbaci�n de la forma:
u'
____ = u* e i (σ* x* - β* t* )
uo
| (18) |
en la cual u* es una funci�n adimensional de amplitud de velocidad. La sustituci�n de las Ecs. 11 y 18 en las Ecs. 4 y 10 lleva, respectivamente, a lo siguiente:
σ* u*
+ (σ* - β* ) d* = 0
| (19) |
[ 2k + i Fo2 (α σ* -
l β* ) ] u*
+ (i p σ* - k ) d* = 0
| (20) |
en la cual:
uo 2
Fo2 = ______
g do
| (21) |
Las ecuaciones 19 y 20 constituyen un sistema homog�neo de ecuaciones lineales con las inc�gnitas u* and d*. Para que la soluci�n no sea trivial, el determinante de la matriz de coeficientes debe anularse. En consecuencia:
i l β* 2 Fo2 - i
σ*2 (p - a Fo2 ) + 3 k σ* -
2 k β* - i σ* β* (l + a) Fo2 = 0
| (22) |
La Ec. 22 es la ecuaci�n caracter�stica que gobierna la propagaci�n de ondas de peque�a amplitud. En el tratamiento que sigue, se realizan aproximaciones sucesivas para ajustarse a los diversos tipos de modelos de ondas considerados en la secci�n anterior.
5. MODELO DE ONDA CINEM�TICA
En el modelo de onda cinem�tica, los t�rminos de inercia y presi�n son despreciables en comparaci�n con los t�rminos de pendiente de fondo y de fricci�n.
En consecuencia, en la Ec. 22, l = a = p = 0; y k = 1, resultando en:
Dado que todos los t�rminos imaginarios se han eliminado en la Ec. 23, β*I = 0; y β*R = β*. El decremento logar�tmico δk es, entonces:
β*I
δk = 2π
_____ = 0
β*R
| (24) |
y la celeridad adimensional de la onda cinem�tica es:
β*R 3
c* k = _____ = ____
T 2
| (25) |
Las Ecuaciones 23-25 justifican las siguientes conclusiones con respecto a la propagaci�n de ondas cinem�ticas: (1) Dado que la Ec. 23 es de primer orden, las ondas cinem�ticas se propagan solo en la direcci�n aguas abajo; (2) la celeridad de una onda cinem�tica es independiente de Fo y σ* e igual a 1.5 veces la velocidad media del flujo; y (3) la atenuaci�n de una onda cinem�tica es cero, es decir, una onda cinem�tica se propaga aguas abajo sin disipaci�n.
6. MODELO DE ONDA DE DIFUSI�N
En el modelo de onda de difusi�n, los t�rminos de inercia se consideran despreciables, pero el t�rmino de presi�n se tiene en cuenta en los c�lculos. En consecuencia, en la Ec. 22, l = a = 0; p = k = 1, resultando en.
|
- i σ* 2 + 3 σ* - 2 β* = 0
| (26) |
3 σ* - i σ* 2
β* =
______________
2
| (27) |
y la celeridad de la onda de difusi�n es:
β*R 3
c*d = _____ = _____
σ* 2
| (28) |
El decremento logar�tmico de la onda de difusi�n es:
β*I σ*
δd = 2 π ______ =
- 2 π ( ____ )
β*R 3
| (29) |
Las siguientes conclusiones son aplicables a las ondas de difusi�n: (1) Debido a que la Ec. 26 es de primer orden en β*, las ondas de difusi�n se propagan s�lo aguas abajo, y su celeridad es independiente de Fo y σ* y es igual a 1.5 de la velocidad media del flujo; y (2) las ondas de difusi�n se aten�an a medida que se propagan aguas abajo, y la tasa de atenuaci�n es controlada por el n�mero de onda adimensional σ*. Cuanto mayor sea el n�mero de onda adimensional, mayor ser� la atenuaci�n.
7. MODELO DE ONDA DIN�MICA PERMANENTE
En el modelo de onda din�mica permanente, el t�rmino de inercia convectiva
se incluye en el problema, pero se desprecia el t�rmino de inercia local. En consecuencia, en la Ec. 22, l = 0; y a = p = k = 1, resultando en:
|
- i σ* 2 (1 - Fo2 ) + 3 σ* - 2 β* - i σ* β* Fo2 = 0
| (30) |
3 σ* - i σ*2 ( 1 - Fo2 )
β*
= _______________________
2 + i σ* Fo2
| (31) |
σ* [ 6 - σ*2 Fo2 ( 1 - Fo2 )] - i σ*2 ( 2 + Fo2 )
β*
= ___________________________________________
4 + σ*2 Fo4
| (32) |
De la Ecuación 32, la celeridad del modelo din�mico permanente es:
2 - σ* 2 Fo2
c*s
= 1 + ______________
4 + σ*2 Fo4
| (33) |
El decremento logar�tmico del modelo din�mico permanente es:
σ* ( 2 + Fo2 )
δs
= - 2 π ________________________
| 6 - σ*2 Fo2 ( 1 - Fo2 ) |
| (34) |
Las siguientes conclusiones son derivadas con respecto al modelo din�mico permanente: (1) La propagaci�n de la onda din�mica permanente es en una direcci�n, ya que la Ec. 30 es de primer orden en β*; y (2) las caracter�sticas de celeridad y atenuaci�n son funciones del n�mero de Froude Fo del flujo uniforme permanente y del n�mero de onda adimensional σ*.
8. MODELO DE ONDA DIN�MICA
En el modelo de onda din�mica, se consideran todos los t�rminos de la ecuaci�n de movimiento.
Por lo tanto, en la Ec. 22, l = a = p = k = 1.
Esto lleva a lo siguiemte:
|
Fo2 β*2 - 2 ( σ* Fo2 - i ) β* - [ σ*2 ( 1 - Fo2 ) + 3 σ* i ] = 0
| (35) |
La Ecuaci�n 35 es de segundo orden, lo que resulta en dos ra�ces. Desde el punto de vista f�sico, las ondas din�micas se propagan a lo largo de dos trayectorias caracter�sticas, que puede ser, ya sea: (1) una, aguas arriba y otra, aguas abajo; o (2) ambas aguas abajo. En el caso de que la propagaci�n se d� en diferentes direcciones, es conveniente definir como onda primaria la onda que viaja aguas abajo, e identificar su celeridad y decremento logar�tmico como c*1 y δ1, respectivamente; la onda secundaria se define como la onda que viaja aguas arriba con celeridad c*2 y decremento logar�tmico δ2. En el caso de que ambas ondas viajen aguas abajo, la onda primaria es la onda m�s r�pida y la onda secundaria es la m�s lenta.
La soluci�n de la Ec. 35 es:
1
β* =
σ* ( 1 - i ζ ) + σ* [ ( ______ - ζ 2 ) + i ζ ] 1/2
Fo2
| (36) |
en la cual:
1
ζ =
_________
σ* Fo2
| (37) |
Una expresi�n similar a la Ec. 37 se conoce en la literatura como n�mero de flujo cinem�tico (9).
El argumento de la ra�z cuadrada compleja se puede expresar en forma polar como sigue:
|
A + i B = C ( cos θ + i sen θ )
| (38) |
en la cual:
1
A =
______ - ζ 2
Fo2
| (39) |
1
C = [ (
______ - ζ 2 ) 2 + ζ 2 ] 1/2
Fo2
| (41) |
y la ra�z del argumento complejo es:
θ + 2 k π θ + 2 k π
(A + i B )1/2 = C1/2 ( cos _________ + i sen __________ ) ; para k = 0,1
2 2
| (43) |
Usando las relaciones de �ngulo medio se obtiene:
1 + cos θ 1 - cos θ
(A + i B )1/2 = ± C1/2 [ ( __________ )1/2 + i ( __________ )1/2 ]
2 2
| (44) |
en la cual se ha hecho uso del caso en el que para ζ ≥ 0, θ/2 se encuentra en el primer cuadrante.
Desde que:
se concluye que:
C + A C - A
(A + i B )1/2 = ± [ ( ________ )1/2 + i ( ________ )1/2 ]
2 2
| (46) |
o bien:
C + A C - A
β* = σ* (1 - i ζ ) ± σ* [ ( ________ )1/2 + i ( ________ )1/2 ]
2 2
| (47) |
De la Ec. 47, se obtienen las siguientes dos ra�ces:
C + A C - A
β*1 = σ* [ 1 + ( ________ )1/2 ] - i σ* [ ζ - ( ________ )1/2 ]
2 2
| (48) |
C + A C - A
β*2 = σ* [ 1 - ( ________ )1/2 ] - i σ* [ ζ + ( ________ )1/2 ]
2 2
| (49) |
Definiendo:
C + A
D = (
_________ ) 1/2
2
| (50) |
y
C - A
E = (
_________ ) 1/2
2
| (51) |
las funciones de celeridad y atenuaci�n vienen dadas por las siguientes relaciones:
Para la onda primaria:
C + A
c*1 = 1 + (__________ ) 1/2
2
| (52) |
ζ - E
δ1 = - 2π _____________
| 1 + D |
| (53) |
Para la onda secundaria:
C + A
c* 2 = 1 - (
_________ ) 1/2
2
| (54) |
ζ + E
δ2 = - 2π ___________
| 1 - D |
| (55) |
| TABLA 1. Caracter�sticas de propagaci�n de ondas en aguas poco profundas en el flujo en canales abiertos.
|
Tipo de onda
(1) | Celeridad relativa c*r
(2) | Decremento logar�tmico δ
(3) |
| Cinem�tica |
1/2 |
0 |
| Difusi�n |
1/2
|
- 2 π ( σ* / 3 ) |
| Din�mica permanente |
( 2 - σ*2 Fo2 ) / ( 4 + σ*2 Fo4 ) |
- 2 π σ* ( 2 + Fo2 ) / | 6 - σ*2 Fo2 ( 1 - Fo2 ) | |
| (a) Din�mica
|
| Onda primaria |
+ [(C + A ) / 2 ] 1/2 |
- 2 π ( ζ - E ) / | 1 + D | |
| Onda secundaria |
- [(C + A ) / 2 ] 1/2 |
- 2 π ( ζ + E ) / | 1 - D | |
| (b) Gravedad
|
| Onda primaria |
+ 1 / Fo |
0 |
| Onda secundaria |
- 1 / Fo |
0 |
Notas: ζ = 1 / ( σ* Fo2 ) ; A = ( 1 / Fo2 ) - ζ 2 ; C = { [ ( 1 / Fo2 ) - ζ 2 ] 2 + ζ 2 } 1/2 ; D = [ (C + A ) / 2 ] 1/2 ;
E = [ (C - A ) / 2 ] 1/2 .
|
|
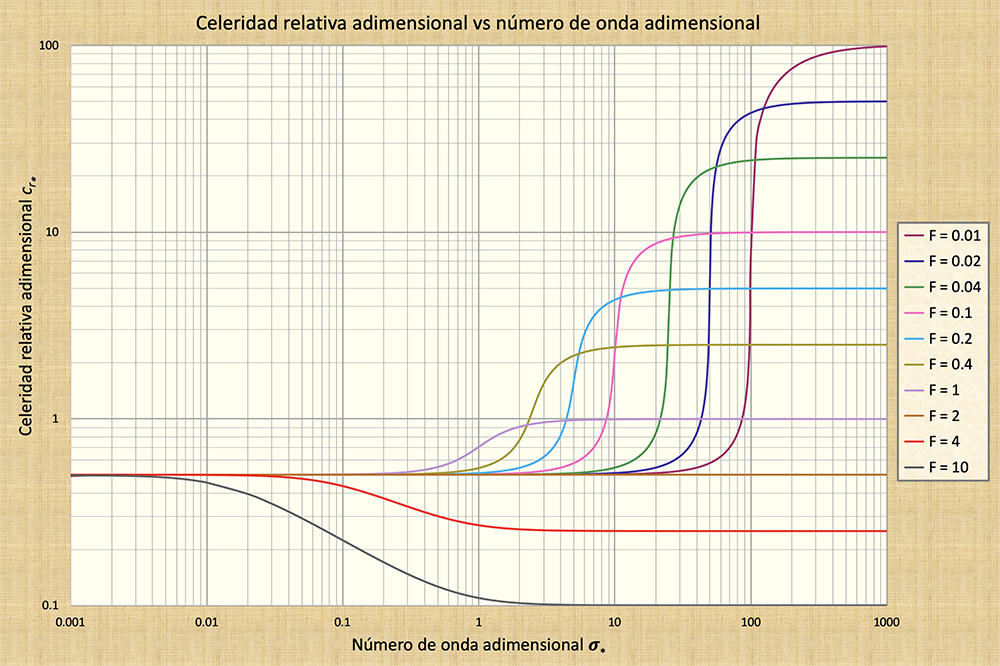
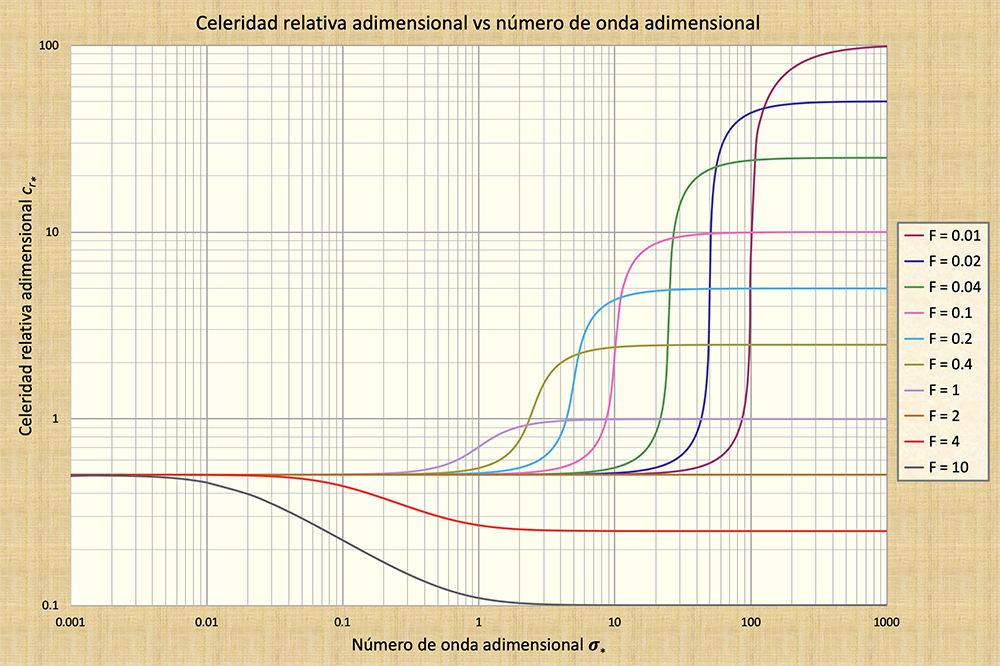
Fig. 1 Celeridad relativa adimensional c*r versus el n�mero de onda adimensional σ*;
par�metro de curva: n�mero de Froude Fo (0.01 ≤ Fo ≤ 10).
|
|
9. MODELO DE ONDA DE GRAVEDAD
En el modelo de onda de gravedad, los t�rminos de fricci�n y pendiente de fondo son excluidos de la ecuaci�n del momento. De ello se deduce que, en la Ec. 22, l =�a = p = 1; y k = 0, resultando en lo siguiente:
|
β*2 Fo 2 - 2 σ* β* Fo 2 - σ* 2 (1 - Fo 2 ) = 0
| (56) |
Dado que la Ec. 56 es de segundo orden en β* y no contiene t�rminos imaginarios, las ondas de gravedad tienen dos direcciones caracter�sticas y no est�n sujetas a atenuaci�n.
Resolviendo para β*R en la Ec. 56:
Fo 2 ± Fo
β*R = σ* (
___________ )
Fo 2
| (57) |
y la celeridad de una onda de gravedad est� dada por:
β*R 1
c* g = _____ = 1 ± _____
σ* Fo
| (58) |
o, de la forma m�s habitual de expresarlo (la f�rmula de Lagrange):
|
cg = uo ± ( g do )1/2
| (59) |
Las ondas de gravedad se propagan a lo largo de dos direcciones caracter�sticas. En el flujo subcr�tico, una direcci�n es aguas abajo con celeridad c1 = uo + (g do)1/2, y la otra es aguas arriba, con celeridad c2 = uo - (g do)1/2. En el flujo cr�tico, c1 = 2uo; y c2 = 0. En el flujo supercr�tico, ambas ondas viajan aguas abajo, con celeridades
c1 = uo + (g do)1/2; y c2 = uo - (g do)1/2.
La Tabla 1 contiene un resumen de las caracter�sticas de propagaci�n de las ondas. La celeridad que se muestra en la Tabla 1 es la celeridad relativa c* r , en la cual:
10. AN�LISIS DEL MODELO DE ONDA DIN�MICA
Las Ecuaciones 52-55 permiten calcular las caracter�sticas de propagaci�n del modelo de onda din�mica, en funci�n del n�mero de Froude Fo del flujo uniforme permanente y el n�mero de onda adimensional σ* de la perturbaci�n sinusoidal superpuesta.
La Figura 1 muestra los valores calculados de la celeridad relativa adimensional c*r versus el n�mero de onda adimensional σ* para n�meros de Froude entre 0.01-10. Se derivan las siguientes conclusiones:
Hay tres grupos bien definidos en el espectro del n�mero de onda: (a) un grupo cinem�tico correspondiente a valores peque�os del n�mero de onda σ*, en la cual la celeridad relativa c*r es independiente tanto de σ* como del n�mero de Froude Fo; (b) un grupo de gravedad correspondiente a valores grandes de σ*, en la cual c*r es independiente de σ* y depende �nicamente de Fo ; y (c) un grupo din�mico, en la que c*r es una funci�n tanto de σ* y Fo.
En el grupo cinem�tico, c*r se acerca asimptóticamente a 0.5, que corresponde al de una onda cinem�tica. En el grupo de gravedad, c*r se aproxima asint�ticamente al valor 1/Fo, que corresponde al de una onda de gravedad. En el grupo din�mico, c*r se encuentra entre los valores de celeridad de las ondas cinem�tica y de gravedad.
La ubicaci�n del grupo din�mico en el espectro de σ* es una funci�n de Fo.
Un corolario resultante de la Fig. 1 es que para Fo = 2, c*r = 0.5 para todos los valores de σ*. As�, para Fo = 2, todas las ondas, cinem�tica, din�mica y de gravedad, tienen celeridades iguales al valor cinem�tico. Las conclusiones de la Fig. 1 con respecto al valor l�mite de c*r , en los grupos cinem�tico y de gravedad se pueden obtener anal�ticamente con base en la teor�a de l�mites. Se puede demostrar que cuando σ* → ∞ , c*r → 1/Fo , y cuando σ* → 0, c*r → 0.5 (para Fo constante).
El c�lculo de los decrementos logar�tmicos δ1 y δ2 en funci�n de σ* y Fo, mediante las Ecs. 53 y 55
permite las siguientes conclusiones generales:
Para Fo < 2, las ondas primarias se propagan aguas abajo y se aten�an; para Fo = 2, las ondas primarias se propagan aguas abajo y no se amplifican ni aten�an en todo el espectro de σ*; para Fo > 2 las ondas primarias se propagan aguas abajo y se amplifican.
Para Fo < 1, las ondas secundarias se propagan aguas arriba
(c*r > 1), o aguas abajo (c*r < 1). Para F = 1, las ondas secundarias permanecen estacionarias (c*r = 1), o se propagan aguas abajo (c*r < 1). Para Fo > 1, las ondas secundarias se propagan aguas abajo. Las ondas secundarias se aten�an para todos los valores de Fo y σ*.
La Tabla 2 resume las conclusiones del p�rrafo anterior.
| TABLA 2. Caracter�sticas de celeridada y atenuaci�nb de la onda din�mica. |
N�mero de Froude
(1)
| Onda primaria
| Onda secundaria
|
c*1
(2)
| δ1
(3)
| c*2
(4)
| δ2
(5)
|
| Fo < 1
| +
| -
| -
| -
|
| +
| -
|
| Fo = 1
| +
| -
| 0
| -
|
| +
| -
|
| 1 < Fo < 2
| +
| -
| +
| -
|
| Fo = 2
| +
| 0
| +
| -
|
| Fo > 2
| +
| +
| +
| -
|
a Celeridad aguas abajo + ; celeridad aguas arriba -.
b Atenuaci�n - ; amplificaci�n +.
|
An�lisis de la atenuaci�n de la onda primaria, Fo < 2. La Figura 2 muestra la variaci�n del decremento logar�tmico δ1 para Fo < 2, en funci�n de σ*.
Se extraen las siguientes conclusiones: (1) El decremento logar�tmico δ1 es m�ximo (en valor absoluto) para un valor de σ* correspondiente al punto de inflexi�n de la curva c*r versus σ* (Fig. 1). El valor de σ* para el cual δ1 es m�ximo (en valor absoluto) disminuye al aumentar Fo; y (2) el decremento logar�tmico δ1 es m�nimo (en valor absoluto) en ambos extremos del espectro de σ*. Cuando σ* → 0, entonces δ1 → 0, lo cual corresponde al caso de la onda cinem�tica; cuando σ* → ∞, entonces δ1 → 0, lo cual corresponde al caso de la onda de gravedad.
Una conclusi�n general que se deriva de la Fig. 2, se refiere al hecho de que para Fo < 2, las ondas primarias est�n sujetas a una atenuaci�n muy fuerte en el grupo din�mico y a una atenuaci�n muy d�bil en los grupos cinem�tico y de gravedad.
|
Fig. 2 Decremento logar�tmico -δ1 de la onda primaria versus el n�mero de onda adimensional σ*
;
par�metro de curva: n�mero de Froude Fo ( Fo < 2 ).
|
|
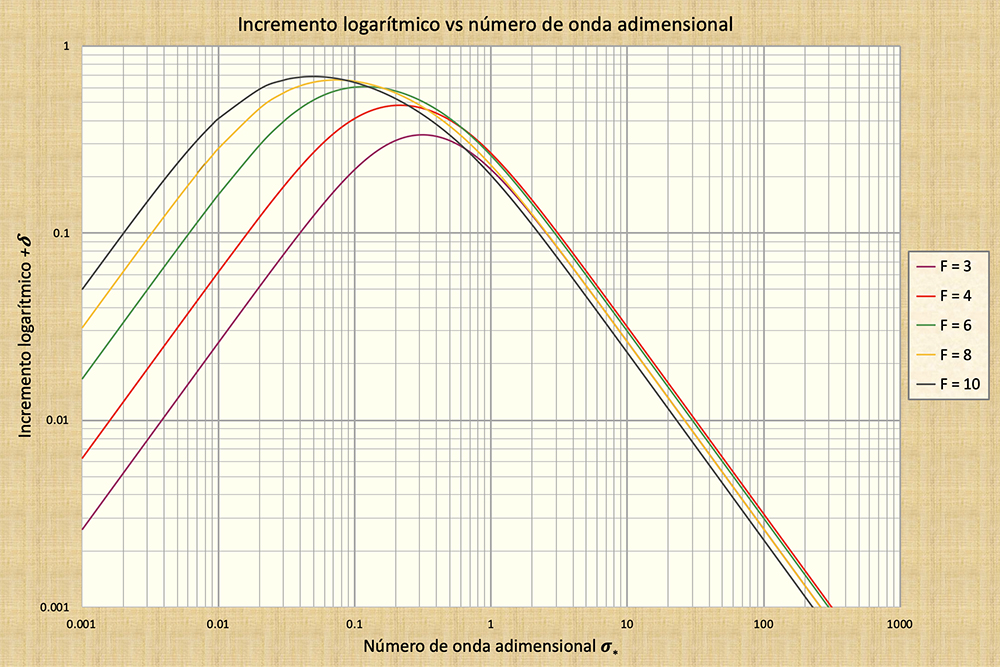
An�lisis de la amplificaci�n de la onda primaria, Fo > 2. La Figura 3 muestra la variaci�n del decremento logar�tmico δ1, para Fo > 2, en funci�n de σ*. Se extraen las siguientes conclusiones: (1) El decremento decremento/incremento logar�tmico δ1 tiene un valor m�ximo positivo en un valor de σ* correspondiente al punto de inflexi�n de la curva c*r versus σ* (Fig. 1). El valor de σ* para el cual δ1 es m�ximo disminuye al aumentar Fo; y (2) el decremento logar�tmico δ1 es m�nimo en ambos extremos del espectro σ*. Cuando σ* → 0, entonces δ1 → 0, lo cual corresponde al caso de la onda cinem�tica; cuando σ* → ∞, entonces δ1 → 0, lo cual corresponde al caso de la onda de gravedad.
Una conclusi�n general derivada de la Fig. 3 se relaciona con el hecho de que para Fo > 2, las ondas primarias est�n sujetas a una amplificaci�n muy fuerte en el grupo din�mico y a una amplificaci�n muy d�bil en los grupos cinem�tico y de gravedad.
|
Fig. 3 Incremento logar�tmico +δ1 de la onda primaria, versus el n�mero de onda adimensional σ*;
par�metro de curva: n�mero de Froude Fo ( Fo > 2 ).
|
|
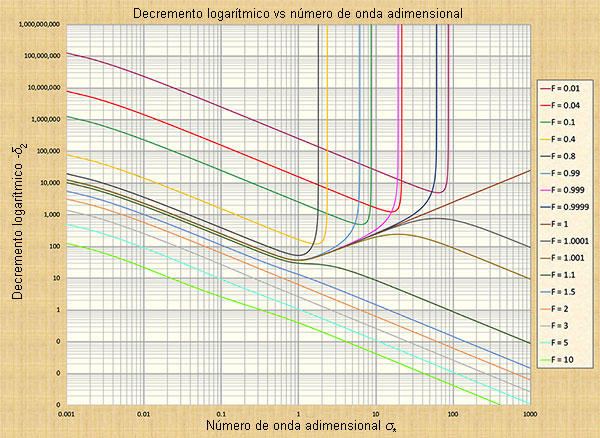
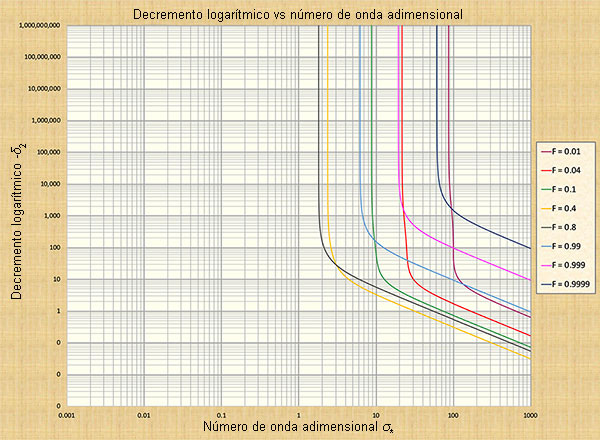
An�lisis de atenuaci�n de la onda secundaria. Las Figuras 4 (a) y 4 (b) representan la variaci�n del decremento logar�tmico δ2 para 0.01 ≤ Fo 10 en funci�n de σ*.Se extraen las siguientes conclusiones: (1) En el flujo subcr�tico, Fo < 1, la atenuaci�n de la onda secundaria es muy fuerte y la fuerza disminuye a medida que σ* aumenta en el grupo de gravedad (σ* grande); (2) en el flujo cr�tico, Fo = 1, la atenuaci�n de la onda secundaria es muy fuerte, con un m�nimo alrededor del centro del grupo din�mico (valor intermedio de σ*); y (3) en el flujo supercr�tico, Fo > 1 la atenuaci�n de la onda secundaria tiene el patr�n mostrado. Para Fo ≥ 2, δ2 disminuye a medida que σ* aumenta.
|
(a)
|
(b)
Fig. 4 Decremento logar�tmico - δ2 de la onda secundaria versus el n�mero de onda adimensional σ*;
par�metro de curva: n�mero de Froude Fo : (a) 0.01 ≤ Fo ≤ 10; (b) 0.01 ≤ Fo ≤ 0.999.
|
|
11. PROPAGACI�N DE LA ONDA DIN�MICA
La propagaci�n de las ondas en aguas poco profundas est� controlada por el balance de las diversas fuerzas incluidas en la ecuaci�n de movimiento. En la Ec. 2, el primer t�rmino representa la inercia local, el segundo la inercia convectiva, el tercer t�rmino la diferencia de presiones y el cuarto representa la acción conjunta de las pendientes de fricci�n y de fondo. Se pueden construir varios modelos de onda, dependiendo de cu�l de estos cuatro t�rminos se considere insignificante en comparaci�n con los t�rminos restantes.
Se ha demostrado que la propagaci�n de una onda din�mica es una funci�n de dos par�metros adimensionales: el n�mero de onda σ* y el n�mero de Froude Fo. El n�mero de onda σ* se puede interpretar como una relaci�n de dos longitudes Lo and L, en la cual L es la longitud de onda y Lo es la longitud horizontal en la que el flujo uniforme permanente desciende una altura (carga) igual a su profundidad. El cuadrado del n�mero de Froude Fo es la relaci�n entre el doble de la altura (carga) de velocidad y la profundidad de flujo, en la cual la altura (carga) de velocidad huo es:
uo2
huo = ______
2 g
| (61) |
Para Fo < 2, la celeridad de una onda din�mica que se propaga aguas abajo es mayor que la celeridad de la onda cinem�tica y menor que la celeridad de la onda de gravedad. De hecho, la celeridad de la onda cinem�tica constituye un l�mite inferior al que tiende el valor din�mico a medida que el n�mero de onda σ* disminuye. Por el contrario, la celeridad de la onda de gravedad es un l�mite superior a la celeridad de la onda din�mica a medida que aumenta el n�mero de onda σ*. Para situar esta conclusi�n en la perspectiva adecuada,
citamos aqu� el trabajo de Stoker [(8), p. 486], con respecto a las celeridades de peque�as perturbaciones y ondas progresivas:
"Lo que al parecer sucede es lo siguiente: los peque�os iniciadores de una perturbaci�n viajan con una velocidad (gd)1/2 relativa a la corriente de flujo, pero las fuerzas de resistencia act�an de tal manera que disminuyen la velocidad de la porci�n principal de la perturbaci�n, muy por debajo de los valores dados por (gd)1/2; es decir, para un valor
que corresponde a la velocidad de una onda progresiva permanente que viaja sin cambios de forma..."
|
Al revisar el trabajo de Stoker, es evidente que su referencia a una peque�a perturbaci�n es a una onda con un gran valor de σ* (onda de gravedad) y a una onda progresiva a aqu�lla con un peque�o valor de σ* (onda cinem�tica). Stoker prosigue elaborando en las limitaciones de los m�todos de enrutamiento del flujo basados �nicamente en el enfoque cinem�tico, para los casos en que los efectos din�micos no pueden ignorarse.
Para Fo ≥ 2, la celeridad de una onda din�mica que se propaga aguas abajo es menor que la celeridad de la onda cinem�tica y mayor que la celeridad de la onda de gravedad. De hecho, la celeridad de la onda cinem�tica es un l�mite superior al valor din�mico, mientras que la celeridad de la onda de gravedad es un l�mite inferior al valor din�mico.
Se puede obtener una conclusi�n significativa con respecto a la propagaci�n din�mica de ondas del resumen presentado en la Tabla 2. Para ondas primarias, Fo = 2 es el umbral que divide las tendencias de atenuaci�n (Fo < 2) y amplificaci�n (Fo > 2). Para ondas secundarias, sin embargo, Fo = 1 es el umbral que divide la propagaci�n aguas arriba (Fo < 1) o aguas abajo (Fo > 1) para ondas de gravedad. Por lo tanto, se comprueba que Fo = 2 es un valor umbral tan importante como Fo = 1 para describir la din�mica de los fen�menos de flujo en un canal abierto.
12. RESUMEN Y CONCLUSIONES
Las caracter�sticas de propagaci�n de varios tipos de ondas en aguas poco profundas, en el flujo de un canal abierto, se calculan usando la teor�a de la estabilidad lineal. Se derivan las funciones de celeridad y atenuaci�n de las ondas cinem�tica, de difusi�n, din�mica permanente, din�mica y de gravedad. Para el caso m�s general, es decir, el modelo de onda din�mica, las caracter�sticas de propagaci�n se expresan como una funci�n del n�mero de Froude del flujo uniforme permanente y el n�mero de onda adimensional correspondiente al componente no permanente.
Para el modelo din�mico, el espectro del n�mero de onda se divide en tres grupos: (1) Un grupo de gravedad, que corresponde a un n�mero de onda grande, en la cual la celeridad de la onda es la celeridad de la onda de gravedad; (2) un grupo cinem�tico, que corresponde a un n�mero de onda peque�o en el cual la celeridad de la onda es la celeridad de la onda cinem�tica; y (3) un grupo din�mico, que corresponde a los valores medios del espectro del n�mero de onda, en la cual la celeridad de la onda se encuentra entre los valores de celeridad cinem�tica y de gravedad.
Las ondas din�micas primarias se propagan aguas abajo y se aten�an para Fo < 2 y se amplifican para Fo > 2. En el umbral de Fo = 2, ondas din�micas primarias no se aten�an ni amplifican.
Para Fo ≤ 1, las ondas din�micas secundarias se propagan aguas arriba o aguas abajo, seg�n el n�mero de onda. Para Fo = 1, las ondas din�micas secundarias permanecen estacionarias o se propagan aguas abajo, dependiendo del n�mero de onda. Para Fo > 1, las ondas secundarias se propagan aguas abajo. Las ondas secundarias se aten�an en todo el espectro del n�mero de onda.
13. APLICACIONES
El an�lisis de este trabajo proporciona un marco apropiado para el estudio sistem�tico de las ondas en aguas poco profundas, en el flujo de un canal abierto. Se prev�n numerosas aplicaciones, entre las cuales las m�s importantes son:
La evaluaci�n de la precisi�n de los modelos cinem�ticos y de ondas de difusi�n, y la determinaci�n de los criterios para su aplicabilidad.
El estudio de la formaci�n de ondas de rollo (ondas pulsantes) en el flujo en canales abiertos. La presente teor�a valida el hecho observado de que las ondas de rollo se forman para Fo > 2, ya que no puede haber amplificaci�n de onda para Fo ≤ 2 (usando la fricci�n de Chezy).
La teor�a permite una comparaci�n de los diversos modelos aproximados de ondas y una evaluaci�n de sus propiedades y limitaciones.
Por �ltimo, la teor�a proporciona un tratamiento coherente de la propagaci�n de ondas en el flujo en canales abiertos. Las conclusiones podr�an ser de inter�s para ingenieros y cient�ficos que se ocupan de fen�menos de flujo no permanente en canales abiertos.
AP�NDICE I. BIBLIOGRAF�A
-
DeSaint-Venant, B. 1871. "Theorie du Mouvement Non-permanent des Eaux avec Application aux Crues des Rivieris et I' Introduction des Varies dans leur Lit," Competes Rendus Hebdomadaires des Seances de l'Academie des Science, Paris, France, Vol. 73, 148-154.
-
Henderson, F. M. 1966, Open Channel Flow, The MacMillan Co., New York, N.Y.
-
Lagrange, I. L. "Mémoire sur la Théorie du Mouvement des Fluides," Bulletin de la Classe des Sciences Academie Royal de Belique, No. 1783, 151-198.
-
Liggett, J. A. 1975. "Basic Equations of Unsteady Flow," Unsteady Flow in Open Channels, K. Mahmood and V. Yevjevich, ed., Vol. 1, Water Resources Publications, Fort Collins, Colo.
-
Lighthill, M. J. and G. D. Whitham. 1955. "On Kinematic Waves I, Flood Movement in Long Rivers," Proceedings of the Royal Society of London, Vol. A229, May, 281-316.
-
Lin, C. C. 1966.The Theory of Hydrodynamic Stability, 1st ed., The Cambridge University Press, London, England.
-
Ponce, V. M., and K. Mahmood. 1976. "Meandering Thalwegs in Straight Alluvial Channels," Proceedings of the 3rd Annual Symposium, ASCE, Waterways, Harbors, and Coastal Engineering Division, Vol. 2, Aug., 1418-1441.
-
Stoker, J. J. 1957. Water Waves, the Mathematical Theory with Applications, Wiley Interscience Publishers, Inc., New York, N.Y.
-
Woolhiser, D. A., and J. A. Liggett. 1967. "Unsteady One-Dimensional Flow over a Plane-The Rising Hydrograph," Water Resources Research, Vol. 3, No. 3, Third Quarter, 753-771.
-
Wylie, C. R. 1966. Advanced Engineering Mathematics, 3rd ed., McGraw-Hill Book Co., New York, N.Y.
AP�NDICE II. NOTACI�N
En este documento se utilizan los siguientes s�mbolos:
A = par�metro, definido por la Ec. 39;
a = n�mero entero;
B = par�metro, definido por la Ec. 40;
C = par�metro, definido por la Ec. 41;
Cf = coeficiente de Chezy;
D = par�metro, definido por la Ec. 50;
d = profundidad de flujo;
E = par�metro, definido por la Ec. 51;
Fo = n�mero de Froude de flujo uniforme permanente;
f = factor de fricci�n, definido por la Ec. 7;
g = aceleraci�n de la gravedad;
hu = carga de velocidad;
k = n�mero entero;
L = longitud de onda;
Lo = longitud horizontal en cual el flujo permanente cae una altura igual a su profundidad;
l = n�mero entero;
p = n�mero entero;
Sf = pendiente de fricci�n;
So = pendiente de fondo;
T = per�odo de onda;
u = velocidad media;
β*I = factor de amplitud de propagaci�n;
β*R = frecuencia adimensional;
γ = peso unitario del agua;
δ = decremento logar�tmico;
ζ = un tipo de n�mero de flujo cinem�tico, seg�n lo definido por la Ec. 37;
θ = par�metro, definido por la Ec. 43;
σ* = n�mero de onda adimensional;
τ = esfuerzo cortante de fondo; y
∞ = infinito.
Sub�ndices
d = onda difusiva;
g = onda de gravedad;
I = imaginario;
k = onda cinem�tica;
o = flujo uniforme permanente;
R = real;
r = relativo al flujo principal;
s = onda din�mica permanente;
1 = onda din�mica primaria; y
2 = onda din�mica secundaria.
Super�ndices
' = variable de perturbaci�n; y
* = funci�n adimensional.
|
|
|