1. EVAPORATION

1.01
Evaporation is the process by which water accumulated on the land surface is converted into vapor state and returned to the atmosphere.

1.02
Evaporation occurs at the evaporation surface, the contact between water body and overlying air.

1.03
Evaporation refers to the net rate of water loss from the water body to the atmosphere.

1.04
The evaporation rate, in mm/day or inches per day, is a function of the following meteorological variables:

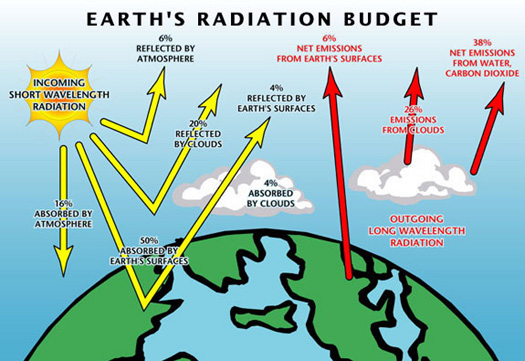
• Net solar radiation

• Saturation vapor pressure

• Vapor pressure of the overlying air

• Air and water temperatures

• Wind velocity

• Atmospheric pressure

1.05
Evaporation rates vary with the climate.

1.08

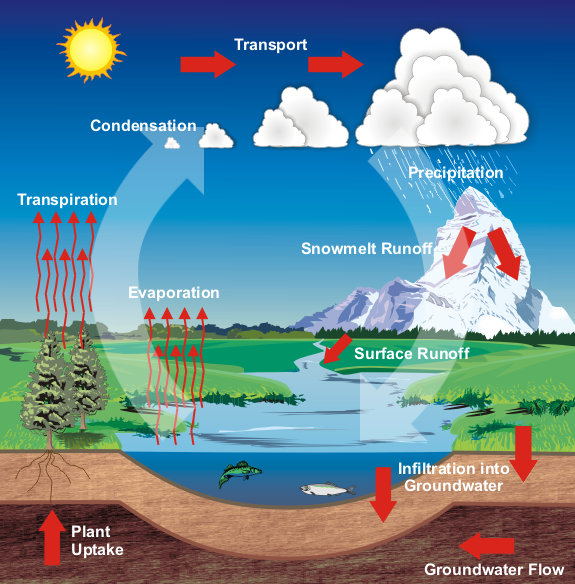
Salton Sea at Bombay Beach, California.

• Water-budget method

• Energy-budget method

• Mass-transfer methods

2.01
The water budget method assumes that all relevant water-transport phases can be evaluated for a period of time Δt, and expressed in terms of volumes.

2.02
In this formula:

• E is the volume evaporated from the reservoir

• P is the precipitation falling directly into the reservoir

• Q is the surface runoff inflow into the reservoir

• O is the outflow from the reservoir

• I is the net infiltration from the reservoir into the ground

• ΔS is the change in stored volume.

2.03

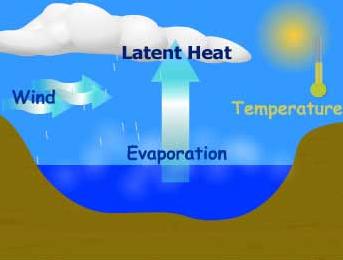
2.04

Precipitation P is readily measured.

2.05

Inflow Q and outflow O can be obtained by integrating flow records.

2.06

Net infiltration I can be evaluated indirectly, by monitoring changes in groundwater level in nearby wells.

2.07

The change in stored volume ΔS is determined by means of water stage recorders.

3. ENERGY-BUDGET METHOD

3.01
The energy budget method is based on a balance of energy exchanges.

3.02

The heat of vaporization, that is, the amount of heat required to convert one gram of water into vapor, varies with the temperature.

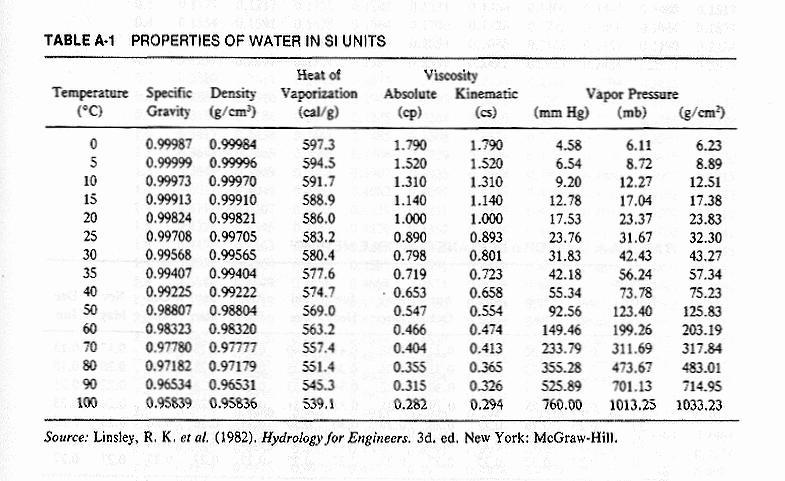
3.03

At 20^oC, the heat of vaporization is equal to 568 calories.

3.04

Heat must be supplied for evaporation to take place.

3.05

Radiation is the emission of energy in the form of electromagnetic waves.

3.06

Solar radiation received at the Earth's surface is a major component of the energy balance.

3.07

Solar radiation reaches the outer surface of the atmosphere at a nearly constant flux of 1.94 cal/cm²/min.

3.08

NASA Goddard Space Flight Center

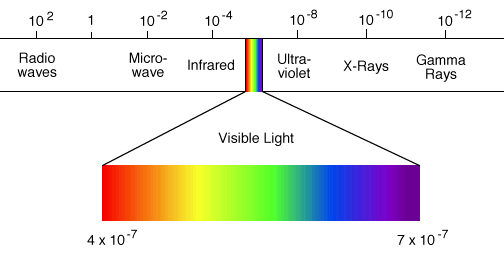
3.09

Nearly all of this radiation is of wavelengths in the range 0.3-3.0 micrometers, with about half in the visible range, between 0.4 and 0.7 micrometers.

3.10

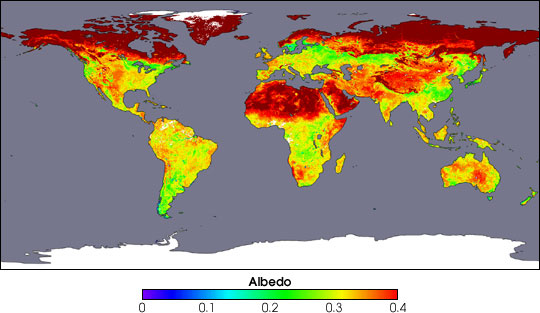
3.11

The Earth also emits radiation, but this terrestrial radiation is of much lower intensity and greater wavelength than solar radiation.

3.12
Terrestrial radiation is in the range of 3 to 50 micrometers.

3.13

It is customary to refer to solar radiation as short-wave radiation, and to terrestrial radiation as long-wave radiation.

3.14

The fraction of original solar radiation that reaches the Earth's surface is called direct solar radiation.

3.15

The fraction that reaches the ground after reflection and scattering is called sky radiation.

3.16

The sum of direct solar and sky radiation is called global radiation.

3.17

Albedo is the reflectivity coefficient of a surface toward shortwave radiation.

3.18

Albedo varies with color, roughness, and inclination of the surface.

3.19

Values of albedo range from 0.03-0.10 for water, 0.10-0.30 for vegetated areas, 0.05-0.40 for bare soil, 0.30-0.60 for sand dunes, and 0.50-0.95 for snow-covered areas.

3.20

NASA

3.21

In addition to short wave radiation, there is also long-wave radiation.

3.22

The Earth emits long-wave radiation, part of which is absorbed and reflected back by the atmosphere.

3.23

NASA

3.24

The difference between outgoing and incoming fluxes is called long-wave radiation loss.

3.25

At night, long-wave radiation predominates.

3.26

Net radiation is equal to the net short-wave radiation minus the long-wave radiation loss.

3.27
For a water body, a balance of incoming and outgoing radiation leads to:

3.28

3.29
In this formula:

• Q_s is the global radiation

• A is the albedo

• Q_b is the long-wave radiation loss

• Q_a is the energy advected into the waterbody by streams, rain, snow, etc.

• Q_h is the sensible heat transfer from waterbody to atmosphere by convection and conduction

• Q_e is the evaporative or latent heat transfer

• Q_t is the increase in energy stored in the water body

3.30
The Bowen ratio is defined as the ratio of sensible heat to latent heat.

3.31

3.32

3.33
Ira Sprague Bowen, 1998-1973, was a prominent astrophysicist that first defined the ratio between terrestrial heat fluxes.

3.34
In terms of climatic variables, the Bowen ratio is:

3.35

3.36
in which:

• gamma is a pychrometric constant, which is approximated as 0.66 millibars per degree Celsius

• T_s is the water surface temperature, in degree Celsius

• T_a is the overlying air temperature, in degree Celsius

• e_s is the saturation vapor pressure at the water surface temperature, in millibars

• e_a is the partial vapor pressure of the overlying air, in millibars

• p is the atmospheric pressure, in millibars.

• 1000 is a constant in millibars.

3.37
The relation between evaporative heat and evaporation rate is:

3.38

3.39
in which

• Q_e is the evaporative heat in cal/cm²/day,

• rho is the density of water in gr/cm³,

• lambda is the heat of vaporization in cal/gr, and

• E is the evaporation rate in cm/day.

3.40
This relation allows the conversion of evaporative heat to evaporation rate, and vice versa.

3.41
The balance of incoming and outgoing energy leads to an expression for evaporation rate:

3.42

3.43
The quantities Q_s and Q_b can be measured with radiometers.

3.44
The advected energy Q_a and increase in energy stored in the water body Q_t can be assessed by periodic measurements of volume and temperature.

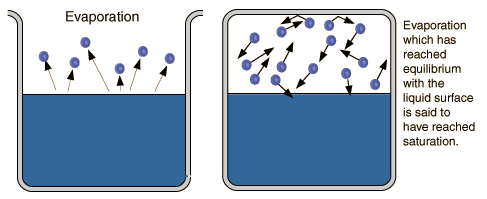
4.01

Evaporation rates are dependent on the temperature of the water surface and the prevailing atmospheric pressure.

4.02

Higher water temperatures result in higher evaporation rates.

4.03

Higher atmospheric pressure results in lower evaporation rates.

4.04

Temperature has a larger effect on evaporation than atmospheric pressure.

4.05

Evaporation rates are a function of the difference between the saturation vapor pressure at the water surface temperature e_s and the partial vapor pressure of the overlying air e_a.

4.06

The saturation vapor pressure is the equilibrium vapor pressure in a closed container.

4.07

The partial vapor pressure is the nonsaturation vapor pressure in an open container.

4.08

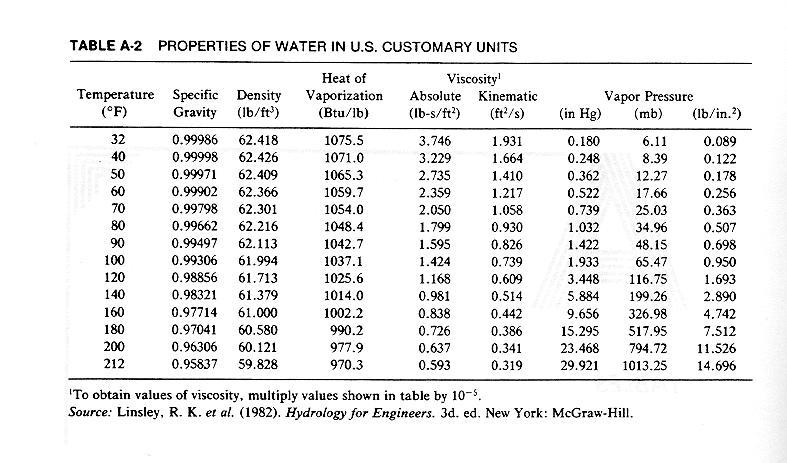
4.09

The saturation vapor pressure is a function of temperature.

4.10

4.11

The partial vapor pressure of the air e_a can be obtained by multiplying the saturation vapor pressure at the overlying air temperature e_o by the relative humidity of the air φ in percentage, and dividing by 100.

4.12

4.13

As the process of mass transfer continues, the lowest layer of the atmosphere eventually becomes saturated, and net evaporation reduces to zero and can become negative, that is, it can condensate.

4.14

The wind carries away water molecules and helps continuous evaporation.

4.15

The Dalton formula for evaporation considers the vapor pressure difference and wind effects.

4.16

4.17
in which f(u) is a certain wind function, and

(e_s - e_a) is the vapor pressure difference.

4.18
John Dalton published a paper in 1802 which was one of the major events in the development of evaporation theory.

4.19

4.20

The Dalton formula can also be expressed in terms of e_o, the saturation vapor pressure at the air temperature, instead of e_s, at the water surface temperature.

4.21

4.22
This formula is particularly useful when the water surface temperature is unavailable, or when it can be assumed that it is close enough to the overlying air temperature.

4.23

In terms of saturation vapor pressure at the overlying air temperature e_o and percent relative humidity φ, the Dalton formula is

4.24

5. THE PENMAN METHOD

5.01
In 1948, Howard Penman combined the energy budget and mass-transfer methods to obtain a combination formula for evaporation rate.

5.02

(1909-1984)

5.03
Penman assumed an approximate energy balance, neglecting Q_a, the energy advected into the waterbody by streams, rain, and snow, and Q_t, the increase in energy stored in the water body, which led to

5.04

5.05
The left-hand side of this equation is the net radiation Q_n.

5.06

5.07
In terms of the Bowen ratio, the net radiation is:

5.08

5.09
In terms of evaporation units, this equation converts to:

5.10

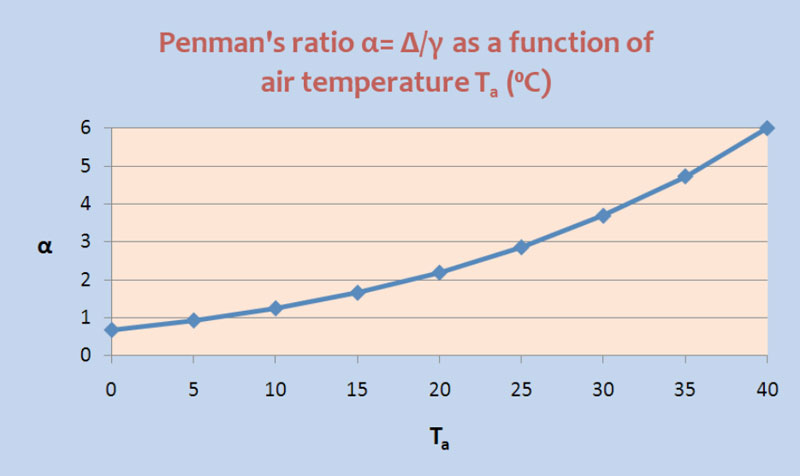
5.11

in which E_n is the net radiation in evaporation rate units, and E is the evaporation rate.

5.12
The atmospheric pressure at sea level is 1013.2 millibars.

5.13
For p = 1000 mb, which is close to atmospheric pressure at sea level, the Bowen ratio simplifies to:

5.14

5.15
Penman defined a saturation vapor pressure gradient Δ between water and air temperatures as follows:

5.16

5.17
Furthermore, Penman assumed that the ratio of mass-transfer evaporation rate E_a to evaporation rate E is:

5.18

5.19
Combining these four equations, Penman developed a formula for evaporation rate E:

5.20

5.21
Defining α = Δ / γ, the Penman equation simplifies to:

5.22

5.23
The quantity alpha is a function solely of the air temperature.

5.24

5.25
Thus, evaporation rate by Penman's method is a function of solar radiation, air temperature, relative humidity, and a wind function.

5.26
The latter is a function of the wind velocity.

Narrator: Dr. Victor M. Ponce

Music: Fernando Oñate

Editor: Flor Pérez

Photo Credits: Google

Copyright © 2010

Visualab Productions

All rights reserved