|
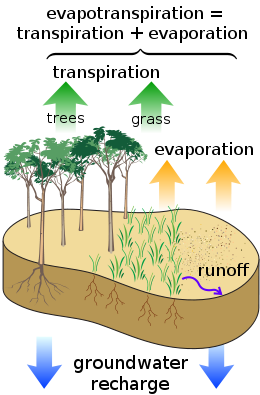
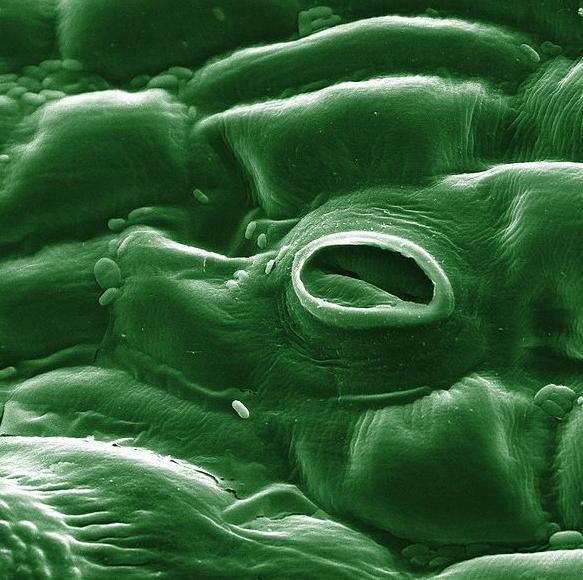
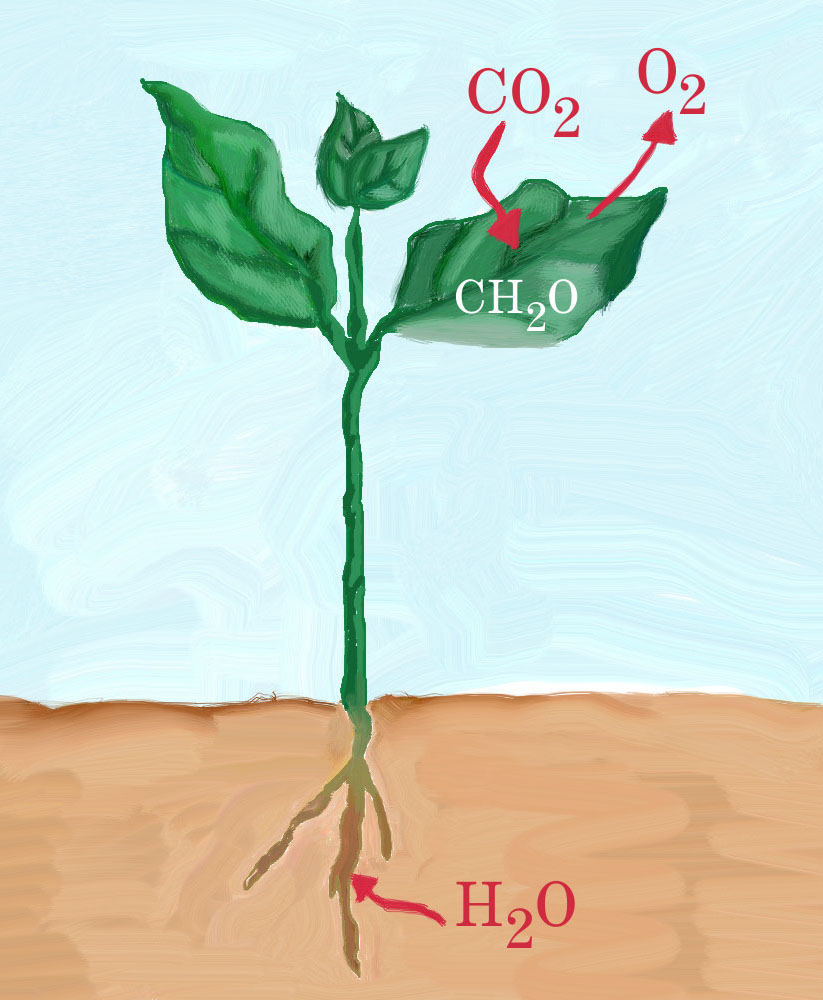
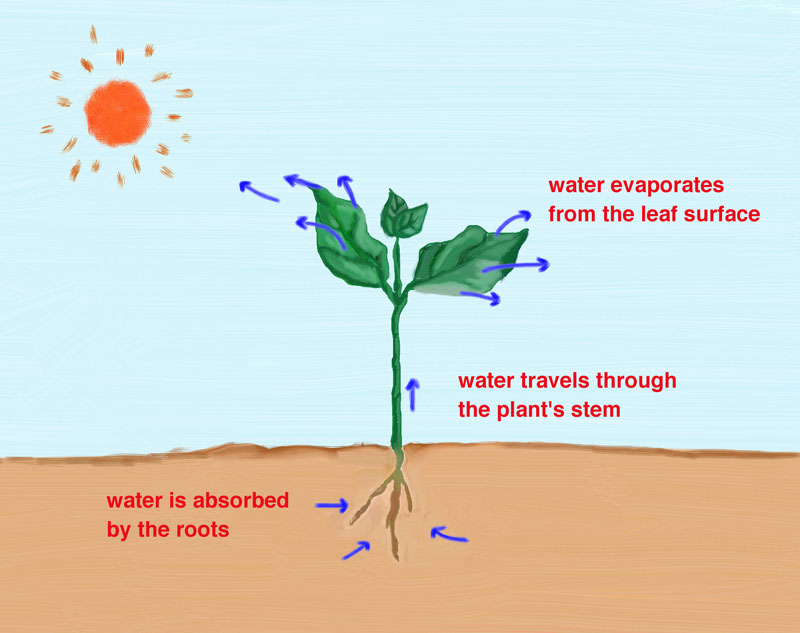
ENGINEERING HYDROLOGY 024 : EVAPOTRANSPIRATION
1.01 1.02 1.03
1.04 1.05 1.06 1.07 1.08
1.09 1.10
1.11 1.12 1.13 1.14
1.15 1.16 1.17 1.18 1.19 1.20 1.21 1.22 1.23 • Temperature models • Radiation models • Combination models • Pan-evaporation models.
2.01 2.02 2.03 2.04
2.05 F = evapotranspiration, in inches per month P = ratio of total daytime hours for a given month to the total daytime hours in a year T = temperature, in degrees Farenheit. 2.06
2.07 2.08
2.09 in which f = consumptive use factor, in mm/day p = ratio of mean daily daytime hours for a given month to total daytime hours in the year, in percentage, a function of latitude. t = mean daily temperature, in degrees Celsius 2.10 The average daily value of p, applicable along the equator, is p = 100 (0.08333 / 30) = 0.27778
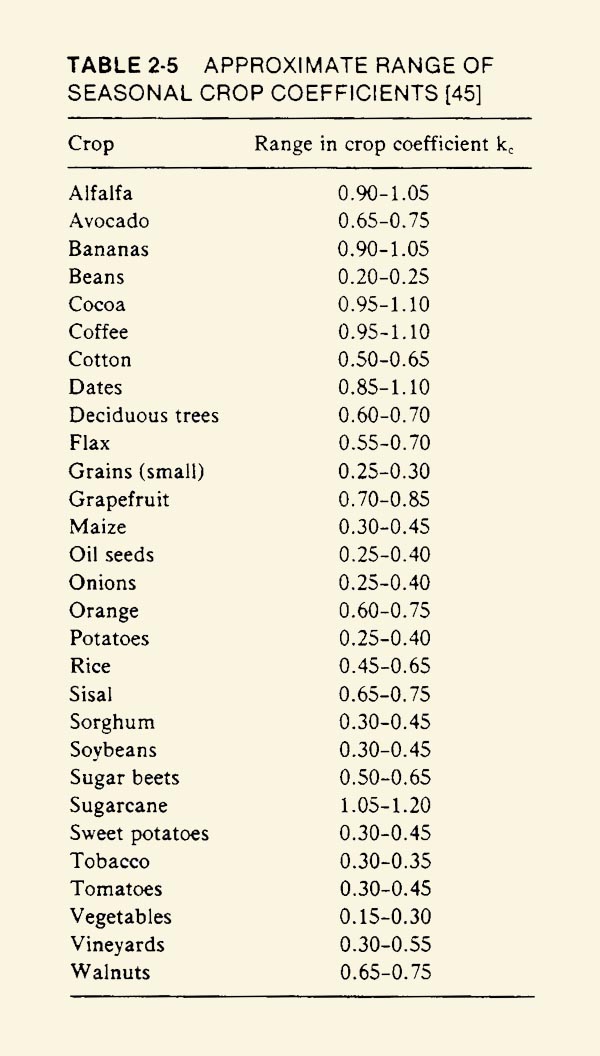
2.11 The consumptive water requirement is equal to the product of the consumptive use factor f times an empirical crop coefficient kc, which varies as shown in the following table. 2.12
2.13 Doorenbos and Pruitt have proposed a modification of the Blaney-Criddle formula, which has been widely accepted:
2.14
2.15 in which ETo is the reference crop evapotranspiration, and a and b are constants that vary with
2.16
2.17
2.18 The consumptive water requirement ETc is 2.19
2.20 The Thornthwaite method is also widely used to estimate potential evapotranspiration. 2.21 The method is popular because it is based only on temperature, which is widely available. 2.22 The method is based on an annual temperature efficiency index J, defined as the sum of 12 monthly values of heat index I. 2.23 Each monthly index I is a function of mean monthly temperature T, in degrees Celsius: 2.24
2.25 Potential evapotranspiration at zero latitude in cm/month is calculated by the following formula: 2.26
2.27
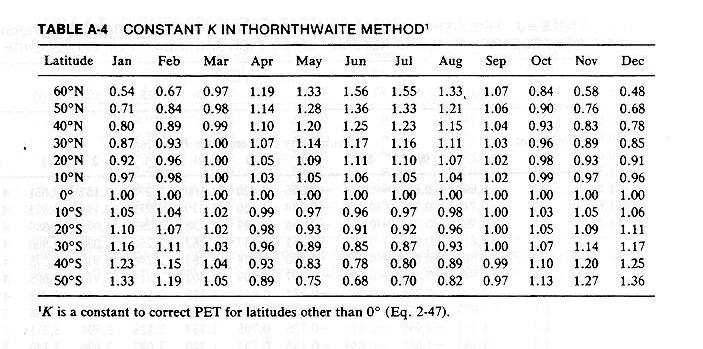
2.28 At latitudes other than zero, potential evapotranspiration is calculated by the following formula:
2.29
2.30 K is a constant for each month of the year, varying as a function of latitude.
2.31
3.01 Priestley and Taylor proposed that potential evapotranspiration be taken as the radiation part of the Penman equation, multiplied by an empirical constant.
3.02
3.03 Defining α = Δ / γ, the Priestley-Taylor equation simplifies to:
3.04
3.05
The relation between evaporative heat and evaporation rate is: 3.06
3.07 in which ρ is the density of water, and &lambda is the heat of vaporization.
3.08
3.09
3.10 The constant 1.26 may vary with climatic conditions.
3.11
4.01 The original Penman model provided an estimate of evaporation from a free surface.
4.02 Experimental crop coefficients were used to convert evaporation to evapotranspiration.
4.03 These coefficients, 0.6 in the winter and 0.8 in the summer, were intended to multiply the evaporation to get the evapotranspiration.
4.04 Other studies have suggested that free-water-surface evaporation and evapotranspiration are nearly the same.
4.05 Energy-budget and mass-transfer components may compensate themselves to make evaporation and evapotranspiration nearly equal.
5.01 Pan evaporation models are also used in evapotranspiration studies.
5.02 The most common evaporation pan is the NWS Class A pan.
5.03 The pan is circular, 122 cm in diameter and 25.4 cm deep, made of galvanized iron.
5.04
5.05
NWS Class A evaporation pan 5.06 The basic pan evaporation formula is the following:
5.07
5.08 in which PET is the potential evapotranspiration, Ep is the pan evaporation and kp is a pan coefficient, varying between 0.35 and 0.85, depending on pan exposure, relative humidity, and wind speed. Narrator: Dr. Victor M. Ponce Music: Fernando Oñate Editor: Flor Pérez Photo Credits: Google
Copyright © 2010 Visualab Productions All rights reserved
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||