1. SMALL CATCHMENTS

1.1
Catchments possessing some or all of the following properties are small in a hydrologic sense:

1. Rainfall can be assumed to be uniformly distributed in time,

2. Rainfall can be assumed to be uniformly distributed in space,

3. Storm duration usually exceeds the time of concentration,

4. Runoff is primarily by overland flow rather than by channel flow, and

5. Channel storage processes are negligible, that is, channels are either steep or short.

1.2
The runoff response of small catchments can be described with relatively simple parametric methods.

1.3
In certain cases, a more complex overland flow analysis may be warranted.

1.4
The upper limit of a small catchment is somewhat arbitrary.

1.5
Time of concentration and catchment area are used to describe the upper limit.

1.6
A time of concentration substantially less than 1 hour describes a small catchment.

1.7
More commonly, a catchment less than 2.5 km², or 1 square mile, is considered small in a hydrologic sense.

1.8

Small catchment, Moyan watershed, Lambayeque, Peru.

2. RATIONAL METHOD

2.1
The rational method is a widely used method for the calculation of peak flows from small catchments.

2.2
It was originally proposed by Emil Kuichling in 1889.

2.3
It has particular application in urban storm drainage design.

Urban drainage inlet (University of South Queensland, Australia).

2.4
The popularity of the rational method is attributed to its simplicity, although reasonable care is necessary in order to use it correctly.

2.5
The rational method takes into account the following hydrologic characteristics or processes:

• Rainfall intensity

• Rainfall duration

• Rainfall frequency

• Catchment area

• Hydrologic abstractions

• Runoff concentration

• Runoff diffusion

2.6
In general, the rational method provides only a peak discharge, although in the absence of runoff diffusion it also gives an isosceles-triangle-shaped hydrograph.

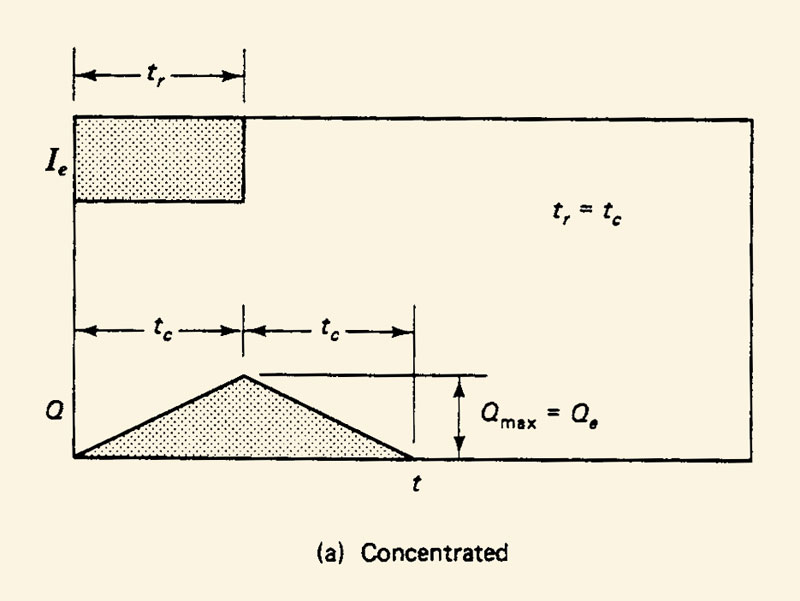
Hydrograph produced by the rational method.

2.7
The peak discharge is the product of:

• Runoff coefficient,

• Rainfall intensity, and

• Catchment area,

2.8
All processes are lumped into these three parameters.

2.9
Rainfall intensity contains information on rainfall duration and frequency.

2.10
Rainfall duration is made equal to the time of concentration, that is, concentrated catchment flow is assumed.

2.11
The runoff coefficient accounts for hydrologic abstractions and runoff diffusion, and may also indirectly account for frequency.

2.12
All major processes are embodied in the rational method.

2.13
The rational method does not take into account the following processes:

• The presence of spatial or temporal variations in either total or effective rainfall,

• A time of concentration much greater than rainfall duration,

• A significant portion of the runoff occurring in the form of streamflow.

• The catchment's antecedent moisture condition, although this condition may be implicitly incorporated into the runoff coefficient.

2.14
The applicability of the rational method is restricted to small catchments.

2.15
The assumption of constant rainfall in time and space is strictly valid only for small catchments.

2.16
For small catchments, storm duration usually exceeds the time of concentration.

2.17
For small catchments, overland flow prevails over streamflow.

2.18
In practice, the upper limit for a small catchment is in the range 1.3 to 2.5 km², or 0.5 to 1 square miles.

2.19

Highway culvert, La Paz, Baja California Sur, Mexico.

2.20
Some counties place the upper limit of applicability of the rational method as little as 160 acres, that is, 0.25 square miles.

2.21
The rational formula is:

2.22

2.23
where

Q_p = peak discharge,

C = runoff coefficient, varying between 0 and 1,

I = rainfall intensity, and

A = catchment area.

2.24
The runoff coefficient C is the ratio of effective rainfall intensity to total rainfall intensity.

2.25
Therefore, the rational formula is a statement of runoff concentration:

2.26

2.27
where

I_e = effective rainfall intensity, and

Q_p = peak flow, equilibrium, or maximum flow.

2.28
For rainfall intensity in millimeters per hour, area in square kilometers, and peak discharge in cubic meters per second:

2.29

2.30
For rainfall in millimeters per hour, area in hectares, and peak discharge in Liters per second:

2.31

2.32
For rainfall in inches per hour, area in acres, and peak discharge in cubic feet per second:

2.33

2.34
The unit conversion coefficient 1.008 is usually neglected on practical grounds.

2.35
The rational method can be solved online with rational.sdsu.edu

3. METHODOLOGY

3.1
The assumptions of the rational method dictate that the catchment be small.

3.2
The catchment area is determined by suitable means.

3.3
The time of concentration is determined:

• Using an empirical formula, or

• For developed areas, assuming a flow velocity based on hydraulic principles and computing the travel time.

3.4

Hillside urban development, Tijuana, Baja California, Mexico.

3.5
The procedures involves the assumption of flow levels, channel shape, and friction coefficients.

3.6
The travel time and, therefore, the time of concentration, is a complex function of flow level.

3.7

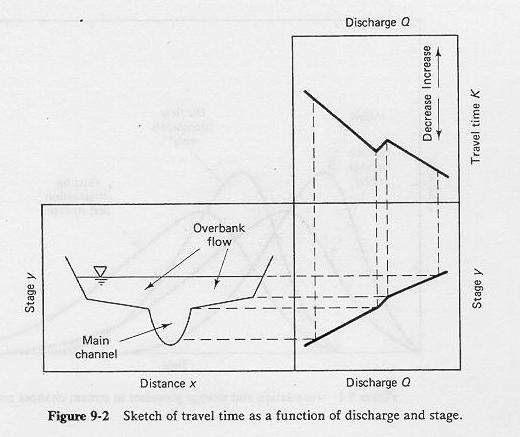
Sketch of travel time as a function of discharge and stage in a stream or channel.

3.8
The assumption of concentrated catchment flow requires that the design storm duration be equal to the time of concentration.

3.9
A rainfall frequency is chosen, to vary from 5 to 10 yr for storm sewers in residencial areas, 10 to 50 yr for commercial areas, and 50 to 100 yr for regional flood protection works.

3.10
Rainfall intensities are higher for shorter durations.

3.11
Rainfall intensities are higher for longer frequencies.

3.12

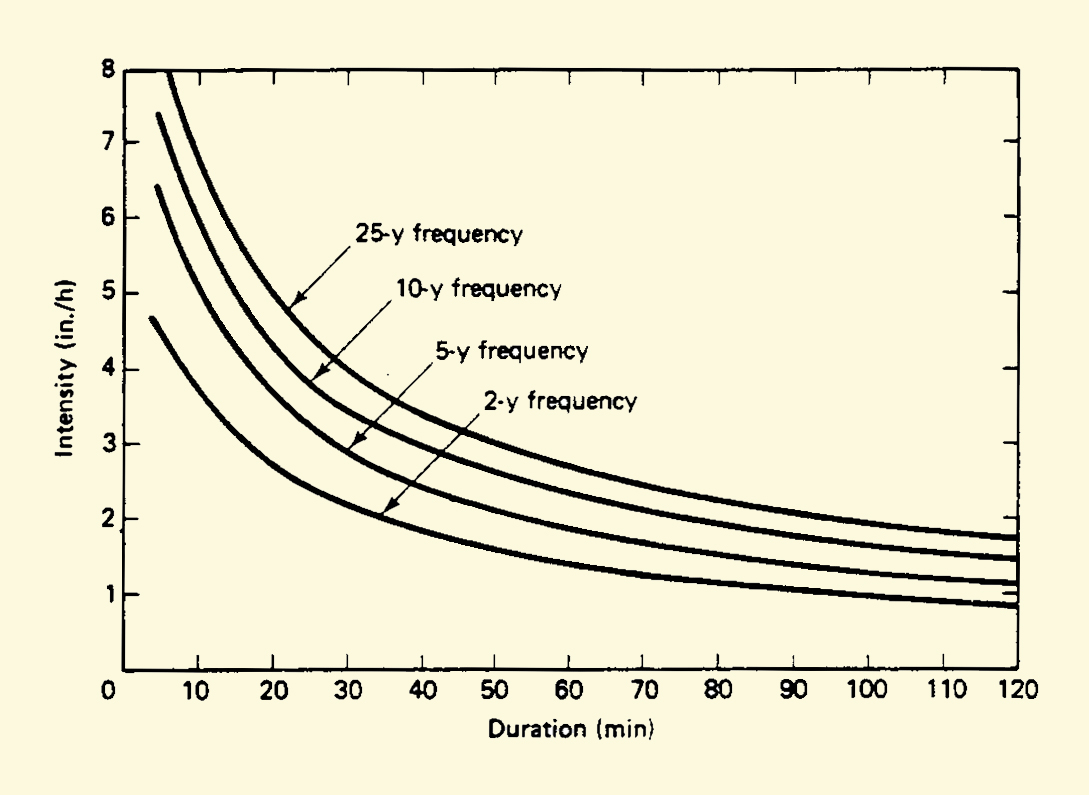
An intensity-duration-frequency curve.

3.13
The frequency of rainfall and runoff events may not be the same.

3.14
In practice, runoff coefficients are adjusted upward to reflect postulated decreases in runoff frequency.

3.15
The rainfall intensity is obtained from an applicable intensity-duration-frequency curve.

3.16
The runoff coefficient applicable to 5-yr and 10-yr frequency is obtained from an appropriate table or from local experience.

3.17

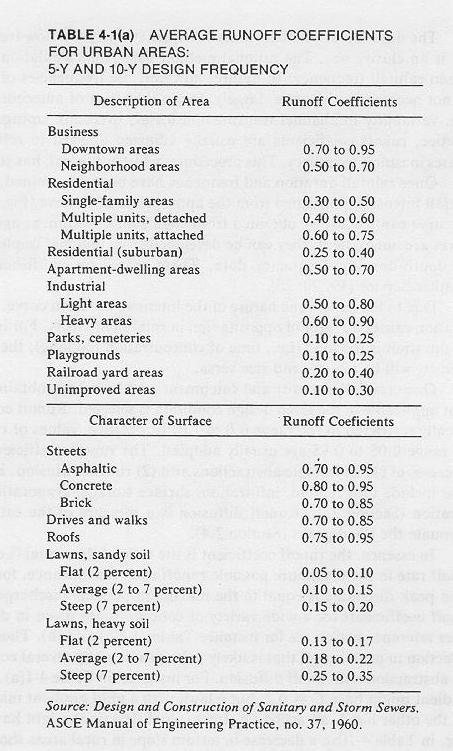
3.18
In practice, runoff coefficients vary with rainfall intensity and frequency.

3.19
An example of the variation of runoff coefficient with rainfall intensity is shown here.......

3.20

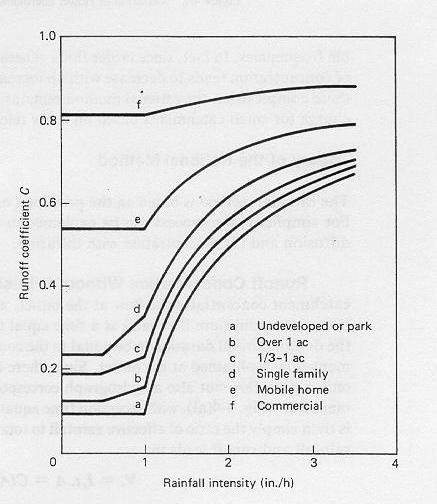
3.21
An example of the variation of runoff coefficient with rainfall frequency is shown here.......

3.22

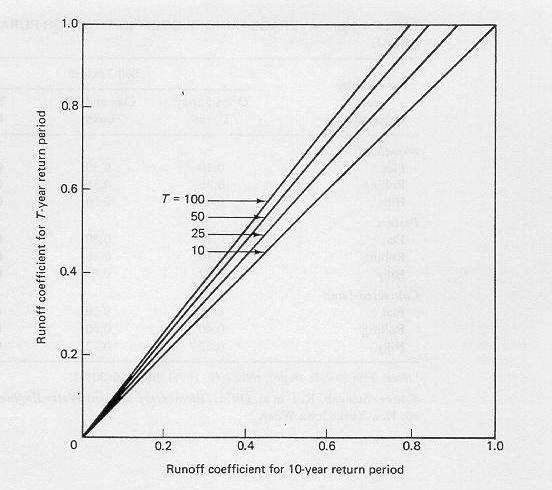
Narrator: Victor M. Ponce

Music: Fernando Oñate

Editor: Flor Pérez

Image Credits: Google

Copyright © 2010

Visualab Productions

All rights reserved