1. OVERLAND FLOW

1.01
Overland flow is surface runoff that occurs in the form of sheet flow on the land surface, without concentrating in clearly defined channels.

1.02
Overland flow is the first manifestation of surface runoff.

1.03
Overland flow uses conceptual and deterministic methods to describe surface runoff in overland flow planes.

1.04

Overland flow in the Lower Chaco, Paraguay.

1.05
In overland flow applications, effective rainfall is referred to as rainfall excess.

1.06
Overland flow can account for runoff concentration and diffusion, producing a hydrograph that reflects the combined effect of these two properties.

1.07
Rainfall can be allowed to vary in time and space if necessary.

1.08
An overland flow calculation is more complex that the rational method.

1.09
Overland flow solves the problem of hydrograph shape very well.

1.10
For single storms, the peak flow calculated by overland flow is the same as that calculated by the rational method.

1.11
In a modeling framework, with many overland flow modules, the calculated peak flow has more detail than that of the rational method.

1.12

Hillslopes of the Moyan watershed, Lambayeque, Peru.

1.13
Overland flow applies to small catchments, but may also be applied to midsize catchments.

1.14
Small modules will usually retain the topographic details.

1.15

Overland flow, Japani hillslopes, Lima, Peru.

1.16
Larger modules may lose topographic detail, masking the distributed character of overland flow.

1.17
However, in regional swamps, extensive areas may be subject to uniform overland flow.

1.18
This is the case of the Everglades, in South Florida.

1.19

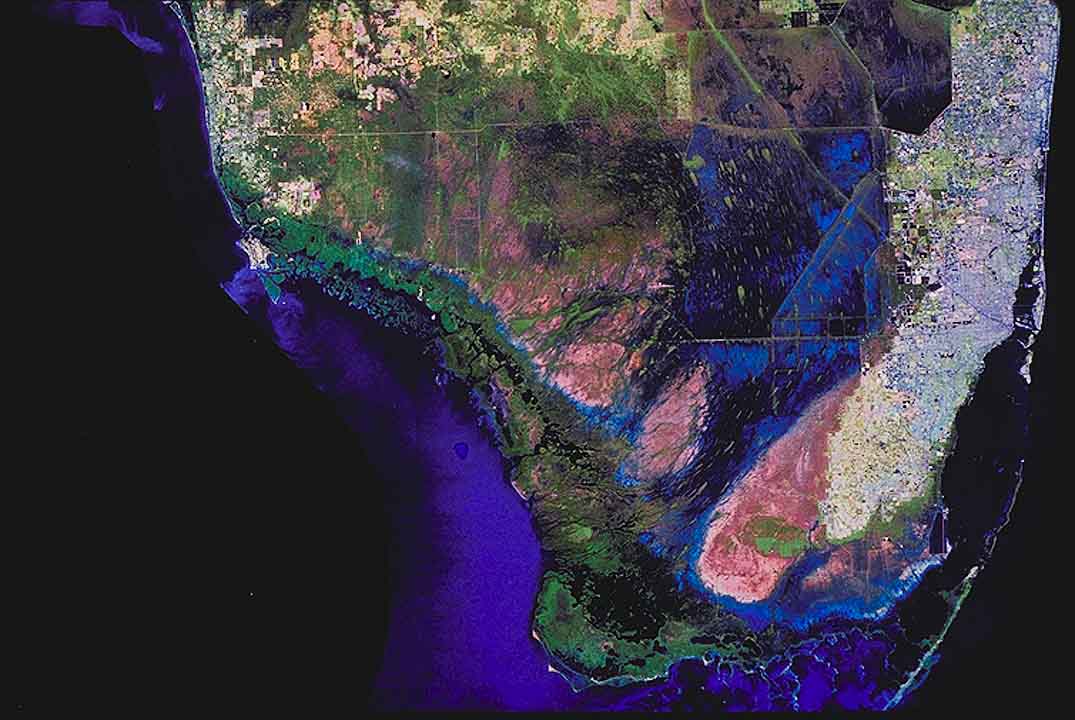
Overland flow in the Everglades, South Florida.

1.20

In practice, overland flow is often used in a GIS context.

2. EQUATIONS

2.01
The equation of mass conservation in a control volume is:

2.02

2.03
where Q = discharge, and A = flow area.

2.04
The inclusion of sources and sinks leads to:

2.05

2.06
where q_L = lateral inflow, per unit of channel length.

2.07
On the overland flow plane, the equation of mass conservation, per unit of plane width, is:

2.08

2.09
where

q = discharge per unit of plane width,

h = flow depth, and

i = rainfall excess.

2.10
Flow over the plane can be described as follows:

2.11

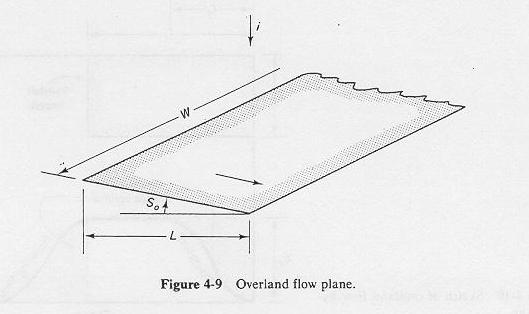
Definition sketch for the overland flow plane.

2.12
1. As excess rainfall begins, water accumulates on the plane surface and begins to flow out of the plane at its lower end.

2.13
2. Flow at the outlet increases gradually from zero, while the total volume of water stored over the plane also increases gradually.

2.14
3. If rainfall excess continues, both outflow and total volume of water stored over the plane reach a constant value.

2.15
4. After that point, outflow and storage volume remain constant and equal to the equilibrium value until rainfall excess ceases.

2.16
5. After excess rainfall ceases, outflow begins to draw water from storage, gradually decreasing while depleting the storage volume.

2.17
6. Eventually, outflow returns to zero as the storage volume is completely drained.

2.18

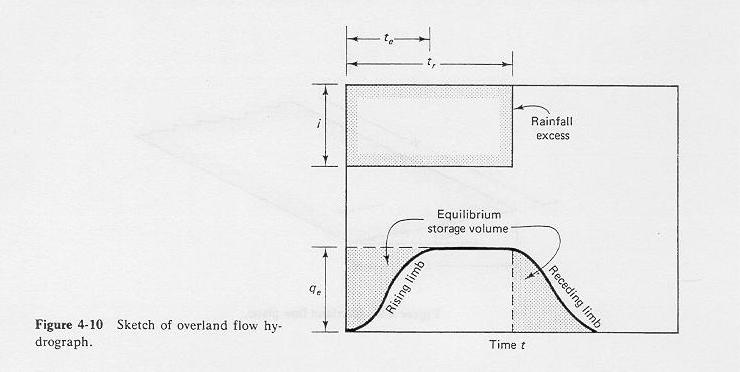
Sketch of overland flow hydrograph.

2.19
At equilibrium state, the outflow must equal the inflow. Therefore:

2.20

2.21
in which:

q_e = equilibrium outflow in Liters per second per meter

i = rainfall excess in millimeters per hour

L = plane length in meters.

2.22
This equation is a statement of runoff concentration applied to overland flow.

2.23
The equilibrium storage volume is the area above the rising limb and below a line q = q_e.

2.24
As a first approximation, the equilibrium storage volume can be assumed to be equal to:

2.25

2.26
in which:

S_e= equilibrium storage volume in Liters per meter

q_e= equilibrium outflow in Liters per second per meter

t_e = time to equilibrium in seconds.

2.27
In practice, surface irregularities cause the equilibrium state to be approached asymptotically, and the actual time to equilibrium is not clearly defined.

2.28
A value of t corresponding to q = 0.98 q_e may be taken as a practical approximation of the time to equilibrium.

2.29
The equation of water continuity is:

2.30

2.31
in which

q = discharge per unit of width,

u = mean velocity, and

h = flow depth.

2.32
Since q = uh, the equation of conservation of mass, or equation of continuity, can be expressed as follows:

2.33

2.34
A statement of conservation of momentum leads to the equation of motion:

2.35

2.36
where

S_f = friction slope,

S_o = bottom slope, and

g = gravitational acceleration.

2.37
The equations of continuity and motion are a set of nonlinear partial differential equations, for which a complete analytical solution is not available.

2.38
In practice, inertia usually plays a minor role in overland flow.

2.39
Thus, the neglect of inertia is justified on practical grounds.

2.40
Overland flow is solved using either of the following three approximations:

2.41

1. The storage concept.

2. The kinematic wave technique.

3. The diffusion wave technique.

2.42
The storage concept is conceptual.

2.43
The kinematic and diffusion wave techniques are deterministic.

2.44
They are based on the equation of continuity and simplifications of the equation of motion.

2.45

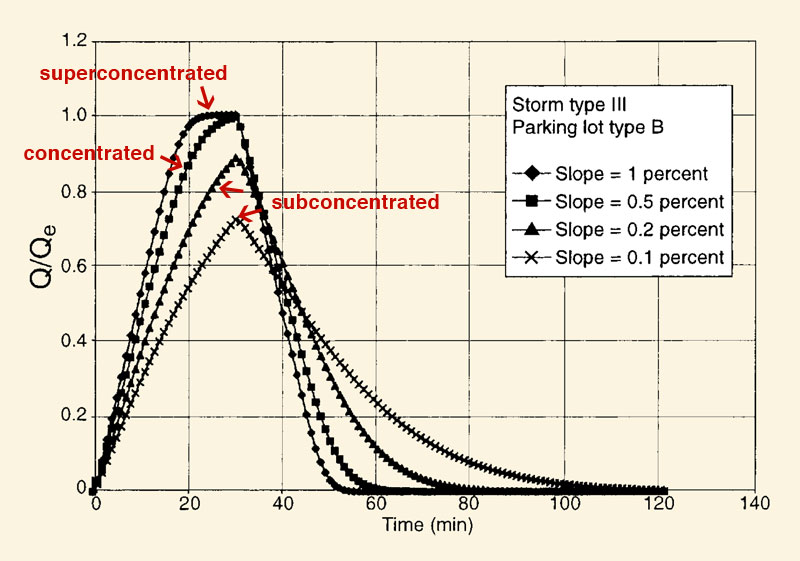
Overland flow calculation with the diffusion wave technique (Ponce and Klabunde).

Narrator: Victor M. Ponce

Music: Fernando Oñate

Editor: Flor Pérez

Copyright © 2010

Visualab Productions

All rights reserved