ENGINEERING HYDROLOGY: CHAPTER 044 - STORAGE CONCEPT OF OVERLAND FLOW

1. DISCHARGE-DEPTH RATING

1.01
The storage concept of overland flow is attributed to Horton.

1.02
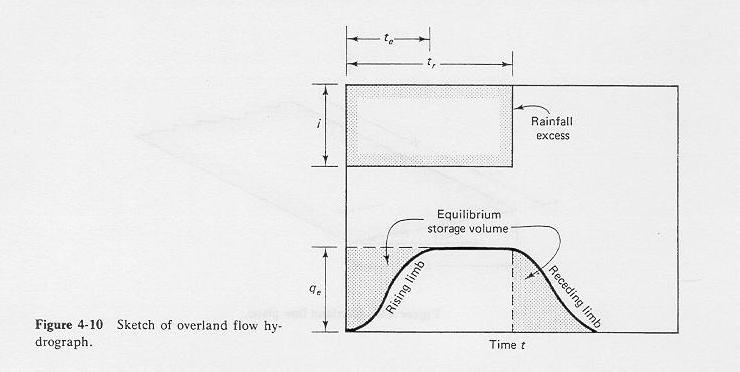
A sketch of the overland flow hydrograph is shown here.

1.03

1.04
The equilibrium storage volume is the area above the rising limb and below the equilibrium outflow q_e.

1.05
It is conceptually approximated as a triangular area as follows:

1.06

      q_e t_e
S_e =
        2

1.07
in which:
S_e= equilibrium storage volume
q_e= equilibrium outflow
t_e = time to equilibrium.

1.08
Horton noticed that experimental data justified a relation or rating between equilibrium outflow q_e and equilibrium storage S_e as follows:

1.09

q_e = a S_e^m

1.10
in which a and m are the coefficient and exponent of the rating, respectively.

1.11
The mean flow depth corresponding to the equilibrium storage is:

1.12

      S_e
h_e =
      L

1.13
in which L is the length of the overland flow plane.

1.14
The combination of these equations leads to the equilibrium discharge-depth rating:

1.15

q_e = b h_e^m

1.16
in which the constant b is:

1.17

b = a L^m

1.18
The rating exponent m characterizes the type of friction, either (1) turbulent, Chezy or Manning, (2) laminar, or (3) mixed laminar-turbulent flow.

1.19
Typical values of the rating exponent m are shown in the following table.

1.20

2. TIME TO EQUILIBRIUM

2.01
Combining the equilibrium storage-outflow rating with the equilibrium storage volume equation leads to a general expression for time to equilibrium of conceptual overland flow:

2.02

           2
t_e =
      q_e^(m-1)/m a^1/m

2.03
In the case of laminar flow, the coefficient b = a L^m = C_L, and the discharge-depth rating is:

2.04

q_e = C_L h_e^m

2.05
in which C_L is derived based on the mechanics of laminar flow on the overland flow plane:

2.06

      g S_O
C_L =
      3 ν

2.07
in which
g= gravitational acceleration,
S_o = plane slope, and
ν = kinematic viscosity of water.

2.08
By the runoff concentration principle, the equilibrium outflow from the overland flow plane is:

2.09

q_e = i L

2.10

in which i = rainfall excess.

2.11
Replacing q_e = iL, and a = C_L/L^m in the equation for time to equilibrium, and setting m = 3, leads to the time to equilibrium of laminar overland flow:

2.12

        2 L^1/3
t_e =
      i^2/3 C_L^1/3

2.13
For turbulent Manning friction, the coefficient of the rating is:

b = (1/n) S_o^1/2

2.14
Replacing q_e = iL, and b = a L^m = (1/n) S_o^1/2 in the equation for time to equilibrium, leads to the time to equilibrium of turbulent Manning overland flow:

2.15

        2 n^1/m L^1/m
t_e =
      i^(m-1)/m S_o^1/(2m)

2.16
Note that the time to equilibrium is directly proportional to friction and plane length, and inversely proportional to rainfall excess and plane slope.

2.17
For 100% turbulent Manning friction, m = 5/3, and the time of equilibrium is:

2.18

       2 n^0.6 L^0.6
t_e =
        i^0.4 S_o^0.3

2.19
This equation is of the same form as the Papadakis and Kazan formula for time of concentration, which was derived based on field data.

2.20

      0.66 n^0.52 L^0.50
t_c =
         i^0.38 S_o^0.31

2.21
The similarity in the exponents is remarkable.

2.22
Effectively, the concepts of time to equilibrium and time of concentration are one and the same.

2.23
The equation for time to equilibrium was derived by assuming the Manning formula, which is strictly applicable only for m = 5/3.

2.24
In practice, this equation is also used for mixed laminar-turbulent flow, with m varying in the range 5/3 to 3.

2.25
In addition, the shallow depths which prevail in overland flow result in a substantial increase in relative roughness.

2.26
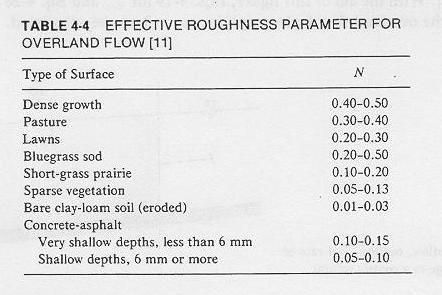
Consequently, an effective roughness parameter N much higher than Manning's n is used in overland flow computations.

2.27
Values of N are shown in the following table.

2.28

Narrator: Victor M. Ponce
Music: Fernando Oñate
Editor: Flor Pérez

Copyright © 2010
Visualab Productions
All rights reserved