1.04
The curve number method was developed based on 24-hr rainfall-runoff data.

1.05
It limits itself to the calculation of runoff depth, and does not explicitly take into account temporal variations of rainfall intensity.

1.06
The temporal rainfall distribution is introduced at a later stage, during the calculation of the flood hydrograph by means of unit hydrograph convolution.

2. RUNOFF CURVE NUMBER EQUATION

2.01
Potential runoff, that is, total rainfall, is referred to as P, and actual runoff as Q, with P ≥ Q.

2.02
The actual retention is P - Q.

2.03
The method defines a potential retention, or potential maximum retention S, with S ≥ P - Q.

2.04
The curve number method assumes a proportionality of retention and runoff, such that the ratio of actual retention P - Q to potential retention S is equal to the ratio of actual runoff Q to potential runoff P.

2.05

2.06
This equation was developed by Victor Mockus in the 1950s.

2.07
The runoff curve number equation is essentially a nonlinear fit to the rainfall-runoff data.

2.08
The use of the parameter potential maximum retention underscores the conceptual basis of the method.

2.09
The method defines an initial abstraction I_a as the amount of rainfall below where runoff is zero.

2.10
To account for initial abstraction, the curve number equation is modified to:

2.11

2.12
Solving for Q:

2.13

2.14
which is physically subject to the restriction
P ≥ I_a

2.15
This equation has two parameters: S and I_a

2.16
To simplify the equation and enhance its practical utility, NRCS expressed the initial asbtraction as a function of the potential retention as follows:

2.17

2.18
This equation was developed based on rainfall-runoff data from small experimental watersheds.

2.19
The coefficient 0.2 has been subjected to wide scrutiny.

2.20
Data has shown that this coefficient is likely to vary between 0.0 and 0.26.

2.21
However, 0.2 is the standard initial abstraction coefficient recommended by NRCS.

2.22
The standard runoff curve number equation is:

2.23

2.24
which is physically subject to the restriction
P ≥ 0.2 S

2.25

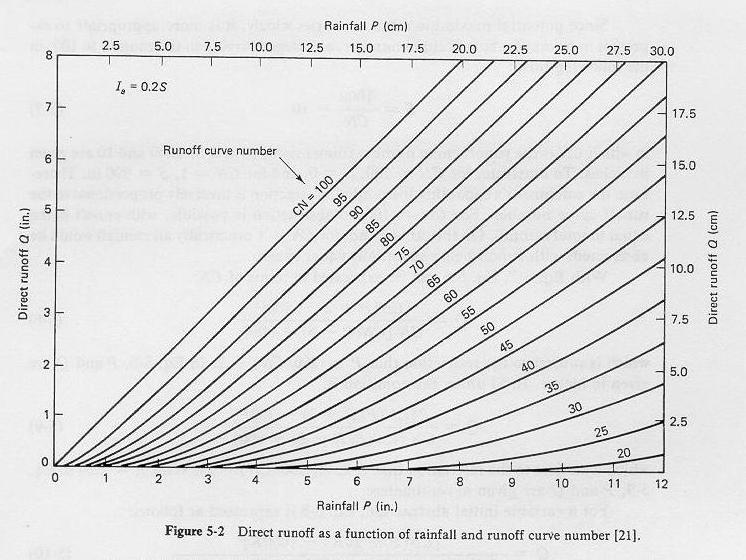
2.26
For research applications, particularly when warranted by field data, the standard 0.2 value can be relaxed. In this case:

2.27

2.28
with K = initial abstraction parameter.

3. RUNOFF CURVE NUMBER

3.01
Mockus expressed the potential retention S in terms of a surrogate parameter referred to as the curve number CN, varying in the range 1 to 100, as follows:

3.02

3.03
such that for CN = 1, it follows that S = 990 inches, an extremely large, and for practical purposes unreachable, value of potential retention.

3.04
Conversely, for CN = 100, it follows that S = 0, clearly the lower bound for potential retention.

3.05
In terms of CN, the standard runoff curve number equation is:

3.06

3.07
which is physically subject to the restriction
P ≥ (200/CN) - 2

3.08
In this equation, P and Q are given in inches.

3.09
In SI units, the equation is:

3.10

3.11
which is physically subject to the restriction
P ≥ R[(200/CN) - 2]

3.12
With R = 2.54 cm/inch, P and Q are given in centimeters.

3.13
With R = 25.4 mm/inch, P and Q are given in millimeters.

Narrator: Victor M. Ponce

Music: Fernando Oñate

Editor: Flor Pérez

Copyright © 2011

Visualab Productions

All rights reserved