1. STREAM CHANNEL ROUTING

1.01
Stream channel routing uses mathematical relations to calculate outflow from a stream channel once inflow, lateral contributions, and channel characteristics are known.

1.02
Stream channel routing refers to unsteady flow calculations in streams and channels.

1.03
Channel reach is a specific length of stream channel possessing certain translation and storage properties.

1.04
The hydrograph at the upstream end of the reach is the inflow hydrograph.

1.05
The hydrograph at the downstream end is the outflow hydrograph.

1.06
Lateral contributions consist of point tributary flow and/or distributed inflows from overland flow or from exfiltration from groundwater flow.

1.07
The terms stream channel routing and flood routing are often used interchangeably.

1.08
This is because most stream channel routing applications are in flood flow analysis, flood control design, or flood forecasting.

1.09
There are two types of stream channel routing: (1) hydrologic, and (2) hydraulic.

1.10
Hydrologic stream channel routing is based on the storage concept.

1.11
Hydraulic channel routing is based on the principles of mass and momentum conservation.

1.12
Hydraulic routing techniques are of three types: (1) kinematic wave, (2) diffusion wave, and (3) dynamic wave.

1.13
The dynamic wave is the most complete model of unsteady open-channel flow.

1.14
Kinematic and diffusion waves are convenient and practical approximations to the dynamic wave.

2. HYDROLOGIC MODELING

2.01
A typical hydrologic model consists of: (1) system, (2) input, and (3) output.

2.02
In surface water hydrology, the system is usually a catchment, a reservoir, or a stream channel.

2.03
In the case of a catchment, the input is a storm hyetograph.

2.04
For reservoirs and channels, the input is an inflow hydrograph.

2.05
For all three cases, catchments, reservoirs, and channels, the output is an outflow hydrograph.

2.06
Modeling problems are classified into three types: (1) prediction, (2) calibration, and (3) inversion.

2.07
In the prediction problem, input and system are known and described by properties or parameters, and the task is to calculate the output.

2.08
For instance, with known inflow hydrograph, lateral contributions, and channel reach parameters, the outflow hydrograph can be computed using routing techniques.

2.09
In the calibration problem, inflow and outflow are known, and the objective is to determine the properties or parameters describing the system.

2.10
In the case of a stream channel, with known upstream inflow, lateral contributions, and outflow hydrograph, the routing parameters are calculated by a calibration procedure.

2.11
The inversion problem is the third type of modeling problem.

2.12
In this case, system and output are known, and the task is to calculate the inflow or inflows.

2.13
This is accomplished by a technique known as inverse channel routing.

2.14
For instance, with known upstream inflow, outflow, and channel reach parameters, the lateral contributions can be calculated by inverse routing.

2.15
The prediction problem is the most common type of modeling application.

2.16
A calibration may be required in advance of the prediction.

2.17
Model verification tests the model with actual data to establish its predictive accuracy.

2.18
To calibrate and verify a model, two sets of data are needed.

2.19
The first set is used in model calibration; the second set in model verification.

2.20
A close agreement between calculated and measured data is an indication that the model has been verified.

3. MUSKINGUM METHOD

3.01
The Muskingum method of flood routing was developed in the 1930s in connection with the design of flood control schemes in the Muskingum River Basin, Ohio.

3.02
It is the most widely used method of hydrologic stream channel routing, with numerous applications in the United States and throughout the world.

3.03
The method is based on the differential equation of storage:

3.04

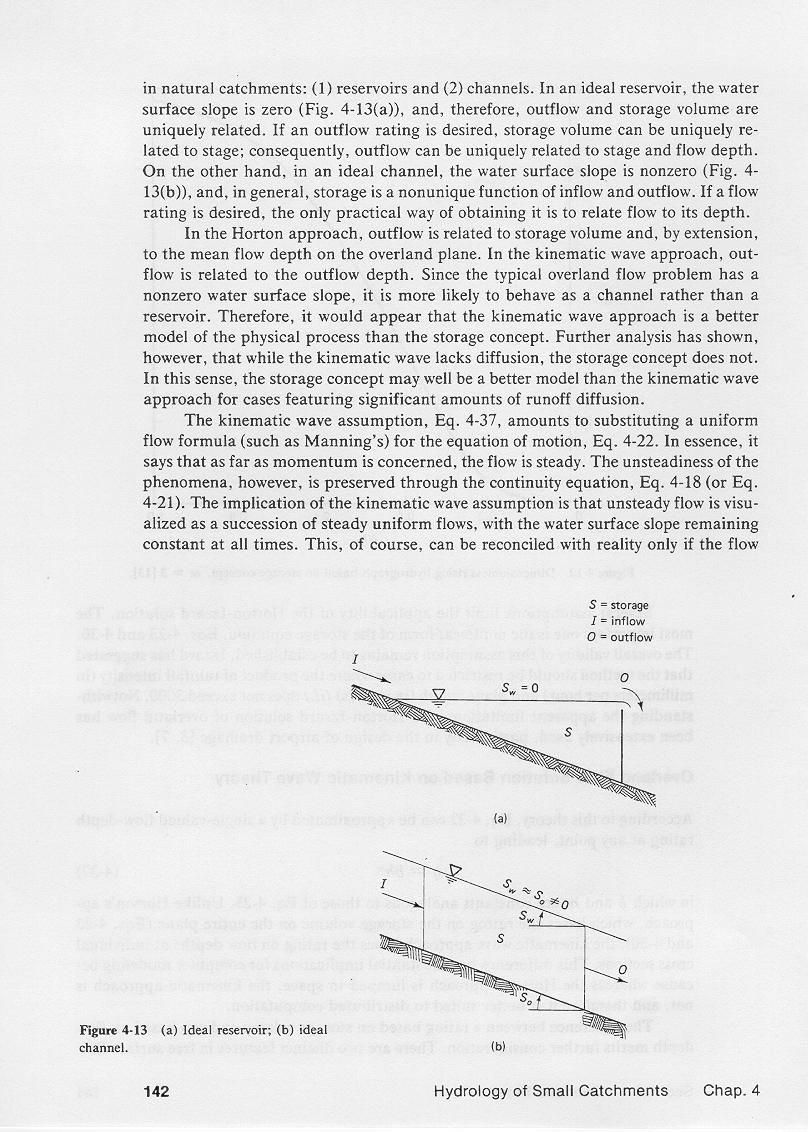
3.05
In an ideal channel, storage is a function of inflow and outflow.

3.06
This is in contrast with ideal reservoirs, in which storage is solely a function of outflow.

3.07
In the Muskingum method, storage is a linear function of inflow and outflow:

3.08

3.09
in which S = storage volume, I = inflow, O = outflow, K = a time constant or storage coefficient, and X = a dimensionless weighting factor.

3.10
With inflow and outflow in cubic meters per second, and K in hours, storage volume is in (m³/s)-hr.

3.11
Alternatively, for K in seconds, storage volume is in cubic meters.

3.12
The Muskingum equation was developed by McCarthy in 1938.

3.13
It is a generalization of the linear reservoir concept.

3.14
For X = 0, the Muskingum equation reduces to a linear storage-outflow relation.

3.15
In other words, a linear reservoir is a special case of the Muskingum method, for X = 0.

3.16
To derive the Muskingum routing equation, the differential equation of storage is discretized on the x-t plane to yield:

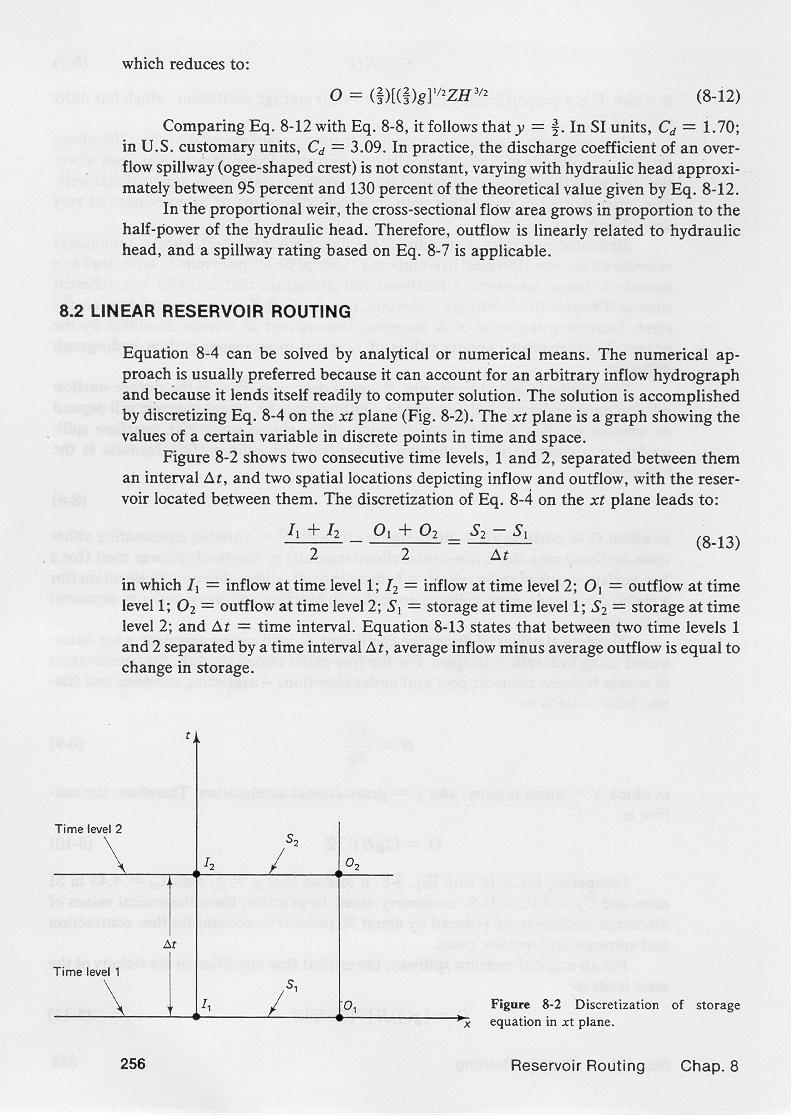
3.17

3.18
where Δt = time interval.

3.19
The storage equation is expressed at time levels 1 and 2:

3.20

3.21

3.22
Substituting these equations into the discretized equation of storage, the Muskingum routing equation is obtained:

3.23

3.24
in which C₀, C₁, and C₂ are routing coefficients defined in terms of Δt, K, and X as follows:

3.25

3.26

3.27

3.28
Since the sum of the three routing coefficients is equal to 1:

3.29

3.30
the routing coefficients are interpreted as weighting coefficients.

3.31

4. METHODOLOGY

4.01
The Muskingum method will calculate an outflow hydrograph, given an inflow hydrograph, an initial condition, and the routing parameters K and X.

4.02
At the start, a time interval Δt is chosen.

4.03
Using the chosen time interval, the temporal domain is divided into time steps, and the inflow hydrograph is discretized into corresponding values at every time step.

4.04
The chosen time interval should be small enough so that the actual inflow hydrograph is properly represented by the discrete values.

4.05
For this purpose, the time interval should be at least 1/10 of the time to peak of the inflow hydrograph.

4.06
The methodology consists of the following steps:

4.07
1. Calculate the routing coefficients based on Δt, K and X.

4.08
2. Calculate the outflow hydrograph using the Muskingum routing equation recursively, from n = 1, to n = number of time steps.

4.09

4.10
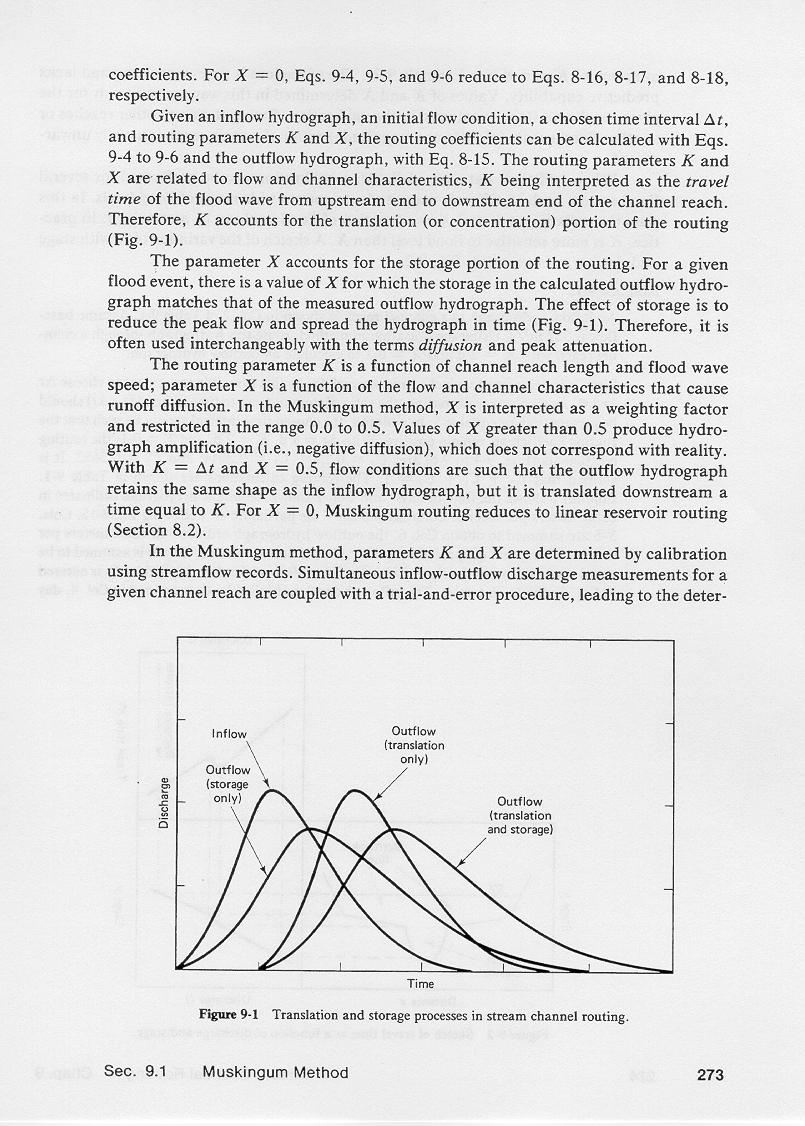
The routing parameters K and X are related to flow and channel characteristics.

4.11
K is interpreted as the travel time of the flood wave from upstream end to downstream end of the channel reach.

4.12
Therefore, the parameter K accounts for the translation portion of the routing, as shown here.

4.13
Conversely, the parameter X accounts for the storage portion of the routing.

4.14
For a given flood event, there is a value of X for which the storage in the calculated outflow hydrograph matches that of the measured outflow hydrograph.

4.15
The effect or storage is to reduce the peak flow and to spread the hydrograph in time.

4.16
Therefore, it is often used interchangeably with the terms diffusion and peak attenuation.

4.17
The parameter K is a function of channel reach length and flood wave speed.

4.18
The parameter X is a function of the flow and channel characteristics that produce runoff diffusion.

4.19
In the Muskingum method, X in interpreted as a weighting factor, and restricted in the range 0.0 to 0.5.

4.20
Values of X greater than 0.5 produce hydrograph amplification, that is, negative diffusion, which does not correspond with reality.

4.21
With Δt = K, and X = 0.5, flow conditions are such that the outflow hydrograph retains the same shape as the inflow hydrograph, but it is translated downstream a time equal to K.

4.22
For X = 0, the Muskingum method reduces to linear reservoir routing.

4.23
In the Muskingum method, the routing parameters K and X are determined by calibration using streamflow records.

4.24
Simultaneous inflow-outflow discharge measurements for a given channel reach are coupled with a trial-and-error procedure, leading to the determination of K and X.

4.25
However, strictly speaking, the values of K and X determined in this way are valid only for the given reach and flood event used in the calibration.

4.26
Extrapolation to other reaches or to other flood events within the same reach, while practical, is generally unwarranted.

4.27
When sufficient data is available, a calibration can be performed, within the same reach, for several flood events of different magnitude, to cover a wide range of flood stages.

4.28
In this way, the variation of K and X as a function of flood level can be approximately ascertained.

4.29
In practice, K is more sensitive to flood level than X.

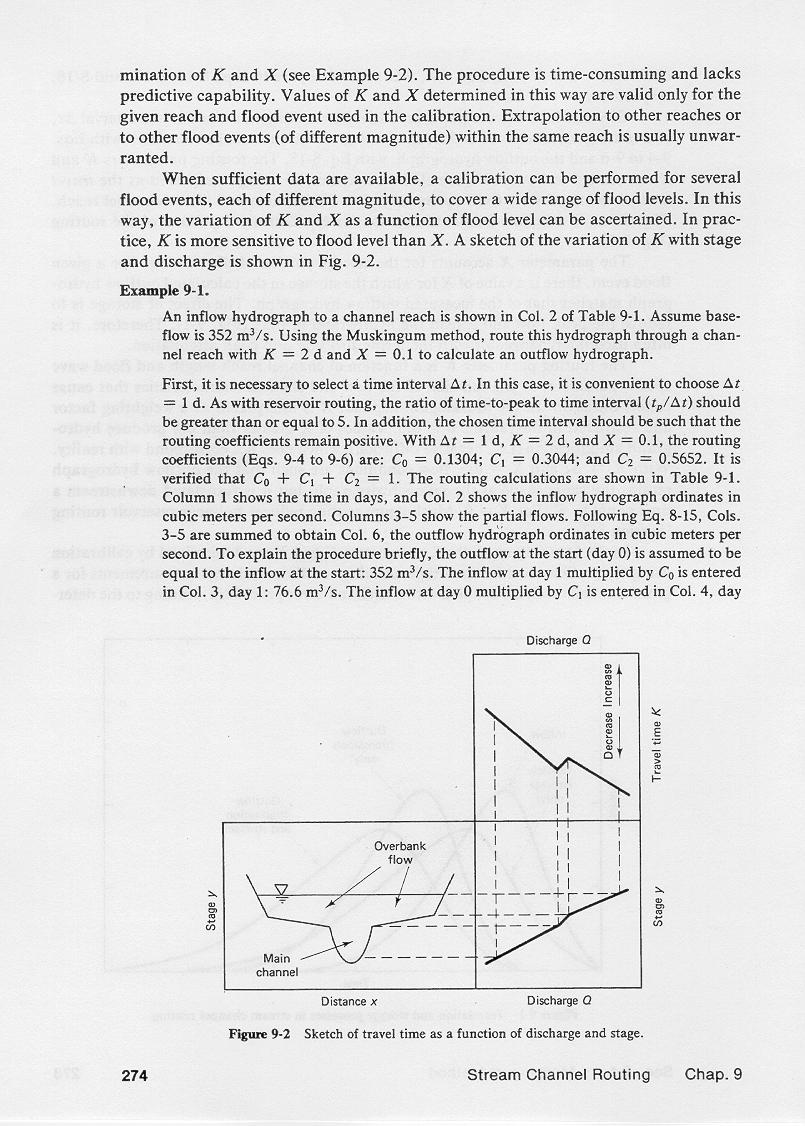
4.30
A sketch of the variation of travel time K with stage and discharge is shown here.

4.31
In a typical channel cross section featuring a wide range of flow levels, the travel time tends to decrease with an increase in inbank flow, increase with an increase in overbank flood stages, and again decrease with an increase in very high flood stages.

5. EXAMPLE

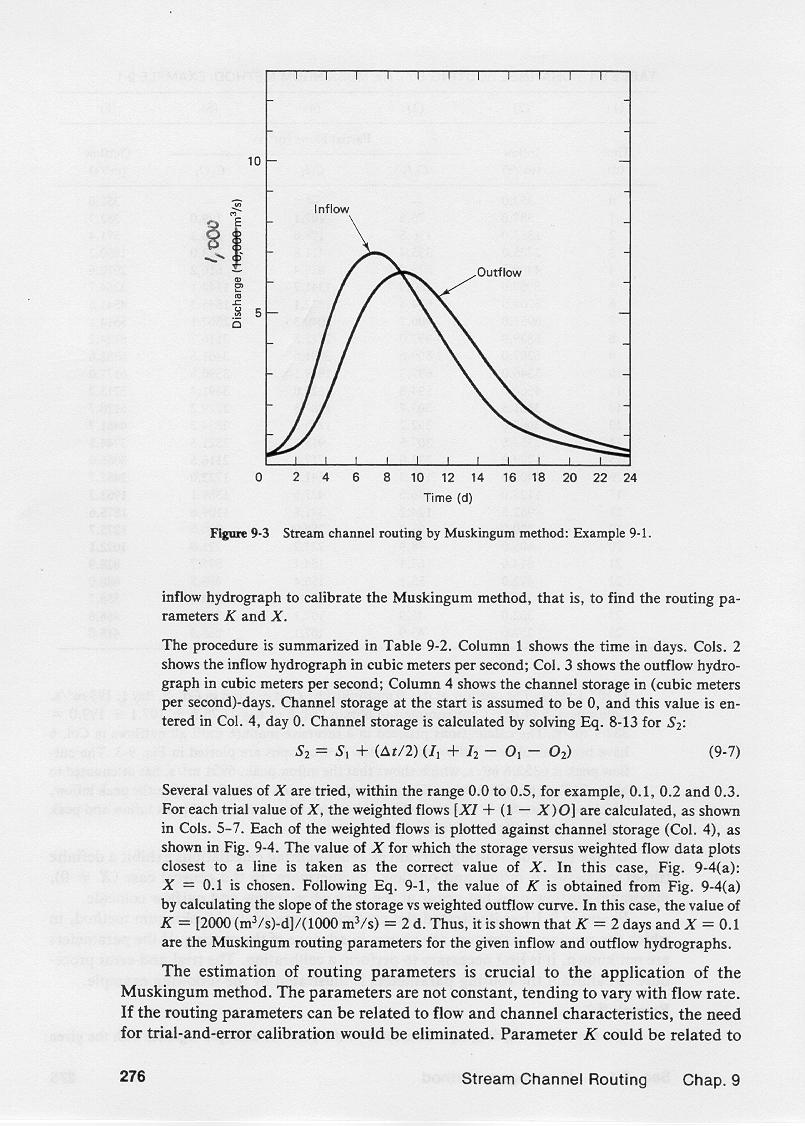
5.01
The application of the Muskingum method to route a flood wave is shown in the following example.

5.02
Assume the inflow hydrograph shown in this table, with baseflow equal to 352 m³/s, travel time K = 2 days, weighting factor X = 0.1, and time interval Δt = 1 day.

5.03
The routing parameters are calculated as C_O = 0.13, C₁ = 0.30, and C₂ = 0.57, confirming that they add up to 1.

5.04
Column 1 shows the time in days.

5.05
Column 2 shows the inflow hydrograph in m³/s.

5.06
Columns 3 to 5 show the partial flows.

5.07
Column 6 shows the outflow hydrograph, calculated as the sum of Columns 3, 4 and 5.

5.08
The peak inflow is 6951 m³/s at time equal to 7 days.

5.09
The peak outflow is 6352.6 m³/s, at time equal to 9 days.

5.10
Note that the peak outflow is about 91% of the peak inflow.

5.11
The time elapsed between peak inflow and peak outflow is 2 days, equal to the travel time K.

5.12
The inflow and outflow hydrographs are shown here.

5.13
Unlike reservoir routing, stream channel calculations exhibit a definite lag between the start of inflow and the start of outflow.

5.14
This is due to the finite travel time of flood discharges in stream channels.

5.15
Furthermore, in the general case, where X is not equal to zero, maximum outflow does not occur at the time where inflow and outflow coincide.

5.16
The preceding example has illustrated the predictive stage of the Muskingum method, where the routing parameters are known in advance of the actual routing.

5.17
When the parameters are unknown, it is first necessary to perform a calibration.

6. CALIBRATION

6.01
To perform a calibration, the Muskingum method requires both inflow and outflow hydrographs.

6.02
Essentially, the calibration identifies the routing parameters, that is, it is a system identification.

6.03
To perform the calibration, the discretized differential equation of storage:

6.04

6.05
is expressed as follows:

6.06

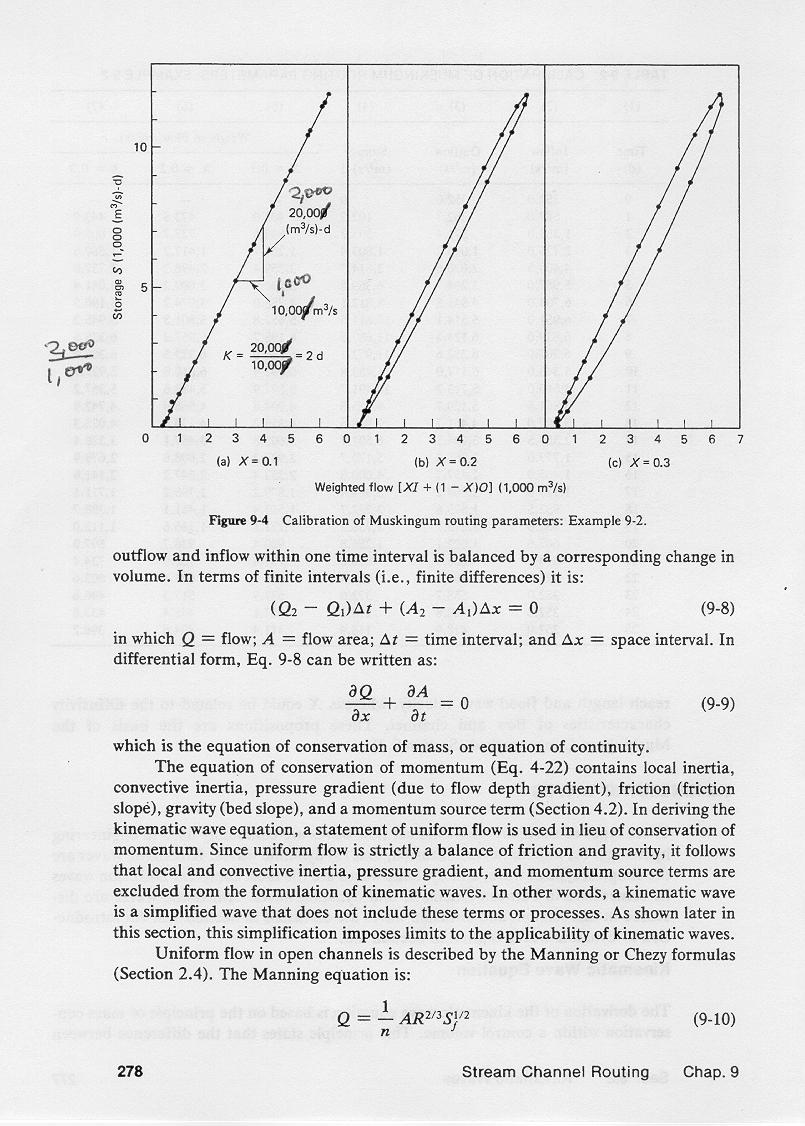
6.07
Several values of X are tried, within the allowable range of 0.0-0.5; for example, 0.1, 0.2, and 0.3.

6.08
For each trial value of X, the weighted flows are calculated, and plotted against storage.

6.09

6.10
The computations are shown in this table.

6.11
Column 1 shows the time in days.

6.12
Column 2 shows the inflow hydrograph.

6.13
Column 3 shows the outflow hydrograph.

6.14
Column 4 shows the storage calculated with this formula:

6.15

6.16
Columns 5 to 7 show the weighted flows for X = 0.1, 0.2, and 0.3, respectively, calculated at level n+1:

6.17

6.18
Each of the weighted flows is plotted against storage, as shown here.

6.19
The correct value of X is that for which the storage vs weighted flow data plots closest to a straight line.

6.20
In this case, X = 0.1 is the correct value.

6.21
The value of K is the slope of the storage vs weighted flow line.

6.22
In this case, K = 2 days.

6.23
Thus, we confirm, by back calculation, that the Muskingum routing parameters for this problem are K = 2 days, and X = 0.1.

6.24

6.25

6.26

6.27

6.28

6.29

6.30

Narrator: Victor M. Ponce

Music: Fernando Oñate

Editor: Flor Pérez

Copyright © 2011

Visualab Productions

All rights reserved