1. KINEMATIC WAVE EQUATION

1.01
Three types of unsteady open-channel flow waves are commonly used in engineering hydrology: (1) kinematic, (2) diffusion, and (3) dynamic.

1.02
Kinematic waves are the simplest type of wave, and dynamic waves are the most complex.

1.03
Diffusion waves lie somewhere in between kinematic and dynamic waves.

1.04
The kinematic wave equation is based on the principle of mass conservation within a control volume.

1.05
This principle states that the difference between outflow and inflow within one time interval is balanced by a corresponding change in volume.

1.06
In terms of finite differences:

1.07

1.08
in which Q = flow, A = flow area, Δt = time interval, and Δx = space interval.

1.09
In differential form, this equation can be written as follows:

1.10

1.11
This is the equation of conservation of mass, or equation of continuity.

1.12
The equation of conservation of momentum contains (1) local inertia, (2) convective inertia, (3) pressure, or flow depth gradient, (4) friction, (5) gravity, and (6) momentum source term.

1.13
In the kinematic wave equation, a statement of uniform flow is used in lieu of the conservation of momentum.

1.14
Uniform flow is strictly a balance of gravity and friction.

1.15
Therefore, the rest of the terms, including pressure gradient, inertia, and momentum source are excluded from the formulation.

1.16
In other words, a kinematic wave is a simplified wave that does not include these terms of processes.

1.17
This simplification imposes certain limits on the applicability of the kinematic wave.

1.18
Uniform flow in open channels is described by the Manning or Chezy formulas.

1.19
The Manning equation is:

1.20

1.21
in which R = hydraulic radius, in meters, S_f = friction slope, in meters per meter, and n = Manning friction coefficient.

1.22
The hydraulic radius is:

1.23

1.24
in which P = wetted perimeter.

1.25
Substituting the hydraulic radius into the Manning equation leads to:

1.26

1.27
Assume for simplicity that n, S_f and P are constant.

1.28
This is the case of a hydraulically wide channel, where the wetted perimeter may be assumed to be independent of flow area.

1.29
Assuming a rating equation of the following type:

1.30

1.31
It follows that α is:

1.32

1.33
and β is:

1.34

1.35
Differentiating the rating equation with respect to flow area leads to the wave celerity:

1.36

1.37
in which V = mean flow velocity.

1.38
Multiplying the continuity equation with the wave celerity, and applying the chain rule of differentiation, leads to the kinematic wave equation:

1.39

1.40
Or, alternatively:

1.41

1.42
These equations describe the movement of waves that are kinematic in nature.

1.43
These are referred to as kinematic waves, that is, waves for which inertia and the flow depth gradient have been neglected.

1.44
The kinematic wave equation is a first-order partial differential equation.

1.45
Therefore, kinematic waves travel with celerity dQ/dA and do not attenuate.

1.46
Wave attenuation, that is wave diffusion, can be described only by a second-order partial differential equation.

1.47
The absence of attenuation in a kinematic wave can be further explained by the following mathematical argument.

1.48
Since dQ/dA is the celerity of the unsteady wavelike features of the flow, it can be replaced by dx/dt:

1.49

1.50
Therefore:

1.51

1.52
which is a statement of the total derivative dQ/dt.

1.53

1.54
Since the right-hand side of this equation is zero, it follows that dQ/dt = 0, that is, discharge Q remains constant in time for waves traveling with celerity dQ/dA.

1.55
This is interpreted as the lack of diffusion of a kinematic wave.

1.56
The kinematic wave equation is a nonlinear first-order partial differential equation describing the change of discharge in time and space.

1.57
Its is nonlinear because the wave celerity varies with discharge.

1.58
However, the nonlinearity is usually small, and therefore, the kinematic wave equation can be solved in a linear mode by considering the wave celerity to be constant.

1.59
The solution of the kinematic wave can be accomplished by analytical or numerical means.

1.60
The simplest kinematic wave solution is a linear numerical solution.

2. NUMERICAL SCHEMES

2.01
Numerical schemes are discrete formulations, on the x-t plane, of the governing differential equations.

2.02
The order of accuracy of a numerical scheme measures the ability of the scheme to reproduce the terms of the differential equation.

2.03
In general, the higher the order of accuracy of the scheme, the better it is able to reproduce the terms of the differential equation.

2.04
Forward and backward finite differences have first-order accuracy, that is, discretization errors of first order.

2.05
Central differences have second order accuracy, with discretization errors of second order.

2.06
The numerical solution of the kinematic wave equation with first-order schemes creates numerical diffusion and dispersion, while second order schemes create only numerical dispersion.

2.07
Numerical diffusion is caused by first-order discretization errors; numerical dispersion by second-order errors.

2.08
A third-order scheme of the kinematic wave equation provides the exact solution, creating neither numerical diffusion nor dispersion.

2.09
Numerical diffusion and/or dispersion are caused by the finite size of the grid and not necessarily related to the physical problem.

3. SECOND-ORDER SCHEME

3.01
The discretization of the kinematic wave equation with a linear, second-order accurate scheme, using central differences in time and space, leads to the following routing equation:

3.02

3.03
in which the routing coefficients are:

3.04

3.05

3.06
and C is the Courant number, defined as follows:

3.07

3.08
Note that the Courant number is the ratio of physical wave celerity βV to grid celerity Δx/Δt.

3.09
The Courant number is a fundamental concept in the numerical solution of hyperbolic partial differential equations such as the kinematic wave equation.

3.10
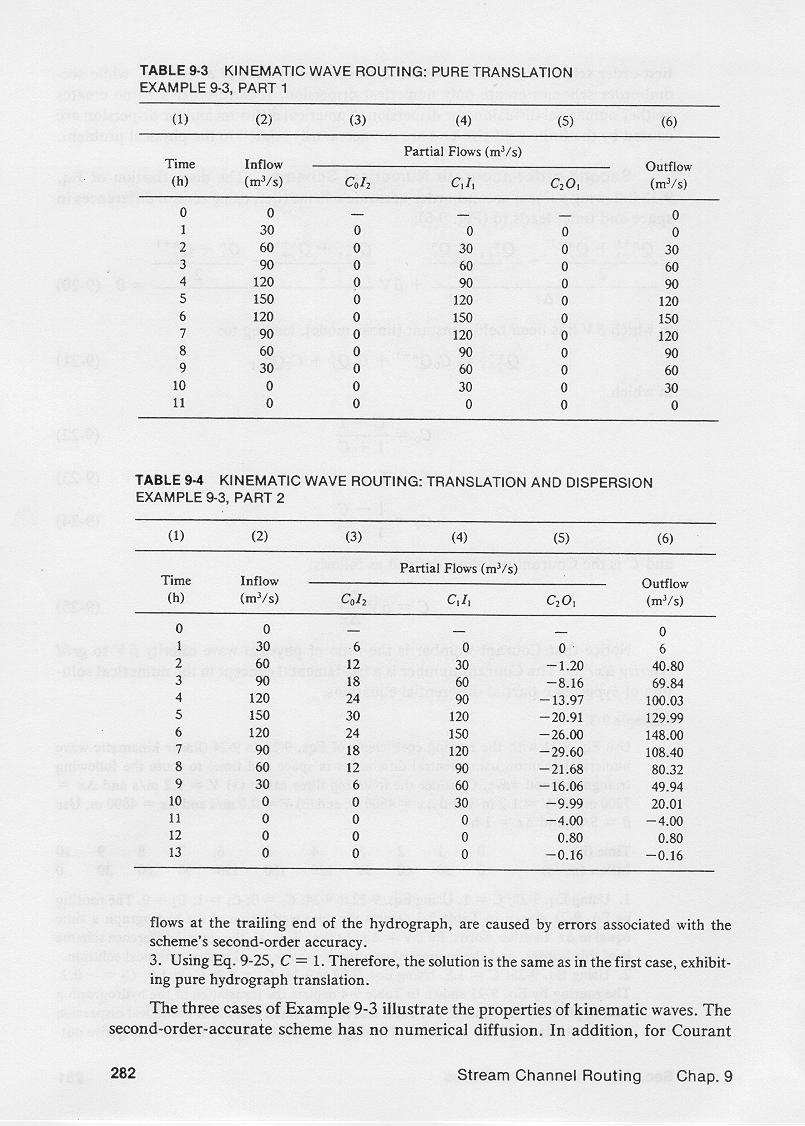
This table shows the kinematic wave routing of an inflow hydrograph, with wave celerity and space and time intervals such that the Courant number C = 1.

3.11
The table shows the exact translation of the hydrograph, reproducing the exact solution of the kinematic wave.

3.12
This other table shows the kinematic wave routing of an inflow hydrograph, with wave celerity and space and time intervals such that the Courant number C = 1.5.

3.13
In this case, the outflow hydrograph is diffused to a peak of 148 m³/s, as compared to an inflow of 150 m³/s.

3.13
Also, the outflow hydrograph is dispersed, with unrealistic negative outflows present at the tail of the hydrograph.

3.14
We conclude that the second-order accurate numerical solution of the kinematic linear wave equation is impractical, because it only works well for the trivial case of Courant number C = 1.

4. FIRST-ORDER SCHEME

4.01
The discretization of the kinematic wave equation with a linear, first-order accurate scheme, using backward differences in both time and space, leads to the following routing equation:

4.02

4.03
in which the routing coefficients are:

4.04

4.05

4.06
This table shows the kinematic wave routing of an inflow hydrograph, with wave celerity and space and time intervals such that the Courant number C = 1.

4.07
The table shows that in this case, the outflow hydrograph for C = 1 is translated and diffused, with the peak outflow at 120.93 m³/s, as compared to a peak inflow of 150 m³/s.

4.08
Additionally, the time base has increased from 10 hr to more than 15 hr.

4.09
The conclusion is that different schemes for solving the kinematic wave equation lead to different answers, depending on the amount of numerical diffusion and dispersion.

4.10

4.11

4.12

4.13

4.14

Narrator: Victor M. Ponce

Music: Fernando Oñate

Editor: Flor Pérez

Copyright © 2011

Visualab Productions

All rights reserved