1. RATIONALE

1.01
The Clark unit hydrograph dates back to 1945.

1.02
Clark noticed that a hydrograph developed for a unit effective rainfall using the time-area method lacked storage, that is, diffusion.

1.03
Tuus, he proposed routing the time-area unit hydrograph through a linear reservoir, to provide a certain amount of diffusion to better simulate the response of a natural catchment.

1.04
Effectively, Clark's unit hydrograph methodology involves two steps: (1) translation, accomplished with the time-area method, and (2) diffusion, by using a linear reservoir.

1.05
The translated-only unit hydrograph is obtained with the time-area methodology.

1.06
The translated-and-diffused unit hydrograph is obtained by routing the time-area unit hydrograph through a linear reservoir.

2. METHODOLOGY

2.01
The Clark procedure is a combination of unit hydrograph, time-area, and linear reservoir concepts.

2.02
First, the catchment isochrones are determined.

2.03
A unit effective rainfall is used as input, which produces a unit hydrograph as outflow.

2.04
This outflow is routed through a linear reservoir.

2.05
An estimate of the storage constant K is required.

2.06
This can be obtained either from the tail of a measured hydrograph, or by using a regionally derived formula.

2.07
In the latter case, the Clark unit hydrograph can be properly regarded as a synthetic unit hydrograph.

2.08
The Clark method has the advantage that the catchment properties, that is, shape, hydraulic length, and surface roughness, are reflected in the time-area histogram and, therefore, on the shape of the unit hydrograph.

2.09
In practice, this feature has contributed to the popularity of the Clark unit hydrograph.

2.10
When using the Clark unit hydrograph or time-area methods, the storage constant K can be estimated by calibration, from the tail of a measured hydrograph.

2.11
For this purpose, the differential equation of storage is recalled:

2.12

2.13
This equation is evaluated at the time for which inflow equals zero, that is, past the end of the translated-only hydrograph.

2.14
Alternatively, it can be evaluated at the point of inflection on the receding limb of a measured hydrograph.

2.15
For inflow equal to zero, the differential equation of storage reduces to:

2.16

2.17
Since, by definition, outflow and storage are linearly related:

2.18

2.19
The following expression for K is obtained:

2.20

2.21
Thus, K can be evaluated as the negative ratio of outflow and rate of change of outflow at or after the end of the translated-only hydrograph.

2.22
Alternatively, these values can be evaluated at the point of inflection on the receding limb of a measured hydrograph.

3. EXAMPLE

3.01
The Clark unit hydrograph methodology is illustrated by the following example.

3.02
A 2-hr Clark unit hydrograph for a 100-km² catchment is desired, with time of concentration 4 hr, and isochrones and time-area histogram as shown here.

3.03
Assume K = 2 hr.

3.04
The applicable time interval Δt is that of the time-area histogram, that is, 1 hr.

3.05
For a 2-hr unit hydrograph, the unit rainfall is 0.5 cm/hr, lasting 2 hr.

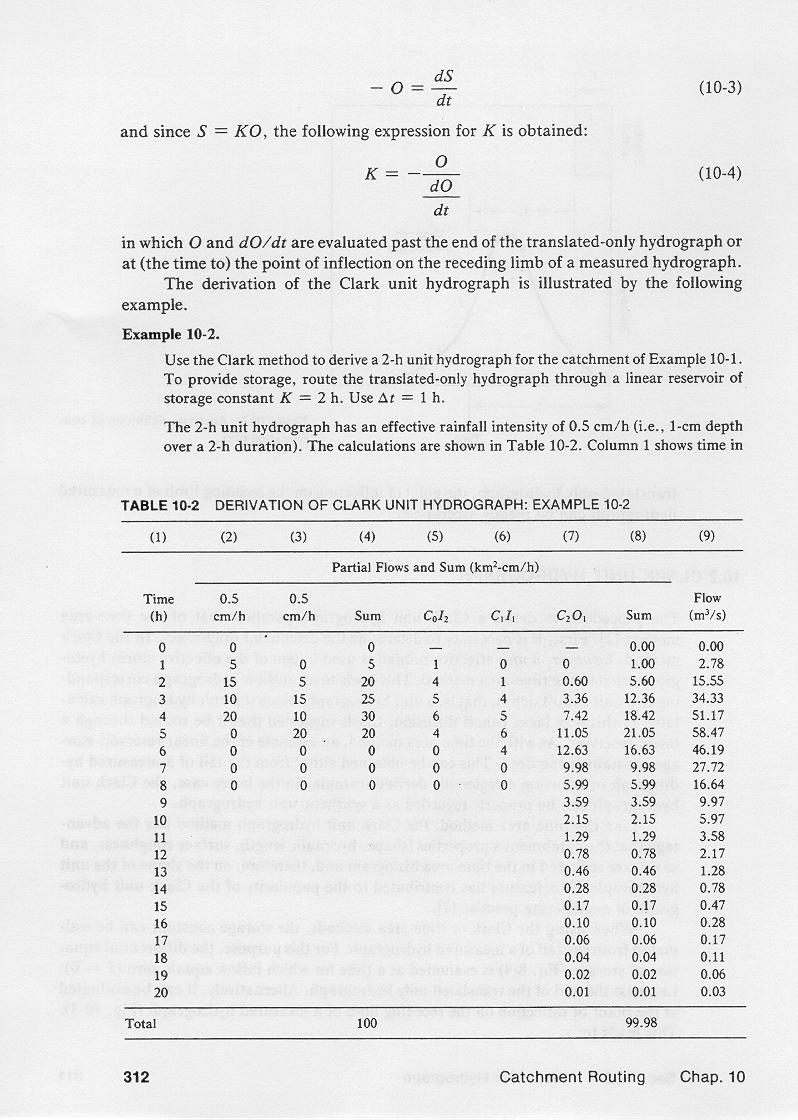
3.06
The calculations are shown in this table.

3.07
Column 1 shows the time in hours.

3.08
Columns 2 and 3 show the partial flows obtained by applying the time-area method, with unit rainfall 0.5 cm/hr and given time-area histogram, in km²-cm/hr discharge units.

3.09
Note that since the histogram time interval is 1 hr, and the unit hydrograph duration is 2 hr, two 1-hr increments of unit rainfall are required, shown in Columns 2 and 3.

3.10
Column 4 shows the sum of the time-area partial flows.

3.11
Columns 5, 6, and 7 show the partial flows of the linear reservoir routing.

3.12
Column 8 shows the sum of the partial flows of Columns 5 to 7, in km²-cm/hr discharge units.

3.13
Column 9 is Column 8 multiplied by 2.78, to convert to m³/s.

3.14
Column 9 is the Clark unit hydrograph for the given catchment.

3.15
Note that the peak of the translated-only unit hydrograph, in Column 4, time = 4 hr, is 30 km²-cm/hr, while the peak of the translated-and-diffused unit hydrograph, in Column 8, time = 5 hr, is 21.05 km²-cm/hr.

3.16
Thus, the diffusion in the hydrograph ordinates provided by the linear reservoir amounts to about 30%.

3.17
Also, note that the translated-only unit hydrograph ends sharply at 6 hr, with a time base of 6 hr, while the translated-and-diffused unit hydrograph is much diffused, with the time base extending to about 20 hr.

3.18
This confirms the substantial amount of runoff diffusion provided by the linear reservoir.

4. CALIBRATION OF K

4.01
The linear reservoir storage constant can be calculated directly from the tail of a measured hydrograph.

4.02
To illustrate the procedure, in this table, the translated-only hydrograph of Column 4 has zero ordinates at the tail, that is, for t = 6 hr and t = 7 hr.

4.03
Therefore, the equation for K can be applied between t = 6 hr and t = 7 hr.

4.04
The average outflow for these time steps, taken from Column 9, is:

4.05

4.06
The rate of change of outflow is:

4.07

4.08
Therefore, the storage constant is:

4.09

4.10
It is confirmed that the storage constant for this outflow hydrograph is K = 2 hr.

4.10
The equation for K applies only at the tail of the outflow hydrograph, after the translated-only hydrograph has receded back to zero.

4.11
The Clark parameter K can be estimated based on catchment characteristics.

4.12
This effectively qualifies the Clark unit hydrograph as a synthetic unit hydrograph.

4.13

Narrator: Victor M. Ponce

Music: Fernando Oñate

Editor: Flor Pérez

Copyright © 2011

Visualab Productions

All rights reserved