OPEN-CHANNEL HYDRAULICS: LECTURE 013 - FLOW REGIMES

1. VELOCITY NUMBERS
1.01
Velocity refers to the mean velocity of steady uniform, equilibrium or gradually varied flow.
1.02
Celerity refers to the speed of wavelike features of the unsteady motion.
1.03
There are three speeds in open channel flow:
1. The velocity of steady flow, calculated with the Manning formula.
2. The celerity of kinematic waves, calculated with the Seddon formula.
3. The celerity of dynamic waves, calculated with the Lagrange formula.
1.04
The Manning equation is:
1.05

     1
v =
R^2/3 S_f^1/2
     n

1.06
in which v = mean velocity, R = hydraulic radius, S = friction slope, and n = friction coefficient.
1.07
The dynamic wave celerity, or Lagrange celerity, is:
1.08

c_d = v +-(gh)^1/2

1.09
in which c_d = dynamic wave celerity, h = flow depth, and g = gravitational acceleration.
1.10
The relative dynamic wave celerity is:
1.11

c_d,r = (gh)^1/2

1.12
The kinematic wave celerity, or Seddon celerity, is:
1.13

c_k = β v

1.14
in which β is the exponent of the discharge-area rating:
1.15

Q = α A^β

1.16
The relative kinematic wave celerity is:
1.17

c_k,r = (β - 1) v

1.18
These three velocities give rise to two independent velocity ratios.
1.19
These ratios are referred to as the Froude number and the Vedernikov number.
1.20
The Froude number is the ratio of mean flow velocity to relative dynamic wave celerity.
1.21

       v
F =

     (gh)^1/2

1.22
Values of Froude number less than 1 describe subcritical flow.
1.23
Values of Froude greater than 1 describe supercritical flow.
1.24
A value of Froude number equal 1 describes critical flow.
1.25
The flow is subcritical when dynamic waves travel faster than the mean velocity.
1.26
In this case, wave disturbances can propagate upstream; therefore, the flow is controlled from the downstream boundary.
1.27
The flow is supercritical when dynamic waves travel slower than the mean flow velocity.
1.28
In this case, wave disturbances cannot propagate upstream; therefore, the flow is controlled from the upstream boundary.
1.29
The flow is critical when the mean flow velocity and dynamic waves travel at the same speed.
1.30
In this case, wave disturbances remain stationary.
1.31
The Vedernikov number is the ratio of relative kinematic wave celerity to relative dynamic wave celerity.
1.32

     (β - 1) v
V =

       (gh)^1/2

1.33
Values of Vedernikov number less than 1 describe stable flow, in which disturbances are attenuated.
1.34
Values of Vedernikov number greater than 1 describe unstable flow, in which disturbances are amplified.
1.35
Values of Vedernikov number equal to 1 describe neutrally stable flow, in which disturbances are neither attenuated nor amplified.
1.36
In practice, values of the Vedernikov number greater than 1 produce a phenomenon referred to as roll waves, characterized by a train of small waves travelling downstream.
1.37
Roll waves occur in steep, hydraulically wide channels.
1.38
Roll waves on the spillway at Turner dam, San Diego County, California, on February 24, 2005.
1.39
The ratio of Vedernikov and Froude numbers is:
1.40

V

= β - 1
F

1.41
β is the exponent of the discharge-area rating, varying with type of friction and cross-sectional shape.
1.42
β characterizes the neutrally stable Froude number, that is, the Froude number for which the Vedernikov number is equal to 1.
1.43

         1
F_ns =

       β - 1

1.44
This table shows the neutrally stable Froude number for various types of friction and cross-sectional shape.
1.45

Type of friction and/or cross-sectional shape β F_ns

Laminar 3 1/2

Turbulent Manning, hydraulically wide 5/3 3/2

Turbulent Chezy, hydraulically wide 3/2 2

Turbulent Manning, triangular 4/3 3

Turbulent Chezy, triangular 5/4 4

Inherently stable 1 ∞

1.46
The special case of β = 1, for which the neutrally stable Froude number is infinity, is referred to as the inherently stable channel.
1.47
In the inherently stable channel, the hydraulic radius is a constant.
1.48
Roll waves do not develop in an inherently stable channel.
1.49
The shape of the inherently stable channel is shown here.
1.50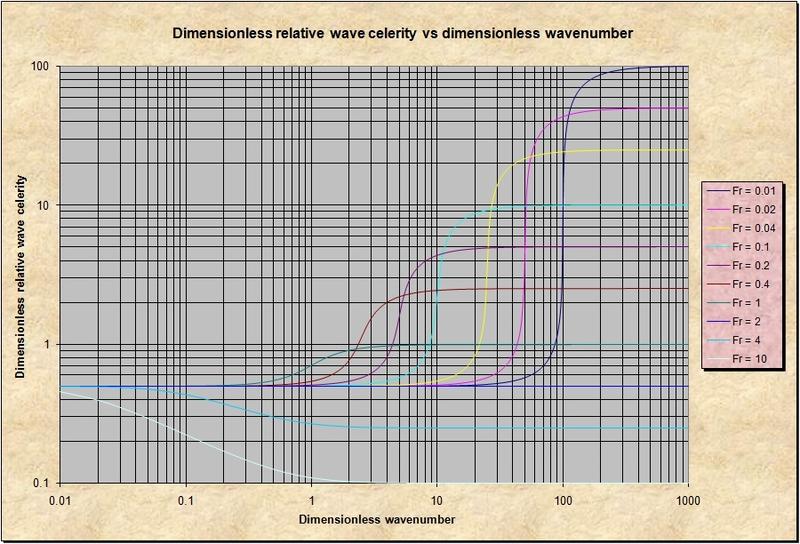

2. VISCOSITY NUMBERS
2.01
There are three viscosities in open-channel flow: 1. The microviscosity of the fluid, commonly referred to as the kinematic viscosity. 2. The macroviscosity of the steady flow, and 3. The wave viscosity, or viscosity of the unsteady flow.
2.02
The kinematic viscosity is commonly referred to as nu (ν), which varies as a function of temperature.
2.03
The macroviscosity of the steady flow is the product of the mean velocity times a characteristic length.
2.04
In closed-conduit flow, the characteristic length is the hydraulic radius, defined as follows:
2.05

      A
R =

      P

2.06
in which A = flow area, and P = wetted perimeter.
2.07
Thus, in closed-conduit flow, the macroviscosity is:
2.08

ν_M = v R

2.09
In open-channel flow, the characteristic length is the channel length L_o that it would take the steady equilibrium flow to drop a head equal to its depth h_o:
2.10

       h_o
L_o =

       S_o

2.11
in which S_o is the bed slope.
2.12
Thus, in open-channel flow, the macroviscosity of the steady flow is:
2.13

ν_M = v L_o

2.14
The wave viscosity is the product of the mean velocity times the wavelength of the unsteady disturbance.
2.15

ν_w = v L

2.16
in which L = wavelength of the disturbance.
2.17
The three viscosities give rise to two independent viscosity ratios.
2.18
These ratios are referred to as the Reynolds number and the dimensionless wavenumber.
2.19
The Reynolds number is the ratio of macroviscosity to microviscosity:
2.20

      v R
R_e =

       ν

2.21
Values of Reynolds number less than 500 describe laminar flow.
2.22
Values of Reynolds number greater than 2000 describe turbulent flow.
2.23
Values of Reynolds number in the range 500-2000 describe transitional flow.
2.24
The second viscosity ratio is the dimensionless wavenumber.
2.25
The dimensionless wave number is the ratio of macroviscosity to wave viscosity, affected with the factor 2 pi.
2.26

          L_o
σ_* = 2 π

          L

2.27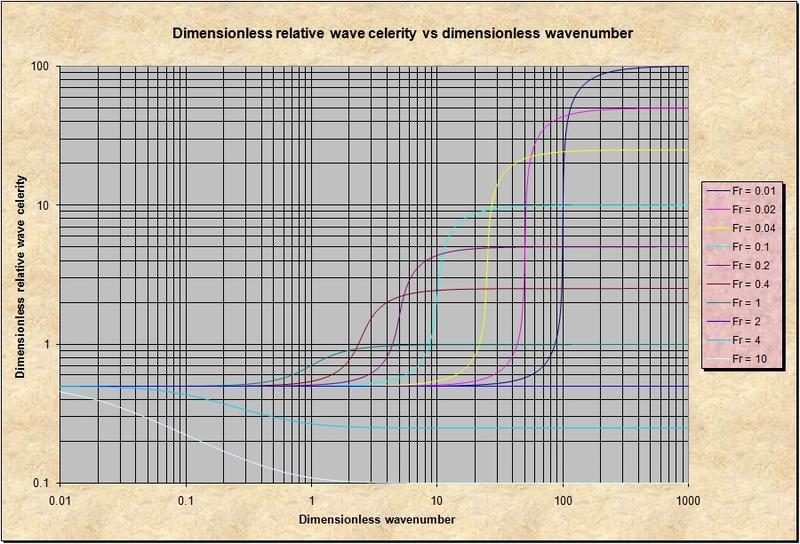

2.28
This figure shows the variation of dimensionless relative wave celerity vs dimensionless wavenumber.
2.29
Values of dimensionless wave number less than 1 describe kinematic flow, where frictional and gravitational forces predominate.
2.30
Values of dimensionless wave number greater than 100 describe dynamic flow, where inertial and pressure-gradient forces predominate.
2.31
Values of dimensionless wavenumbers in the range 1-100 describe mixed flow, where all four forces, gravity, friction, inertia, and pressure gradient, interact.
2.32
In practice, this mixed kinematic-dynamic flow is often referred to as dynamic wave, at the risk of confusion with the true dynamic wave flow, which follows the dynamic wave celerity.
2.33
In summary, the Froude number describes the direction of flow of primary surface waves, either upstream or downstream.
2.34
The Vedernikov number describes the external stability of the flow, either attenuating or amplifying.
2.35
The Reynolds number describes the state of internal stability of the flow, either laminar or turbulent.
2.36
The dimensionless wavenumber describes the predominance of either mass, in kinematic flow, or energy, in dynamic flow.
2.37
The celerity of kinematic waves follows the Seddon formula.
2.38
The celerity of dynamic waves follows the Lagrange formula.
2.39
The mixed waves lie in the middle of the spectrum, for which there no characteristic celerity.
2.40
Thus, unlike waves on both extremes of the spectrum, mixed waves are very strongly dissipative.
3.00

3.01

3.02

Narrator: Victor M. Ponce
Music: Fernando Oñate
Editor: Flor Pérez

Copyright © 2011
Visualab Productions
All rights reserved