OPEN-CHANNEL HYDRAULICS: LECTURE 032 - MOMENTUM PRINCIPLE

1. MOMENTUM PRINCIPLE
1.01
Energy is a scalar:

E = ∫ F dx

Eq. 1

1.02
Momentum is a vector:

M = ∫ F dt

Eq. 2

1.03
Kinetic energy is:

                    1
Kinetic Energy =
m v²
                    2
Eq. 3

1.04
Momentum is:

M = m v

Eq. 4

1.05
The mass flux is:

Mass flux = ρ Q

Eq. 5

1.06
in which ρ is the mass density of water and Q is the discharge.

1.07
The momentum flux, or force, is the mass flux times the velocity.

F = ρ Q v

Eq. 6

1.08
In general, the momentum flux is:

F = β ρ Q v

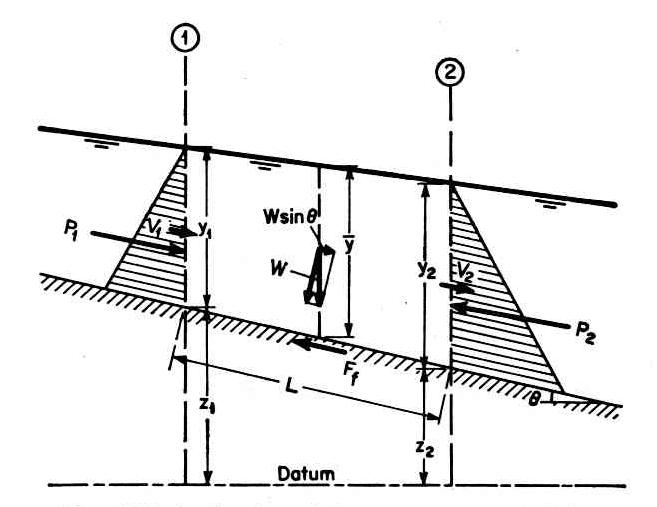
Eq. 7

1.09
There are four forces acting on a control volume: (1) gravitational, (2) frictional, (3) the force due to the pressure or depth gradient, and (4) inertial.
1.10
The gravitational force arises due to the nonzero bottom slope of typical open channels.
1.11
The frictional force arises due to the nonzero boundary friction in open channels in nature.
1.12
The pressure-gradient force arises due to the depth difference between usptream and downstream cross sections, under gradually varied flow.
1.13
The inertia force arises due to the dynamics of the flow. The imbalance between the other three forces produces a balancing inertia force.

2. MOMENTUM BALANCE
2.01
According to Newton's Second Law, the rate of change of momentum, that is, the momentum flux, or inertia force, is equal to the sum of all the external forces acting on the control volume.
2.02
The external surface forces are friction and the pressure gradient.
2.03
The external body force is gravity.
2.04
The statement of Newton's Second Law is:

ρ Q (β₂v₂ - β₁v₁) = P₁ - P₂ + W sin θ - F_f

Eq. 8

2.05
in which all external forces are shown here.
Fig. 01

External forces in a control volume.

2.06
The pressure forces in a hydraulically wide channel of width b are:

       1
P₁ =
γ y₁ (b y₁)
       2
Eq. 9

       1
P₂ =
γ y₂ (b y₂)
       2
Eq. 10

2.07
in which γ is the unit weight of water.

2.08
The average flow depth in the control volume is:

      1
y =
(y₁ + y₂)
      2
Eq. 11

2.09
The gravitational force along the direction of motion is:

F_g = W sin θ

Eq. 12

2.10
in which W is the weight of the water in the control volume.

2.11
Thus, the gravitational force is:

                 z₁ - z₂
F_g = (γ b y L)

                    L

Eq. 13

F_g = γ b y (z₁ - z₂)

Eq. 14

2.12
The frictional force is similar to the gravitational force, but with a friction head loss instead:

                 h_f'
F_f = (γ b y L)

                  L

Eq. 15

F_f = γ b y h_f'

Eq. 16

2.13
in which h_f' is the friction head loss.

2.14
The substitution of all external forces into the statement of conservation of momentum leads to:

              v₁²                 v₂²
z₁ + y₁ + β₁
= z₂ + y₂ + β₂
+ h_f'
              2g                  2g

Eq. 17

2.15
This equation is similar to the energy equation, but with momentum coefficients and friction loss.
2.16
The energy equation measures internal losses; the momentum equation measures external losses.
2.17
The losses have a tendency to be equal.

3. SPECIFIC FORCE
3.01
The concept of specific force is useful in certain applications of open-channel hydraulics.
3.02
Specific force arises from the application of the momentum principle to a short horizontal channel reach in a prismatic channel.
3.03
If the reach is short, friction can be neglected.
3.04
If the reach is horizontal, gravity can be neglected.
3.05
For simplicity, the momentum coefficient beta can be assumed to be equal to 1.
3.06
Thus, the momentum flux is balanced by the pressure gradient force only.

ρ Q (v₂ - v₁) = P₁ - P₂

Eq. 18

3.07
The pressure forces are:

P₁ = γ z₁ A₁

Eq. 19

P₂ = γ z₂ A₂

Eq. 20

3.08
in which z₁_bar and z₂_bar are the vertical distances measured from the water surface to the centroids of the flow areas A₁ and A₂, respectively.
3.09
The velocities are:

       Q
v₁ =

       A₁

Eq. 21

       Q
v₂ =

       A₂

Eq. 22

3.10
Thus, the momentum balance is:

       Q     Q
ρ Q (
-
) = γ z₁ A₁ - γ z₂ A₂
       A₂    A₁

Eq. 23

3.11
Rearranging and dividing by gamma:

   Q²               Q²

+ z₁ A₁ =
+ z₂ A₂ = constant
  g A₁             g A₂
Eq. 24

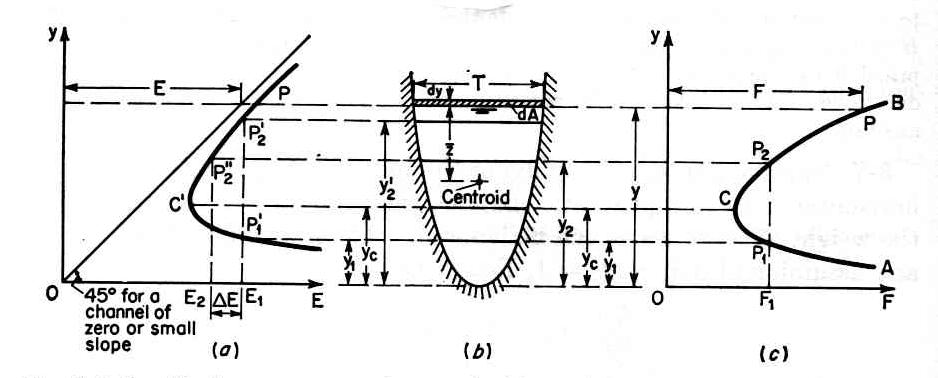
3.12
Therefore, the specific force F is constant in a short horizontal prismatic channel.

       Q²
F =
+ z A
      g A

Eq. 25

3.13
The units of specific force are force per weight per unit of volume, that is, volume units.
3.14
The specific force curve is a type of hyperbola, similar to the specific energy curve, with a minimum value of specific force corresponding to critical depth.
Fig. 02

Specific force and specific energy curves.

3.15
The minimum specific force is obtained by taking the derivative of specific force and equating to zero:

  dF        Q²  dA     d(zA)

= -

+
= 0
  dy       gA²  dy      dy

Eq. 26

3.16
The change in static moment of the flow area about the free surface is:

d(zA) = [A (z + dy) + T dy (dy/2)] - zA

Eq. 27

3.17
Neglecting the second-order term:

d(zA) = A dy

Eq. 28

  d(zA)

= A
   dy

Eq. 29

3.18
By definition, the top width is:

      dA
T =

      dy

Eq. 30

3.19
Substituting the top width and the derivative of the static moment into the statement of minimum specific force:

  Q² T

= 1
  g A³

Eq. 31

  v²

= 1
  gD

Eq. 32

3.20
Thus, under minimum specific force, the Froude number is equal to 1, that is, the flow is critical.

  F² = 1

Eq. 33

  F = 1

Eq. 34

3.21
For a hydraulically wide channel of width b, the specific force is:

      q²b²     y
F =
+
by
      gby     2
Eq. 35

      q²b     by²
F =
+

      gy      2
Eq. 36

3.22
For a hydraulically wide channel, the specific force per unit of channel width, in area units, is:

  F     q²     y²

=
+

  b     gy     2

Eq. 37

  F     v²y     y²

=
+

  b      g      2

Eq. 38

3.23
In units of force, the specific force is:

       γ Q²
γF =
+ γ z A
       g A

Eq. 39

       γq²b     γby²
γF =
+

        gy       2

Eq. 40

3.24
For a hydraulically wide channel, the specific force per unit of channel width, in units of force per width, is:

  γF     γq²     γy²

=
+

  b      gy      2

Eq. 41

  γF     γv²y     γy²

=
+

  b       g       2

Eq. 42

3.25
The specific force formulas are used to calculate the forces acting in short channel reaches.

Fig. 01

External forces in a control volume.

Fig. 02

Specific force and specific energy curves.

Fig. 03

Hydraulic jump in Tinajones outlet canal, Lambayeque, Peru.

Narrator: Victor M. Ponce
Music: Fernando Oñate
Editor: Flor Pérez

Copyright © 2011
Visualab Productions
All rights reserved