OPEN-CHANNEL HYDRAULICS: LECTURE 041 - CRITICAL FLOW

1. CRITICAL FLOW
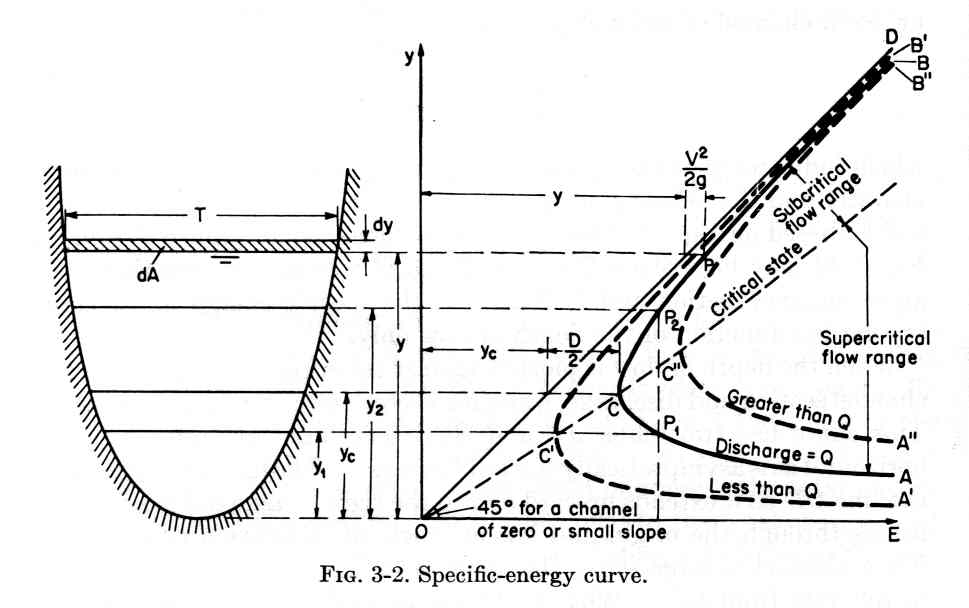
1.01
The following flow conditions characterize critical flow:
1. The specific energy is a minimum for a given discharge.
Fig. 01

Specific energy curve.

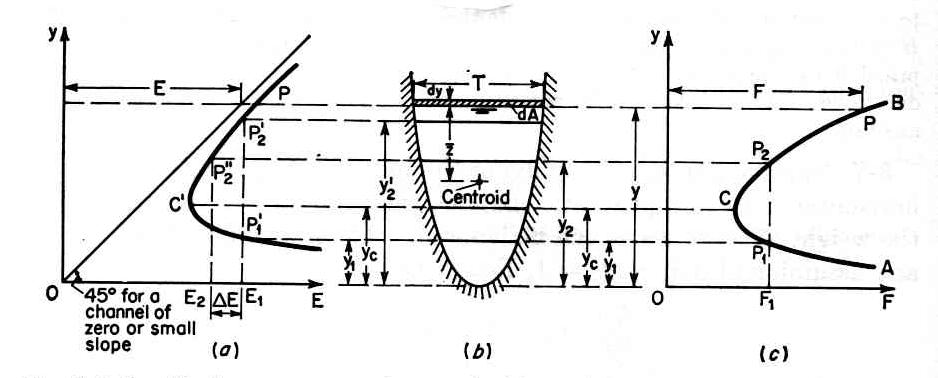
2. Discharge is a maximum for a given specific energy.
3. The specific force is a minimum for a given discharge.
Fig. 02

Specific force curve.

4. Discharge is a maximum for a given specific force.
5. The velocity head is equal to half of the hydraulic depth.

  v²     D

=

  2g     2

Eq. 1

6. The mean velocity is equal to the relative celerity of dynamic waves.

v = (gD)^1/2

Eq. 2

7. The Froude number is equal to 1.

         v
F =
= 1
      (gD)^1/2

Eq. 3

1.02
The celerity of dynamic waves is:

c_d = v +- (gD)^1/2

Eq. 4

1.03
The celerity of dynamic waves, relative to the flow, is:

c_d,r = +- (gD)^1/2

Eq. 5

1.04
Positive waves move with the flow; they are primary waves.
1.05
Negative waves move against the flow; they are secondary waves.

1.06
Under critical flow, secondary waves remain stationary.
Fig. 03

Control under critical flow.

1.07
Under subcritical flow, secondary waves are able to move upstream.

1.08
Under supercritical flow, secondary waves can only move downstream.

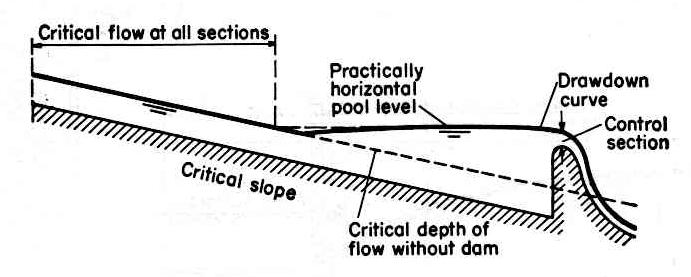
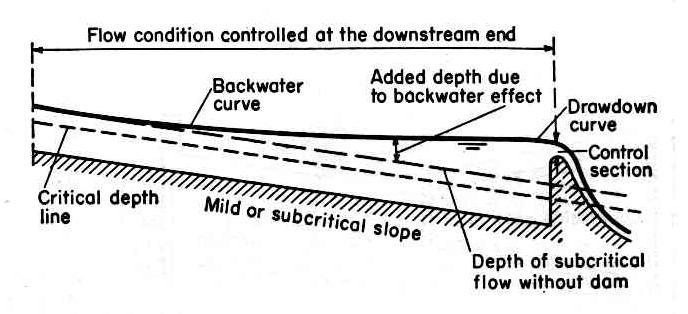
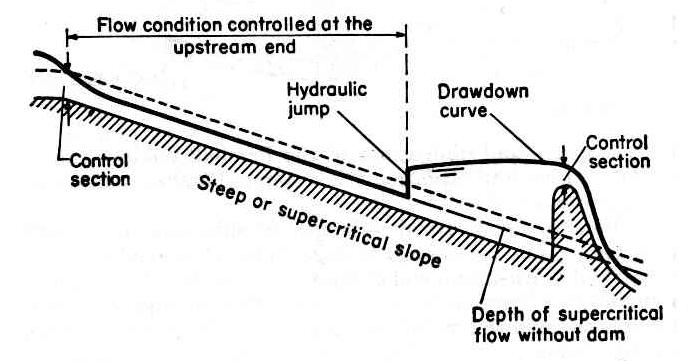
1.09
Subcritical flow is controlled from a downstream section, since secondary surface waves are able to move upstream.
Fig. 04

Control under subcritical flow.

1.10
Supercritical flow is controlled from an upstream section only, since secondary surface waves are not able to move upstream.
Fig. 05

Control under supercritical flow.

1.11
Critical depth can occur in two modes:
1. Along the channel, in uniform flow, and
2. At a cross section, in either gradually or rapidly varied flow.

1.12
A channel where critical depth occurs throughout its length is a critical channel.
Fig. 06

Canal operating near critical flow.

1.13
The slope of the critical channel is the critical slope S_c.

1.14
The cross section where critical flow occurs is the critical cross section.
Fig. 07

Critical cross section at a canal drop.

1.15
The friction relation for uniform flow in a hydraulically wide channel is:

S_o = f F²

Eq. 6

1.16
in which S_o is the bottom slope, or bed slope, and f is an open-channel friction factor equal to 1/8 of the Darcy-Weisbach friction factor.

1.17
Under critical flow, the Froude number is equal to 1. Thus, the friction equation reduces to:

S_o = f = S_c

Eq. 7

1.18
In other words, the friction factor and the critical slope are one and the same.

1.19
For applications to gradually varied flow, it is convenient to recast the friction relation as:

S_o = S_c F²

Eq. 8

1.20
In natural channels, critical flow appears to be a self-regulating upper limit to the Froude number.
1.21
This is because as friction increases due to bedform roughness, the Froude number cannot continue to increase and still satisfy the friction equation.

1.22
In artificial channels, with no bedform roughness, supercritical flow is possible.
Fig. 09

Supercritical flow on spillway at Turner Dam, San Diego County, California.

2. COMPUTATION
2.01
Under critical flow, the Froude number is equal to 1.

         v
F =
= 1
      (gD)^1/2

Eq. 9

2.02
For computational convenience, we square the Froude number.

       v²
F² =
= 1
       gD

Eq. 10

2.03
From continuity v = Q/A, and hydraulic depth D = A/T:

  Q² T

= 1
  g A³

Eq. 11

2.04
This equation can be expressed as:

  Q²

T - A³ = 0
  g

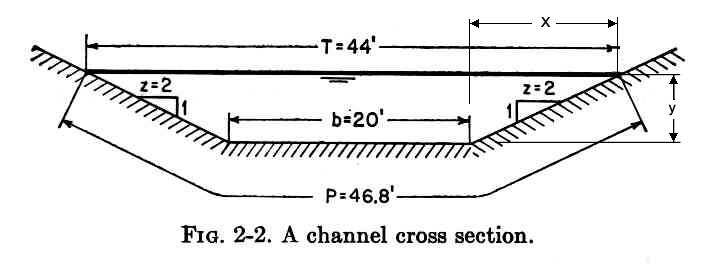
Eq. 12

2.05
In a typical prismatic channel, the input hydraulic variables for critical flow are:
1. Discharge Q,
2. Bottom width b, and
3. Side slope z: z horizontal to 1 vertical

Fig. 08

A typical prismatic channel cross section.

2.06
For b different than zero, and z different than zero, the channel is trapezoidal.
2.07
For z = 0, the channel is rectangular.
2.08
For b = 0, the channel is triangular.
2.09
The top width is:

T = b + 2x = b + 2zy

Eq. 13

2.10
The flow area is:

A = (1/2)(b + T)y = (b + zy)y

Eq. 14

2.11
Substituting into the critical flow equation:

  Q²

(b + 2zy_c) - [(b + zy_c)y_c]³ = 0
  g

Eq. 15

2.12
Given the input variables Q, b, and z, this equation is solved for the critical flow depth by iteration.

Fig. 01

Specific energy curve.

Fig. 02

Specific force curve.

Fig. 03

Control under critical flow.

Fig. 04

Control under subcritical flow.

Fig. 05

Control under supercritical flow.

Fig. 06

Canal operating near critical flow.

Fig. 07

Critical cross section at a canal drop.

Fig. 08

A typical prismatic channel cross section.

Fig. 09

Supercritical flow on spillway at Turner Dam, San Diego County, California.

Narrator: Victor M. Ponce
Music: Fernando Oñate
Editor: Flor Pérez

Copyright © 2011
Visualab Productions
All rights reserved