OPEN-CHANNEL HYDRAULICS:  LECTURE 051 - UNIFORM FLOW

1. UNIFORM FLOW
1.01
Uniform flow occurs in an artificial prismatic channel.
1.02
In uniform flow, the depth, area, mean velocity, and discharge are constant.

Fig. 01

Wellton-Mohawk Main Canal, Wellton, Arizona.

1.03
In uniform flow, the friction, energy, water-surface, and bottom or bed slope are the same.


 Sf = Se = Sw = So = S 

Eq. 1

1.04
In natural channels, steady equilibrium flow closely resembles the uniform flow of an artificial prismatic channel.
1.05
Under steady equilibrium flow, the average bottom slope is equal to the energy slope.
1.06
There is no unsteady uniform flow; if the flow is unsteady, it is not uniform.
1.07
However, for steep slopes, the flow may become unstable and unsteady.
1.08
The instability leads to the formation of roll waves, characterized by a train of small surface waves moving downstream.

Fig. 02

Roll waves on the spillway, Turner reservoir, San Diego County, California.

1.09
The Vedernikov number controls the formation of roll waves.


      (β -1)v
 V = 
 
       (gD)1/2


Eq. 2

1.10
in which β = exponent of the discharge-area rating, v = mean velocity, D = hydraulic depth, and g = gravitational acceleration.
1.11
At Vedernikov numbers less than 1, roll waves do not form, and uniform flow prevails.
1.12
At Vedernikov numbers greater than 1, roll waves do form, and uniform flow does not prevail.

Fig. 03

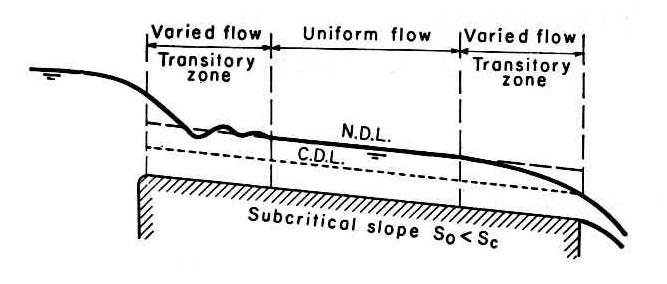
Roll waves in lateral canal, Cabana-Manazo irrigation project, Puno, Peru.

2. ESTABLISHMENT OF UNIFORM FLOW

2.01
Uniform flow is strictly a balance of gravitational and frictional forces.
2.02
Inertial and pressure-gradient forces do not participate in the description of uniform flow.
2.03
Therefore, uniform flow occurs when inertial and pressure-gradient forces are zero.
2.04
Mother Nature has a tendency to return to uniform or equilibrium flow.
2.05
The depth of uniform flow is called "normal depth."
2.06
When the bottom slope is less than the critical slope, the normal depth is greater than the critical depth, and the flow is termed "subcritical."

Fig. 04

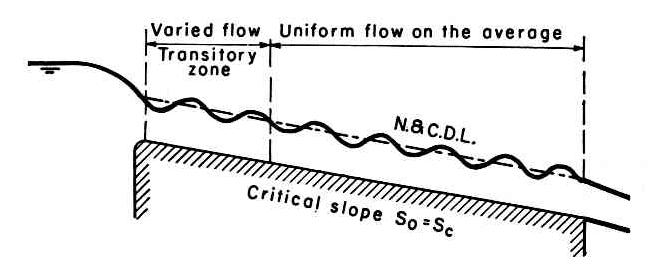
Establishment of uniform flow in a subcritical slope.

2.07
When the bottom slope is equal to the critical slope, the normal depth is equal to the critical depth, and the flow is termed "critical."

Fig. 05

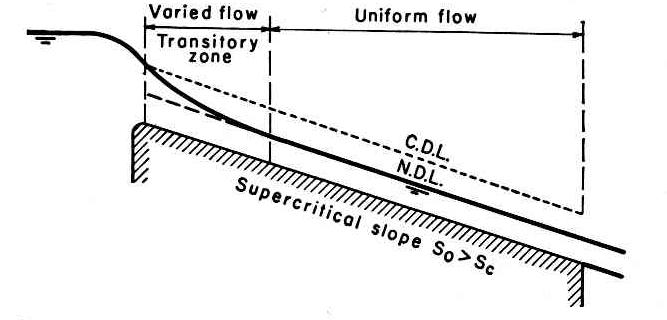
Establishment of uniform flow in a critical slope.

2.08
When the bottom slope is greater than the critical slope, the normal depth is smaller than the critical depth, and the flow is termed "supercritical."

Fig. 06

Establishment of uniform flow in a supercritical slope.

2.09
In general, the velocity of uniform flow is:


 v = C Rx Sy 

Eq. 3

2.10
in which C is a friction coefficient, R is the hydraulic radius, S is the friction slope, and x and y are exponents that vary with type of friction and cross-sectional shape.

Fig. 07

Tinajones feeder canal, Lambayeque, Peru.

Fig. 01

Wellton-Mohawk Main Canal, Wellton, Arizona.

Fig. 02

Roll waves on the spillway, Turner reservoir, San Diego County, California.

Fig. 03

Roll waves in lateral canal, Cabana-Manazo irrigation project, Puno, Peru.

Fig. 04

Establishment of uniform flow in a subcritical slope.

Fig. 05

Establishment of uniform flow in a critical slope.

Fig. 06

Establishment of uniform flow in a supercritical slope.

Fig. 07

Tinajones feeder canal, Lambayeque, Peru.

Narrator: Victor M. Ponce

Music: Fernando Oñate

Editor: Flor Pérez

Copyright © 2011

Visualab Productions

All rights reserved