OPEN-CHANNEL HYDRAULICS: LECTURE 055 - UNIFORM SURFACE FLOW

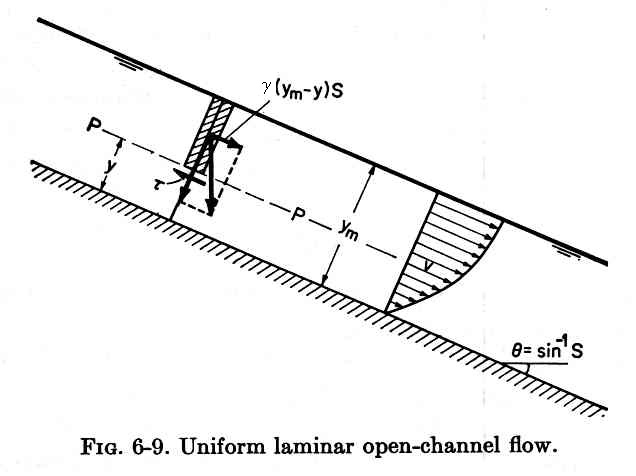
1. THEORY
1.01
Uniform overland flow is referred to as uniform surface flow.
1.02
In uniform surface flow, the depth is very small compared to the width.
1.03
This type of flow is also referred to as sheet flow.
1.04
The flow regime may be laminar, transitional, or turbulent.
1.05
If the depth is small, viscosity predominates and the flow is laminar.
1.06
The acting shear stress at level P at a distance y from the bottom is:

τ_a = γ (y_m - y) S

Eq. 1

Fig. 01

Definition sketch for laminar uniform surface flow.

1.07
where γ is the unit weight of water, y_m is the flow depth, and S is the bottom slope.
1.08
According to Newton's law of viscosity, the resisting shear stress at level P is:

        dv
τ_r = μ

        dy

Eq. 2

1.09
where μ is the dynamic viscosity. For equilibrium:

    dv
μ
= γ (y_m - y) S
    dy

Eq. 3

1.10
The velocity differential is:

dv = (γ/μ) (y_m - y) S dy

Eq. 4

1.11
The fluid properties are related as:

γ = ρ g

Eq. 5

μ = ρ ν

Eq. 6

1.12
Therefore:

dv = (gS/ν) (y_m - y) dy

Eq. 7

1.13
Integrating:

v = ∫ (gS/ν) (y_m - y) dy

Eq. 8

v = (gS/ν) [(y_my) - (y²/2)] + C

Eq. 9

1.14
For y = 0, v = 0. Therefore, the constant of integration is equal to 0.

1.15
The velocity distribution for laminar uniform surface flow is:

v = (gS/ν) [(y_my) - (y²/2)]

Eq. 10

1.16
The distribution is parabolic. The discharge rating is:

q = ∫ v dy

Eq. 11

q = (gS/ν) ∫ [(y_my) - (y²/2)] dy

Eq. 12

1.17
The integration between the limits y = 0 and y = y_m yields:

q = (gS/ν) [(y_m³/2) - (y_m³/6)]

Eq. 13

q = (gS/ν) (y_m³/3)

Eq. 14

q = [(gS)/(3ν)] y_m³ = C_L y_m³

Eq. 15

1.18
where C_L is the coefficient of the laminar surface flow rating:

       g S
C_L =

       3 ν

Eq. 16

1.19
Note that in laminar flow, the exponent of the rating is 3, and the rating is a function of the kinematic viscosity.

1.20
The mean velocity of laminar flow is:

v = q/y_m = C_L y_m²

Eq. 17

2. FLOW REGIMES

2.01
The rating for turbulent Manning uniform surface flow is:

q = v y_m = (1/n) S^1/2 y_m^5/3

Eq. 18

2.02
For turbulent Manning flow, the exponent of the rating is 5/3.

2.03
The rating for turbulent Chezy uniform surface flow is:

q = v y_m = C S^1/2 y_m^3/2

Eq. 19

2.04
For turbulent Chezy flow, the exponent of the rating is 3/2.

2.05
In uniform surface flow, the exponent of the rating varies from 3 for laminar flow, to 3/2 to 5/3 for turbulent flow, either Chezy or Manning, respectively.

2.06
Values of the rating exponent in between 3/2 or 5/3 and 3 correspond to a transitional flow regime.

2.07
Under gradually varied flow, surface flow may be laminar in some places and turbulent in others.

2.08
This type of flow is referred to as mixed laminar-turbulent flow regime, with values of the rating exponent similar to that of the transitional flow regime.

2.09
The Vedernikov number is:

      (β - 1) v
V =

        (gy_m)^1/2

Eq. 20

2.10
where β is the exponent of the rating.

2.11
In terms of Froude number:

V = (β - 1) F

Eq. 21

2.12
For Vedernikov number equal to 1, the Froude number is the neutrally stable Froude number, below which disturbances attenuate and above which disturbances amplify.

          1
F_ns =

        β - 1

Eq. 22

2.13
This table shows neutrally stable Froude numbers as a function of flow regime and corresponding rating exponent.

Flow regime β F_ns

Laminar 3 1/2

Turbulent Manning 5/3 3/2

Turbulent Chezy 3/2 2

2.14
It is seen that while the neutrally stable Froude number is 2 for turbulent Chezy flow, it is only 0.5 for laminar flow.

2.15
This means that surface instabilities may develop under laminar surface flow for values of Froude number well below critical.

Fig. 01

Definition sketch for laminar uniform surface flow.

Narrator: Victor M. Ponce
Music: Fernando Oñate
Editor: Flor Pérez

Copyright © 2011
Visualab Productions
All rights reserved