OPEN-CHANNEL HYDRAULICS:  LECTURE 071 - GRADUALLY VARIED FLOW

1. DEFINITION

1.01
Gradually varied flow is very common in practice.
1.02
It is the foundation for the calculation of water surface profiles used in analysis and design.
1.03
In general, gradually varied flow can be steady or unsteady.
1.04
Normally, however, the term "gradually varied flow" is used to refer to steady gradually varied flow.
1.05
Unsteady gradually varied flow is referred to simply as unsteady flow.
1.06
In gradually varied flow, the following conditions are assumed:

1. The flow is steady.

2. The flow is parallel, as opposed to curvilinear.

3. The head loss can be approximated as that of uniform flow.

4. The roughness can be approximated as that of uniform flow.

5. The pressure correction factor cosθ can be approximated as 1.

6. Air entrainment is negligible.

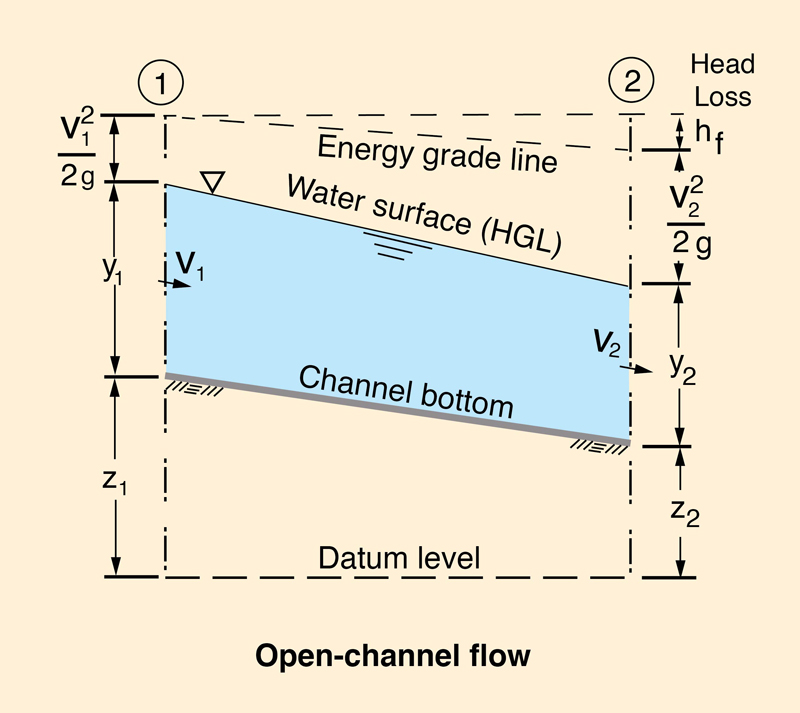
2. GOVERNING EQUATION

2.01
The gradient of hydraulic head is:


   dH     d             V2
 
 = 
 [z + y + 
] = - Sf 
   dx     dx            2g

Eq. 1

Fig. 01

Definition sketch for gradually varied flow.

2.02
The negative sign for the friction slope is needed because the flow is from left to right, while the derivative is taken from right to left by convention.

2.03
The friction slope is:


       hf
 Sf = 
 
       L

Eq. 2

2.04
where hf is the head loss due to friction, and L is the length of the channel reach.
2.05
The gradient of specific energy is:


   dE     d         V2         dz
 
 = 
 [y + 
] = - 
 - Sf 
   dx     dx        2g         dx

Eq. 3

2.06
The gradient of the channel bed, or bottom slope, is:


   dz      z2 - z1
 
 = 
 
   dx         L

Eq. 4


    dz      z1 - z2
 - 
 = 
 = So 
    dx         L

Eq. 5

2.07
Therefore, the gradient of specific energy is:


  d         V2
 
 [y + 
] =  So - Sf 
  dx        2g

Eq. 6

2.08
Under steady flow, the discharge Q = vA is constant. Replacing discharge in the gradient of specific energy:


  d          Q2
 
 [y + 
] =  So - Sf 
  dx        2gA2

Eq. 7

2.09
Operating on the derivatives:


  dy    d     Q2
 
 + 
 [
] =  So - Sf 
  dx    dx   2gA2

Eq. 8


  dy       Q2    dA
 
 - [
] 
 =  So - Sf 
  dx      gA3    dx

Eq. 9

2.10
Using the chain rule:


  dy       Q2    dA   dy
 
 - [
] 
 
 =  So - Sf 
  dx      gA3    dy   dx

Eq. 10

2.11
From the definition of top width T:


  dy      Q2T    dy
 
 - [
] 
 =  So - Sf 
  dx      gA3    dx

Eq. 11

2.12
Simplifying:


  dy        Q2T   
 
 [1 - 
] =  So - Sf 
  dx        gA3   

Eq. 12

2.13
From the definition of Froude number:


  dy           
 
 [1 - F2 ] =  So - Sf 
  dx           

Eq. 13

2.14
The dimensionless Chezy equation for hydraulically wide channels is:


 Sf = f F2 

Eq. 14

2.15
At critical flow, the friction slope is the critical slope. Therefore, the friction factor is equal to the critical slope.


 Sf = Sc F2 

Eq. 15

2.16
The gradually varied flow equation for hydraulically wide channels reduces to:


  dy           
 
 [1 - F2 ] =  So - Sc F2 
  dx           

Eq. 16


   dy      So - Sc F2
 
 = 
 
   dx        1 - F2

Eq. 17

2.17
Defining the depth gradient:


       dy
 Sy = 
 
       dx

Eq. 18

2.18
The final expression for the equation governing gradually varied flow in hydraulically wide channels is:


   Sy      (So/Sc) - F2
 
 = 
 
   Sc         1 - F2

Eq. 19

2.19
The only assumption of this equation is that of a hydraulically wide channel. The depth gradient is a only function of bottom slope, critical slope, and Froude number.

Fig. 01

Definition sketch for gradually varied flow.

Narrator: Victor M. Ponce

Music: Fernando Oñate

Editor: Flor Pérez

Copyright © 2011

Visualab Productions

All rights reserved