|
OPEN-CHANNEL HYDRAULICS: LECTURE 092 - THE HYDRAULIC JUMP
1. DESCRIPTION 1.01 The hydraulic jump occurs in open-channel flow when the flow changes from supercritical to subcritical, typically as a result of imposed downstream conditions. Fig. 10
1.02 The hydraulic jump always occurs with a loss of energy. Fig. 05
1.03 The hydraulic jump equations are strictly applicable to short horizontal channels, where the effects of gravity and friction are negligible. 1.04 The equations apply to channels of nonzero slope only as an approximation. 1.05 Practical applications of the hydraulic jump are the following: 1. To dissipate the energy of supercritical flow, as water goes over spillways and other rapidly varied flow conditions. Fig. 11
2. To recover hydraulic head for downstream use. 3. To increase the weight on a stilling basin and reduce uplift pressures. 4. To aerate water for water purification.
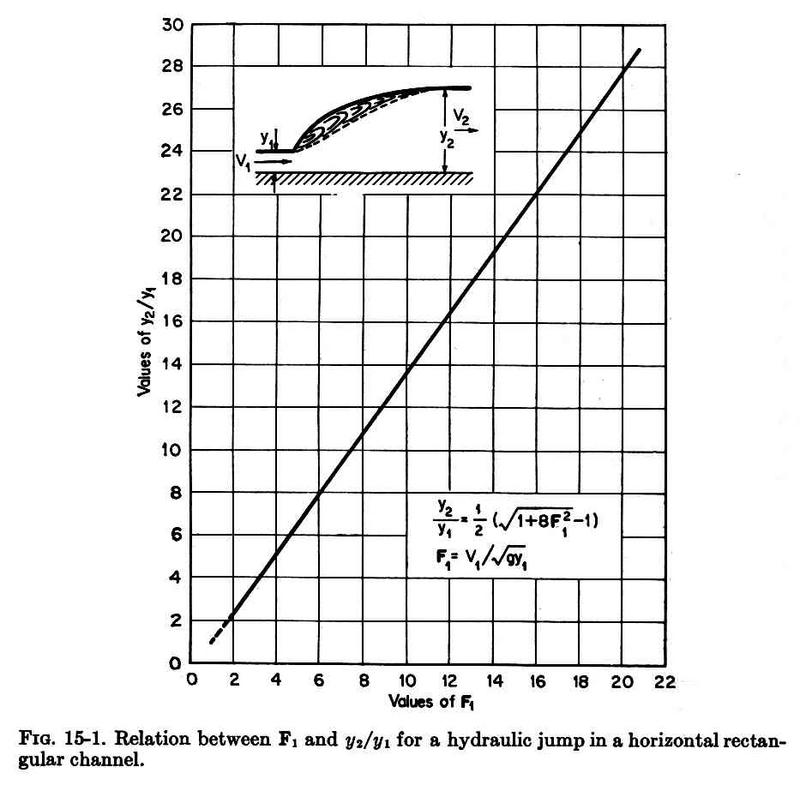
2. EQUATION 2.01 A hydraulic jump will form in an open channel if the upstream flow depth or initial depth y1, the downstream flow depth or sequent depth y2, and the Froude number of the upstream flow F1 satisfy the following equation:
Eq. 1
2.02 In other words, given supercritical upstream flow conditions, and having the hydraulic jump formed, the sequent depth y2 will follow the hydraulic jump equation. Fig. 12
2.03 The hydraulic jump equation is shown here in graphical form. Fig. 01
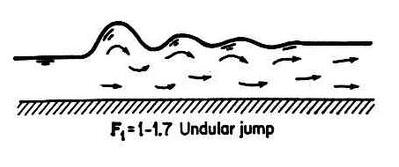
2.04 Note that the hydraulic jump will form for upstream Froude numbers in the range 1-22, and that the equation is almost linear through most of its practical range. 3. TYPES 3.01 According to the upstream Froude number, the hydraulic jump classifies into: 1. Undular jump: 1.0-1.7 Fig. 02
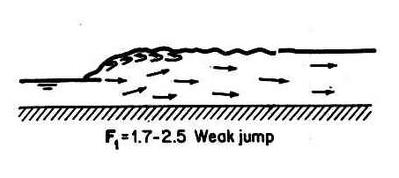
2. Weak jump: 1.7-2.5 Fig. 03
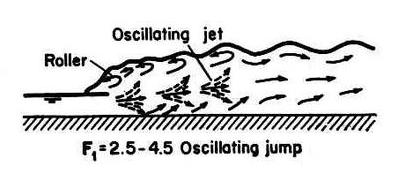
3. Oscillating jump: 2.5-4.5 Fig. 04
4. Steady jump: 4.5-9.0 Fig. 05
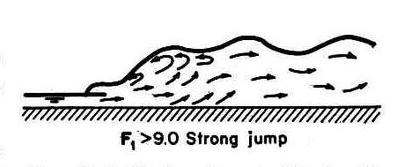
5. Strong jump: 9.0 and above. Fig. 06
Fig. 13
4. CHARACTERISTICS 4.01 The energy loss is the difference between the specific energy upstream and downstream of the jump.
Eq. 2 4.02 The efficiency of the hydraulic jump is the ratio of specific energies downstream and upstream of the jump.
Eq. 3 4.03 The relative energy loss of the jump is:
Eq. 4 4.04 The height of the jump is:
Eq. 5
4.05 The relative height of the jump is:
Eq. 6
4.06 The relative height of the jump can also be expressed as:
Eq. 7
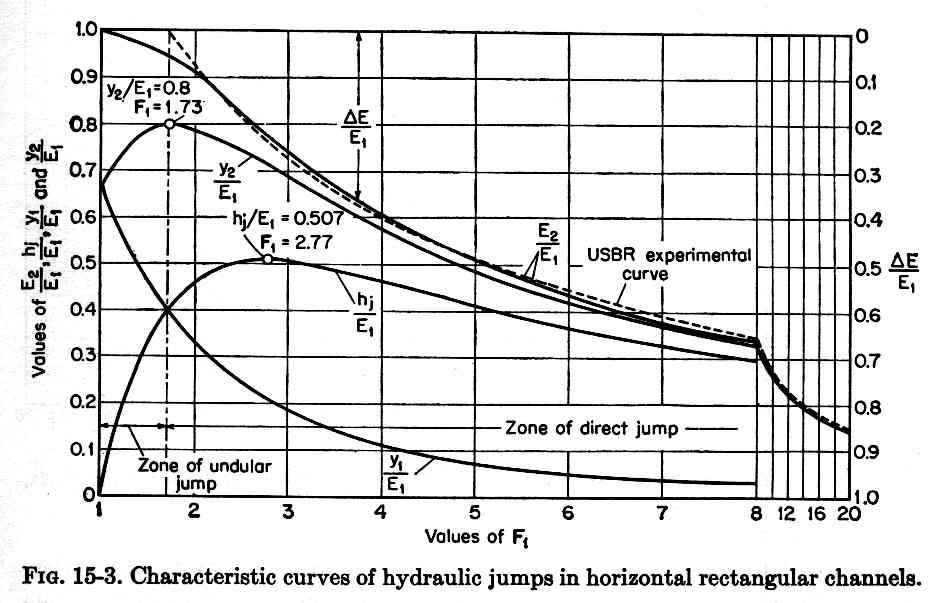
4.07 This figure shows a graphical portrayal of the hydraulic jump characteristics. Fig. 07
4.08 The maximum relative height hj/E1 is 0.507 at F1 = 2.77.
4.09 The maximum relative sequent depth y2/E1 is 0.8 at F1 = 1.73
4.10 Experiments shows that the transition from undular to weak jump occur at this value of upstream Froude number F1 = 1.73
4.11 For critical flow, F1 = 1, it is confirmed that y1/E1 = y2/E1 = 0.67 = 2/3
4.12 For F1 greater than 3, the changes in all characteristics are gradual and monotonic.
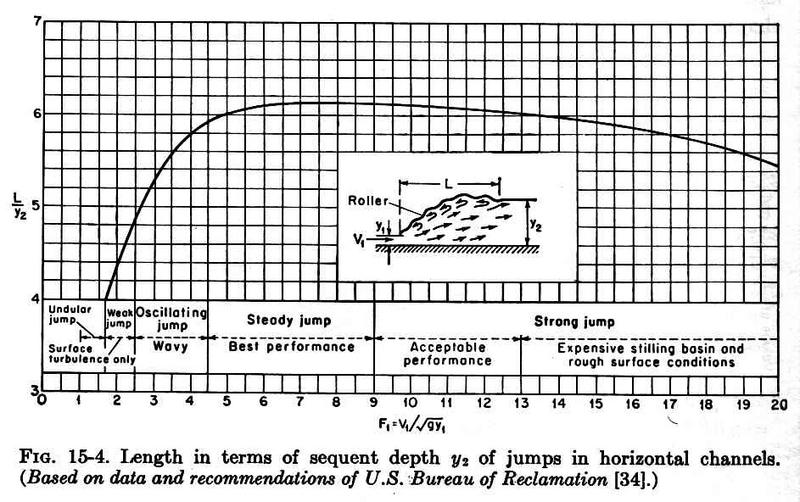
5. LENGTH 5.01 The length of the hydraulic jump is the distance from the front face of the jump to a point located immediately downstream of the roller. 5.02 The relative length of the jump is the ratio of the length L to the sequent depth y2. 5.03 This figure shows the relative length as a function of the upstream Froude number. Fig. 08
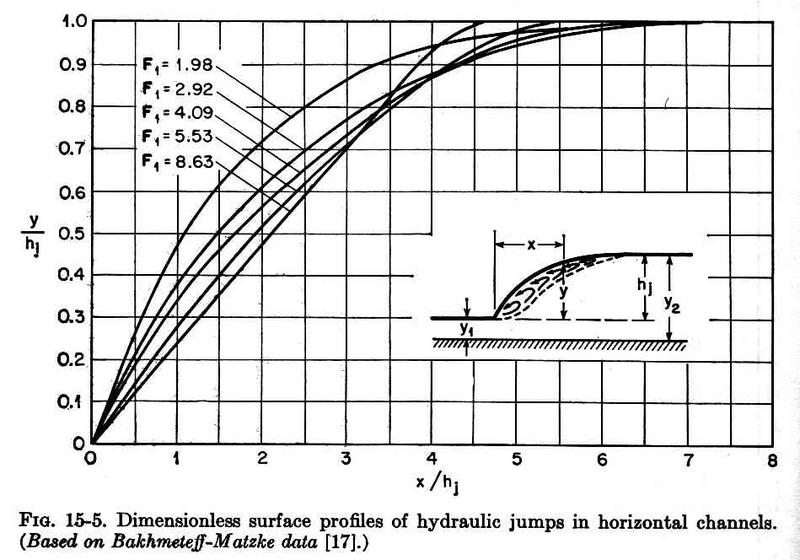
5.04 Note that the relative length of the jump varies between 4 and 6 for most jumps, peaking about 6 for the steady jump. 5.05 This figure shows dimensionless profiles of the hydraulic jump. Fig. 09
Fig. 01
Fig. 02
Fig. 03
Fig. 04
Fig. 05
Fig. 06
Fig. 07
Fig. 08
Fig. 09
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Narrator: Victor M. Ponce Music: Fernando Oñate Editor: Flor Pérez
Copyright © 2011 Visualab Productions All rights reserved
|