OPEN-CHANNEL HYDRAULICS: LECTURE 101 - UNSTEADY FLOW

1. THEORY
1.01
In general, there are four forces in open-channel flow, resolved along the direction of motion:
1. The gravitational force,
2. The frictional force along the channel bottom, opposite to the direction of motion,
3. The force arising from the existence of a pressure gradient, and
4. The inertia force.
1.02
When the inertia force is negligible compared to the other three, the flow is steady.
1.03
When the inertia and pressure gradient forces are negligible compared to the other two, the flow is uniform.
1.04
The flow is unsteady when all four forces are acting, and none can be neglected.
1.05
Unsteady flow is the most general type of open-channel flow.
1.06
Unsteady flow can be either gradually varied, or rapidly varied.
1.07
Unsteady gradually varied flow assumes parallel flow.
1.08
Therefore, it is an extension of steady gradually varied flow to the unsteady case.
1.09
The typical example of unsteady gradually varied flow is flood routing.
Fig. 01

Flood stage on the Chane river, Eastern Bolivia.

1.10
Floods are unsteady and gradually varied for the most part.
1.11
Unsteady rapidly varied flow assumes curvilinear flow.
1.12
Therefore, it is an extension of steady rapidly varied flow to the unsteady case.
1.13
A typical example of unsteady rapidly varied flow is the kinematic shock.
1.14
The kinematic shock is a kinematic wave that has become rapidly varied by steepening, to the point where it resembles, for all practical purposes, a wall of water.
1.15
Other examples of unsteady rapidly varied flow are surface waves, surges, tidal waves, and debris flows.
Fig. 05

Surface wave on the Hassayampa river, Arizona, February 2, 1993.

1.16
Most applications of unsteady flow are in flood routing; therefore, it is customary to refer to unsteady gradually varied flow simply as unsteady flow.

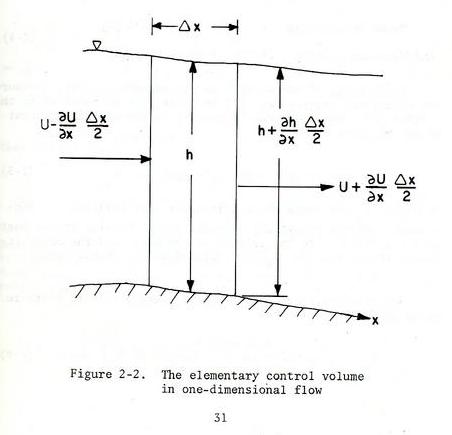
2. GOVERNING EQUATIONS
2.01
The governing equations of unsteady gradually varied flow arise from a statement of the principles of mass and momentum conservation in a control volume.
2.02
Assume a unit-width control volume, with velocity u and depth h.
Fig. 04

Definition sketch for variables in unit-width control volume.

2.03
The conservation of mass states that the difference between inflow and outflow is balanced by a change in storage volume.

            ∂U          ∂h        ∂h
uh - [u +
Δx][h +
Δx] =
Δx
            ∂x          ∂x        ∂t

Eq. 1

2.04
Simplifying:

  ∂h       ∂h       ∂u

+ u
+ h
= 0
  ∂t       ∂x       ∂x

Eq. 2

  ∂h     ∂

+
(uh) = 0
  ∂t     ∂x

Eq. 3

2.05
This is the statement of conservation of mass, commonly referred to as the water continuity equation.
2.06
The conservation of momentum states that the difference between momentum fluxes entering and leaving the control volume plus the sum of the forces acting is equal to the rate of change of momentum.
2.07
The Momentum flux entering the control volume is:

Mom. flux entering = ρu²h

Eq. 4

2.08
The momentum flux leaving the control volume is:

                              ∂
Mom. flux leaving = ρu²h +
(ρu²h) Δx
                              ∂x

Eq. 5

2.09
The hidrostatic pressure force upstream of the control volume is:

P₁ = (1/2)γh(h) = (1/2)ρgh²

Eq. 6

2.10
The hidrostatic pressure force downstream of the control volume is:

                        ∂
P₂ = - (1/2) ρg [h² +
(h²) Δx]
                        ∂x

Eq. 7

2.11
The gravitational force resolved along the direction of motion is:

F_g = ρgh Δx S_o

Eq. 8

2.12
where S_o is the bottom slope.
2.13
The frictional force acting along the bottom, opposite to the direction of motion is:

F_f = - ρgh Δx S_f

Eq. 9

2.14
where S_f is the friction slope.
2.15
The rate of change of momentum within the control volume is:

                                ∂
Rate of change of momentum =
(mu)
                                ∂t

Eq. 10

2.16
where m is the mass of the control volume.

                                ∂
Rate of change of momentum =
(ρuh) Δx
                                ∂t

Eq. 11

2.17
Summing up all the forces leads to:

  ∂         ∂               ∂

(uh) +
(u²h) + (g/2)
(h²) + gh(S_f - S_o) = 0
  ∂t        ∂x              ∂x
Eq. 12

2.18
This equation is in its conservation form. Often it is used in reduced form. The derivatives are operated to yield:

   ∂u      ∂h      ∂              ∂u       ∂h
h
+ u
+ u
(uh) + (uh)
+ gh
+ gh(S_f - S_o) = 0
   ∂t      ∂t      ∂x             ∂x       ∂x
Eq. 13

2.19
The second and third terms are recognized as the statement of conservation of mass; therefore, they cancel out. Dividing by flow depth h we obtain the equation of conservation of momentum in reduced form.

  ∂u      ∂u      ∂h

+ u
+ g
+ g(S_f - S_o) = 0
  ∂t      ∂x      ∂x
Eq. 14

2.20
This equation is referred to as the equation of motion. By dividing this equation by the gravitational acceleration g, it is further expressed in terms of slopes only.

  1  ∂u     u  ∂u    ∂h

+

+
+ S_f - S_o = 0
  g  ∂t     g  ∂x    ∂x
Eq. 15

2.22
The first term in this equation is the local inertia slope; the second term is the convective inertia slope; the third term is the pressure gradient slope; the fourth is the friction slope, and the fifth if the gravitational slope.
2.23
Finally, the equation of motion reduces to:

S_a + S_c + S_p + S_f - S_o = 0

Eq. 16

2.23
Under uniform flow, the local inertia, convective inertia, and pressure gradient slopes reduce to zero. The equation of motion reduces to:

S_f - S_o = 0

Eq. 17

2.23
Under gradually varied flow, the local and convective inertia slopes reduce to zero. The equation of motion reduces to:

S_p + S_f - S_o = 0

Eq. 18

2.24
The inertia slopes play an important role in unsteady flow.
2.25
The convective inertia arises because of the fixed frame of reference being used, wherein the flow moves across this frame of reference.
2.26
This fixed frame of reference is referred to as Eulerian frame, which is different from a Lagrangian frame, where the frame moves with the flow.
2.27
A formulation following a Lagrangian frame does not have convective inertia.

Fig. 01

Flood stage on the Chane river, Eastern Bolivia.

Fig. 02

Flood stage on the Chane river, Eastern Bolivia.

Fig. 03

Flood stage on the Chane river, Eastern Bolivia.

Fig. 04

Definition sketch for variables in unit-width control volume.

Fig. 05

Surface wave on the Hassayampa river, Arizona, February 9, 1993.

Narrator: Victor M. Ponce
Music: Fernando Oñate
Editor: Flor Pérez

Copyright © 2011
Visualab Productions
All rights reserved