|
OPEN-CHANNEL HYDRAULICS: LECTURE 102 - WAVE PROPAGATION
1. WAVE TYPES 1.01 Several types of waves are in common use in unsteady open-channel flow. 1.02 Waves are classified according to the importance of the various slopes in the equation of motion. 1.03 The equation of motion, in slope form, is:
Eq. 1
1.04 A kinematic wave is represented by the balance of friction and gravitational slopes only. All other slopes are neglected.
Eq. 2
1.05 A diffusion wave is represented by the balance of pressure gradient, friction and gravitational slopes. All other slopes are neglected.
Eq. 3
1.06 A mixed kinematic-dynamic wave is represented by the balance of all slopes. No slope is neglected in a mixed wave.
Eq. 4
1.07 A dynamic wave is represented by the balance of local inertia, convective inertia, and pressure gradient slopes. All other slopes are neglected.
Eq. 5
1.09 Since the late 1970s, the term 'dynamic wave' has come to be associated, by way of practice, with the use of the complete equation of motion, that is, with the mixed kinematic-dynamic wave.
1.09 To avoid confusion, we refer here to the wave arising from the balance of inertia and pressure gradient only, as dynamic wave, and to the complete wave as mixed wave.
2. CHARACTERISTICS 2.01 Kinematic waves travel with the kinematic wave celerity and are not subject to attenuation. 2.02 However, kinematic waves can undergo steepening or flattening depending on the interaction of the flow with the cross-sectional geometry. 2.03 If carried long enough, the steepening of kinematic waves can lead to a phenomenon referred to as the 'kinematic shock.' 2.04 The kinematic shock is a kinematic wave that has steepened to the point where the front face of the wave becomes, for all practical purposes, a wall of water. 2.05 The kinematic wave celerity, referred to as the Seddon celerity, is defined as the slope of the discharge-area rating:
Eq. 6 2.06 Since dA = T dy:
Eq. 7 2.07 Since the discharge-area rating is:
Eq. 8
2.08 the kinematic wave celerity is also expressed as:
Eq. 9
2.09 In general, β is greater than 1. Therefore, the kinematic wave celerity is greater than the velocity by the factor β.
2.10 The relative kinematic wave celerity, that is, the celerity relative to the flow, is:
Eq. 10
2.11 The dimensionless relative kinematic wave celerity, that is, the relative celerity divided by the velocity, is:
Eq. 11
2.12 The celerity of the diffusion wave can be approximated as that of the kinematic wave.
2.13 However, unlike the kinematic wave, the diffusion wave does have the capability to undergo attenuation.
2.14 The attenuation of the diffusion wave is due to the pressure gradient; the greater the pressure gradient, the greater the attenuation.
2.15 The dimensionless relative dynamic wave celerity is the reciprocal of the Froude number:
Eq. 12
Eq. 13
2.16 The relative dynamic wave celerity is:
Eq. 14
2.17 The dynamic wave celerity is:
Eq. 15
2.18 The equation is referred to as the Lagrange celerity equation.
2.19 Note that while the dimensionless relative kinematic wave celerity is a constant, and equal to β -1, the dimensionless relative dynamic wave celerity is the reciprocal of the Froude number. 3. LINEAR SOLUTION 3.01 The solution of the complete mixed kinematic-dynamic wave, or mixed wave, is possible by a linear stability analysis of the governing equations. 3.02 These are the equations of continuity and motion, referred to as collectively as the St. Venant equations.
Eq. 16
Eq. 17 3.03 The analysis leads to a solution for dimensionless relative wave celerity as a function of dimensionless wavenumber. 3.04 The dimensionless relative wave celerity is equal to the wave celerity minus the flow velocity, divided by the flow velocity.
Eq. 18
3.05 The dimensionless wavenumber is the wavenumber multiplied by a reference channel length Lo.
Eq. 19 3.06 The reference channel length is the channel length that it would take the steady equilibrium flow to drop a head equal to its depth.
Eq. 20
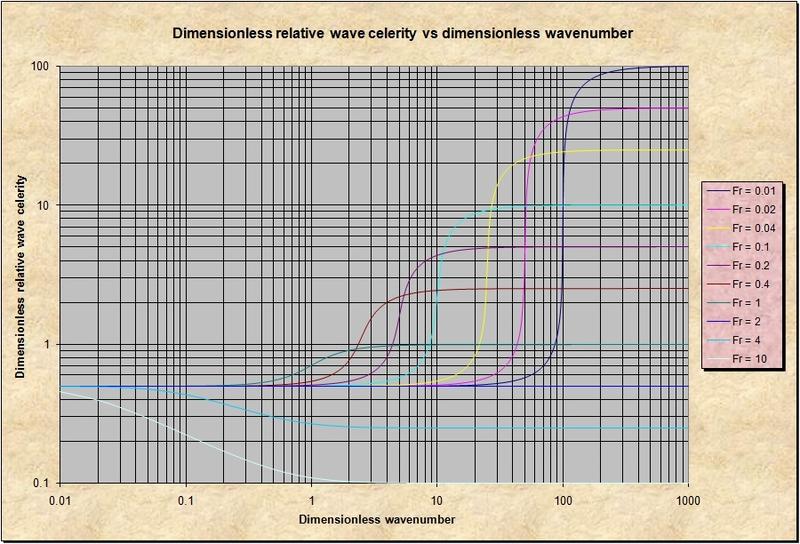
3.07 The function of dimensionless relative wave celerity vs dimensionless wavenumber for the practical range of Froude numbers between 0.01 and 10 is shown here. Fig. 01
3.08 We draw the following conclusions: 1. For dimensionless wavenumbers less than 1, and Froude numbers less than 2, the flow is essentially kinematic, being governed by the kinematic wave celerity. The dimensionless relative kinematic wave celerity is 0.5, applicable to Chezy friction in hydraulically wide channels. 2. For dimensionless wavenumbers greater than 100, the flow is essentially dynamic, being governed by the dynamic wave celerity. The dimensionless relative dynamic wave celerity is the reciprocal of the Froude number. 3. For dimensionless wavenumbers in the range 1-100, the flow is essentially mixed flow. There is no characteristic celerity for mixed flow.
3.09 Further analysis of this figure enable the following conclusions: 1. For Froude number equal 2, which for Chezy friction in hydraulically wide channels corresponds to Vedernikov number equal to 1, the dimensionless relative wave celerity is a constant, and equal to 0.5. This is the threshold for the formation of rolls waves in steep channels. 2. At both extremes of the dimensionless wavenumber spectrum, where kinematic and dynamic waves prevail, wave attenuation is zero. This corresponds with a constant dimensionless relative wave celerity. 3. In the middle of the spectrum, for mixed waves, wave attenuation is strong. Wave attenuation peaks at the point of inflection in the wavenumber spectrum. 4. Wave attenuation is extremely high at or near the point of inflection. We conclude that mixed waves are extremely dissipative. This is due to the lack of characteristic celerity, the actual celerity varying with wavenumber.
4. SUMMARY 4.01 This table summarizes celerity and attenuation properties of open-channel flow waves.
Fig. 01
Fig. 02
Narrator: Victor M. Ponce Music: Fernando Oñate Editor: Flor Pérez
Copyright © 2011 Visualab Productions All rights reserved
|