OPEN-CHANNEL HYDRAULICS: LECTURE 103 - FLOOD ROUTING

1. KINEMATIC WAVES
1.01
Flood routing is the process of calculating a flood, either for design, forecasting, or hindcasting purposes.
Fig. 01

Flood on the Chane river, Eastern Bolivia.

1.02
Flood routing can be applied to kinematic, diffusion, and mixed dynamic waves.
1.03
Routing with kinematic and diffusion waves is described here.
1.04
Kinematic waves are governed by the equation of water continuity and a simplified equation of motion that considers only gravitational and frictional forces.
1.05
The equation of water continuity is:

  ∂h    ∂

+
(uh) = 0
  ∂t    ∂x

Eq. 1

1.06
in which u = mean velocity, and h = flow depth.
1.07
In terms of discharge and flow area, the equation of water continuity is:

  ∂Q    ∂A

+
= 0
  ∂x    ∂t

Eq. 2

1.08
For kinematic waves, the equation of motion is:

S_f = S_o

Eq. 3

1.09
in which S_f is the friction slope and S_o is the bottom slope.
1.10
This equation can be expressed as a steady equilibrium rating:

Q = α A^β

Eq. 4

1.11
Taking the derivative:

  dQ                 Q

= α β A^β-1 = β
= β v = c
  dA                 A

Eq. 5

1.12
in which c is the kinematic wave celerity, or Seddon celerity.

1.13
Multiplying the kinematic wave celerity with the water continuity equation and applying the chain rule leads to the kinematic wave equation:

  ∂Q      ∂Q

+ c
= 0
  ∂t      ∂x

Eq. 6

1.14
Note that the kinematic wave equation is of first order; therefore, it can describe convection, but it cannot describe diffusion.

1.15
This fact has significant implications for flood routing.

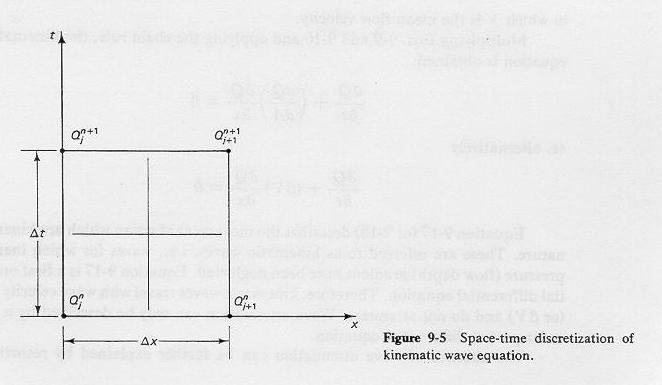
1.16
The numerical solution of the kinematic wave equation on a grid system is a function of the Courant number:

        Δt
C = c

        Δx

Eq. 7

1.17
in which Δx is the time interval, and Δt is the time interval.

1.18
There are many numerical schemes to solve the kinematic wave equation.

1.19
In practice, the forward-in-time/backward-in-space and forward-in-space/backward-in-time schemes remain the most common.

1.20
A combination of these two schemes is used in the Army Corps of Engineers' HEC-HMS hydrologic model.

1.21
Unfortunately, depending on the prevailing Courant number, these schemes introduce a certain amount of numerical diffusion and dispersion.

1.22
Numerical diffusion and dispersion arise in a numerical computation due to the finite size of the grid.

1.23
Numerical diffusion is a first-order error; numerical dispersion is a second-order error.

1.24
For kinematic wave schemes, the numerical diffusion is arbitrary and not related to the physical diffusion, if any, of the actual wave propagation problem.

1.25
Therefore, a numerical solution of the kinematic wave equation remains essentially a conceptual model, not necessarily related to the actual physics of the phenomena.

2. DIFFUSION WAVES
2.01
Diffusion waves are governed by the equation of water continuity and a simplified equation of motion that considers only gravitational, frictional, and pressure gradient forces.
2.02
For diffusion waves, the equation of motion is:

S_p + S_f - S_o = 0

Eq. 8

           dh
S_f = S_o -

           dx
Eq. 9

2.03
In the diffusion wave model, the pressure gradient term is responsible for the diffusion effect.

2.04
The combination of water continuity equation and equation of motion of diffusion waves leads to the diffusion wave equation:

  ∂Q      ∂Q       ∂²Q

+ c
= ν_h

  ∂t      ∂x       ∂x²

Eq. 10

2.05
in which ν_h is the hydraulic diffusivity, or Hayami diffusivity:

       q_o
ν_h =

       2S_o

Eq. 11

2.06
q_o is the reference unit-width discharge.

2.07
Note that the diffusion wave equation is of second order; therefore, it can describe physical diffusion, unlike the kinematic wave equation, which cannot.

2.08
We conclude that the kinematic wave can describe diffusion only by the introduction of numerical diffusion, while the diffusion wave can describe diffusion on its own, without the need to rely on numerical diffusion.

2.09
In practice, the diffusion wave equation is solved numerically using the Muskingum-Cunge method.

2.10
This method parallels the classical Muskingum method of flood routing.

2.11
However, unlike the Muskingum method, where the parameters are determined by calibration using measured data, in the Muskingum-Cunge method the parameters are estimated based on physical and numerical principles.

3. MUSKINGUM METHOD
3.01
The differential equation of storage is:

          dS
I - O =

          dt

Eq. 12

3.02
In the Muskingum method, the relation between inflow, outflow, and storage is:

S = K[XI + (1 - X)O]

Eq. 13

3.03
in which K and X are the Muskingum routing parameters.
3.04
The parameter K is a time of storage, and X is a dimensionless weighting factor.
3.05
The substitution of the Muskingum relation into the differential equation of storage leads to the routing equation:

Q_j+1ⁿ⁺¹ = C₀ Q_jⁿ⁺¹ + C₁ Q_jⁿ + C₂ Q_j+1ⁿ

Eq. 14

3.06
with the routing coefficients:

        (Δt/K) - 2X
C₀ =

      2(1-X) + (Δt/K)

Eq. 15

        (Δt/K) + 2X
C₁ =

      2(1-X) + (Δt/K)

Eq. 16

      2(1-X) - (Δt/K)
C₂ =

      2(1-X) + (Δt/K)

Eq. 17

3.07
The parameters K and X are obtained by calibration using measured data, that is, with stream gaging.

3.08
Therefore, the method is strictly applicable to gaged streams.

4. MUSKINGUM-CUNGE METHOD
4.01
The Muskingum-Cunge method is an application of the concept of diffusion wave.
4.02
The method parallels the Muskingum method, but with the significant difference that the routing parameters are determined on a physical and numerical basis.
4.03
The physical characteristics are measurable hydraulic and cross-sectional properties; therefore, there is no need for streamgaging data, and the method can be used in ungaged streams.

4.04
In the Muskingum-Cunge method, the routing parameter K is:

      Δx
K =

       c

Eq. 18

4.05
The routing parameter X is:

      1          q_o
X =
(1 -
)
      2        S_ocΔx

Eq. 19

4.05
Defining the cell Reynolds number D:

        q_o
D =

      S_ocΔx

Eq. 20

4.06
The routing coefficients reduce to:

       -1 + C + D
C₀ =

        1 + C + D

Eq. 21

        1 + C - D
C₁ =

        1 + C + D

Eq. 22

        1 - C + D
C₂ =

        1 + C + D

Eq. 23

4.07
Thus, given space and time intervals, unit-width discharge, kinematic wave celerity, and bottom slope, the Courant and cell Reynolds numbers can be calculated.

4.08
Then, the routing coefficients of the Muskingum-Cunge method can be calculated, and the flood routing proceeds with the routing equation.

4.09
The Muskingum-Cunge method works by matching physical diffusion with numerical diffusion.

4.10
The method works best for Courant numbers close to 1, for which the numerical dispersion is minimized.

5. EXAMPLE

5.01
Assume an inflow hydrograph with peak flow 1000 m³/s, baseflow 0 m³/s, bottom slope = 0.000868, peak flow area = 400 m², peak flow top width = 100 m, rating exponent β = 1.6, reach length = 14,400 m, and time interval Δ t = 1 hour.

Q_p = 1000 m³/s
Q_b = 0 m³/s
S_o = 0.000868
A_p = 400 m²

Eq. 24

T_p = 100 m
β = 1.6
Δx = 14,400 m
Δt = 1 hour

Eq. 25

5.02
The mean velocity is:

V = Q_p/A_p = 1000/400 = 2.5 m/s

Eq. 26

5.03
The wave celerity is:

c = β V = 1.6 × 2.5 = 4 m/s

Eq. 27

5.04
The unit-width discharge is:

q = Q_p/T_p = 1000/100 = 10 m²/s

Eq. 28

5.05
The Courant number is:

C = c Δt/Δx
C = 4 × 3600 / 14400 = 1
Eq. 29

5.06
The cell Reynolds number is:

D = q/(S_o c Δx)
D = 10/(0.000868 × 4 × 14400) = 0.2

Eq. 30

5.07
The routing coefficients are:

C₀ = 0.091
C₁ = 0.818
C₂ = 0.091

Eq. 31

5.08

The routing computations are shown in this table.

Time Inflows C₀I₂ C₁I₁ C₂O₁ O

0 0 - - - 0

1 200 18.2 0.0 0.0 18.20

2 400 36.4 163.6 1.66 201.66

3 600 54.6 327.2 18.35 400.15

4 800 72.8 490.8 36.41 600.01

5 1000 91.0 654.4 54.60 800.00

6 800 72.8 818.0 72.80 963.60

7 600 54.6 654.4 87.69 796.69

8 400 36.4 490.8 72.50 599.70

9 200 18.2 327.2 54.57 399.97

10 0 0.0 163.6 36.4 200.00

11 0 0.0 0.0 18.2 18.2

12 0 0.0 0.0 1.66 1.66

13 0 0.0 0.0 0.16 0.16

5.09
Column 1 shows the time in hours.

5.10
Column 2 shows the inflow hydrograph.

5.11
Columns 3 to 5 show the weighted flows.

5.12
Column 6 shows the outflow hydrograph.

5.13
Note that the peak inflow is 1000 m³/s at time = 5 hr, while the peak outflow is 963.6 m³/s at time = 6 hr.

5.14
The flood peak has attenuated about 3%, and the time base has increased to 13 hr.

Fig. 01

Flood on the Chane river, Eastern Bolivia.

Fig. 02

Tinajones feeder canal, Lambayeque, Peru.

Fig. 03

Tinajones feeder canal, Lambayeque, Peru.

Fig. 04

Tinajones feeder canal, Lambayeque, Peru.

Fig. 05

Space and time discretization in the Muskingum scheme.

Narrator: Victor M. Ponce
Music: Fernando Oñate
Editor: Flor Pérez

Copyright © 2011
Visualab Productions
All rights reserved