|
OPEN-CHANNEL HYDRAULICS: LECTURE 104 - UNSTEADY RAPIDLY VARIED FLOW
1. SURFACE WAVES 1.01 Surface waves are unsteady open-channel flow features occurring at or around critical flow. Fig. 01
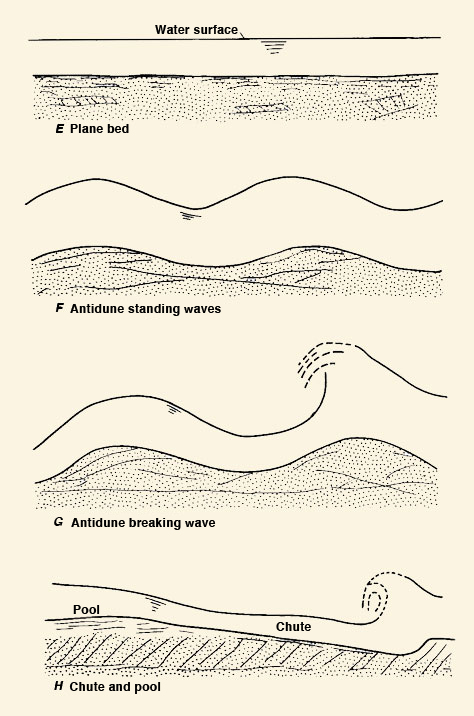
1.02 Surface waves are connected with the transition to upper regime, where surface perturbations are in phase with bed perturbations. Fig. 02
1.03 Surface waves are a manifestation of the instability of critical flow.
2. SURGES 2.01 Surges are perturbations created by sudden gate closures or rapid changes in stage or flow depth. 2.02 A surge does not attenuate readily, instead traveling along the channel for a considerable distance. 2.03 Surges are avoided by opening gates slowly, and minimizing the possibility of sudden stage or depth changes. 2.03 As a first approximation, the time of opening of a canal gate is:
Eq. 1
2.04 where uo is the mean velocity, So is the bottom slope, and g is the gravitational acceleration.
3. KINEMATIC SHOCKS 3.01 Kinematic shocks are kinematic waves that have steepened to the point where they become, for all practical purposes, a wall of water, with a nearly vertical upstream face. 3.02 Kinematic waves travel downstream, and can either steepen or flatten, depending on the interaction of the wave with the cross-sectional geometry. 3.03 Only kinematic waves that steepen can develop into kinematic shocks. 3.04 While kinematic waves are gradually varied, kinematic shocks are rapidy varied. 3.05 The development of a kinematic shock is a function of: 1. The type of wave. The more kinematic a wave is, the less it has the tendency to attenuate and, therefore, the more its tendency to steepen. 2. The baseflow. The smaller the base-to-peak flow ratio, the greater the tendency for the wave to steepen. This is due to wave nonlinearities, with inbank larger flows tending to travel with greater celerities. 3. The flow regime. High-Froude-number flows have less tendency to attenuate disturbances; therefore, the higher the Froude number, the lesser the attenuation. As the flow approaches the Vedernikov number equal to 1, the flow becomes neutrally stable and attenuation reduces to zero. 4. The type of cross section. Hydraulically wide channels with Manning friction, for which β = 5/3, have a greater tendency to steepen than triangular channels, for which β = 4/3. Inherently stable channels, for which β = 1, have no tendency to steepen. 3.06 Thus, kinematic shocks will develop in field situations involving a kinematic wave, an arid climate, a high flow rate, and a hydraulically wide channel. 3.07 This may be the case of an intense cloudburst rapidly concentrating through a canyon in a semiarid region. 3.08 A well-documented flash flood, which was in all probability a kinematic shock, occurred July 26, 1981, in Tanque Verde Creek, a tributary of the Santa Cruz river, in Eastern Arizona. 3.09 The flood, which killed 8 people, was, by all accounts, only a 2-yr flood. 3.10 However, the suddenness of the flood, which, according to survivors' reports, amounted to a wall of water, resulted in substantial loss of life. 3.11 Kinematic shocks have been observed with certain frequency in laboratory overland flow computations. 3.12 These computations are conducive to kinematic shock development. 3.13 This is due to the prescribed spatial regularity which is necessary to make the problem more tractable.
4. ROLL WAVES 4.01 Roll waves form in open-channel flow when the Vedernikov number exceeds 1. 4.02 Roll waves manifest themselves as a wave train moving downstream. Fig. 03
4.03 The Vedernikov number is the ratio of relative kinematic wave celerity to relative dynamic wave celerity.
Eq. 2
4.04 where v = mean velocity, and h = flow depth. 4.05 Roll waves occur when the relative kinematic wave celerity exceeds the relative dynamic wave celerity. 4.06 Since kinematic waves transport mass, and dynamic waves transport energy, roll waves occur at the threshold where mass and energy are being transported at the same speed. 4.07 In practice, roll waves occur in steep artificial channels, when the Vedernikov number exceeds 1. Fig. 04
4.08 The ratio between Vedernikov and Froude numbers is:
Eq. 3 4.09 The neutrally stable Froude number is that for which the Vedernikov number is equal to 1.
Eq. 4 4.10 Roll waves begin to form at the neutrally stable Froude number. Fig. 05
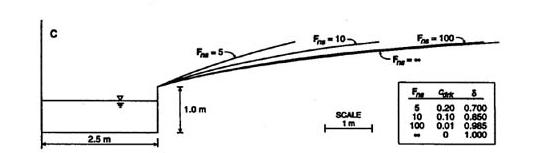
4.11 The neutrally stable Froude number is a function only of β. 4.12 In turn, β is a function of friction and cross-sectional shape. 4.13 This table shows neutrally stable Froude numbers for a wide range of friction and cross-sectional shapes.
4.14 This table shows that for the inherently stable channel, β is equal to 1; therefore, Q is equal to α A, and the velocity is a constant regardless of flow depth.
Eq. 5 4.15 For the inherently stable channel the neutrally stable Froude number is infinity. Therefore, the flow remains stable regardless of the Froude number. 4.16 An example of an inherently stable channel is shown here. Fig. 10
5. TIDAL BORES 5.01 Tidal bores form in certain estuaries in conjunction with large seasonal tidal ranges, usually on or around the equinoxes (March 21 and September 22). 5.02 Whether the tidal wave is able to move upstream into the estuary proper and develop into a recognizable bore of finite depth, depends on the tidal range and the cross-sectional geometry of the estuary. 5.03 Tidal bores are more likely to form in smooth hydraulically wide estuaries of relatively constant depth. Fig. 06
5.04 Large tidal bores have been observed in the Araguari river, in Amapa, Brazil, on the Severn river, in France, in the Quiantang river, in China, and in other selected estuaries around the world.
6. DEBRIS FLOWS 6.01 Debris flows are sudden accumulations of runoff containing great quantities of sediment particles, usually boulder size and above. 6.02 Debris flows travel downstream at great speeds, destroying everything along their path and threatening life and property. Fig. 07
6.03 Debris flows are induced by intense rains, but they can also be triggered by earthquakes. 6.04 In Southern California, along the base of the San Gabriel Mountains, east of Los Angeles, rain-induced debris flows recur with predictable regularity. 6.05 They are caused by: 1. Geologic uplift, making the San Gabriel Mountains the most tectonically active range in the United States. The uplift leads to slope steepening, which increases gravitational forces and maximizes erosion potential. 2. The prevailing chaparral ecosystem. The chaparral is endemic to the region, surviving the long droughts by developing singular adaptations which rely on wax protective surfaces for evapotranspiration suppression. 3. The wind. The region is home to the Santa Ana winds, which provide instant fire weather by featuring dry winds which can readily reach more than 40 mph. 4. Fire. Fire follows wind after a long drought, with the canopy not having burned for 30 years or more. 5. Rain. Rain follows fire due to ash particles in the air promoting coalescence and raindrop formation. 6.06 The sequence of wind, fire, and rain on a steep slope covered with chaparral is what triggers the debris flows in this region. 6.07 During fire, the waxlike substances vaporize at the surface and recondense at a certain depth inside the soil, producing the non-wettable layer. 6.08 The accumulation of intense rainfall, exceeding 25 mm per hour, below the surface and above the non-wettable layer, leads to the entrainment of large quantities of sediment which go on to constitute the debris flows. 6.09 A typical rain-induced debris flow in Southern California may carry away 10-50 mm of soil in a few hours. 6.10 By way of comparison, normal erosion rates are typically less than 1 mm per year. 6.11 Massive debris flows can be triggered by earthquakes. 6.12 Such was the case of the Huascaran slide on May 30, 1970, in Peru, which buried the town of Yungay and killed more than 20,000 people. 6.13 The town has since been rebuilt at a location just north of the ill-fated site.
7. LAHARS 7.01 Lahars are debris flows triggered by snowmelt as a result of a volcanic eruption and subsequent sudden melting of the snowcap. Fig. 08
7.02 The word 'lahar' originated in Indonesia, where the phenomenon is very common. 7.03 Lahars have the consistency, viscosity, and approximately the same density as concrete; fluid when moving, and solid when stopped. 7.04 Lahars can be massive and deadly, as shown by the November 13, 1985 eruption of the Nevado del Ruiz volcano, in Colombia. 7.05 Four lahars came down the river valleys on the volcano flanks. 7.06 The largest of them virtually destroyed the town of Armero, killing more than 75% of its 28,700 inhabitants. Fig. 09
Fig. 01
Fig. 02
Fig. 03
Fig. 04
Fig. 05
Fig. 06
Fig. 07
Fig. 08
Fig. 09
Fig. 10
Narrator: Victor M. Ponce Music: Fernando Oñate Editor: Flor Pérez
Copyright © 2011 Visualab Productions All rights reserved
|