OPEN-CHANNEL HYDRAULICS: LECTURE 113 - SEDIMENT TRANSPORT

1. SEDIMENT TRANSPORT MECHANICS
1.01
Sediment transport refers to the entrainment and movement of sediments by flowing water.
1.02
An understanding of the principles of sediment transport is essential for the interpretation and solution of many hydraulic engineering problems.
1.03
The study of sediment transport can be divided into:
1. Sediment transport mechanics,
2. Sediment transport prediction, and
3. Sediment routing.
1.04
Sediment transport mechanics refers to the processes by which sediments are entrained and transported by flowing water.
1.05
Sediment transport prediction refers to the methods to calculate the equilibrium or steady rate of sediment transport in streams and rivers.
1.06
The prediction of sediment transport is accomplished with a sediment transport formula.
1.07
Sediment routing refers to the nonequilibrium or unsteady sediment transport processes, the net result of which is either the aggradation or degradation of streams or river beds.
1.08
The energy and turbulence of the flow gives streams and rivers the capacity to entrain and transport sediment.
1.09
Entrainment and transport is a function of the vertical velocity gradient near the streambed.
1.10
The sediment being transported can originate in either upland or channel sources.
1.11
A significant feature of sediment transport is the entrainment and transport of the material constituting the streambed.
1.12
Thus, sediment transport is the mechanism by which streams and rivers determine their own cross sectional geometry and boundary roughness.
1.13
Sediment load or sediment discharge is the total amount of sediment transported by a stream or river past a given point, expressed in terms of weight per unit volume.
1.14
Based on the predominant mode of transport, sediment load can be classified into:
1. Bed load, and
2. Suspended load.
1.15
Bed load is the fraction of sediment load that moves by saltation and rolling along the streambed, primarily by action of bottom shear stresses caused by vertical velocity gradients.
1.16
Suspended load is the fraction of sediment load that moves in suspension by the action of turbulence.
1.17
Particles transported as bed load are coarser than particles transported as suspended load.
Fig. 02

Large boulders forming part of bedload, Rachichuela Creek, Lambayeque, Peru.

1.18
However, some particles may move as bed load at one point, and as suspended load at another.
1.19
Based on whether the particle sizes are represented in the streambed, sediment load can be classified into:
1. Bed material load, and
2. Fine material load.
1.20
Bed material load is the fraction of sediment load whose particle sizes are significantly represented in the streambed.
1.21
Fine material load, commonly referred to as "wash load," is the fraction of sediment load whose particle sizes are not significantly represented in the streambed.
1.22
Bed material load is the coarser fraction of sediment load, which may have originated in the channel bed, and that may be subject to deposition under certain conditions.
1.23
Wash load is the finer fraction of sediment load, that has not originated in the channel bed, and is not likely to deposit.
1.24
Wash load is largely unaffected by the hydraulics of the flow.
1.25
The relation between the two classifications of sediment load is shown in this table.

Relation between two classifications of sediment load Classification

Based on predominant mode of transport Based on whether particle sizes are represented in the channel bed

Total sediment load Wash load Suspended load Wash load

Suspended bed-material load Bed material load

Bed load Bed load

1.26
This table shows that bed load and wash load are mutually exclusive.
1.27
The middle overlap is the suspended bed material load, i.e., the fraction of sediment load that moves in suspended mode and is composed of particle sizes that are represented in the channel bed.

2. INITIATION OF MOTION
2.01
Water flowing over a streambed has a marked vertical velocity gradient near the streambed.
2.02
This velocity gradient exerts a shear stress on the particles lying on the streambed, that is, a bottom shear stress.
2.03
For hydraulically wide channels, the bottom shear stress is:

τ_o = γ d S_o

Eq. 1

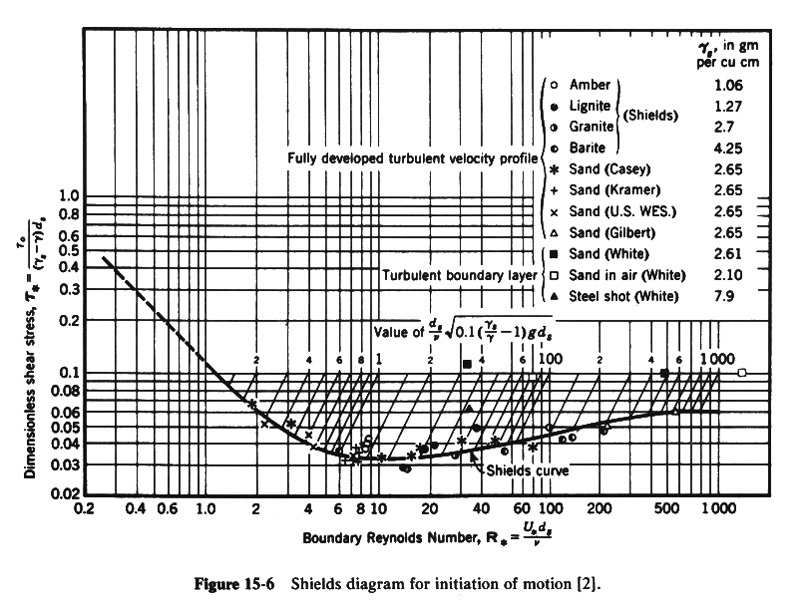
2.04
in which
τ_o = bottom shear stress
γ = specific weight of water
d = flow depth, and
S_o = equilibrium or energy slope.
2.05
There is a threshold value of bottom shear stress above which the particles actually begin to move.
2.06
This threshold value is referred to as the critical bottom shear stress, or critical tractive stress.
2.07
The Shields diagram shown here, developed in 1936, is the earliest attempt to combine theoretical and empirical approaches to estimate critical tractive stress.
Fig. 03

Shields diagram for initiation of motion.

2.08
This diagram depicts the threshold of motion, that is, the condition separating motion, above the curve, from no motion, below the curve.
2.09
The abscissa in the Shields diagram is the boundary Reynolds number, defined as:

       U_* d_s
R_* =

         ν

Eq. 2

2.10
in which
U_* is the shear velocity,
d_s is the mean particle diameter, and
ν is the kinematic viscosity of water.
2.11
The shear velocity is defined as:

        τ_o
U_* = (
)^1/2
        ρ

Eq. 3

2.12
in which ρ is the density of water.
2.13
The ordinate in the Shields diagram is the dimensionless tractive stress, defined as:

           τ_o
τ_* =

       (γ_s - γ) d_s

Eq. 4

2.14
in which τ_* is the dimensionless tractive stress, and γ_s is the specific weight of the sediment particles.
2.15
The Shields diagram shows that, within a midrange of boundary Reynolds numbers, say from 2 to 200, the dimensionless critical tractive stress can be taken as a constant for practical purposes.
2.16
Within this range, the critical tractive stress is proportional to the sediment size.
2.17
For instance, assuming a dimensionless critical tractive stress equal to 0.04 from the Shields diagram, the critical tractive stress is:

τ_c = 0.04 (γ_s - γ) d_s

Eq. 5

2.18
For quartz particles, the specific weight of the sediment particles is:

γ_s = 2.65 (62.4) = 165.36 lbs/ft³

Eq. 6

2.19
The critical tractive stress reduces to:

τ_c = 0.04 (1.65) (62.4) d_s = 4.12 d_s

Eq. 7

2.20
In this equation, the critical tractive stress is in lbs per square foot, and the particle diameter in feet. With particle diameter in inches:

τ_c = 0.34 d₅₀

Eq. 7

2.21
in which d₅₀ is the mean particle diameter.
2.22
This equation compares favorably with Lane's equation for permissible tractive stress:

τ_c = 0.4 d₇₅

Eq. 8

2.23
in which d₇₅ is the particle diameter for which 75 percent of the material, by weight, is finer.
2.24
The initiation of motion by Shields' criterion can be calculated online at: http://onlinecalc.sdsu.edu/onlineshields.php

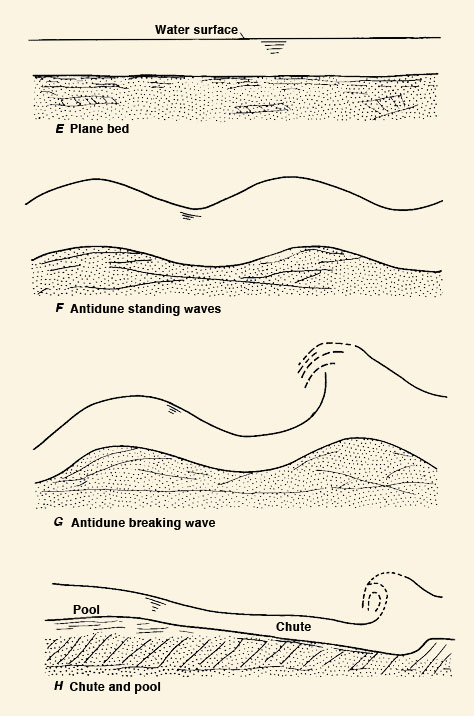
3. FORMS OF BED ROUGHNESS
3.01
Streams and rivers create their own geometry.
3.02
Alluvial rivers determine their cross-sectional shape and boundary friction as a function of the prevailing water and sediment discharge.
3.03
An inherent property of river flows is their tendency to minimize changes in stage caused by changes in discharge.
3.04
This is accomplished through a continuous adjustment in boundary friction in such a way that high values of friction prevail during low flows and low values prevail during high flows.
3.05
Adjustments in boundary friction are made possible by the existence of bedforms, which develop during low flows and are obliterated during high flows.
3.06
Boundary friction consists of two parts:
1. Grain roughness, and
2. Form roughness.
3.07
Grain roughness is a function of particle size.
3.08
Form roughness is a function of the size and extent of bedforms.
3.09
Grain roughness is essentially a constant, while form roughness varies with the flow.
3.10
Several forms of bed roughness can exist in rivers.
3.11
In the absence of sediment movement, the bed configuration is that of plane bed with no sediment motion.
3.12
With sediment movement, the following forms of bed roughness have been identified:
1. ripples,
2. dunes and superposed ripples,
3. dunes,
4. washed-out dunes,
5. plane bed,
6. antidunes standing waves, and
7. antidunes breaking wave, and
8. chute and pool.
3.13
Sketches of these forms of bed roughness are shown here.
Fig. 06

Forms of bed roughness.

Fig. 07

Forms of bed roughness.

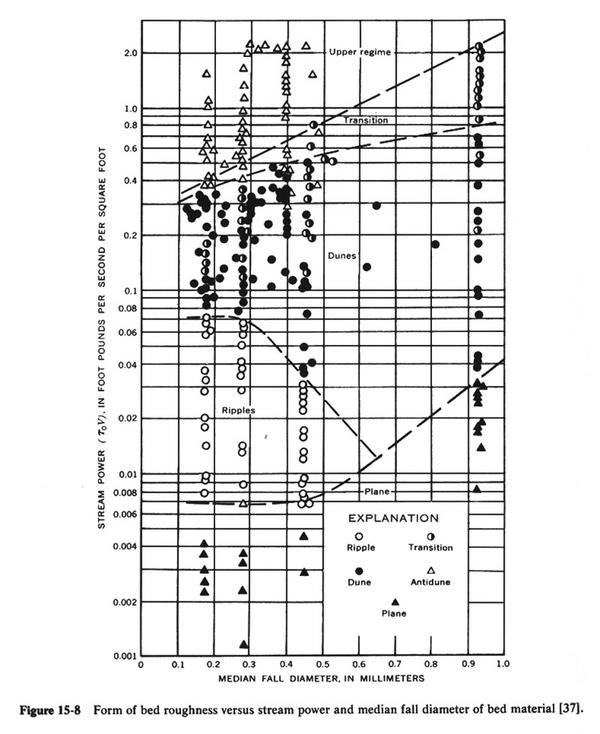
3.14
The occurrence of different forms of bed roughness is related to the median fall diameter of the bed material and the stream power of the flow.
3.15
Stream power is defined as the product of bottom shear stress and mean velocity.

SP = τ_o v

Eq. 9

3.16
The stream power-median fall diameter diagram is shown here.
Fig. 04

Relation between stream power and mean fall diameter.

3.17
For low stream power, there is no bedload transport. This is the condition of plane bed with no sediment motion.
3.18
An increase in stream power leads to ripples, then to dunes with superposed ripples, and subsequently, to dunes.
3.19
However, ripples are a rare occurrence for sediments coarser than 0.6 mm.
3.20
Dunes are longer and bigger than ripples, and occur at velocities and sediment loads that are greater than those of ripples.
3.21
Plane bed with sediment motion occurs when the stream power is large enough to obliterate the dunes, essentially eliminating form roughness.
3.22
The plane bed represents the condition of minimum boundary friction.
3.23
For high values of stream power, antidunes form in conjunction with surface waves, usually under supercritical flow conditions.
3.24
In very steep streams, the bed configuration resembles a series of chutes and pools.
3.25
The assessment of bedform type has significant practical implications.
3.26
Bedforms determine boundary roughness; in turn, boundary roughness determines river stages.
3.27
Ripples are associated with Manning's n in the range 0.018-0.030, with form roughness usually being a fraction of grain roughness.
3.28
Dunes are associated with Manning's n in the range 0.020-0.040, with form roughness of the same order of magnitude as grain roughness.
3.29
Plane bed with sediment motion is associated with relatively low Manning's n values, in the range 0.012-0.015, with minimal form roughness.

4. SEDIMENT CONCENTRATION
4.01
For a given volume of water-sediment mixture, the suspended sediment concentration is the ratio of the weight of dry sediment to the weight of the water-sediment mixture, expressed in parts per million.
4.02
To convert the concentration in parts per million to milligrams per liter, multiply the value in parts per million times a factor f. This factor varies from 1 for concentrations less than 15,900 ppm, to 1.3 for concentrations of 380,000, as shown here.

C_s (ppm) f

≤ 15900 1

46900 1.02

76900 1.04

105000 1.06

132000 1.08

159000 1.1

279000 1.2

380000 1.3

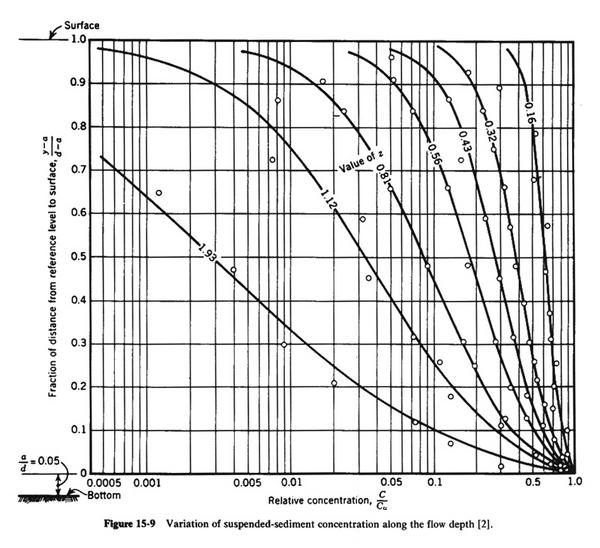
4.03
For low sediment concentrations, typical of most applications, concentrations in parts per million and milligrams per liter are essentially equivalent.
4.04
The suspended sediment concentration varies along the vertical.
4.05
It is higher near the streambed and lower near the water surface.
4.06
The coarsest sediment fractions, typically those in the sand size, exhibit the greatest variation in concentration along the vertical.
4.07
Conversely, the finer fractions, that is, those of silt and clay size, show a tendency for a nearly uniform distribution of concentration along the vertical.
4.08
The trend is depicted in the dimensionless chart shown here.
Fig. 05

Variation of suspended-sediment concentration along the flow depth.

4.09
In this chart, the abscissa is the relative sediment concentration, defined as the sediment concentration along the flow depth, divided by the concentration at a reference distance equal to 5 percent of the flow depth.
4.10
The ordinate is the relative distance, or the distance measured along the depth, divided by the flow depth. In either case, 5 percent of the flow depth is substracted from the actual values.
4.11
The curve parameter is the Rouse number:

        w
z =

      β κ U_*

Eq. 10

4.12
in which
w is the fall velocity of sediment particles,
β is a coefficient relating mass and momentum transfer, equal to 1 for fine sediments,
κ is von Karman's constant, equal to 0.4 for clear fluids, and
U_* is the shear velocity.
4.13
The figure shows that high Rouse numbers, on the order of 1.93, correspond to the sand sizes, while low Rouse numbers, around 0.16, correspond to the clay sizes.

5. SEDIMENT TRANSPORT FORMULAS
5.01
The terms sediment load, sediment discharge, and sediment transport rate are synonymous.
5.02
However, the terms bed load, suspended bed material load, and wash load are mutually exclusive.
Fig. 12

Mantaro river, Junin, Peru.

5.03
Sediment transport prediction refers to the estimation of sediment transport rates under steady equilibrium flow conditions.
5.04
There are many formulas for the calculation of sediment transport.
5.05
Most formulas compute only bed material load, consisting of bed load and suspended bed material load.
5.06
Some formulas compute bed load only.
5.07
One formula computes total sediment load, which consists of bed load, suspended bed material load, and wash load.
5.08
All sediment transport formulas have empirical components; therefore, they are most applicable within the range of data used in their development.
5.09
The Duboys formula is widely recognized as one of the earliest attempts to develop a sediment transport predictor.
5.10
The Duboys formula is:

q_s = ψ_D τ_o (τ_o - τ_c)

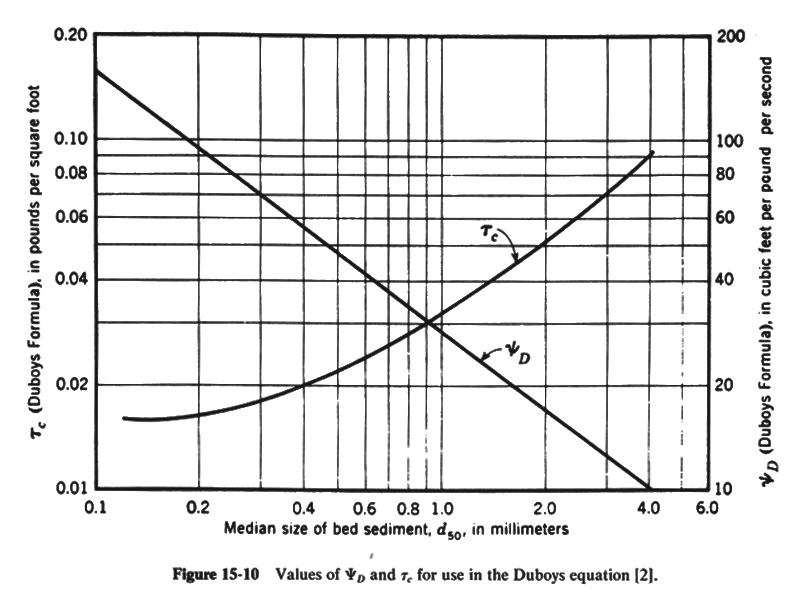
Eq. 11

5.11
in which
q_s is the unit-width bed material transport rate, in lbs per second per foot,
ψ_D is the Duboys parameter, which varies with the particle size, and has units of cubic feet per pound per second,
τ_o is the bottom shear stress, in lbs per square foot, and
τ_c is the critical tractive stress, in lbs per square foot.
5.12
Values of the Duboys parameter and critical shear stress as a function of particle size are shown here.
Fig. 08

Values of ψ_D and τ_c for use in the Duboys equation.

5.13
The Duboys formula can be calculated online at this address:
http://onlinecalc.sdsu.edu/onlineduboys.php
5.14
In 1950, Professor Hans Einstein published a procedure for the computation of sediment load by size fractions.
5.15
The method is referred to as Einstein's bedload function.
5.16
It was developed based on theoretical considerations of turbulent flow, supported by laboratory and field data.
5.17
Einstein's bed load function first computes the bed load transport rate.
5.18
Then it uses this transport rate to aid in the integration of the suspended sediment concentration profile and the flow velocity profile.
5.19
The result is the the bed-material transport rate, per individual size fractions.
5.20
The Einstein bedload function is the basis of the Modified Einstein Procedure.
5.21
This procedure was developed by Colby and Hembree in 1955 in order to include actual measurements of suspended load into the framework of the original Einstein method.
Fig. 13

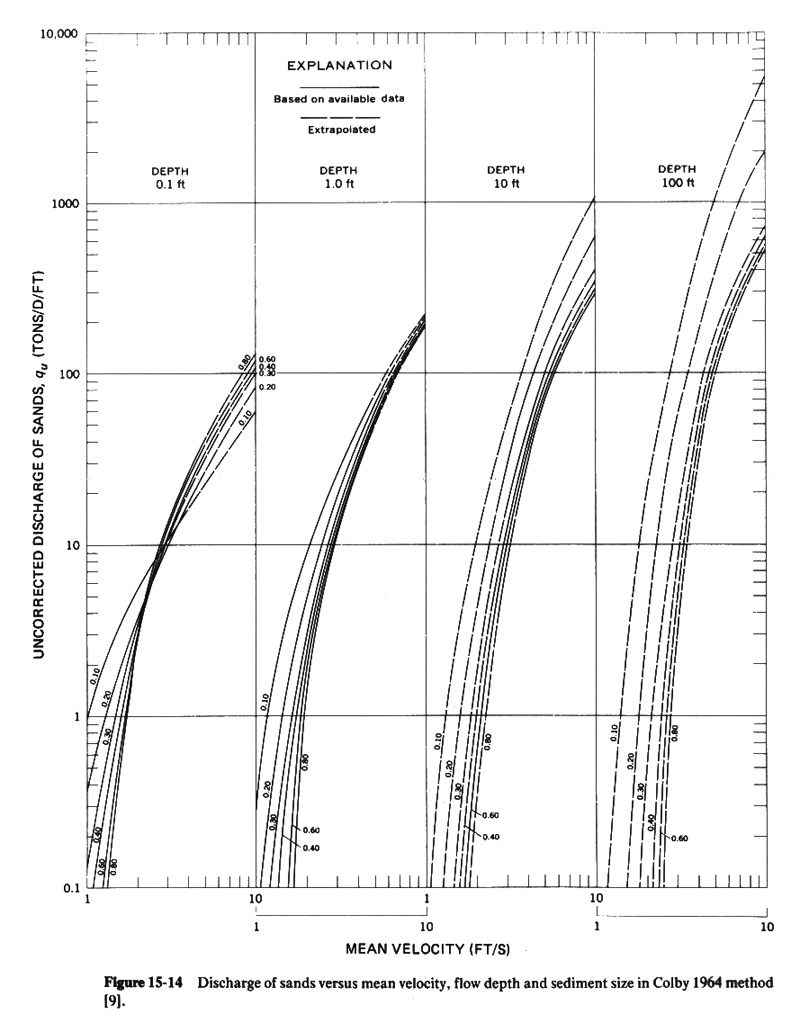
Tinajones feeder canal, Lambayeque, Peru.

5.22
Typically, measurements of suspended load do not include (a) the bed load and (b) the fraction of suspended load moving too close to the streambed to be effectively sampled.
5.23
The Modified Einstein Procedure calculates total sediment load, by size fractions, consisting of bed load, suspended bed material load, and wash load.
5.24
It requires the measured fraction as input, and calculates the unmeasured fraction. Thus, it is the most complete method for sediment transport computations.
5.25
The Modified Einstein Procedure can be calculated online at this address:
http://onlinecalc.sdsu.edu/onlinemodifiedeinstein.php
5.26
In 1964, Colby published a method to calculate the discharge of sands in sandbed streams.
5.27
The development of the Colby method was guided by the Einstein bed load function and supported by large amounts of laboratory and field data.
5.28
The method provides a good prediction of bed-material transport rate in the sand sizes.
5.29
It requires the following input data:
1. Mean flow depth,
2. Mean channel width,
3. Mean velocity,
4. Water temperature,
5. Wash-load concentration, and
6. Median bed-material size.
5.30
The procedure is as follows:
1. Use this figure to determine the uncorrected discharge of sands q_u, as a function of depth, mean velocity, and sediment size.
Fig. 09

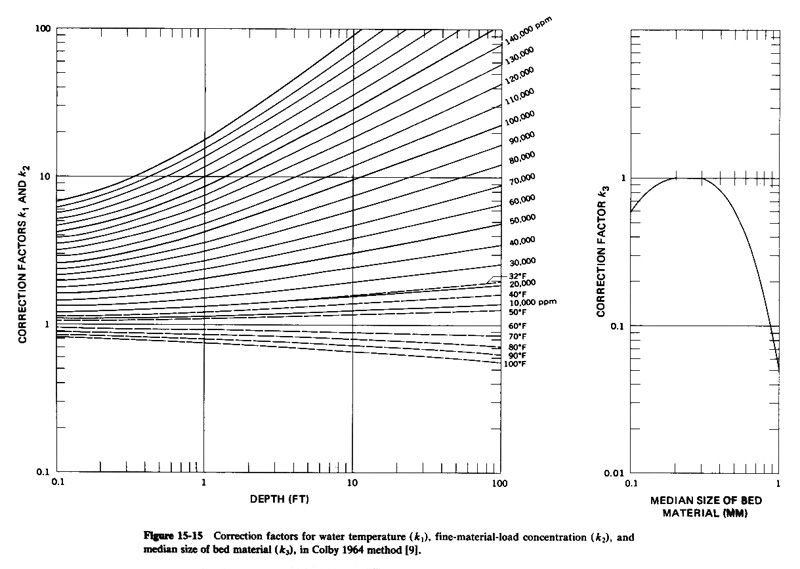
Discharge of sands by the Colby method.

2. For water temperature of 60 degrees Farenheit, wash-load concentration less than 1000 ppm, and sediment size in the range 0.2-0.3 mm, no further correction is required.
3. For other conditions, use this figure to determine the correction factor k₁ for temperature, k₂ for wash-load concentration, and k₃ for bed-material size.
Fig. 10

Correction factors in the Colby method.

5.31
The corrected discharge of sands q_s is:

q_s = [1 + (k₁k₂ - 1)k₃] q_u

Eq. 11

5.32
The Colby method can be calculated online at this address:
http://onlinecalc.sdsu.edu/onlinecolby.php

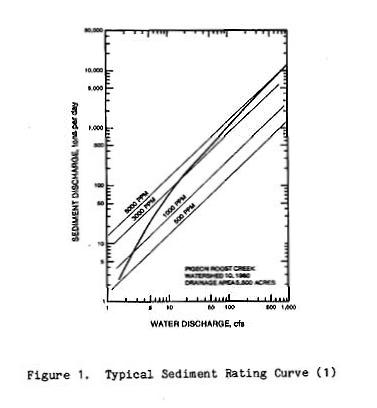
6. SEDIMENT RATING CURVES
6.01
A useful curve in sediment analysis is the sediment rating curve, defined as the relation between water discharge and sediment discharge at a given site.
6.02
For a given water discharge, the sediment rating curve allows the estimation of sediment discharge, assuming steady equilibrium flow conditions.
6.03
The sediment rating curve is a plot showing water discharge in the abscissas and sediment discharge in the ordinates.
6.04
This plot is obtained either (a) by the simultaneous measurement of water and sediment discharge or (b) by the use of sediment transport formulas.
6.05
For low water discharges, the sediment rating curve usually shows an increase in sediment concentration with water discharge.
6.06
For high water discharges, the sediment rating curve has a tendency to approach asymptotically a line of equal sediment concentration, as shown here.
Fig. 11

Typical sediment rating curve.

6.07
This difference in behavior is attributed to the varying effect of form friction on sediment transport from low to high flow rates.
6.08
Like the single-valued stage-discharge rating, the single-valued sediment rating curve is strictly valid only for steady equilibrium flow conditions.
6.09
For strongly unsteady flows, the existence of loops in both water and sediment rating curves has been demonstrated.
6.10
These loops are complex in nature and are likely to vary from flood to flood.
6.11
In practice, loops in both water and sediment rating are commonly disregarded.

7. SEDIMENT ROUTING
7.01
The calculation of sediment yield is of zero order, that is, it does not provide a measure of the spatial or temporal variability of sediment production or yield within the watershed or basin.
7.02
Sediment transport formulas are invariably based on the assumption of steady uniform flow.
7.03
Sediment routing refers to the distributed and unsteady calculation of sediment production, transport, and deposition in catchments, streams, rivers, reservoirs, and estuaries.
7.04
Sediment routing is used where the description of spatial and temporal variations of sediment production, transport, and deposition is warranted.
7.05
The sediment continuity equation, also referred to as the Exner equation, is used in sediment routing.
7.06
The equation states the balance between the gradient of sediment transport rate and the rate of change in bed elevation within a control volume.

  ∂q_s               ∂z

+ (1 - p) γ_s
= 0
  ∂x                ∂t

Eq. 12

7.07
in which g_s is the unit-width bed-material transport rate, z is the bed elevation, p is the porosity of the material forming the streambed, and γ_s is the specific weight of the sediment particles.
7.08
Sediment routing is particularly useful in studies of aggradation and degradation in rivers and reservoirs.

Fig. 02

Large boulders forming part of bedload, Rachichuela Creek, Lambayeque, Peru.

Fig. 03

Shields diagram for initiation of motion.

Fig. 04

Relation between stream power and mean fall diameter.

Fig. 05

Variation of suspended-sediment concentration along the flow depth.

Fig. 06

Forms of bed roughness.

Fig. 07

Forms of bed roughness.

Fig. 08

Values of ψ_D and τ_c for use in the Duboys equation.

Fig. 09

Discharge of sands by the Colby method.

Fig. 10

Correction factors in the Colby method.

Fig. 11

Typical sediment rating curve.

Fig. 12

Mantaro river, Junin, Peru.

Fig. 13

Tinajones feeder canal, Lambayeque, Peru.

Narrator: Victor M. Ponce
Music: Fernando Oñate
Editor: Flor Pérez

Copyright © 2011
Visualab Productions
All rights reserved