QUESTIONS
Name three properties that characterize a small catchment. Explain each one of them.
|
The following characteristics describe a small catchment: (1) rainfall
can be assumed to be uniformly distributed in time, (2) rainfall can be
assumed to be uniformly distributed in space, (3) storm duration usually
exceeds concentration time, (4) runoff is primarily by overland flow, and
(5) channel storage processes are negligible.
For a small catchment, storm duration is so short that rainfall can be assumed to be uniformly
distributed in time.
Also, for a small catchment, it is usually sufficient to assume uniform rainfall distribution in space.
For a small catchment, the concentration time is so short that an assumption of concentrated catchment flow (i.e., storm duration greater than concentration time) is generally justified.
|
What hydrologic processes does the rational method account for? Explain how they affect runoff.
|
The rational method takes into account the following hydrologic
characteristics or processes: (1) rainfall intensity, (2) rainfall
duration, (3) rainfall frequency, (4) catchment area, (5) hydrologic
abstractions, (6) runoff concentration, and (7) runoff diffusion.
Rainfall intensity is directly related to runoff. Rainfall duration
determines the time of concentration, and, therefore, rainfall intensity
and runoff. Rainfall frequency determines rainfall intensity and runoff.
Catchment area determines the potential amount of runoff. Hydrologic
abstractions determine the effective precipitation, and, therefore, the
runoff amounts. Runoff concentration has a bearing on the amount of peak
runoff developed from a catchment. Runoff diffusion has the effect of
attenuating the runoff hydrograph, with the consequent reduction of flood
peaks.
|
What processes are not considered in the rational method? Explain.
|
The rational method does not take into account the following
characteristics or processes: (1) spatial or temporal variations in
either total or effective rainfall; (2) concentration time much greater
than the rainfall duration; (3) a significant portion of the runoff
occurring in the form of streamflow. In addition, the rational method
does not directly account for the catchment's antecedent moisture
condition, although the latter may be implicitly accounted for by varying
the runoff coefficient.
|
How are the frequencies of storms and floods related? How does the rational method account for this difference?
|
In nature, the frequencies of storms and floods are not necessarily the
same, largely due to the effect of antecedent moisture condition,
variability in channel transmission losses, overbank storage, and the
like. In the rational method, the runoff coefficients are usually
adjusted upward to reflect postulated decreases in runoff frequency
(increases in return period).
|
What processes are included in the runoff coefficient?
|
The processes included in the runoff coefficient are primarily hydrologic
abstractions and runoff diffusion, and secondarily, flood frequency.
Hydrologic abstractions include interception, infiltration, surface
storage, evaporation, and evapotranspiration. Runoff diffusion is a
measure of the catchment's ability to attenuate the flood peaks.
Postulated decreases in flood frequency can be simulated with an upward
adjustment of the runoff coefficient.
|
Under what assumption does the rational method provide the shape of the outflow hydrograph?
|
The rational method provides the shape of the outflow hydrograph under
the assumption of runoff concentration without diffusion. In this case
the outflow hydrograph is an isosceles triangle, with recession time
equal to rising time.
|
Describe the phenomenon of overland flow. Contrast overland flow analysis with the rational method approach.
|
Overland flow is surface runoff that occurs in the form of sheet flow on
the land surface without concentrating in clearly defined channels. This
type of flow is the first manifestation of surface runoff, since the
latter occurs first as overland flow before it has the chance to flow
into channels and become streamflow.
Overland flow analysis is generally a deterministic method, whereas the
rational method is parametric. Overland flow calculations tend to be
very complex, while the rational method is relatively simple to use.
Overland flow produces a runoff hydrograph; the rational method produces
a runoff hydrograph (an isosceles triangle) only under the assumption of
runoff concentration without diffusion.
|
What crucial assumption makes the storage solution of overland flow different from the kinematic wave solution?
|
The storage solution of overland flow is based on a single-valued rating
between outflow and storage, at equilibrium and at any other time. Since
storage refers to the total volume of water stored on the overland flow
plane, this assumption effectively renders the storage solution a lumped
model. On the other hand, the kinematic wave solution is based on a
single-valued rating between discharge and flow depth, at any point in
space and time, rendering it a distributed model.
|
Why is overland flow likely to be of mixed laminar-turbulent nature? How is this modeled in practice?
|
Overland flow is likely to be of mixed laminar-turbulent nature because
of the relatively small flow depths and the large variation of flow
depths within the overland flow plane. In practice, the Manning equation
is used to model the mixed laminar-turbulent flow regime, with the
Manning friction coefficient adjusted upward to account for the mixed
laminar-turbulent nature of the flow regime.
|
What is the difference between the time of concentation (or time to equilibrium) in
storage-concept and kinematic-wave overland flow models?
|
The time-to-equilibrium of a kinematic-wave overland flow model (Eq. 4-54) is equal to one-half of that of the storage concept (Eq. 4-29).
|
What is an ideal reservoir? An ideal channel? Contrast these two concepts.
|
An ideal reservoir is a free-surface flow feature in which the water
surface slope is zero and, therefore, outflow and storage volume are
uniquely related. An ideal channel is a free-surface flow feature in
which the water surface slope is nonzero, and, consequently, storage is
generally a nonunique function of inflow and outflow. Ideal reservoirs
and ideal channels are quite different in nature and are, therefore,
handled differently in hydrologic computations. Reservoirs lend
themselves readily to lumped computation, whereas channels are more
suited to distributed computation.
|
What is the kinematic wave celerity? Why is it generally greater than the flow velocity?
|
The kinematic wave celerity is the velocity of a kinematic wave, defined
as c = mu,
in which
c = celerity of kinematic wave; m = exponent of the
flow-depth rating (q = bh m); and
u = mean flow velocity.
Since m is generally greater than 1, the celerity of a kinematic wave is generally greater than the mean flow velocity.
|
What is the kinematic flow number? What does it describe? For what kind of channel slope is it likely that the kinematic wave solution would not be applicable?
|
The kinematic flow number is a dimensionless number which measures the
kinematicity of the flow, i.e. whether the unsteady flow can be construed
as kinematic flow and therefore subject to kinematic wave modeling. The
kinematic flow number is defined as follows:
SoL
K = _______________
Fo2ho
|
in which K = kinematic flow number; So = plane or bed slope; L = plane
length; F = Froude number corresponding to the equilibrium flow at the
outlet; and h = equilibrium flow depth at the outlet.
Values of K greater than 90 describe kinematic flow, whereas lower values do not.
The kinematic wave solution is not applicable to mild bed slopes, because
the milder the bed slope, the lower the K value. Other variables in the
definition of K do not vary as widely as bed slope.
|
What is kinematic shock? Why does it often occur in analytic kinematic wave solutions while it is seldom present in numerical solutions?
|
Kinematic shock is the result of the steepening of the nonlinear
kinematic wave to the point where it attains an almost vertical face.
The kinematic shock prevails in analytic nonlinear kinematic wave
solutions because of the total absence of runoff diffusion. In actual
applications, a small but perceptible amount of runoff diffusion tends to
counteract the development of the kinematic shock. In numerical
solutions, numerical diffusion acts in such a way as to counteract the
development of kinematic shock, with the result that numerical solutions
seldom develop kinematic shock.
|
Contrast kinematic and diffusion wave approaches to overland flow.
|
Kinematic waves do not calculate runoff diffusion directly; they do so
indirectly by the introduction of numerical diffusion. Diffusion waves
can calculate runoff diffusion. Kinematic waves are limited to steep
channels and slow-rising hydrographs.
Diffusion waves are applicable to a wider range of problems than kinematic waves. Kinematic waves are
generally applicable to overland flow computations. Diffusion waves are
more appropriate for stream channel routing.
|
Why does Eq. 4-59 describe runoff diffusion, while Eq. 4-43 does not?
|
Equation 4-59 describes runoff diffusion because it contains a
second-order term which accounts for the diffusion process. On the other
hand, Eq. 4-43 does not contain a second-order term; therefore, it cannot
describe runoff diffusion.
|
What is hydraulic diffusivity?
|
Hydraulic or channel diffusivity is the
diffusion coefficient of the diffusion wave equation, Eq. 4-59.
|
PROBLEMS
Rain falls on a 150-ha catchment with intensity 2 cm/h and duration 2 h. Use the rational method to calculate the peak runoff, assuming runoff coefficient C = 0.6 and time of concentration tc = 1.5 h.
|
Since rainfall duration is greater than time of concentration, the flow
is superconcentrated.
Therefore, the peak runoff is: Qp = CIA =
(0.6 × 2 cm/h × 150 ha × 10,000 m2/ha × 0.01 m/cm) / (3600 s/h) =
Qp = 5 m3/s. ANSWER.
|
Rain falls on a 300-ac watershed with intensity 0.5 in./h and duration 2 h. Use the rational method to calculate the peak runoff, assuming runoff coefficient C = 0.4 and time of concentration tc = 2 h.
|
Since rainfall duration is equal to time of concentration, the flow is
concentrated.
Therefore, the peak runoff is: Qp = CIA =
(0.4 × 0.5 in./h × 300 ac × 43,560 ft2/ac) / (12 in./ft × 3600 s/h) =
Qp = 60.5 ft3/s. ANSWER.
|
Rain falls on a 545-ha catchment with intensity 45 mm/h and duration 1 h. Use the rational method to calculate the peak runoff for the following conditions:
- Natural, with time of concentration 2 h and C = 0.4;
- Improved, partially paved area, with time of concentration tc = 1 h and C = 0.7.
State any assumptions used.
|
(a) Since rainfall duration is 1 h and time of concentration is 2 h,
the flow is subconcentrated. Assume that 1/2 of the catchment is
contributing to the peak runoff at the time of cessation of rainfall.
Therefore, the peak runoff is:
Qp = CI(A/2) = (0.4 × 45 mm/h × 272.5 ha × 10,000 m2/ha × 0.001 m/mm) / (3600 s/h)
Qp = 13.6 m3/s. ANSWER.
(b) Since time of concentration is equal to rainfall duration, the flow
is concentrated and the entire catchment is contributing. Therefore,
the peak runoff is:
Qp = CIA = (0.7 × 45 mm/h × 545 ha × 10,000 m2/ha × 0.001 m/mm) / (3600 s/h)
Qp = 47.7 m3/s. ANSWER.
|
Rain falls on a 1.5-km2 watershed with intensity 20 mm/h and duration 2 h. Use the rational method to calculate the peak runoff for the following two conditions:
- Vegetated (natural) watershed with time of concentration tc = 3 h and C = 0.3; and
- Improved, partially paved area with time of concentration tc = 2 h and C = 0.6.
State any assumptions used.
|
(a) Since rainfall duration is 2 h and time of concentration is 3 h,
the flow is subconcentrated. Assume that 2/3 of the catchment is
contributing to the peak runoff at the time of cessation of rainfall.
Therefore, the peak runoff is:
Qp = CI [(2/3)A] = (0.3 × 20 mm/h × 1 km2 × 1,000,000 m2/km2 × 0.001 m/mm) / (3600 s/h)
Qp = 1.67 m3/s. ANSWER.
(b) Since time of concentration is equal to rainfall duration, the flow
is concentrated and the entire catchment is contributing.
Therefore,
the peak runoff is:
Qp = CIA = (0.6 × 20 mm/h × 1.5 km2 × 1,000,000 m2/km2 × 0.001 m/mm) / (3600 s/h)
Qp = 5 m3/s. ANSWER.
|
Rain falls on a catchment with intensity 35 mm/h and duration 2 h. The catchment area is 250 ha, with time of concentration tc = 2 hand φ = 15 mm/h. Calculate the peak runoff. State any assumptions used.
|
Assuming (1) absence of runoff diffusion, and (2) constant total and
effective rainfall intensities, the runoff coefficient is calculated by
Eq. 4-13:
C = (I - φ)/I = (35 mm/h - 15 mm/h) / (35 mm/h) = 0.57.
Since time of concentration is equal to rainfall duration, the flow is
concentrated and the entire catchment is contributing.
Therefore, the peak runoff is:
Qp = CIA = (0.57 × 35 mm/h × 250 ha × 10,000 m2/ha × 0.001 /mm) / (3600 s/h)
Qp = 13.9 m3/s. ANSWER.
|
Rain falls on a watershed with intensity 1 in./h and duration 3 h. The watershed area is 500 ac, with time of concentration tc = 2 h and φ = 0.3 in./h. Calculate the peak runoff. State any assumptions used.
|
Assuming (1) absence of runoff diffusion, and (2) constant total and
effective rainfall intensities, the runoff coefficient is calculated by
Eq. 4-13:
C = (I - φ)/I = (1 in/h - 0.3 in/h) / (1 in/h) = 0.7.
Since rainfall duration is greater than time of concentration, the
flow is superconcentrated and the entire watershed is contributing. Therefore, the peak runoff is:
Qp = CIA = (0.7 × 1 in/h × 500 ac × 43,560 ft2/ac) / (12 in/ft × 3600 s/h)
Qp = 353 ft3/s. ANSWER.
|
Rain falls on a watershed with intensity 30 mm/h and duration 1 h. The watershed area is 0.8 km2 with time of concentration tc = 2 h and φ = 15 mm/h. Use the rational method to calculate the peak runoff. State any assumptions used.
|
Assuming (1) absence of runoff diffusion, and (2) constant total and
effective rainfall intensities, the runoff coefficient is calculated by
Eq. 4-13:
C = (I - φ)/I = (30 mm/h - 15 mm/h)/(30 mm/h) = 0.5.
Since rainfall duration is 1/2 of the time of concentration, the flow
is subconcentrated. Assume that 1/2 of the watershed is contributing
to runoff at the time of cessation of rainfall. Therefore, the peak runoff is:
Qp = CI (A/2) = (0.5 × 30 mm/h × 0.4 km2 × 1,000,000 m2/km2 × 0.001 m/mm) /(3600 s/h)
Qp = 1.67 m3/s. ANSWER.
|
Rain falls on a 125-ha catchment with the following characteristics:
- 20%, C = 0.3;
- 30%, C = 0.4;
- 50%, C = 0.6.
Calculate the peak runoff due to a storm of 45 mm/h intensity lasting 1 h. Assume time of concentration tc = 30 min.
|
Since rainfall duration is greater than time of concentration, the flow
is superconcentrated and the entire catchment is contributing. For
subcatchments with different runoff coefficients, use a weighted
formula for peak runoff (see Eq. 4-14):
Qp = I Σ(CA)
Qp = 45 mm/h × [(0.3 × 125 × 20/100) + (0.4 × 125 × 30/100) + (0.6 × 125 × 50/100)] ha ×
(10,000 m2/ha × 0.001 m/mm) / (3600 s/h)
Qp = 7.5 m3/s. ANSWER.
|
Rain falls on a 90-ha catchment with the following characteristics:
- 12 ha, C = 0.3;
- 48 ha, C = 0.7;
- 30 ha, C = 0.9.
Calculate the peak runoff from a 50 mm/h storm lasting 2 h. Assume time of concentration tc = 2 h.
|
Since time of concentration is equal to rainfall duration, the flow is
concentrated and the entire catchment is contributing. For
subcatchments with different runoff coefficients, use a weighted
formula for peak runoff (see Eq. 4-14):
Q = I Σ(CA)
Qp = 50 mm/h × [(0.3 × 12) + (0.7 × 48) + (0.9 × 30)] ha × (10,000 m2/ha X 0.001 m/mm) / (3600 s/h)
Qp = 8.92 m3/s. ANSWER.
|
Rain falls on a 300-ha composite catchment which drains two subareas, as follows:
- Subarea A, steep, draining 20%, with time of concentration 10 min and C = 0.8; and
- Subarea B, milder steep, draining 80%, with time of concentration 60 min and C= 0.4.
Calculate the peak runoff corresponding to the 25-y-frequency. Use the following IDF function:
800T 0.2
I = ______________
(tr + 15) 0.7
| |
in which I = rainfall intensity in millimeters per hour, T = return period in years, and tr = rainfall duration in minutes. Assume linear flow concentration at the catchment outlet.
|
Several rainfall durations are tried, as shown in the following table
tr
(min) |
I
(mm/h) |
Subarea A
(C = 0.8)
(ha) |
Subarea B
(C = 0.4)
(ha) |
Σ(CA) |
Qp
(m3/s) |
| 10 |
160.0 |
60 |
40 |
64 |
28.44 |
| 20 |
126.4 |
60 |
80 |
80 |
28.09 |
| 30 |
106.0 |
60 |
120 |
96 |
28.27 |
| 40 |
92.1 |
60 |
160 |
112 |
28.65 |
| 50 |
82.0 |
60 |
200 |
128 |
29.16 |
| 60 |
74.2 |
60 |
240 |
144 |
29.68 |
|
The fraction of subarea B contributing to peak runoff increases
linearly with rainfall duration.
Therefore: Qp = Σ(CA), in m3/s.
The 25-y peak runoff is the maximum value, corresponding to a 60-min
duration:
Qp = 29.68 m3/s. ANSWER.
|
- Rain falls on a 150-ha composite catchment, which drains two subareas, as follows:
- Subarea A, steep, draining 30%, with time of concentration 20 min; and
- Subarea B, milder steep, draining 70%, with time of concentration 60 min.
The hydrologic abstraction is given in terms of φ = 25 mm/h. Calculate the 100-y-frequency peak flow. Use the following IDF function:
650T 0.22
I = _______________
(tr + 18) 0.75
| |
in which I = rainfall intensity in millimeters per hour, T = return period in years, and tr = rainfall duration in minutes. Assume linear flow concentration at the catchment outlet. State any other assumptions used.
|
Assume runoff concentration without diffusion, and use Eq. 4-12 in the rational formula:
Qp = Ie ΣA = (I - φ) ΣA.
Several rainfall durations are tried, as shown in the following table.
tr
(min) |
I
(mm/h) |
Ie
(mm/h) |
Subarea A
(ha) |
Subarea B
contribution
(ha) |
Σ(A |
Qp
(m3/s) |
| 20 |
70.48 |
45.48 |
45 |
35.0 |
80.0 |
10.11 |
| 30 |
59.15 |
34.15 |
45 |
52.5 |
97.5 |
9.25 |
| 40 |
51.33 |
26.33 |
45 |
70.0 |
115.0 |
8.41 |
| 50 |
45.55 |
20.55 |
45 |
87.5 |
132.5 |
7.56 |
| 60 |
41.10 |
16.10 |
45 |
105.0 |
150.0 |
6.71 |
|
The fraction of subarea B contributing to peak runoff increases linearly with rainfall duration.
Therefore: Qp = Ie ΣA in m3/s.
The 10-y peak flow is the maximum value, corresponding to a 20-min duration:
Qp = 10.11 m3/s. ANSWER.
|
Rain falls on a composite catchment, which drains two subareas, as follows:
- Subarea A, draining 84 ha, C = 0.4, time of concentration 30 min;
- Subarea B, draining 180 ha, C = 0.6, time of concentration 60 min.
The runoff concentration for subarea B is a nonlinear function expressed as follows:
% of time
of concentration |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
% of maximum
discharge |
0 |
5 |
10 |
20 |
30 |
50 |
70 |
80 |
90 |
95 |
100 |
|
Calculate the 50-yr-frequency peak flow. Use the following IDF function:
52T 0.24
I = ______________
(tr + 22) 0.8
| |
in which I = rainfall intensity in millimeters per hour, T = return period in years, and tr = rainfall duration in minutes.
|
Several rainfall durations are tried, ranging from 30 to 60 min, as shown in the following table.
tr
(min) |
I
(cm/h) |
Subarea A
(C = 0.4)
(ha) |
Subarea B
(C = 0.6) |
Σ(CA) |
Qp
(m3/s) |
tr / tc
|
Contribution
(ha) |
| 30 |
5.64 |
84 |
0.500 |
90 |
87.6 |
13.72 |
| 40 |
4.90 |
84 |
0.667 |
138 |
116.4 |
15.84 |
| 50 |
4.34 |
84 |
0.833 |
165 |
132.6 |
16.00 |
| 60 |
3.91 |
84 |
1.000 |
180 |
141.6 |
15.38 |
|
Qp = I Σ(CA), in m3/s.
The 50-y peak flow is the maximum value,corresponding to a 50-min duration:
Qp = 16.0 m3/s. ANSWER.
|
A developed catchment is divided into five subareas, as sketched in Fig. 4-10, with the following data:
| Collection Point |
Subarea Increment
(ha) |
Travel Time
(min) |
C |
| A |
25 |
10 |
0.6 |
| B |
40 |
15 |
0.6 |
| C |
60 |
20 |
0.5 |
| D |
50 |
25 |
0.5 |
| E |
25 |
20 |
0.4 |
|
Calculate the 10-y-frequency peak flow. Use the following IDF function:
500T 0.18
I = _______________
(tr + 20) 0.78
| |
in which I = rainfall intensity in millimeters per hour, T = return period in years, and tr = rainfall duration in minutes.
|
The calculations are summarized in the following table.
Point
|
Subarea
increment
A
(ha) |
Travel
time
(min) |
C
|
Cumulative
travel time
(min) |
Rainfall
intensity
I
(mm/h) |
CA
|
Σ(CA)
|
Qp
(m3/s) |
| A |
25 |
10 |
0.6 |
10 |
53.31 |
15 |
15 |
2.22 |
| B |
40 |
15 |
0.6 |
25 |
38.86 |
24 |
39 |
4.21 |
| C |
60 |
20 |
0.5 |
45 |
29.17 |
30 |
69 |
5.59 |
| D |
50 |
25 |
0.5 |
70 |
22.63 |
25 |
94 |
5.91 |
| E |
25 |
20 |
0.4 |
90 |
19.35 |
10 |
104 |
5.59 |
|
At each point, Qp = I Σ(CA), in m3/s.
The 10-y peak is the maximum value, corresponding to point D: Qp = 5.91 m3/s. ANSWER.
|
A developed catchment is divided into five subareas, as sketched in Fig. 4-10, with the following data:
| Collection Point |
Subarea Increment
(ha) |
Travel Time
(min) |
C |
| A |
15 |
5 |
0.7 |
| B |
30 |
10 |
0.6 |
| C |
20 |
15 |
0.4 |
| D |
10 |
15 |
0.7 |
| E |
15 |
15 |
0.9 |
|
Calculate the 10-y-frequency peak flow. Use the following IDF function:
750T 0.2
I = ______________
( tr + 25) 0.7
| |
in which I = rainfall intensity in millimeters per hour, T = return period in years, and tr = rainfall duration in minutes.
|
The calculations are summarized in the following table.
Point
|
Subarea
increment
A
(ha) |
Travel
time
(min) |
C
|
Cumulative
travel time
(min) |
Rainfall
intensity
I
(mm/h) |
CA
|
Σ(CA)
|
Qp
(m3/s) |
| A |
15 |
5 |
0.7 |
5 |
95.69 |
10.5 |
10.5 |
2.79 |
| B |
30 |
10 |
0.6 |
15 |
78.24 |
18.0 |
28.5 |
6.19 |
| C |
20 |
15 |
0.4 |
30 |
62.60 |
8.0 |
36.5 |
6.35 |
| D |
10 |
15 |
0.7 |
45 |
52.88 |
7.0 |
43.5 |
6.39 |
| E |
15 |
15 |
0.9 |
60 |
46.16 |
13.5 |
57.0 |
7.31 |
|
At each point, Qp = I Σ(CA), in m3/s.
The 5-y peak is the maximum value, corresponding to point E: Qp = 7.31 m3/s. ANSWER.
|
The length of an overland flow plane is L = 90 m. Determine the equilibrium outflow
corresponding to a rainfall excess i = 35 mm/h.
|
Using Eq. 4-19:
qe = (35 mm/h × 90 m × 0.001 m/mm × 1000 L/m3) / (3600 s/h) =
qe = 0.875 L/s/m. ANSWER.
|
An overland flow plane is 100 m long and 200 m wide, with time to equilibrium equal to 1 h.
Estimate the equilibrium storage volume (in cubic meters) for a rainfall excess i = 54 mm/h.
|
Using Eq. 4-19:
qe = (54 mm/h × 100 m × 0.001 m/mm × 1000 L/m3) / (3600 s/h)= 1.5 L/s/m.
Using Eq. 4-20:
Se = (1.5 L/s/m × 1 h × 3600 s/h) / 2 = 2700 L/m.
For a plane 200-m wide:
Se = 2700 L/m × 200 m × 0.001 m3/L = 540 m3. ANSWER.
|
Use the storage concept to calculate the time to equilibrium for an overland flow plane with the following characteristics:
100% laminar flow, plane length L = 75 m, plane slope So = 0.01, rainfall excess i = 72 mm/h, water temperature 20°C.
|
The kinematic viscosity is: v = 1 × 10-6 m2/s.
Using Eq. 4-27:
CL = (9.81 m/s2 × 0.01) / (3 × 1 × 10-6 m2/s) = 32,700 m-1s-1.
The rainfall excess in m/s is:
i = (72 mm/h × 0.001 m/mm) / (3600 s/h) = 0.00002 m/s.
Using Eq. 4-28, the time to equilibrium is:
te = (2 × 751/3) / (0.000022/3 × 32,7001/3) = 358 s.
te = 358 / (60 s/min) = 5.97 min. ANSWER.
|
Calculate the mean overland flow depth (at equilibrium) under a laminar flow regime for a plane length L = 80 m,
rainfall excess i = 30 mm/h, and plane slope So = 0.012. Use water temperature T = 15°C. What would be the mean overland flow depth if the water temperature increased to 25°C?
|
Using Eq. 4-19, the equilibrium outflow is:
qe = iL / 3600 = (30 mm/h × 80 m × 0.001 m/mm × 1000 L/m3) / (3600 s/h)
qe = 0.6666 L/s/m = 0.6666 × 10-3 m3/s/m = 0.0006666 m2/s.
For T = 15°C, v = 1.14 × 10-6 m2/s (Table A-1).
Using Eq. 4-27:
CL = (9.81 m/s2 × 0.012) / (3 × 1.14 × 10-6 m2/s) = 34,421 m-1s-1
In Eq. 4-25, for laminar flow, b = CL, and m = 3. Therefore:
he = (qe CL )1/3 = (0.0006666 / 34,421)1/3 = 0.00269 m = 2.69 mm. ANSWER.
For T = 25°C, v = 0.893 × 10-6 m2/s.
Using Eq. 4-27: CL = 43,942 m-1s-1.
Therefore, with Eq. 4-25:
he = 0.00248 m = 2.48 mm. ANSWER.
|
Use the storage concept to calculate the time to equilibrium for an overland flow plane with the following characteristics:
turbulent Manning friction with n = 0.06, plane length L = 50 m, plane slope So = 0.02, rainfall excess i = 72 mm/h.
|
The rainfall excess in m/s is:
i = (72 mm/h × 0.001 m/mm) / (3600 s/h) = 0.00002 m/s.
In Eq. 4-29, use m = 5/3 for turbulent Manning friction in wide
channels (overland flow plane):
te = [2 × (0.06 × 50)3/5] / (0.000022/5 × 0.023/10) = 947.5 s.
te = 947.5 s / (60 s/min) = 15.8 min. ANSWER.
|
Calculate the rising limb of an overland flow hydrograph using Horton's equation (Eq. 4-37) assuming 75% turbulent flow.
Use: Manning n = 0.06, plane length L = 60 m, plane slope So = 0.015, rainfall excess i = 30 mm/h.
|
The rainfall excess in m/s is:
i = (30 mm/h × 0.001 m/mm) / (3600 s/h) = 0.0000083333 m/s.
qe = 0.0000083333 m/s × 60 m = 0.0005 m3/s/m = 0.5 L/s/m.
For 75% turbulent flow, m = 2.
Therefore, in Eq. 4-29:
te = [2 × (0.06 × 60)1/2 / (0.00000833331/2 × 0.0151/4) = 3756 s.
Using Eq. 4-38, the rising limb of the overland flow hydrograph is
calculated as shown in the following table. ANSWER.
t /te
|
q /qe
|
t
(s) |
q
(L/s/m) |
| 0.1 |
0.039 |
375.6 |
0.0195 |
| 0.2 |
0.144 |
751.2 |
0.0720 |
| 0.3 |
0.288 |
1126.8 |
0.1440 |
| 0.4 |
0.441 |
1502.4 |
0.2205 |
| 0.5 |
0.580 |
1878.0 |
0.2900 |
| 0.6 |
0.695 |
2253.6 |
0.3475 |
| 0.7 |
0.784 |
2629.2 |
0.3920 |
| 0.8 |
0.850 |
3004.8 |
0.4250 |
| 0.9 |
0.896 |
3380.4 |
0.4480 |
| 1.0 |
0.929 |
3756.0 |
0.4645 |
|
|
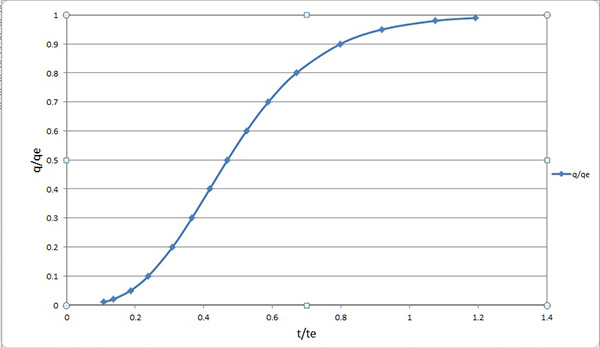
Calculate the rising limb of an overland flow hydrograph using Izzard's equation
(Eq. 4-39). Use: L = 60 m, So = 0.015, i = 30 mm/h, and ν = 1 cs (water temperature T = 20°C).
|
The rainfall excess in m/s is:
i = (30 mm/h × 0.001 m/mm) / (3600 s/h) = 0.0000083333 m/s.
qe = 0.0000083333 m/s × 60 m = 0.0005 m3/s/m = 0.5 L/s/m.
For laminar flow, m = 3.
From Eq. 4-27:
CL = (9.81 × 0.015)/(3 × 0.01 × 10-4) = 49050 m-1s-1
Therefore, in Eq. 4-28:
te = [2 × (60)1/3 / (0.00000833332/3 × 490501/3)] = 520.39 s.
Using Eq. 4-39, the rising limb of the overland flow hydrograph is calculated as shown in the following table and plotted in Fig. M-4-1. ANSWER.
q /qe
|
t /te
|
q
(L/s/m) |
t
(s) |
| 0.01 |
0.108 |
0.005 |
56.1983 |
| 0.02 |
0.1364 |
0.01 |
70.9850 |
| 0.05 |
0.1866 |
0.025 |
97.0903 |
| 0.1 |
0.2382 |
0.05 |
123.9767 |
| 0.2 |
0.3090 |
0.10 |
160.7847 |
| 0.3 |
0.3653 |
0.15 |
190.1007 |
| 0.4 |
0.4171 |
0.20 |
217.0573 |
| 0.5 |
0.4689 |
0.25 |
243.98671 |
| 0.6 |
0.5242 |
0.30 |
272.7965 |
| 0.7 |
0.5880 |
0.35 |
306.0032 |
| 0.8 |
0.6697 |
0.40 |
348.5123 |
| 0.9 |
0.7980 |
0.45 |
415.2523 |
| 0.95 |
0.9194 |
0.475 |
478.4554 |
| 0.98 |
1.0755 |
0.49 |
559.7137 |
| 0.99 |
1.1922 |
0.495 |
620.4171 |
|
|
Fig. M-4-1: Solution of the rising limb using the Izzard Equation.
|
|
Prove that Eqs. 4-37 and 4-38 are equivalent.
|
Eq. 4-37:
t 1 1 + ( q /qe )1/2
____ = ___ ln [ _________________ ]
te 4 1 - ( q /qe )1/2
The definition of inverse hyperbolic tangent is:
1 1 + x
tanh-1 x = ___ ln [ _______ ]
2 1 - x
Substituting x with ( q /qe )1/2 in the formula, Eq. 4-37 becomes:
t /te = (1/2) tanh-1 [( q /qe )1/2]
2 ( t /te ) = tanh-1 [( q /qe )1/2]
tanh [2 ( t /te ) ] = ( q /qe )1/2
q /qe = tanh2 [2 ( t /te )]
|
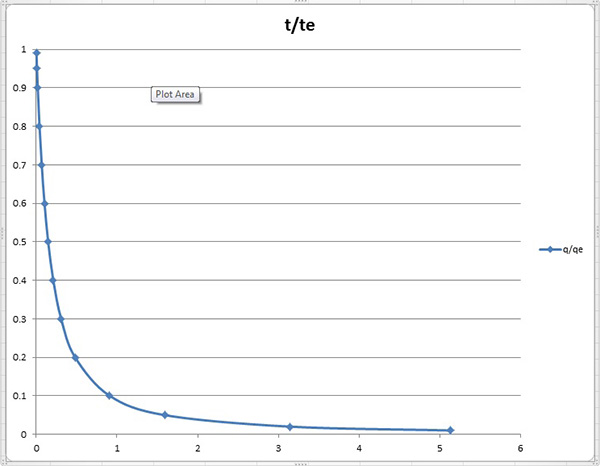
Calculate the receding limb of an overland flow hydrograph, using m = 3, L = 50 m,
So = 0.02, i = 33 mm/h, and ν = 1 cs.
|
The rainfall excess in m/s is:
i = (33 mm/h × 0.001 m/mm) / (3600 s/h) = 0.000009167 m/s.
qe = 0.000009167 m/s × 50 m = 0.00045 m3/s/m = 0.45 L/s/m.
For laminar flow, m = 3.
From Eq. 4-27:
CL = (9.81 × 0.02)/(3 × 0.01 × 10-4) = 65400 m-1s-1
Therefore, in Eq. 4-28:
te = [2 × (50)1/3 / (0.0000091672/3 × 654001/3)] = 417.518 s.
Using Eq. 4-41, the receding limb of the overland flow hydrograph is calculated as shown in the following table and plotted in Fig. M-4-2. ANSWER.
q /qe
|
t /te
|
q
(L/s/m) |
t
(s) |
| 0.01 |
5.136 |
0.0045 |
2144.41 |
| 0.02 |
3.143 |
0.009 |
1312.27 |
| 0.05 |
1.592 |
0.0225 |
664.7 |
| 0.1 |
0.910 |
0.045 |
380.11 |
| 0.2 |
0.481 |
0.09 |
200.83 |
| 0.3 |
0.308 |
0.135 |
128.54 |
| 0.4 |
0.211 |
0.18 |
87.889 |
| 0.5 |
0.147 |
0.225 |
61.313 |
| 0.6 |
0.101 |
0.27 |
42.349 |
| 0.7 |
0.067 |
0.315 |
28.019 |
| 0.8 |
0.040 |
0.36 |
16.742 |
| 0.9 |
0.018 |
0.405 |
7.595 |
| 0.95 |
0.009 |
0.4275 |
3.631 |
| 0.98 |
0.003 |
0.441 |
1.25 |
| 0.99 |
0.002 |
0.446 |
0.835 |
|
|
Fig. M-4-2: Solution of the receding limb using the Izzard Equation.
|
|
Derive the formula for the kinematic time parameter for 100% laminar flow (m = 3).
|
From Eq. 4-53, for 100% laminar flow (m = 3):
tk = he / i = (qe /CL)1/3 / i .
Since: qe = iL, it follows that:
tk = L1/3 / (i 2/3 CL1/3 )
This value is exactly 1/2 of the time-to-equilibrium calculated using the storage concept (Eq. 4-28). ANSWER.
|
Using the formula derived in Problem 4-24, calculate the rising limb of an overland flow hydrograph using the kinematic wave
approach, assuming plane length L = 100 m, plane slope So = 0.01 , rainfall excess i = 25 mm/ h, and water temperature T = 20°C.
|
Using Eq. 4-19, the equilibrium outflow is:
qe = iL / 3600 = (25 × 100) / (3600) = 0.6944 L/s/m
Using Eq. 4-27:
CL = (9.81 m/s2 × 0.01) / (3 × 0.000001 m2/s) = 32,700 m-1s-1
The rainfall excess in m/s is:
i = (25 mm/h × 0.001 m/mm) / (3600 s/h) = 6.944 × 10-6 m/s
Using the formula for the kinematic time parameter (derived in Problem 4-24):
tk = L1/3 / (i 2/3 CL1/3) = 1001/3 / [(6.944 X 10-6)2/3 × (32,700)1/3]
tk = 399 s.
The computations of the rising limb of the kinematic overland flow hydrograph (Eq. 4-52) are summarized in the following table.
t /tk
|
q /qe = (t /tk)3
|
t
(s) |
q
(L/s/m) |
| 0.1 |
0.001 |
39.9 |
0.0007 |
| 0.2 |
0.008 |
79.8 |
0.0055 |
| 0.3 |
0.027 |
119.7 |
0.0187 |
| 0.4 |
0.064 |
159.6 |
0.0444 |
| 0.5 |
0.125 |
199.5 |
0.0868 |
| 0.6 |
0.216 |
239.4 |
0.1500 |
| 0.7 |
0.343 |
279.3 |
0.2382 |
| 0.8 |
0.512 |
319.2 |
0.3555 |
| 0.9 |
0.729 |
359.1 |
0.5062 |
| 1.0 |
1.000 |
399.0 |
0.6944 |
|
|
An overland flow plane has the following characteristics: plane length L = 35 m, plane slope So = 0.008,
Manning n = 0.08, rainfall excess i = 55 mm/ h. Determine if the kinematic wave approximation is applicable to this set of overland flow conditions.
|
The rating curve coefficient for turbulent Manning friction in a wide channel (overland flow plane) is:
b = (1/n) Sol/2. Then: b = 1.118
The rating curve exponent for turbulent Manning friction in a wide channel (overland flow plane) is: m = 5/3. The equilibium flow is:
qe = iL = (55 mm/h × 35 m × 0.001 m/mm) / (3600 s/h) = 0.000535 m3/s/m
Using Eq. 4-50, the equilibrium outflow depth is:
he = (qe/b)3/5 = 0.01 m
The equilibrium mean flow velocity is: ve = qe / he = 0.0535 m/s
The square of the Froude number is:
F 2 = (0.0535)2 / (9.81 × 0.01) = 0.0292
Using Eq. 4-55, the kinematic flow number is:
K = (0.008 × 35 m) / (0.0292 × 0.01 m) = 959
Since K is greater than 20, the kinematic wave approximation is
applicable. ANSWER.
|
Calculate the hydraulic (channel) diffusivity for each of the following two flow conditions:
Bed slope So = 0.005, mean flow depth ho = 0.01 m. and mean velocity uo = 0.05 m/ s; and
Bed slope So = 0.00005, mean flow depth ho = 0.02 m, and mean velocity uo = 0.1 m/ s.
|
Using Eq. 4-61:
(1) vh = (0.05 m/s × 0.01 m) / (2 × 0.005) = 0.05 m2/s. ANSWER.
(2) vh = (0.1 m/s × 0.02 m) / (2 × 0.00005) = 20 m2/s. ANSWER.
|
| http://enghydro.sdsu.edu |
|
150924 12:03 |
|