|
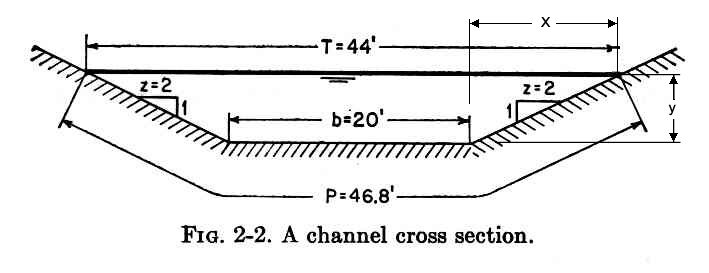
Example 4-2. Compute the critical depth and velocity of the trapezoidal channel shown above, carrying 400 cfs. Solution.- The following proportion holds: z / 1 = x / y From which: x = zy T = b + 2x = b + 2zy A= (1/2) (b + T) y = (1/2) (b + b + 2zy) y = (b + zy) y D = A/T = [(b + zy) y ] / (b + 2 zy) V = Q/A V = (gD)1/2 Q/A = (gD)1/2 Q/(g)1/2 = A(D)1/2 = A(A/T)1/2 Q2/g = A3/T (Q2/g) T - A3 = 0 [Q2/g] (b + 2zyc) - [(b + zyc) yc ]3 = 0 Divide by 8: [Q2/(2g)] (b/4 + zyc/2) - [(b/2 + zyc/2) yc ]3 = 0 For Q = 400 cfs, g = 32.2 ft/s2, b = 20 ft, z = 2: 2484 (5 + yc) - [(10 + yc) yc ]3 = 0 Solve by trial and error: yc = 2.15 ft. Ac = (b + zyc) yc = 52.2 ft2 Vc = Q/Ac = 7.66 fps.
The critical flow equation is:
f(yc) = [Q2/g] (b + 2zyc) - [(b + zyc) yc ]3 = 0 Changing variable to x for simplicity: x = yc f(x) = [Q2/g] (b + 2zx) - [(b + zx) x ]3 = 0
To solve this equation by trial and error, the following simple algorithm is suggested:
Example: onlinechannel02.php
Example 4-4. Using the theory of critical flow, derive an equation for the discharge over a broad-crested weir.
Consider the section on the weir crest where critical flow occurs. The discharge per unit of width is: q = Vc yc q = (gyc)1/2 yc q = (g)1/2 yc3/2 yc = (2/3) He (He = specific energy head at the critical section)
q = (g)1/2 [(2/3) He ]3/2 q = (g)1/2 (2/3)3/2 He 3/2 q = C He 3/2
C = (2/3)3/2 (g)1/2 C = 3.09 in U.S. customary units. C = 1.7 in SI units. This is a theoretical equation, since the critical section is usually difficult to locate with certainty. For practical purposes, the equation is written as:
q = C H3/2 where H is the elevation of the upstream water surface above the weir crest. This assumes that the approach velocity, at a section sufficiently far from the weir, is Va ≈ 0. Therefore: H ≈ He Example: onlinechannel14.php Crossing the El Cora ford on a motorcycle
Go to Chapter 5.
|