|
Q = V A
Q = V A = C A Rx Sy
Q = K Sy
K = C A Rx
Q = K S1/2
K = Q / S1/2
K= C A R1/2
K= (1.486/n) A R2/3
V1 = V2 = V3 = VN = V.
Vi = (1.486/ni) Ri2/3S1/2
Vi = (1.486/ni) (Ai2/3/Pi2/3) S1/2
Ai = Vi3/2 ni3/2 Pi / (1.4863/2 S3/4)
A = V3/2 n3/2 P / (1.4863/2 S3/4)
A = ∑N Ai
V3/2 n3/2 P = ∑N Vi3/2 ni3/2 Pi
V = Vi
n3/2 P = ∑N ni3/2 Pi
n = [∑N( ni3/2Pi) / P ] 2/3
Channels of Compound Section
v1 = (K1/ΔA1) S1/2
v2 = (K2/ΔA2) S1/2
v3 = (K3/ΔA3) S1/2
vN = (KN/ΔAN) S1/2
Q = V A = v1 ΔA1 + v2 ΔA2 + v3 ΔA3 + ... +
vN ΔAN
Q = V A = (K1 + K2 + K3 + ... KN) S1/2
Q = V A = (Σ KN) S1/2
V = (Σ KN) S1/2 / A
α = ∑ v3 ΔA / (V3 A)
β = ∑ v2 ΔA / (V2 A)
α = [ Σ (αN KN3 / ΔAN2) ] /
[(Σ KN)3 / A2 ]
β = [ Σ (βN KN2 / ΔAN) ] /
[(Σ KN)2 / A ]
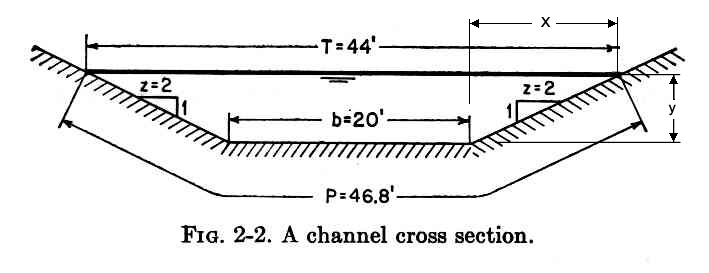
Solution.- The following proportion holds:
z/1 = x/y
From which: x = zy
T = b + 2x = b + 2zy
A= (1/2) (b + T) y = (1/2) (b + b + 2zy) y = (b + zy) y
P = b + 2 (y2 + z2y2) 1/2 = b + 2y (1 + z2)1/2
R = { [(b/2) + (zy)/2] y} / [ (b/2) + y (1 + z2)1/2 ]
Q = (1.486/n) A R2/3 S1/2
(Qn) / (1.486 S1/2) = A R2/3
(Qn) / (1.486 S1/2) = {2[(b/2) + (zy)/2] y} {[(b/2) + (zy)/2]y } 2/3 / [ (b/2) + y (1 + z2)1/2 ]2/3
[(Qn) / (1.486 S1/2)] [ (b/2) + y (1 + z2)1/2 ]2/3 = 2 {[(b/2) + (zy)/2] y } 5/3
[(Qn) / (2 × 1.486 S1/2)] [ (b/2) + y (1 + z2)1/2 ]2/3 = {[(b/2) + (zy)/2] y } 5/3
[(Qn) / (2 × 1.486 S1/2)]3/2 [ (b/2) + y (1 + z2)1/2 ] = {[(b/2) + (zy)/2] y} 5/2
{ [(b/2) + (zy)/2] y} 5/2 - { [(Qn) / (2 × 1.486 S1/2)]3/2 [(1 + z2)1/2]y} -
[(Qn) / (2 × 1.486 S1/2)]3/2 (b/2) = 0
[(Qn) / (2 × 1.486 S1/2)]3/2 = 771.5
(1 + z2)1/2 = 2.236
{ [(b/2) + (zy)/2] y} 5/2 - [(771.5 × 2.236)y] - 771.5 (b/2) = 0
[(10 + y)y]5/2 - 1725y - 7715 = 0
By trial and error:
yn = 3.36 ft.
An = [(b + zyn) yn] = 89.78 ft.
Vn = Q/An = 400/89.78 = 4.46 fps.
The normal flow depth equation is:
f(y) =
{ [(b/2) + (zy)/2] y } 5/2 - { [(Qn) / (2 × 1.486 S1/2)]3/2 [(1 + z2)1/2]y} -
[(Qn) / (2 × 1.486 S1/2)]3/2 (b/2) = 0
f(y) =
{ [(b/2) + (zy)/2] y } 5/2 - { [(Qn) / (2.972 S1/2)]3/2 [(1 + z2)1/2]y} -
[(Qn) / (2.972 S1/2)]3/2 (b/2) = 0
Changing variable to x for simplicity:
f(x) = { [(b/2) + (zx)/2] x } 5/2 - { [(Qn) / (2.972 S1/2)]3/2 [(1 + z2)1/2]x} -
[(Qn) / (2.972 S1/2)]3/2 (b/2) = 0
To solve this equation by trial and error (brute force method), the following simple algorithm is suggested:
Solution by using Newton's approximation:
f(x) = { [(b/2) + (zx)/2] x} 5/2 - { [(Qn) / (2.972 S1/2)]3/2 [(1 + z2)1/2]x} -
[(Qn) / (2.972 S1/2)]3/2 (b/2)
f'(x) = x5/2 (5/2) [(b/2) + (zx)/2] 3/2 (z/2)
+ [(b/2) + (zx)/2] 5/2 (5/2) x3/2
- [(Qn) / (2.972 S1/2)]3/2 (1 + z2)1/2
f'(x) = (5/4) zx5/2 [(b/2) + (zx)/2]3/2
+ (5/2) x3/2 [(b/2) + (zx)/2]5/2
- [(Qn) / (2.972 S1/2)]3/2 (1 + z2)1/2
[When the root xr is approached from the left (xo < xr),
the slope f'(xo) is positive, f(xo) is negative,
and the denominator (xo - xr) is negative].
[When the root xr is approached from the right (xo > xr) (the usual case),
the slope f'(xo) is positive, f(xo) is positive,
and the denominator (xo - xr) is positive].
f'(xo) = f(xo) / (xo - xr)
The root is: xr = xo - f(xo) / f'(xo)
To solve the normal flow depth equation using Newton's approximation, the following algorithm is suggested:
C = (1/n) R1/6
v = C R1/2 S1/2 = (1/n) R2/3 S1/2
v/3.28 = (1/n) (R/3.28)2/3 S1/2
v = (3.28)1/3 (1/n) R2/3 S1/2
v = (1.486/n) R2/3 S1/2
fD = 8g/C2 = 0.113 (R/ks)-1/3
where ks is the linear measure of roughness (grain size).
C = (8g/0.113)1/2 (R/d84)1/6
C = 1.486 R1/6 / (0.031 d841/6)
n = 0.031 d841/6
n = f (R/k) k1/6
n = 0.0342 d501/6
Ku = (1.486/n) Au Ru2/3
Kd = (1.486/n) Ad Rd2/3
K = (KuKd)1/2
Se = F / L
Q = K Se1/2
hu = αu Vu2/(2g) = αu (Q/Au)2/(2g)
hd = αd Vd2/(2g)= αd (Q/Ad)2/(2g)
Se = hf / L = [F + k(hu - hd)] / L
where k = 1 if the reach is contracting (Vu < Vd), and k = 0.5 is the reach is expanding (Vu > Vd),.
The reduction in k accounts for the recovery of the flow during expansion.
Q = K Se1/2
Local man showing water level reached by flood, Kanakumbe, Karnataka, India, December 1991.
τ = γ (ym - y) S
τ = μ (dv/dy)
μ (dv/dy) = γ (ym - y) S
dv = (γ/μ) (ym - y) S dy
γ = ρg
μ = ρν
dv = (gS/ν) (ym - y) dy
v = ∫ dv = ∫ (gS/ν) (ym - y) dy
v = (gS/ν) [ (ymy) - (y2/2) ] + C
v = (gS/ν) [ (ymy) - (y2/2) ]
q = ∫ vdy = (gS/ν) ∫ [ (ymy) - (y2/2) ] dy
q = (gS/ν) [ (ym3/2) - (ym3/6) ]
q = (gS/ν) [ (1/3)ym3 ]
q = [ (gS)/(3ν) ] ym3 = CL ym3
CL = (gS)/(3ν)
v = q/ym = [(gS)/(3ν)] ym2 = CL ym2
q = v ym = (1.486/n) S1/2 ym5/3
q = v ym = C S1/2 ym3/2
V = (β - 1)U/(gD)1/2
where β is the exponent of the rating and U is the mean velocity.
V = 2U/(gD)1/2 = 2 F
V = (1/2)U/(gD)1/2 = (1/2) F
V = (2/3)U/(gD)1/2 = (2/3) F
|