CIVE 530 - OPEN-CHANNEL HYDRAULICS
LECTURE 8B: GRADUALLY VARIED FLOW II

8.3 CHARACTERISTICS OF FLOW PROFILES

The gradually varied flow equation for hydraulically wide channels is:

S_y/S_c = [(S_o/S_c) - F²] / (1 - F²)

In the LHS of the gradually varied flow equation, S_c is always positive, because friction cannot be zero or negative.
Therefore, the sign of the LHS will be that of S_y.
The sign of the LHS can be either of three (3) possibilities:

Positive: RETARDED FLOW (BACKWATER).
Zero: UNIFORM FLOW (NORMAL).
Negative: ACCELERATED FLOW (DRAWDOWN).

In the RHS, there are three (3) possibilities for the numerator:

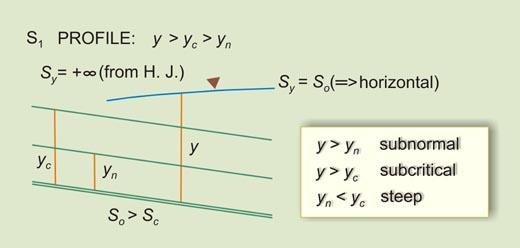
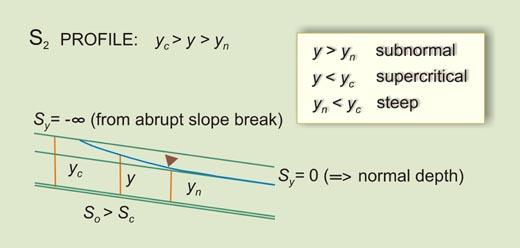
(S_o/S_c) > F² -----> SUBNORMAL
(S_o/S_c) = F² -----> NORMAL
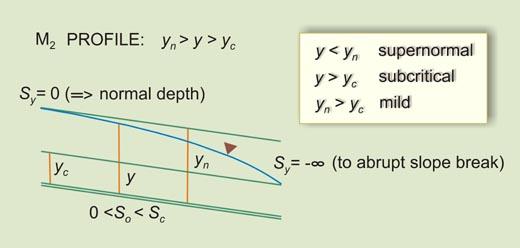
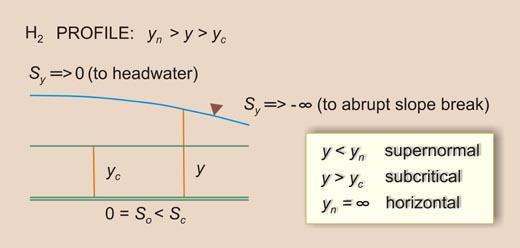
(S_o/S_c) < F² -----> SUPERNORMAL

In the RHS, there are three (3) possibilities for the denominator:

1 > F² -----> SUBCRITICAL
1 = F² -----> CRITICAL (the equation is undefined)
1 < F² -----> SUPERCRITICAL

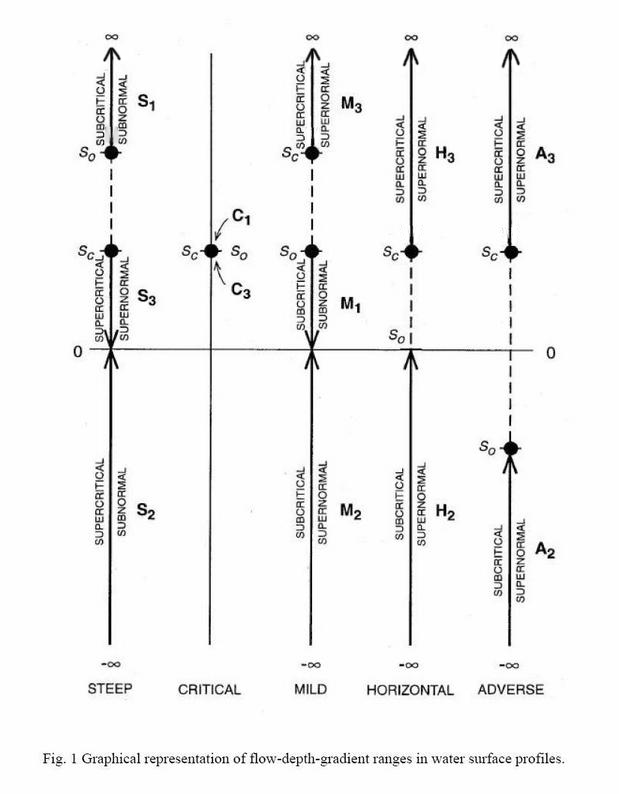
There are three types of families of profiles:

Type I: Positive.
Both numerator and denominator are positive -----> subnormal/subcritical flow -----> RETARDED FLOW.
Type II: Negative.
A. Numerator is positive and denominator is negative -----> subnormal/supercritical flow -----> ACCELERATED FLOW.
B. Numerator is negative and denominator is positive -----> supernormal/subcritical flow -----> ACCELERATED FLOW.
Type III: Positive.
Both numerator and denominator are negative -----> supernormal/supercritical flow -----> RETARDED FLOW.

In a Type I family (subnormal/subcritical), the rule is:

1 > F² < (S_o/S_c)

which is the same as:

(S_o/S_c) > < 1

(S_o/S_c can be greater, equal to, or less than 1)
In the Type I family, there are three profiles:

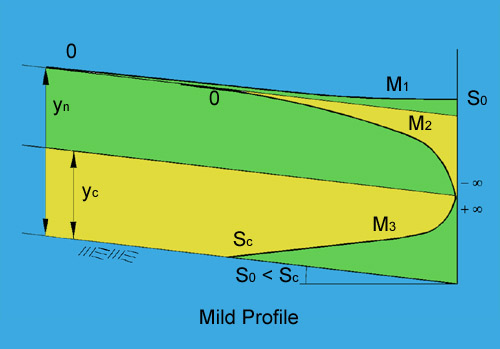
M₁ -----> S_o < S_c    [1]

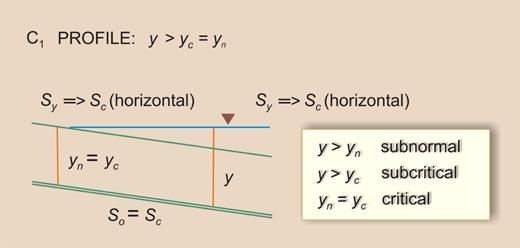
C₁ -----> S_o = S_c    [2]

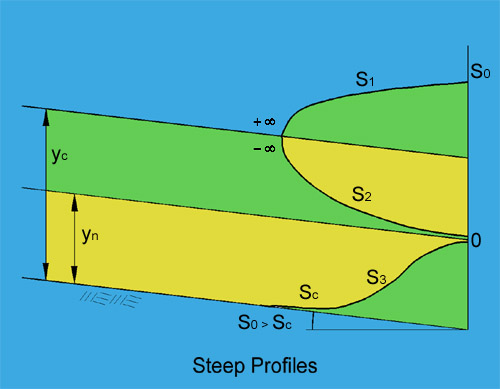
S₁ -----> S_o > S_c    [3]

In a Type I family, there are not horizontal or adverse profiles because:

(S_o/S_c) > F² > 0

Therefore:

S_o > 0

In a Type IIA family (subnormal/supercritical), the rule is:

1 < F² < (S_o/S_c)

which is the same as:

(S_o/S_c) > 1

(S_o/S_c can only be greater than 1)
In the Type IIA family, there is one profile:

S₂ -----> S_o > S_c    [4]

In a Type IIA family, there are not horizontal or adverse profiles because:

(S_o/S_c) > F² > 0

Therefore:

S_o > 0

In a Type IIB family (supernormal/subcritical), the rule is:

1 > F² > (S_o/S_c)

which is the same as:

(S_o/S_c) < 1

(S_o/S_c can only be less than 1)
In the Type IIB family, there are three profiles:

M₂ -----> 0 < S_o < S_c    [5]

H₂ -----> 0 = S_o < S_c    [6]

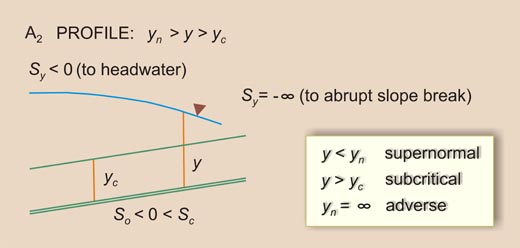
A₂ -----> S_o < 0 < S_c    [7]

In a Type III family (supernormal/supercritical), the rule is:

1 < F² > (S_o/S_c)

which is the same as:

(S_o/S_c) >< 1

(S_o/S_c can be greater, equal to, or less than 1)
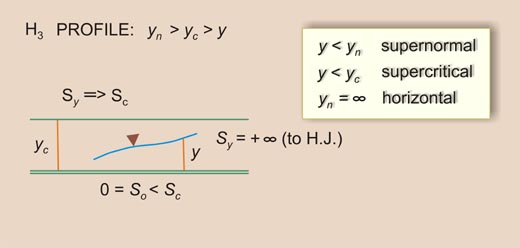
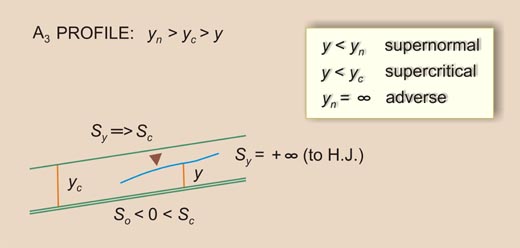
In the Type III family, there are five profiles:

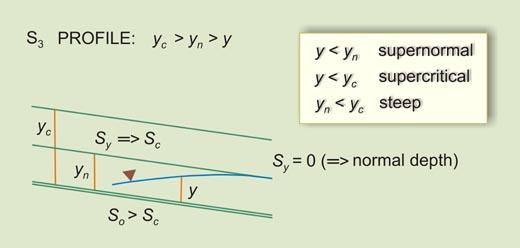
S₃ -----> S_o > S_c    [8]

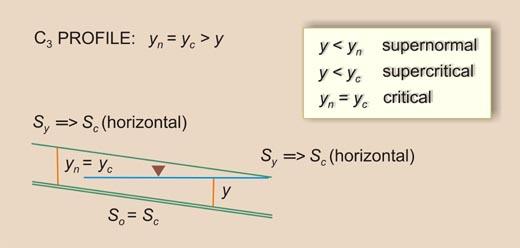
C₃ -----> S_o = S_c    [9]

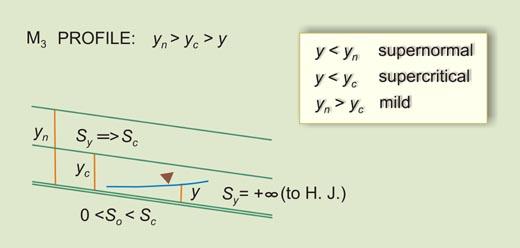
M₃ -----> 0 < S_o < S_c    [10]

H₃ -----> 0 = S_o < S_c    [11]

A₃ -----> S_o < 0 < S_c    [12]

Table 1. Summary of water surface profiles
Family Character Rule S_o/S_c > 1 S_o/S_c = 1 S_o/S_c < 1 S_o = 0 S_o < 0

I Retarded
(Backwater) 1 > F² < (S_o/S_c) S₁ C₁ M₁ - -

IIA Accelerated
(Drawdown) 1 < F² < (S_o/S_c) S₂ - - - -

IIB Accelerated
(Drawdown) 1 > F² > (S_o/S_c) - - M₂ H₂ A₂

III Retarded
(Backwater) 1 < F² > (S_o/S_c) S₃ C₃ M₃ H₃ A₃

8.4 LIMITS TO THE WATER SURFACE PROFILES

The flow depth gradient is:

dy/dx = (S_o - S_c F²) / (1 - F²)

S_y = (S_o - S_c F²) / (1 - F²)

S_y (1 - F²) = S_o - S_c F²

S_y - S_y F² = S_o - S_c F²

F² = (S_o - S_y) / (S_c - S_y)

For uniform flow: S_y = 0. The previous equation leads to:

S_o = S_c F²

For gradually varied flow, the equation remains:

F² = (S_o - S_y) / (S_c - S_y)

There are three cases:

I.   F² > 0
II.   F² = 0
III.   F² < 0

Case I (F² > 0) occurs when:

S_o > S_y and S_c > S_y
The following inequality is satisfied: S_o > S_y < S_c
S_o < S_y and S_c < S_y
The following inequality is satisfied: S_o < S_y > S_c
We conclude that S_y has to be either less than both S_o and S_c, or greater than both.
Case II (F² = 0) leads to S_o = S_y

S_o = (z₁ - z₂)/L

S_y = (y₂ - y₁)/L

(z₁ - z₂)/L = (y₂ - y₁)/L

z₁ + y₁ = y₂ + z₂

This depicts a reservoir.

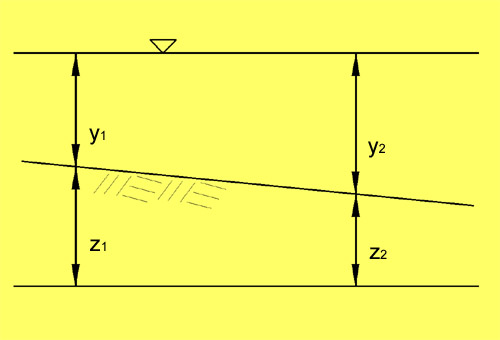
A reservoir.

Case III (F² < 0) is impossible:

S_o > S_y and S_y > S_c
The following inequality is NOT satisfied: S_o > S_y > S_c
S_o < S_y and S_c > S_y
The following inequality is NOT satisfied: S_o < S_y < S_c
We conclude that S_y cannot be less than one and greater than the other slope (S_o and/or S_c).
S_y has to be either less than both S_o and S_c, or greater than both (see Case I).

Case I (F² > 0) can have three subcases:

F² < 1 -----> S_o - S_y < S_c - S_y
Leads to: S_o < S_c    subcritical flow

F² = 1 -----> S_o - S_y = S_c - S_y
Leads to: S_o = S_c    critical flow

F² > 1 -----> S_o - S_y > S_c - S_y
Leads to: S_o > S_c    supercritical flow

Table 2. Behavior of depth gradient S_y.

Channel
slope RETARDED (BACKWATER), S_y is positive,
decreasing in the direction of computation Type Name

S_o < S_c S_y will decrease U/S from S_o (Horizontal) to 0 (Asymptotic to flow) I M₁

S_o < S_c S_y will increase D/S from S_c (More than horizontal) to +∞ (Vertical) III M₃

S_o < S_c S_y will increase D/S from S_c (More than horizontal) to +∞ (Vertical) III H₃

S_o < S_c S_y will increase D/S from S_c (More than horizontal) to +∞ (Vertical) III A₃

S_o = S_c S_y will be constant and equal to S_o = S_c I C₁

S_o = S_c S_y will be constant and equal to S_o = S_c III C₃

S_o > S_c S_y will increase U/S from S_o (Horizontal) to +∞ (Vertical) I S₁

S_o > S_c S_y will decrease D/S from S_c (Less than horizontal) to 0 (Asymptotic to flow) III S₃

Channel
slope ACCELERATED (DRAWDOWN), S_y is NEGATIVE,
increasing in the direction of computation Type Name

S_o > S_c S_y will increase D/S from -∞ (Vertical) to 0 (Asymptotic to flow) IIA S₂

S_o < S_c S_y will increase U/S from -∞ (Vertical) to 0 (Asymptotic to flow) IIB M₂

S_o < S_c S_y will increase U/S from -∞ (Vertical) to S_o = 0 (Asymptotic to flow) IIB H₂

S_o < S_c S_y will increase U/S from -∞ (Vertical) to S_o < 0 (Asymptotic to flow) IIB A₂

Mild water-surface profiles.

Table 3. (a) Occurrence of Water Surface Profiles: Mild channels

M₁ Flow in a mild channel upstream of a reservoir

M₂ Flow in a mild channel, upstream of an abrupt change in grade
(or a steep channel carrying supercritical flow)

M₃ Flow in a mild channel, downstream of a steep channel carrying supercritical flow

Steep water-surface profiles.

Table 3. (b) Occurrence of Water Surface Profiles: Steep channels

S₁ Flow in a steep channel upstream of a reservoir

S₂ Flow in a steep channel, downstream of a mild channel carrying subcritical flow

S₃ Flow in a steep channel, downstream of a steep channel carrying supercritical flow

8.5 METHODOLOGIES TO CALCULATE WATER SURFACE PROFILES

There are two methods to calculate water-surface profiles:
the direct step method,
the standard step method.
These are compared in the following table.

Table 4. Comparison between direct step and standard step methods.

No. Characteristic Direct step method Standard step method

1 Ease of computation Easy (hours) Difficult (months)

2 Type of cross section prismatic any (prismatic or nonprismatic)

3 Independent variable flow depth length of channel

4 Dependent variable length of channel flow depth

5 Calculation advances -> directly by iteration (trial and error)

6 Accuracy increases with -> a smaller flow depth increment lesser cross-sectional variability

7 Type of cross-section input one typical cross section (prismatic) many cross sections (nonprismatic)

8 Data needs minimal extensive

9 Tools spread sheet (or programming) HEC-RAS

10 Reliability Answer always possible Answer sometimes not possible (depends on the type of cross-sectional data)

The number or required cross sections depends on:

Channel slope: steeper channels may require more cross sections.
Cross-sectional variability: the cross-sections need to reflect the longitudinal variability.
Cost and project considerations.
Modeling reality: modeling a three-dimensional flow phenomena as a one-dimensional (i.e, longitudinal description only) analog.

Go to Chapter 8C.

081020

Table 2. Behavior of depth gradient S_y.
Channel slope	RETARDED (BACKWATER), S_y is positive, decreasing in the direction of computation	Type	Name
S_o < S_c	S_y will decrease U/S from S_o (Horizontal) to 0 (Asymptotic to flow)	I	M₁
S_o < S_c	S_y will increase D/S from S_c (More than horizontal) to +∞ (Vertical)	III	M₃
S_o < S_c	S_y will increase D/S from S_c (More than horizontal) to +∞ (Vertical)	III	H₃
S_o < S_c	S_y will increase D/S from S_c (More than horizontal) to +∞ (Vertical)	III	A₃
S_o = S_c	S_y will be constant and equal to S_o = S_c	I	C₁
S_o = S_c	S_y will be constant and equal to S_o = S_c	III	C₃
S_o > S_c	S_y will increase U/S from S_o (Horizontal) to +∞ (Vertical)	I	S₁
S_o > S_c	S_y will decrease D/S from S_c (Less than horizontal) to 0 (Asymptotic to flow)	III	S₃
Channel slope	ACCELERATED (DRAWDOWN), S_y is NEGATIVE, increasing in the direction of computation	Type	Name
S_o > S_c	S_y will increase D/S from -∞ (Vertical) to 0 (Asymptotic to flow)	IIA	S₂
S_o < S_c	S_y will increase U/S from -∞ (Vertical) to 0 (Asymptotic to flow)	IIB	M₂
S_o < S_c	S_y will increase U/S from -∞ (Vertical) to S_o = 0 (Asymptotic to flow)	IIB	H₂
S_o < S_c	S_y will increase U/S from -∞ (Vertical) to S_o < 0 (Asymptotic to flow)	IIB	A₂

Table 3. (a) Occurrence of Water Surface Profiles: Mild channels
M₁	Flow in a mild channel upstream of a reservoir
M₂	Flow in a mild channel, upstream of an abrupt change in grade (or a steep channel carrying supercritical flow)
M₃	Flow in a mild channel, downstream of a steep channel carrying supercritical flow

Table 3. (b) Occurrence of Water Surface Profiles: Steep channels
S₁	Flow in a steep channel upstream of a reservoir
S₂	Flow in a steep channel, downstream of a mild channel carrying subcritical flow
S₃	Flow in a steep channel, downstream of a steep channel carrying supercritical flow