|
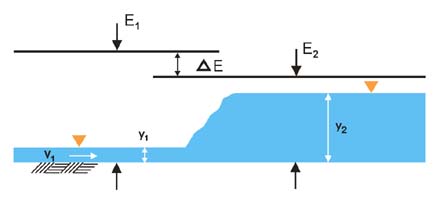
Proof of Eq. 15-1 in "Open-channel hydraulics," by Ven. T. Chow E2/E1 = [(8F12 + 1)3/2 - 4 F12 + 1]/[8F12(2 + F12)]
F1 = v1/(gy1)1/2
F2 = v2/(gy2)1/2
From continuity:
v1y1 = v2y2
v12y12 = v22y22
F12y13 = F22y23
F22 = F12/ (y2/y1)3
Eq. 3-21 (Chow):
y2/y1 = (1/2)[(1 + 8F12)1/2 - 1]
N2 = 1 + 8F12
y2/y1 = (1/2) [N - 1]
2 (y2/y1) = N - 1
(y2/y1)3 = (1/8) [N - 1]3
2 (y2/y1)3 = (1/4) [N - 1]3
N = (1 + 8F12)1/2
N3 = (1 + 8F12)3/2
N2 - 1 = 8F12
F12 = (N2 - 1)/8
4F12 = (N2 - 1)/2
E2/E1 = [y2 + v22/(2g)]/[y1 + v12/(2g)]
E2/E1 = [y2 (1 + F22/2) ]/[y1 (1 + F12/2)]
E2/E1 = 2 (y2/y1) {1 + F12/[2 (y2/y1)3]}/(2 + F12)
E2/E1 = (N - 1){1 + (N2 - 1)/[2 (N - 1)3]}/(2 + F12)
E2/E1 = (N2 - 1)(N - 1) {1 + (N2 - 1) / [2 (N - 1)3]}/[8 F12 (2 + F12) ]
E2/E1 = [(N2 - 1)(N - 1) + (1/2)(N + 1)2]/[8 F12 (2 + F12)]
E2/E1 = {(N3 - N2 - N - 1) + [(N2/2) + N + (1/2)]}/[8 F12 (2 + F12)]
E2/E1 = {(N3 - [(N2 - 1)/2] + 1}/[8 F12 (2 + F12)]
E2/E1 = [(8F12 + 1)3/2 - 4 F12 + 1]/[8F12(2 + F12)]
| ||
|