In 1975, while working on my doctoral dissertation, I came across the method of linear stability, by which a differential equation could be converted to an algebraic equation and solved for a specific case. Sensing that this powerful tool had not been applied to the equations of one-dimensional gradually varied unsteady flow equations (the so-called Saint Venant equations), I asked Dr. Khalid Mahmood, my advisor at the time, for permission to spend time researching this subject, given that it was not directly related to my dissertation. Mahmood inquired whether there was a relation to sediment, since our research project dealt with alluvial river mechanics. I answered that, strictly speaking, this subject was unsteady flow, not alluvial river mechanics. On his advice, I left the subject on the back burner and hurried on to finish my dissertation, which I completed in July of 1976.

Immediately thereafter, I was offered a job as assistant professor of civil engineering at my alma mater, Colorado State University. I sensed an opportunity to discover something of tremendous importance, so I spent the next three months, three hours every evening, applying the method of linear stability to the Saint Venant equations. The effort required a level of mathematical sofistication that proved to be a challenge. The results were published in December of the following year (1977) in the ASCE Journal of the Hydraulics Division.¹ Two years later, in 1979, my coauthor Dr. Daryl B. Simons and I were awarded the prestigious ASCE Karl E. Hilgard Hydraulics Prize, given to the author(s) of the best paper published in the Journal of Hydraulic Engineering in the year prior to the competition.

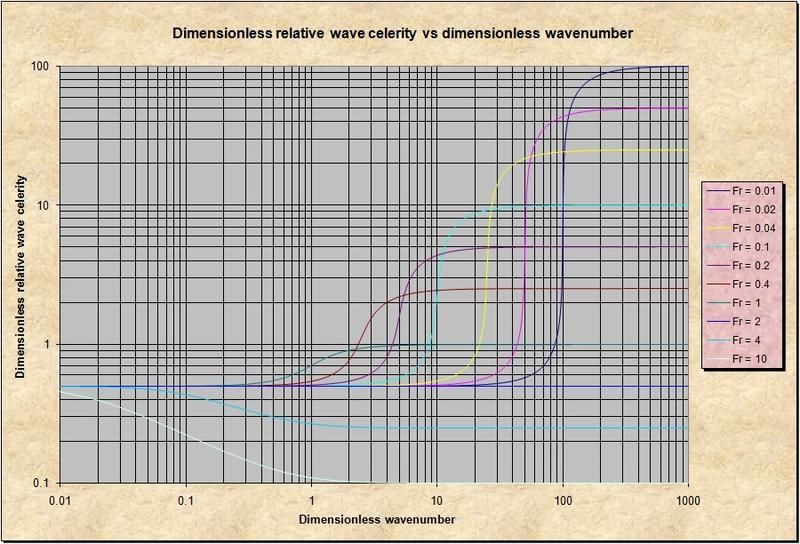
Our findings are summarized in the now famous series of S curves that portray the variation of the dimensionless relative wave celerity as a function of dimensionless wavenumber, for a suitable Froude number set. The S curves depict the progression from kinematic (Seddon) to diffusive, to dynamic, and to inertia-pressure (Lagrangian) waves, throughout the dimensionless "scale" spectrum.

¹ Ponce, V. M., and D. B. Simons. 1977. Shallow wave propagation in open channel flow. ASCE Journal of the Hydraulics Division, Vol. 103, HY12, December, 1461-1476.