OPEN CHANNELS II CHAPTER 4 (2) - ROBERSON ET AL., WITH ADDITIONS CRITICAL FLOW CRITICAL FLOW: SPECIFIC ENERGY IS A MINIMUM. FLOW FOR WHICH DEPTH IS LESS THAN CRITICAL IS TERMED SUPERCRITICAL FLOW. FLOW FOR WHICH DEPTH IS GREATER THAN CRITICAL IS TERMED SUBCRITICAL FLOW. CHARACTERISTICS OF CRITICAL FLOW: CRITICAL FLOW OCCURS WHEN THE SPECIFIC ENERGY IS A MINIMUM FOR A GIVEN DISCHARGE. THE CRITICAL FLOW DEPTH CAN BE SOLVED FROM THE SPECIFIC ENERGY: E = y + V2/(2g) E = y + Q2/(2g A2) CRITICAL FLOW CONDITION: dE/dy = 1 - [Q2/(g A3)] dA/dy = 0 BUT: dA = T dy [Q2Tc/(g Ac3)] = 1 Ac/ Tc = Q2/(g Ac2) Dc = Vc2/ g Vc2/ (g Dc) = 1 F2 = 1 F = 1 F = 1 IN CRITICAL FLOW. EXAMPLE 4-6 DETERMINE THE CRITICAL DEPTH IN A TRAPEZOIDAL CHANNEL FOR A DISCHARGE OF 500 CFS. THE WIDTH OF THE CHANNEL BOTTOM IS 20 FT, AND THE SIDE SLOPE Z = 1. SOLUTION: Q2Tc/(g Ac3)] = 1 Ac3/Tc = Q2/g = 5002/32.2 = 7764 FOR THIS CHANNEL: A = y (b+y) T = b + 2y [yc (b+yc)]3/ (b + 2yc) = 7764 BY ITERATION:   yc = 2.57 FT. A = y (b+y) = 2.57 (20 + 2.57) = 58. V = Q/A = 500/58 = 8.62 FPS. COMPARE WITH ONLINE CALCULATION. RESULT: y = 2.57 FT; V = 8.62 FPS (EXACTLY THE SAME RESULT). IN A RECTANGULAR CHANNEL, THE CRITICAL DEPTH IS SOLELY A FUNCTION OF THE DISCHARGE. Ac/ Tc = Q2/(g Ac2) BECAUSE Ac = yc Tc yc = Q2/(g yc2 Tc2) AND q = Q/Tc yc = [q2/g] 1/3 yc3 = [q2/g] yc3 = [Vc2yc2/g] yc = Vc2/(g) Vc2/(g yc) = 1 F = Vc/(g yc)1/2 = 1 FROUDE NUMBER. THE FROUDE NUMBER IS EQUAL TO 1 WHEN THE FLOW IS CRITICAL. CRITICAL FLOW IS HAS UNSTABLE SURFACE. 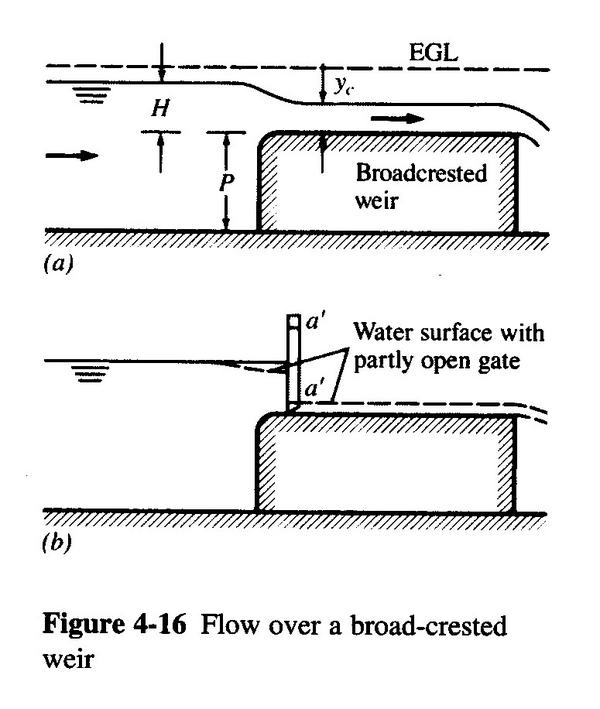OCCURRENCE OF CRITICAL FLOW CRITICAL FLOW OCCURS WHEN A LIQUID PASSES OVER A BROAD-CRESTED WEIR (a) CONSIDER A CLOSED SLUICE GATE THAT PREVENTS WATER FROM BEING DISCHARGED FROM THE RESERVOIR IF THE GATE IS OPENED A SMALL AMOUNT a', THE FLOW WILL BE SUBCRITICAL U/S AND SUPERCRITICAL D/S (b) AS THE GATE IS FURTHER OPENED, A POINT IS REACHED WHERE BOTH DEPTHS U/S AND D/S ARE THE SAME. THIS IS THE CRITICAL CONDITION. BEYOND THIS DEPTH, THE GATE HAS NO INFLUENCE ON THE FLOW. THE FLOW OVER THE BROAD-CRESTED WEIR IS: q = (gyc3)1/2 Q = L (gyc3)1/2 = L g1/2yc3/2 SINCE: V2/(g yc) = 1 THEN: yc/2= V 2/(2g) E = (3/2)yc yc = (2/3) E E = TOTAL HEAD ABOVE CREST: E = H + Va2/(2g) Q = L g1/2yc3/2 = L g1/2 (2/3) 3/2 (Ec) 3/2 FOR HIGH WEIRS, Va ≅ 0; E ≅ H Q = L g1/2 (2/3) 3/2 H 3/2 Q = [2 (1/3)3/2] (2g)1/2 L H 3/2 Q = 0.385 (2g)1/2 L H 3/2 Q = 3.09 L H 3/2 [U.S. CUSTOMARY] Q = 1.7 L H 3/2 [SI UNITS] THIS EQUATION IS THE BASIC THEORETICAL EQUATION FOR A BROAD-CRESTED WEIR. 8000-ft long emergency spillway weir at Boerasirie Conservancy, Guyana. THE BROAD-CRESTED WEIR SHOWN IN THE ABOVE PHOTO WAS DESIGNED WITH C = 1.45 (SI UNITS). Weir at Villa Grande dam, Cuajone, Peru. DISCHARGE IS ALSO INFLUENCED BY HEAD LOSS AND THE SHAPE OF THE WEIR. 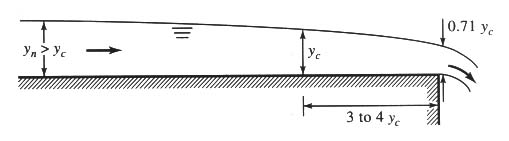FLOW DEPTH PASSES THROUGH CRITICAL STAGE IN CHANNEL FLOW WHERE THE SLOPE CHANGES FROM MILD TO STEEP. EXPERIENCE SHOWS THAT CRITICAL DEPTH OCCURS A VERY SHORT DISTANCE U/S OF THE INTERSECTION OF THE TWO CHANNELS. CRITICAL DEPTH ALSO OCCURS UPSTREAM OF A FREE OVERFALL. CRITICAL DEPTH WILL OCCUR 3 TO 4 DEPTHS U/S OF THE BRINK. CHANNEL TRANSITIONS A TRANSITION IS A STRUCTURE DESIGNED TO CONVEY WATER SMOOTHLY FROM A CONDUIT OF ONE SHAPE TO ANOTHER OF A DIFFERENT SHAPE. A COMMON APPLICATION IS BETWEEN A CANAL AND A FLUME. ALSO, BETWEEN OPEN CHANNELS AND INVERTED SIPHONS. INLET TRANSITION: FROM LARGE TO SMALL. EXPANSION: FROM SMALL TO LARGE. THE SIMPLEST TYPE OF TRANSITION IS A STRAIGHT WALL NORMAL TO THE FLOW DIRECTION (TECHNICALLY THIS IS NOT A TRANSITION). THIS TYPE PRODUCES EXCESSIVE HEAD LOSS. GRADUAL TRANSITIONS ARE USED TO PREVENT EXCESSIVE HEAD LOSSES. 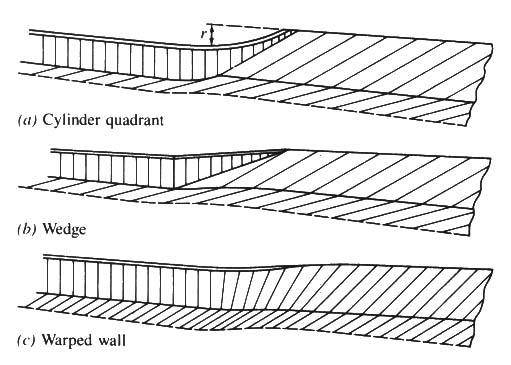THREE COMMON TYPES: -- CYLINDER QUADRANT -- WEDGE -- WARPED WALL ALL THREE ARE FOR INLET TRANSITIONS. LAST TWO ARE SUITED FOR EXPANSIONS. FOR WEDGE TRANSITION, ANGLE θ IS 27.5o DEGREES FOR INLETS, 22.5o FOR EXPANSIONS. FOR WARPED WALL, ANGLE θ IS 12.5o DEGREES FOR BOTH INLETS AND EXPANSIONS. DESIGN OF TRANSITION TO JOIN CANAL AND FLUME NEEDS: -- DEPTH AND VELOCITY ON BOTH FLUME AND CANAL -- WATER SURFACE ELEVATION U/S FOR INLET; D/S FOR EXPANSION. STEP BY STEP PROCEDURE CHOOSE THE TYPE OF TRANSITION (CYLINDER, WEDGE, OR WARPED) FOR INLET, CALCULATE WATER SURFACE ELEVATION D/S. FOR EXPANSION, CALCULATE THE WATER SURFACE ELEVATION U/S. APPLY THE ENERGY EQUATION. 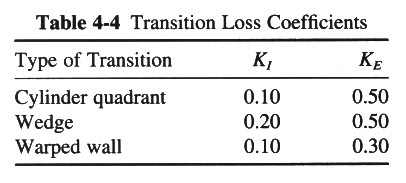FOR INLET, HEAD LOSS IS KIV2/(2g), WHERE V IS THE D/S VELOCITY. KI IS THE HEAD LOSS COEFFICIENT FOR THE TRANSITION. FOR EXPANSION, HEAD LOSS IS KE (V12 - V22)/(2g). KE IS THE HEAD LOSS COEFFICIENT FOR THE EXPANSION. V1 IS THE U/S VELOCITY. V2 IS THE D/S VELOCITY. LOSS COEFFICIENTS IN TABLE 4-4. FOR INLET, CALCULATE THE D/S INVERT ELEVATION. FOR EXPANSION, CALCULATE THE U/S INVERT ELEVATION. INVERT ELEV.= W.S. ELEV. - DEPTH. ESTABLISH INVERT ELEVATIONS ALONG THE TRANSITION BY A STRAIGHT LINE ELEVATION CHANGE BETWEEN U/S AND D/S. ESTABLISH W.S. ELEVATIONS THROUGH THE TRANSITION. USE ENERGY EQUATION. EXAMPLE 4-8 A TRANSITION IS NEEDED BETWEEN A TRAPEZOIDAL CANAL OF DEPTH = 3 FT AND VELOCITY 2.3 FPS, AND A FLUME OF RECTANGULAR SECTION, AND VELOCITY = 5.9 FPS. THE CANAL HAS BOTTOM WIDTH 10 FT AND SIDE SLOPES z = 2H:1V. THE INVERT ELEVATION OF THE CANAL (U/S END OF TRANSITION) IS 1000 FT. DETERMINE THE FLUME DIMENSIONS TO KEEP THE FROUDE NUMBER BELOW 0.5, AND DESIGN A TRANSITION. THE FLUME VELOCITY IS TO BE 5.9 FPS. SOLUTION: LET'S USE A WEDGE TRANSITION. KI = 0.20 (TABLE 4-4). CROSS-SECTIONAL AREA OF THE CHANNEL IS = (10 × 3) + (6 × 3) = 48 SQ FT. DISCHARGE Q = V A = 2.3 X 48 = 110.4 DETERMINE THE FLUME DIMENSIONS: IN FLUME: Q = V A IN RECTANGULAR FLUME, ASSUME: b/d = 1. THEN:   A = d2 d = (Q/V)1/2 V1/2 d = Q1/2 = (110.4)1/2 = 10.5             [1] F = V/(gd)1/2 = 0.5 V = 0.5 (gd)1/2             [2] FROM [1] AND [2], SOLVING FOR d = 4.326 ft. FOR DESIGN: bflume = 4.4 ft. dflume = Q/(bflumeVflume) = 110.4 /(4.4 X 5.9) = 4.25 ft. 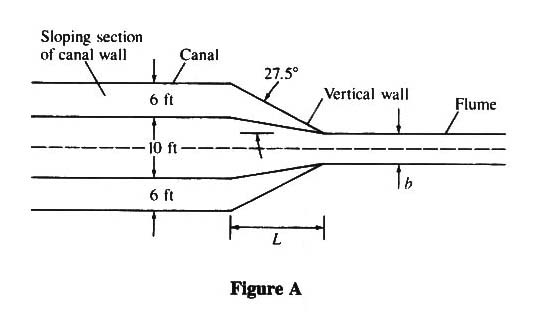LENGTH OF THE TRANSITION tan 27.5o = [Tc/2 - Tf/2] / L = [11 - 2.2] /L L = 8.8 /tan 27.5o = 16.9 FT. FOR DESIGN, ASSUME L = 17 FT. 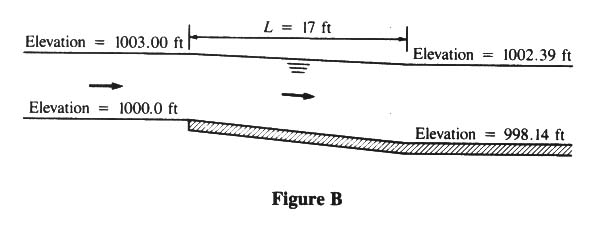DETERMINE THE W. S. ELEV. IN THE FLUME: z1 + y1 + α1V12/(2g) = z2 + y2 + α2V22/(2g) + hL ASSUME α1 = α2 = 1.1 1000 + 3.0 + (1.1) 2.32/(2 × 32.2) = z2 + y2 + (1.1) 5.92/(2 × 32.2) + (0.2) 5.92/(2 × 32.2) z2 + y2 = 1002.39 ft. z2 = 1002.39 - y2 = 1002.39 - 4.25 = 998.14 ft. 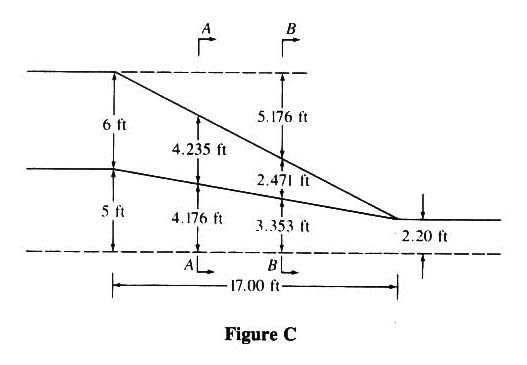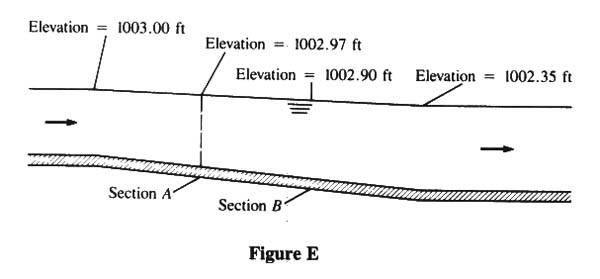NOW CHECK THE VELOCITIES AT SECTIONS A AND B, AT 5 AND 10 FT D/S OF CANAL. FIRST ASSUME A PLANE SURFACE BETWEEN THE U/S AND D/S: dA = 3.00 - (5/17) (1003.00 - 1002.39) + (5/17) (1000.00 - 998.14) = 3.368 ft. dB = 3.00 - (10/17) (1003.00 - 1002.39) + (10/17) (1000.00 - 998.14) = 3.735 ft. 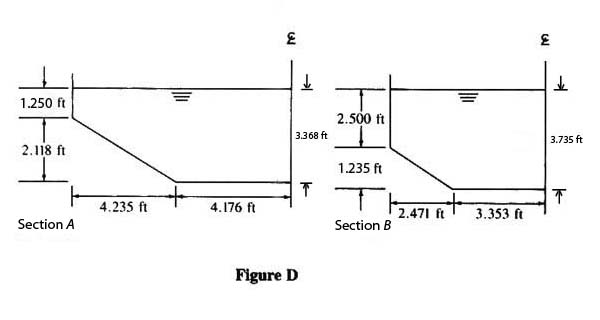VERTICAL DEPTH AT SECTION A: (5/17) × 4.25 = 1.25 VERTICAL DEPTH AT SECTION B: (10/17) × 4.25 = 2.50 THE CROSS-SECTIONAL FLOW AREA AT SECTION A (FIG. D): AA= 2 [ (4.176 X 3.368) + (1.25 X 4.235) + (1/2) (2.118 X 4.235)] = 47.69 SQ.FT. VA = Q/AA = 110.4 / 47.369 = 2.33 FPS. SIMILAR CALCULATIONS FOR B YIELD: AB= 2 [ (3.353 X 3.735) + (2.50 X 2.471) + (1/2) (1.235 X 2.471)] = 40.46 SQ.FT. VB = Q/AA = 110.4 / 40.46 = 2.73 FPS. DETERMINE W.S. ELEV. AT SECTIONS A AND B, ASSUMING HEAD LOSS IS LINEARLY DISTRIBUTED ALONG THE TRANSITION: z1 + y1 + α1V12/(2g) = zA + yA + αAVA2/(2g) + hL (1 → A) 1000 + 3.00 + 1.1 (2.3)2/(64.4) = zA + yA + 1.1 (2.33)2/(64.4) + (5/17) (0.2) (5.9)2/(64.4) zA + yA = 1002.97 FT. z1 + y1 + α1V12/(2g) = zB + yB + αBVB2/(2g) + hL (1 → B) 1000 + 3.00 + 1.1 (2.3)2/(64.4) = zB + yB + 1.1 (2.73)2/(64.4) + (10/17) (0.2) (5.9)2/(64.4) zB + yB = 1002.90 FT. 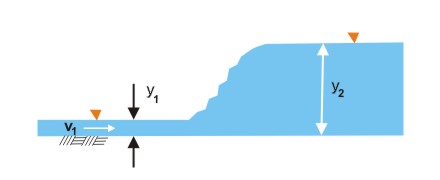THE HYDRAULIC JUMP WHEN THE FLOW IS SUPERCRITICAL UPSTREAM, AND IS THEN FORCED TO BECOME SUBCRITICAL IN A DOWNSTREAM SECTION (DUE TO PREVAILING DEPTH DOWNSTREAM), AN ABRUPT CHANGE IN DEPTH OCCURS, WITH CONSIDERABLE ENERGY LOSS: THE HYDRAULIC JUMP. Hydraulic jump at outlet from Tinajones dam, Peru. 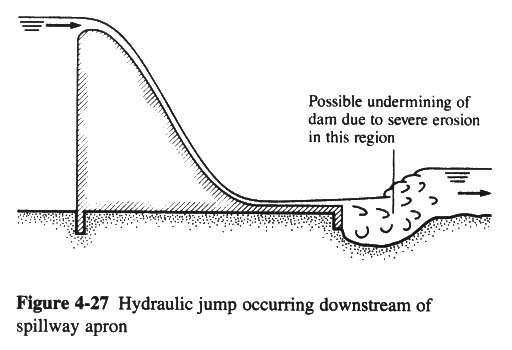MANY SPILLWAYS ARE DESIGNED SO THAT A JUMP WILL OCCUR ON AN APRON OF THE SPILLWAY, THEREBY REDUCING THE DOWNSTREAM VELOCITY AND AVOIDING EROSION. DESIGNER MUST BE SURE THAT SUPERCRITICAL FLOW WILL NOT BECOME SUBCRITICAL PREMATURELY. OVERTOPPING MAY OCCUR IN THIS CASE. ENERGY LOSS IS NOT KNOWN. MOMENTUM IS CONSERVED; MOMENTUM EQUATION IS USED. UNIFORM FLOW OCCURS U/S AND D/S. RESISTANCE OF THE CHANNEL BOTTOM IN SHORT STRETCH IS NEGLIGIBLE. DERIVATION IS FOR A HORIZONTAL CHANNEL, BUT RESULTS SHOW THAT IT IS APPLICABLE TO CHANNELS OF MODERATE SLOPE (S < 0.02). MOMENTUM EQUATION TO CONTROL VOLUME SHOWN IN FIG. 4-24. ∑ Fx = ∑ ρ (V⋅A) V = ∑ ρ Q V FORCES ARE THE HYDROSTATIC FORCES ON EACH END: pa1A1 - pa2A2 = ρQV2 - ρQV1 pa1A1 + ρQV1 = pa2A2 + ρQV2 THIS EQUATION STATES THAT MOMENTUM IS CONSERVED. EXAMPLE 4-9 WATER FLOWS IN A TRAPEZOIDAL CHANNEL AT A RATE OF 300 CFS. THE CHANNEL HAS A BOTTOM WIDTH OF 10 FT AND SIDE SLOPE z = 1. IF A HYDRAULIC JUMP IS FORCED TO OCCUR WHERE THE U/S DEPTH IS 1 FT, WHAT WILL BE THE D/S DEPTH AND VELOCITY? SOLUTION: FOR THE U/S SECTION, THE AREA A1 = 11 SQ FT. THE DEPTH OF THE CENTROID OF A1 IS FOUND TO BE 0.47 FT. THE PRESSURE AT THE CENTROID IS:   62.4 LBS/CU.FT X 0.47 FT = 29.3 LBS/SQ.FT. V1 = Q/A1 = 300/11 = 27.3 FPS. pa1A1 + ρQV1 = pa2A2 + ρQV2 pa1A1 + ρQV1 = 29.3 × 11 + 1.94 × 300 × 27.3 = 16210 pa2A2 + ρQV2 = 16210 γyc2A2 + ρQ2/A2 = 16210 A2 = y2(b + y2) = by2 + y22 yc2 = ∑Aiyci / A2 = [ by2(y2/2) + y22(y2/3)] / [y2(b + y2)] yc2 A2 = [by2(y2/2) + y22(y2/3)] yc2 A2 = y2 [b(y2/2) + y22/3] γy2 [by2/2 + y22/3] + ρQ2/A2 = 16210 γy2 [by2/2 + y22/3] + ρ (90000) / (by2 + y22) = 16210 62.4 y2 [10 y2/2 + y22/3] + 1.94 (90000) / (10 y2 + y22) - 16210 = 0 BY TRIAL AND ERROR: y2 = 5.75 FT A2 = 10 × 5.75 + 5.752 = 90.56 SQ.FT V2 = 300/90.56 = 3.31 FPS. EXAMPLE 4-9 (WITH RECTANGULAR CHANNEL) WATER FLOWS IN A TRAPEZOIDAL CHANNEL AT A RATE OF 300 CFS. THE CHANNEL HAS A BOTTOM WIDTH OF 10 FT AND SIDE SLOPE z = 0. IF A HYDRAULIC JUMP IS FORCED TO OCCUR WHERE THE U/S DEPTH IS 1 FT, WHAT WILL BE THE D/S DEPTH AND VELOCITY? SOLUTION: FOR THE U/S SECTION, THE AREA A1 = 10 SQ FT. THE DEPTH OF THE CENTROID OF A1 IS FOUND TO BE 0.5 FT. THE PRESSURE AT THE CENTROID IS:   62.4 LBS/CU.FT × 0.5 FT = 31.2 LBS/SQ.FT. V1 = Q/A1 = 300/10 = 30 FPS. pa1A1 + ρQV1 = pa2A2 + ρQV2 pa1A1 + ρQV1 = 31.2 × 10 + 1.94 × 300 × 30 = 17772 pa2A2 + ρQV2 = 17772 γyc2A2 + ρQ2/A2 = 17772 A2 = y2 b yc2 = y2/2 γby22/2 + ρQ2/A2 = 17772 γ (5y22) + ρ (90000) / (10 y2) = 17772 62.4 (5 y22) + 1.94 (90000) / (10 y2) - 17772 = 0 312 y22 + 17460 / y2 - 17772 = 0 BY TRIAL AND ERROR: y2 = 7.0 FT A2 = 10 × 7.0 = 70 SQ.FT V2 = 300/70 = 4.29 FPS. Sequent depths in a hydraulic jump. ONLINE VERIFICATION: INPUT: y1= 1; v1 = Q/A1 = 300/(10 × 1) = 30. http://ponce.sdsu.edu/onlinechannel11.php RESULT: y2 = 6.996 FT; V2 = 4.287 FPS. (SAME RESULT). 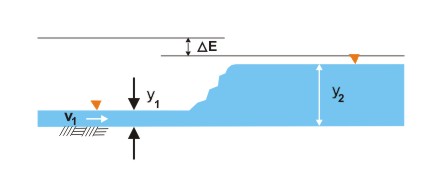HEAD LOSS DUE TO HYDRAULIC JUMP HEAD LOSS IS RELATIVELY LARGE BECAUSE OF INTENSE TURBULENT MIXING. ONE CAN DETERMINE HEAD LOSS WRITING THE ENERGY EQUATION AND SOLVING FOR HEAD LOSS. HYDRAULIC JUMP IN A RECTANGULAR CHANNEL: THE SOLUTION OF MOMENTUM CONSERVATION YIELDS y2 AS A FUNCTION OF y1 AND THE FROUDE NUMBER OF THE U/S FLOW F1. y2 = (y1/2) [(1 + 8 F12)1/2 - 1 ] F1 = V1/ (gy1)1/2 Energy loss ΔE in a hydraulic jump. ONLINE CALCULATION OF ENERGY LOSS IN A HYDRAULIC JUMP: INPUT:   y1 = 1; v1 = Q/A1 = 300/(10 × 1) = 30. http://ponce.sdsu.edu/onlinechannel12.php Result: ΔE = 7.705 FT. ONLINE CALCULATION OF SEQUENTS DEPTHS IF ENERGY LOSS IS KNOWN: INPUT:   ΔE = 7.705 FT; q = Q/b = 300/10 = 30. http://ponce.sdsu.edu/onlinechannel16.php RESULT: y1= 1; y2 = 6.996 FT. 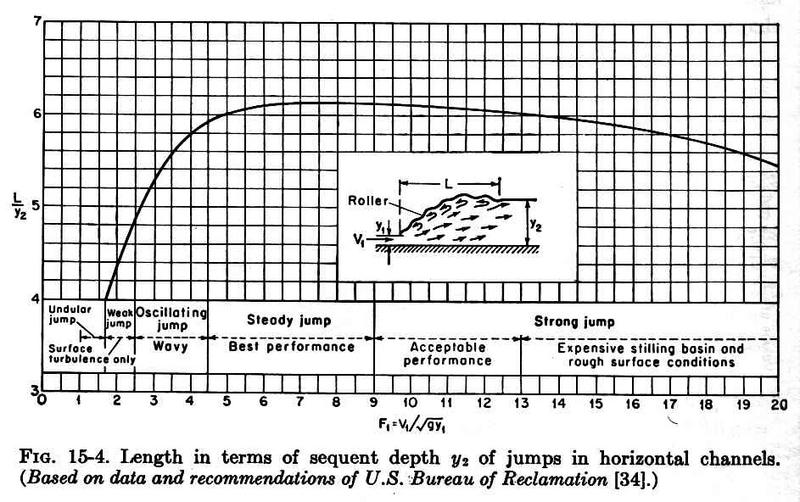LENGTH OF THE HYDRAULIC JUMP THE LENGTH OF THE HYDRAULIC JUMP IS THE DISTANCE MEASURED FROM THE FRONT FACE OF THE JUMP TO A POINT ON THE SURFACE IMMEDIATELY DOWNSTREAM OF THE ROLLER. EXPERIMENTS IN RECTANGULAR CHANNELS SHOW THAT L = 6 y2 FOR 4 < F1 < 16. Energy loss ΔE in a hydraulic jump. OUTSIDE THIS RANGE, THE LENGTH IS SOMEWHAT LESS THAN L = 6 y2. TRANSITION FROM SUPERCRITICAL TO SUBCRITICAL FLOW PRODUCES A HYDRAULIC JUMP. THE RELATIVE HEIGHT OF THE JUMP IS A FUNCTION OF F1. FLOW OVER A SPILLWAY INVARIABLY RESULTS IN SUPERCRITICAL FLOW DOWNSTREAM OF THE SPILLWAY. A HYDRAULIC JUMP FORMS NEAR THE BASE OF THE SPILLWAY. Sheep Creek Barrier Dam, Utah. Turner Dam, San Diego County. THE DOWNSTREAM PORTION OF THE SPILLWAY SHOULD BE DESIGNED SO THAT THE JUMP FORMS ON THE CONCRETE STRUCTURE ITSELF. IF THIS IS NOT THE CASE, EROSION MAY OCCURS DOWNSTREAM OF THE SPILLWAY. 090922