CIV E 444 - APPLIED HYDRAULICS
SPRING 2016
LAB No. 12 SOLUTION
- Do/D1 = 24 / 8 = 3
The pressure coefficient is defined as: V1 = Vo (1 - Cp)1/2
Cp = 1 - (V1/Vo)2 = 1 - (Do/D1)4 = - 80.
The free-vortex incipient cavitation index is: σi, A = 1 - 2 Cp = 1 - [2 × (- 80)] = 161
pv = 37 psf
σi = (po - pv) / (ρVo2 /2)
161 = [(25 × 144 in2/ft2) - 37)] / [ 1.94 Vo2/2]
Vo = 4.78 fps
Q = Vo Ao = Vo (π/4) Do2 = 4.78 (0.7854) (2)2 = 15 cfs.
- D = 40 cm = 0.4 m.
n = 1000 rpm = 1000 / 60 = 16.667 rps
CH = ΔH / [ (D2n2) / g ] = (3 × 9.81) / [(0.4)2 (16.667)2] = 0.662
From the given figure, with CH = 0.662, find CQ = 0.65, and with CQ = 0.65, find CP = 0.54
CQ = Q / (nD3) = 0.65
Q = 0.65 nD3 = 0.65 × 16.667 × (0.4) 3 = 0.693 m3/s
CP = P / (ρ D5 n3)
ρ = 1 KN ⋅ s2/m4
P = 0.54 ρ D5 n3 = 0.54 (1) (0.4)5 (16.667)3 [KN ⋅ m/s]
P = 25.6 KN ⋅ m/s = 25.6 KW
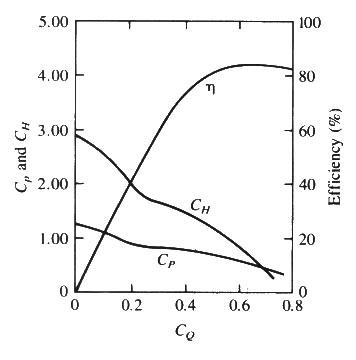
- From the first figure, at maximum efficiency: ΔH = 95 m, and Q = 0.214 m3/s
( CH ) N = ( CH ) N = 2133.5
[ ΔH / (D2n2 / g) ] N = [ ΔH / (D2n2 / g) ] N = 2133.5
[ ΔH / (n2) ] N = [ ΔH / (n2) ] N = 2133.5
70 / N2 = 95 / (2133.5)2
N = 2133.5 (70/95)1/2 = 1882 RPM
(CQ) N = 1882 = (CQ) N = 2133.5
[Q / (nD3)] N = 1882 = [Q / (nD3)] N = 2133.5
QN = 1882 / QN = 2133.5 = 1882 / 2133.5 = 0.883
QN = 1882 = 0.883 QN = 2133.5 = 0.883 × 0.214 = 0.189 m3/s
n = 1882 / 60 = 31.37 rps
D = 0.371 m
CQ = Q / (nD3) = 0.189 / [ 31.37 × (0.371)3 ] = 0.119
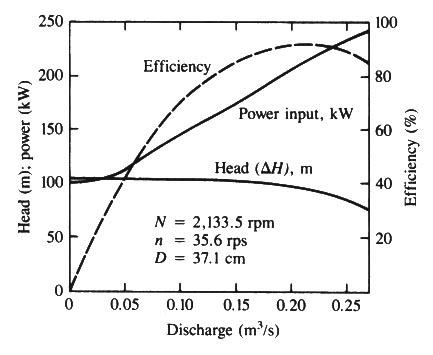
From the second figure: CP = 0.68
CP = P / (ρ D5 n3)
ρ = 1 KN ⋅ s2/m4
P = 0.68 ρ D5 n3 = 0.68 × 1 × (0.371)5 (31.37)3 [KN ⋅ m/ s]
P = 147.5 KN ⋅ m/ s = 147.5 KW
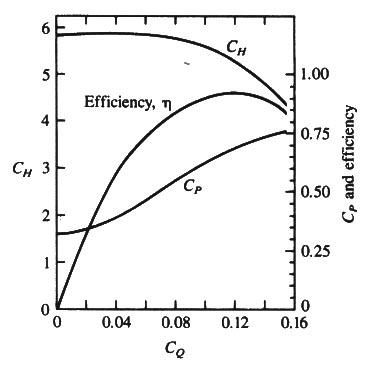
- hp = (z2 - z1) + [V2/(2g)] [f (L/D) + ∑ KL ]
hp = (z2 - z1) + [ Q2/(2gA2)] [ f (L/D) + Ke + Kb + KE ]
From Table 5-3 (in the text): Ke = 0.5; Kb = 0.19; KE = 1
hp = (500 - 450) + [ Q2/(2g ((π/4) D2)2) ] [ 0.016 (2000/0.5) + 0.5 + 0.19 + 1 ]
hp = 50 + [ Q2/(2 (9.81) (π/4)2 (0.5)4 ] (65.69)
hp = 50 + [ Q2/(0.7564) ] (65.69)
hp = 50 + 86.84 Q2
Pump performance curve: H = 70 - 700 Q 2
At H = hp: Q = 0.159 m3/s
hp = 50 + 86.84 (0.159) 2 = 52.207 m.