CIV E 445 - APPLIED HYDROLOGY
SPRING 2003
SOLUTIONS TO HOMEWORK 8 , CHAPTER 6

Problem 8-1

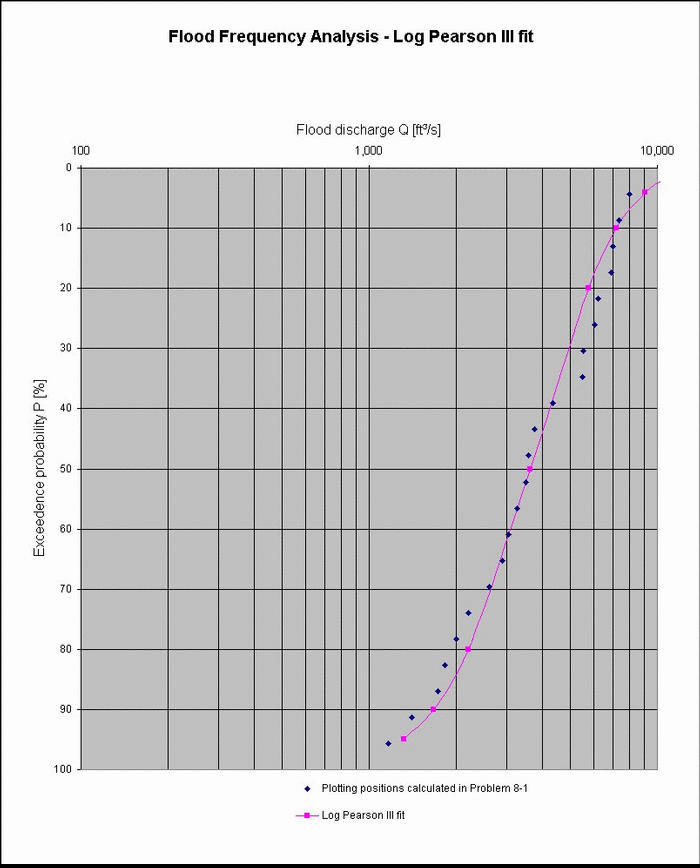
The record length is: n= 22. The values are ranked in descending order, with rank m. Using the Weibull formula, the probability of exceedence (percent) is: P= 100[m/(n+1)]. The return period is: T= (n+1)/m. The calculations are shown in the following table.

Year Annual Flood Ranking Values Rank Probability Return Period
[ft³/s] [ft³/s] (%) (y)
1 8,020 8,020 1 4.35 23.00
2 3,260 7,350 2 8.70 11.50
3 2,210 7,015 3 13.04 7.67
4 1,735 6,925 4 17.39 5.75
5 5,550 6,215 5 21.74 4.60
6 3,560 6,080 6 26.09 3.83
7 3,745 5,550 7 30.43 3.29
8 3,040 5,505 8 34.78 2.88
9 3,500 4,350 9 39.13 2.56
10 2,010 3,745 10 43.48 2.30
11 1,835 3,560 11 47.83 2.09
12 7,350 3,500 12 52.17 1.92
13 4,350 3,260 13 56.52 1.77
14 2,890 3,040 14 60.87 1.64
15 2,620 2,890 15 65.22 1.53
16 1,405 2,620 16 69.57 1.44
17 1,165 2,210 17 73.91 1.35
18 5,505 2,010 18 78.26 1.28
19 6,080 1,835 19 82.61 1.21
20 6,215 1,735 20 86.96 1.15
21 7,015 1,405 21 91.30 1.10
22 6,925 1,165 22 95.65 1.05

Problem 8-2

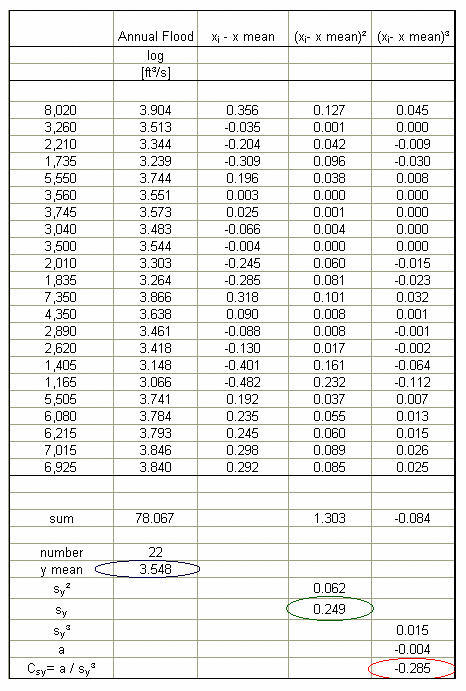
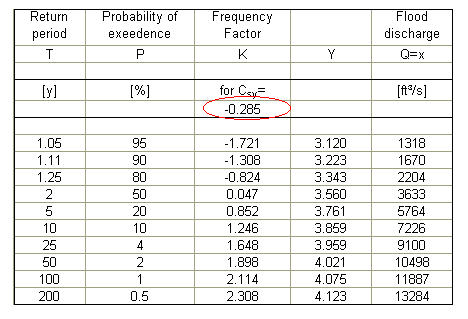
The statistics of the logarithms can be calculated with a spreadsheet. The results are: mean: y(bar)= 3.548; standard deviation: sy= 0.249; skew coefficient: Csy= -0.285


Problem 8-3

(a) For return period T = 100-y, the complementary cumulative probability is: 1/T = 0.01. Therefore, the cumulative probability to the right of the mean is: F(z) = 0.50-0.01 = 0.01. The corresponding standard unit (Table A-5, Appendix A) is: z = 2.327. The 100-y flood is: Q100 = 1550+ (2.327 x 435) = 2562 m3/s ANSWER.
(b) For return period T = 100-y, the Gumbel variate (Eq. 6-39) is: y = 4.6. For record length n = 35, the mean and standard deviation of the Gumbel variate (Table A-8) are 0.5403 and 1.1285, respectively. Therefore, the frequency factor (from Eq. 6-40) is: K = 3.597. The 100-y flood is: Q100 = 1550 + (3.597 x 435) = 3115 m3/s ANSWER.
(c) For return period T = 100-y and skew coefficient of the logarithms -0.2, the frequency factor is obtained from Table A-6 by linear interpolation: K = 2.178. Therefore: y = 3.05+ (2.178 x 0.3) = 3.7034. The 100-y flood is: Q100 = log-1(3.7034) = 5051 m3/s ANSWER.