SPRING 2009
SOLUTION TO HOMEWORK 6, CHAPTER 5
Problem 6-1
Running online curve number: Q = 2.71 in.
Problem 6-2
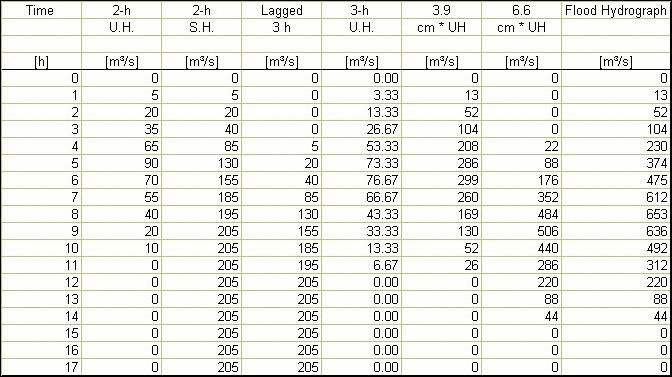
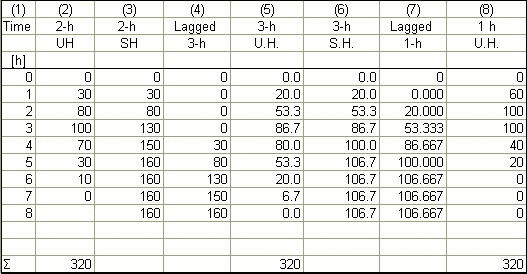
The 3-h unit hydrograph is shown in Col. 5; the 1-h unit hydrograph is shown in Col. 8. The sum of Cols. 2, 5, and 8 is the same.
The output from online S-hydrograph (attached) verifies hand calculations. ANSWER.
Problem 6-3
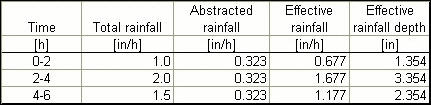
The total rainfall in the 6-h period is: P = 9 in. With runoff curve number CN = 84 and total rainfall P = 9 in., use Eq. 5-8 to calculate the direct runoff Q: Q = 7.06 in. Assume φ-index between 0 and 0.5 in./h. Therefore: [ (1.0 - φ) • 2 h + (2.0 - φ) • 2 h + (1.5 - φ) • 2 h ] = 7.06 in. Solving for φ: φ = 0.323 in/h. Rainfall intensities and depths are as follows.
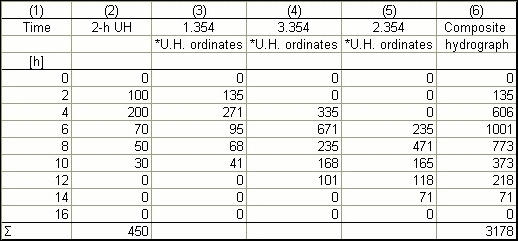
The unit hydrograph is convoluted with the effective rainfall depth pattern as shown in the following table.
To verify that the composite-hydrograph ordinates are correct, the radio of sums ( 3178 / 450 = 7.06) should be equal to the sum of the effective rainfall depth: (1.354 + 3.354 + 2.354) = 7.06. The composite hydrograph for the effective storm pattern is shown in Col. 6.
The output from online Convolution (attached) verifies hand calculations. ANSWER.
To convolute the 2-h unit hydrograph with the effective storm pattern defined at intervals of 3 h, it is necessary to change the unit hydrograph duration to 3 h. The change in unit hydrograph duration and unit hydrograph convolution are shown in the following table. The same results are obtained with online programs S-hydrograph
and Convolution (see attached).
Problem 6-4