CIVE 530 - OPEN-CHANNEL HYDRAULICS
LECTURE 6: COMPUTATION OF UNIFORM FLOW

6.1 CONVEYANCE

The discharge in steady flow is the product of the velocity times the water area.

Q = V A

Q = V A = C A R^x S^y

Q = K S^y

The quantity K is the conveyance of the channel section, a function of friction, area, and wetted perimeter.

K = C A R^x

Under Manning or Chezy:

Q = K S^1/2

and the conveyance is:

K = Q / S^1/2

Under Chezy:

K= C A R^1/2

Under Manning:

K= (1.486/n) A R^2/3

6.1 CHANNEL SECTION WITH COMPOSITE ROUGHNESS

Assume a channel with varying roughness along its wetted perimeter (discrete variation).
Assume the wetted perimeters are P₁, P₂, P₃, ... P_N.
Assume the corresponding roughnesses (Manning n) are n₁, n₂, n₃, ... n_N.
Horton assumed that all subsections have the same velocity, equal to the mean velocity:
V₁ = V₂ = V₃ = V_N = V.

V_i = (1.486/n_i) R_i^2/3S^1/2

V_i = (1.486/n_i) (A_i^2/3/P_i^2/3) S^1/2

A_i = V_i^3/2 n_i^3/2 P_i / (1.486^3/2 S^3/4)

The total area is:

A = V^3/2 n^3/2 P / (1.486^3/2 S^3/4)

The total area is:

A = ∑_N A_i

Therefore:

V^3/2 n^3/2 P = ∑_N V_i^3/2 n_i^3/2 P_i

Since:

V = V_i

Then:

n^3/2 P = ∑_N n_i^3/2 P_i

It follows that the composite value of n is:

n = [∑_N( n_i^3/2P_i) / P ] ^2/3

Channels of Compound Section
A natural channel usually consists of a main channel and two side channels.

Fig. 6-6 (Chow)

Let v₁, v₂, v₃, v_N, be the mean velocities in the subsections.
Let α₁, α₂, α₃, α_N, be the α velocity-distribution coefficients in the corresponding subsections.
Let β₁, β₂, β₃, β_N, be the β velocity-distribution coefficients in the corresponding subsections.
Let ΔA₁, ΔA₂, ΔA₃, ΔA_N, be the water areas in the corresponding subsections.
From continuity:

v₁ = (K₁/ΔA₁) S^1/2

v₂ = (K₂/ΔA₂) S^1/2

v₃ = (K₃/ΔA₃) S^1/2

v_N = (K_N/ΔA_N) S^1/2

Q = V A = v₁ ΔA₁ + v₂ ΔA₂ + v₃ ΔA₃ + ... + v_N ΔA_N

Q = V A = (K₁ + K₂ + K₃ + ... K_N) S^1/2

Q = V A = (Σ K_N) S^1/2

Therefore, the mean velocity of the total section is:

V = (Σ K_N) S^1/2 / A

The velocity-distribution coefficients are:

α = ∑ v³ ΔA / (V³ A)

β = ∑ v² ΔA / (V² A)

Incorporating the velocity into the definitions of velocity-distribution coefficients, the composite values of α and β are, respectively:

α = [ Σ (α_N K_N³ / ΔA_N²) ] / [(Σ K_N)³ / A² ]

β = [ Σ (β_N K_N² / ΔA_N) ] / [(Σ K_N)² / A ]

6.6 DETERMINATION OF NORMAL DEPTH AND VELOCITY

The normal depth and velocity can be computed using the Manning equation.

Fig. 2-2 (Chow)

Example 6-2. Compute the normal depth and velocity of the trapezoidal channel shown above, carrying 400 cfs, with b = 20 ft, z = 2, S_o = 0.0016, and n = 0.025.
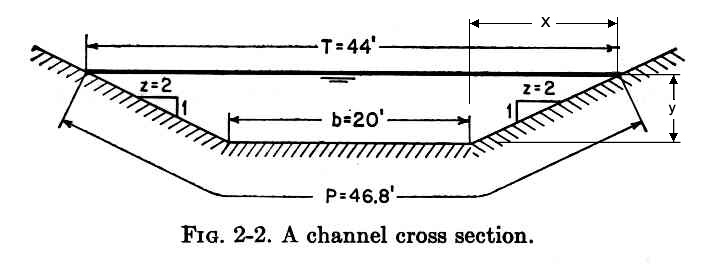
Solution.- The following proportion holds:     z/1 = x/y
From which:    x = zy
T = b + 2x = b + 2zy
A= (1/2) (b + T) y = (1/2) (b + b + 2zy) y = (b + zy) y
P = b + 2 (y² + z²y²) ^1/2 = b + 2y (1 + z²)^1/2
R = { [(b/2) + (zy)/2] y}    / [ (b/2) + y (1 + z²)^1/2 ]
Q = (1.486/n) A R^2/3 S^1/2
(Qn) / (1.486 S^1/2) = A R^2/3

(Qn) / (1.486 S^1/2) = {2[(b/2) + (zy)/2] y}    {[(b/2) + (zy)/2]y }   ^2/3 / [ (b/2) + y (1 + z²)^1/2 ]^2/3

[(Qn) / (1.486 S^1/2)] [ (b/2) + y (1 + z²)^1/2 ]^2/3 = 2 {[(b/2) + (zy)/2] y }    ^5/3

[(Qn) / (2 × 1.486 S^1/2)] [ (b/2) + y (1 + z²)^1/2 ]^2/3 = {[(b/2) + (zy)/2] y }    ^5/3

[(Qn) / (2 × 1.486 S^1/2)]^3/2 [ (b/2) + y (1 + z²)^1/2 ] = {[(b/2) + (zy)/2] y}    ^5/2

{ [(b/2) + (zy)/2] y}   ^5/2 - { [(Qn) / (2 × 1.486 S^1/2)]^3/2 [(1 + z²)^1/2]y}   - [(Qn) / (2 × 1.486 S^1/2)]^3/2 (b/2) = 0
[(Qn) / (2 × 1.486 S^1/2)]^3/2 = 771.5
(1 + z²)^1/2 = 2.236
{ [(b/2) + (zy)/2] y}    ^5/2 - [(771.5 × 2.236)y] - 771.5 (b/2) = 0
[(10 + y)y]^5/2 - 1725y - 7715 = 0
By trial and error:
y_n = 3.36 ft.
A_n = [(b + zy_n) y_n] = 89.78 ft.
V_n = Q/A_n = 400/89.78 = 4.46 fps.

The normal flow depth equation is:

f(y) = { [(b/2) + (zy)/2] y }   ^5/2 - { [(Qn) / (2 × 1.486 S^1/2)]^3/2 [(1 + z²)^1/2]y}   - [(Qn) / (2 × 1.486 S^1/2)]^3/2 (b/2) = 0

f(y) = { [(b/2) + (zy)/2] y }   ^5/2 - { [(Qn) / (2.972 S^1/2)]^3/2 [(1 + z²)^1/2]y}   - [(Qn) / (2.972 S^1/2)]^3/2 (b/2) = 0
Changing variable to x for simplicity:
f(x) = { [(b/2) + (zx)/2] x }   ^5/2 - { [(Qn) / (2.972 S^1/2)]^3/2 [(1 + z²)^1/2]x}   - [(Qn) / (2.972 S^1/2)]^3/2 (b/2) = 0

To solve this equation by trial and error (brute force method), the following simple algorithm is suggested:

Assume x = 0.
Assume Δx = 1.
Increment x:    x_o = x + Δx
Calculate f(x_o)
Stop when Δx is small enough (calculate output variables).
If f(x_o) < 0, return to step 3
If f(x_o) > 0, set Δx = 0.1 Δx
Set x_o = x_o - 9 Δx and return to step 4

Solution by using Newton's approximation:

f(x) = { [(b/2) + (zx)/2] x}   ^5/2 - { [(Qn) / (2.972 S^1/2)]^3/2 [(1 + z²)^1/2]x}   - [(Qn) / (2.972 S^1/2)]^3/2 (b/2)

f'(x) = x^5/2 (5/2) [(b/2) + (zx)/2] ^3/2 (z/2) + [(b/2) + (zx)/2] ^5/2 (5/2) x^3/2 - [(Qn) / (2.972 S^1/2)]^3/2 (1 + z²)^1/2
f'(x) = (5/4) zx^5/2 [(b/2) + (zx)/2]^3/2 + (5/2) x^3/2 [(b/2) + (zx)/2]^5/2 - [(Qn) / (2.972 S^1/2)]^3/2 (1 + z²)^1/2

[When the root x_r is approached from the left (x_o < x_r), the slope f'(x_o) is positive, f(x_o) is negative, and the denominator (x_o - x_r) is negative].

[When the root x_r is approached from the right (x_o > x_r) (the usual case), the slope f'(x_o) is positive, f(x_o) is positive, and the denominator (x_o - x_r) is positive].

Newton's iteration with the root approached from the right.

Thus:
f'(x_o) = f(x_o) / (x_o - x_r)

The root is:
x_r = x_o - f(x_o) / f'(x_o)

To solve the normal flow depth equation using Newton's approximation, the following algorithm is suggested:

Assume x = 0.
Assume Δx = 1.
Increment x:    x_o = x + Δx
Calculate f(x_o)
If f(x_o) < 0, return to step 3
If f(x_o) > 0, then:
Calculate the root:
x_r = x_o - [f(x_o) / f'(x_o)]
Stop when x_r - x_o is small enough (calculate output variables).
Otherwise, set x_o = x_r and return to step 7.

6.7 THEORY OF THE MANNING EQUATION

In 1891, the Frenchman Flamant attributed to Manning that Chezy C was a function of hydraulic radius:

C = (1/n) R^1/6

v = C R^1/2 S^1/2 = (1/n) R^2/3 S^1/2
Metric

In U.S. customary units (1 m = 3.28 ft):

v/3.28 = (1/n) (R/3.28)^2/3 S^1/2
U.S. customary units

v = (3.28)^1/3 (1/n) R^2/3 S^1/2
U.S. customary units

v = (1.486/n) R^2/3 S^1/2
U.S. customary units

Williamson plotted in 1951 the Darcy-Weisbach friction factor vs relative roughness:

f_D = 8g/C² = 0.113 (R/k_s)^-1/3

where k_s is the linear measure of roughness (grain size).
Replacing k_s for d₈₄ (diameter for which 84% is finer) and solving for C:

C = (8g/0.113)^1/2 (R/d₈₄)^1/6

C = 1.486 R^1/6 / (0.031 d₈₄^1/6)

Therefore:

n = 0.031 d₈₄^1/6
U.S. customary units

The general formula for Manning's n as a function of relative roughness R/k and absolute roughness k is:

n = f (R/k) k^1/6

Strickler used a constant for f (R/k) = 0.0342, and the median grain size (d₅₀) as the absolute roughness:

n = 0.0342 d₅₀^1/6
U.S. customary units

For d₅₀ = 10 ft:    n = 0.050
For d₅₀ = 1 ft:    n = 0.034
For d₅₀ = 0.1 ft:    n = 0.023
For d₅₀ = 0.01 ft:    n = 0.016
For d₅₀ = 0.001 ft:    n = 0.011
For d₅₀ = 0.0001 ft:    n = 0.007
The actual minimum value of n = 0.008 (lucite surface) (Chow).

6.9 COMPUTATION OF FLOOD DISCHARGE: THE SLOPE-AREA METHOD

The slope-area method is used to calculate flood discharges when field data regarding wetted cross sections and energy slopes is available.
The steps in the application of the slope-area method are the following:

With known upstream and downstream flow areas and hydraulic radius, and average value of Manning n for the reach, compute the conveyances:

K_u = (1.486/n) A_u R_u^2/3

K_d = (1.486/n) A_d R_d^2/3

Compute the average conveyance for the reach (the geometric mean):

K = (K_uK_d)^1/2

Assuming zero velocity-head difference, the first approximation to the energy slope is equal to the fall of water surface elevation divided by the reach length:

S_e = F / L

The first approximation of the discharge is:

Q = K S_e^1/2

Compute the velocity heads upstream and downstream:

h_u = α_u V_u²/(2g) = α_u (Q/A_u)²/(2g)

h_d = α_d V_d²/(2g)= α_d (Q/A_d)²/(2g)

The new energy slope is:

S_e = h_f / L = [F + k(h_u - h_d)] / L

where k = 1 if the reach is contracting (V_u < V_d), and k = 0.5 is the reach is expanding (V_u > V_d),. The reduction in k accounts for the recovery of the flow during expansion.
The new discharge is:

Q = K S_e^1/2

Go back to step 5 and repeat steps 5-7 until the calculated discharge (new discharge) has converged to a constant value (usually 3-4 iterations).

Example.

Local man showing water level reached by flood, Kanakumbe, Karnataka, India, December 1991.

6.10 UNIFORM SURFACE FLOW

Overland flow over a surface can be described as uniform surface flow.
This type of flow is also referred to as sheet flow, when the depth is small compared to the width.
The flow may be laminar or turbulent.
If the flow depth is small, viscosity dominates and the flow is laminar.

Fig. 6-9 (Chow)

The acting shear stress is:

τ = γ (y_m - y) S

According to Newton's law of viscosity, the resisting shear stress is:

τ = μ (dv/dy)

Therefore:

μ (dv/dy) = γ (y_m - y) S

dv = (γ/μ) (y_m - y) S dy

But:

γ = ρg

μ = ρν

Then:

dv = (gS/ν) (y_m - y) dy

Integrating:

v = ∫ dv = ∫ (gS/ν) (y_m - y) dy

v = (gS/ν) [ (y_my) - (y²/2) ] + C

For v = 0: y = 0. Then C = 0.
The velocity-depth function is:

v = (gS/ν) [ (y_my) - (y²/2) ]

Thus, the velocity of uniform sheet flow has a parabolic distribution.
Integrate the velocity distribution to find the rating:

q = ∫ vdy = (gS/ν) ∫ [ (y_my) - (y²/2) ] dy
(Between the limits of 0 and y_m)

q = (gS/ν) [ (y_m³/2) - (y_m³/6) ]
(Between the limits of 0 and y_m)

q = (gS/ν) [ (1/3)y_m³ ]

q = [ (gS)/(3ν) ] y_m³ = C_L y_m³

C_L = (gS)/(3ν)

Note that in laminar flow the exponent of the rating is 3, and the rating is a function of the internal friction ν
The mean velocity is:

v = q/y_m = [(gS)/(3ν)] y_m² = C_L y_m²

The turbulent flow rating for sheet flow (Manning friction) is:

q = v y_m = (1.486/n) S^1/2 y_m^5/3

Note that in turbulent flow (Manning) the exponent of the rating is 5/3.
The turbulent flow rating for sheet flow (Chezy friction) is:

q = v y_m = C S^1/2 y_m^3/2

Note that in turbulent flow (Chezy) the exponent of the rating is 3/2.
Note that for sheet flow, the exponent of the rating varies between 3/2-5/3 (turbulent) and 3 (laminar).
A value of 2 is mixed laminar-turbulent.
The Vedernikov number is:

V = (β - 1)U/(gD)^1/2

where β is the exponent of the rating and U is the mean velocity.
For β = 3 (laminar):

V = 2U/(gD)^1/2 = 2 F

It follows that in laminar flow, the flow is unstable (V = 1) when F = 0.5.
For β = 3/2 (Chezy turbulent):

V = (1/2)U/(gD)^1/2 = (1/2) F

In turbulent Chezy flow, the flow is unstable (V = 1) when F = 2.
For β = 5/3 (Manning turbulent):

V = (2/3)U/(gD)^1/2 = (2/3) F

In turbulent Manning flow, the flow is unstable (V = 1) when F = 3/2.

140404