Name: ______________________ Red ID __________________ Grade: _________

1. (25%) A planned reservoir has a total capacity of 5 million cubic meters (5 hm³). The catchment drainage area is 200 km². The mean annual runoff in the basin is 500 mm. The sediment yield is 1,350 Metric tons/km²/yr. The specific weight of sediment deposits is estimated at 13,000 N/m³. The sediments are coarse grained. How long will it take the reservoir to fill up to 80% capacity? Use five increments of reservoir capacity.

   ---

   The mean annual water inflow is:

   I = 500 mm × 200 km²

   I = 500 mm × 200 km² × 100 hm²/km² × 0.001 m/mm × 0.01 hm/m

   I = 100 hm³

   The annual sediment inflow is:

   I_s =

   1350 M.tons/km²/yr × 1000 kg/M.tons × 200 km² × 9.81 N/kg / (13000 N/m³ × 1000000 m³/hm³)

   I_s = 0.204 hm³/yr

   Interval	Reservoir capacity (hm3)	Accumulated volume (hm3)	C/I ratio	Average C/I in interval	Trap efficiency (%)	Number of years to fill	Cumulative number of years to fill
   0	5	0	0.05	-	-	-	-
   1	4	1	0.04	0.045	83	5.9	5.9
   2	3	2	0.03	0.035	80	6.1	12.0
   3	2	3	0.02	0.025	75	6.5	18.5
   4	1	4	0.01	0.015	64	7.7	26.2

   ---

2. (20%) Calculate the diameter of a concrete culvert to pass the 50-yr flood, with Q₅₀ = 265 cfs. The inlet invert elevation is z₁ = 180 ft. The natural streambed slope is S_o = 0.01. The tailwater depth above the outlet invert is y₂ = 4.2 ft. The culvert length is 250 ft. The roadway shoulder elevation is 196 ft. Assume a 2-ft freeboard. Assume a circular concrete culvert (f = 0.018, n = 0.012), and square edge with headwalls.

   ---

   THE DESIGN ELEVATION FOR U/S POOL IS:   196 - 2 = 194 FT.

   FIRST ASSUME OUTLET CONTROL.

   ASSUME THAT THE HGL IS AT THE ELEVATION OF THE D/S POOL.

   CALCULATE OUTLET INVERT ELEVATION:   z₂ = 180 - (0.01 × 250) = 180 - 2.5 = 177.5 FT.

   CALCULATE D/S POOL ELEVATION:   177.5 + 4.2 = 181.7 FT.

   SET UP ENERGY EQUATION:   z₁ + y₁ + V₁²/(2g) = z₂ + y₂ + V₂²/(2g) + ∑h_L

   ASSUME V₁ = 0   [VELOCITY IS ZERO IN THE U/S POOL]

   ASSUME V₂ = 0   [VELOCITY DISSIPATES TO ZERO IN THE D/S POOL]

   ∑h_L = [K_e + K_E + f(L/D)] V²/(2g)

   ASSUME K_e = 0.5; K_E = 1.   [TABLE 5-3]

   ASSUME f = 0.018

   ENERGY EQUATION:   194 = 181.7 + [0.5 + 1.0 + 0.018 (250/D)] V²/(2g)

   12.3 = [1.5 + 4.5/D] V²/(2g)

   V = Q/A = 265/A = 265/[(π/4)D²]

   V²/(2g) = { 265²/[(π/4)²D⁴] }   / (2g)

   12.3 = 265² [1.5 + 4.5/D] / [(π/4)²D⁴ (2 × 32.17)]

   SOLVE BY TRIAL AND ERROR:   D = 4.3 FT.

   CHOOSE NEXT LARGER SIZE:   D = 4.5 FT.

   WITH Q = 265, AND D = 4.5 FT = 54 IN, ENTER FIG. 7-5 TO FIND RATIO HEADWATER DEPTH OVER DEPTH HW/D = 3.0
   

   
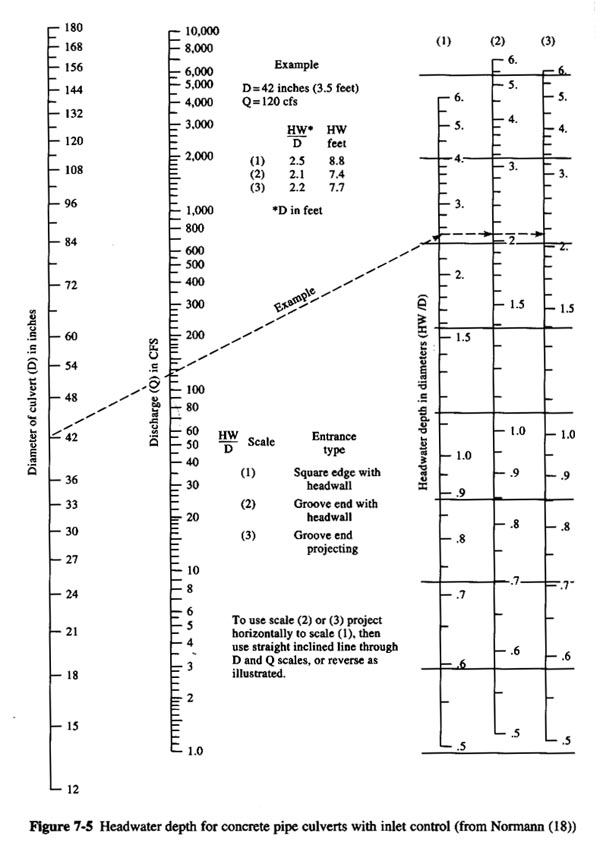
   HW DEPTH = 3.0 × 4.5 = 13.5 FT.

   U/S POOL ELEVATION = 180 + 13.5 = 193.5   SMALLER THAN 194.   OK.

   CHECK CRITICAL DEPTH.

   COMPUTE THE SECTION FACTOR:   Q/(g^1/2d_o^5/2) = 265 / [32.17)^1/2(4.5)^5/2] = 1.09

   ENTER FIG. 4-15, WITH SECTION FACTOR 1.09:   y_c/d_o = 0.95

   
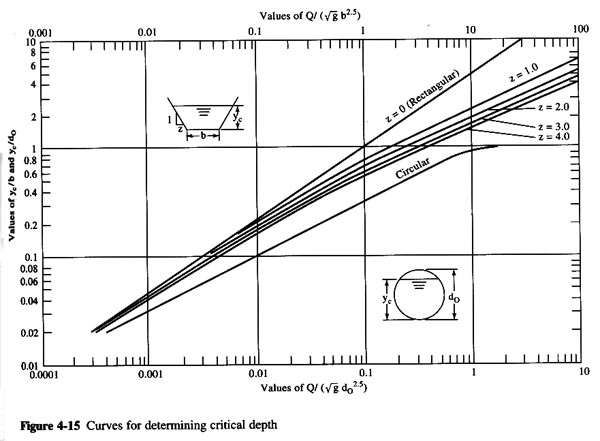
   THUS: y_c = 4.28 FT.     ANSWER.

   CHECK NORMAL DEPTH.

   ASSUME n = 0.013.

   COMPUTE THE SECTION FACTOR:   Qn/(1.486 × S_o^1/2 × d_o^8/3 ) = 265 × 0.012 / (1.486 × 0.01^1/2 × 4.5^8/3) = 0.38

   ENTER FIG. 4-7, WITH SECTION FACTOR 0.38:   y_n/d_o = 0.8

   
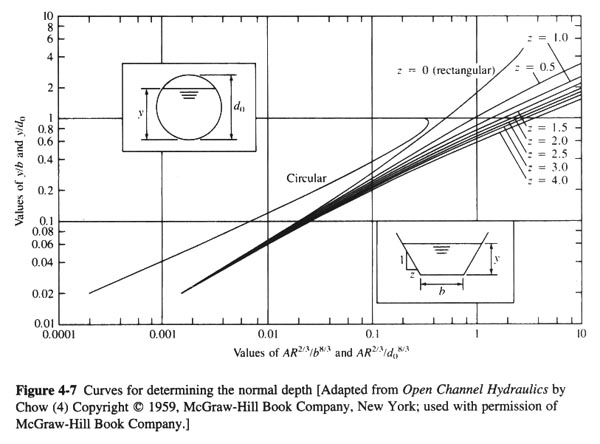
   THUS: y_n = 3.6 FT.     ANSWER.

   BECAUSE y_n < y_c, THE FLOW IS SUPERCRITICAL.

   BECAUSE TW < y_c, THERE WILL BE NO HYDRAULIC JUMP NEAR THE OUTLET.

   BECAUSE THE FLOW IS SUPERCRITICAL IN THE PIPE AND THE OUTLET IS OPEN TO THE ATMOSPHERE (TW DEPTH < D) WE CAN CONCLUDE THAT THERE IS INLET CONTROL.

   DESIGN DIAMETER:   D = 4.5 FT = 54 IN.    ANSWER.

   ---

3. (20%) Given V_o = 8 fps and V_A = 12 fps at p_o = 20 psia, calculate the pressure coefficient C_p and the velocity V_o that will just begin to cause cavitation in the slot. Assume T = 70^oF.

   ---

   V_A = V_o(1 - C_p)^1/2

   C_p = 1 - (V_A²/V_o²)

   C_p = 1 - (12²/8²) = -1.25    ANSWER.

   σ_{i B} = 1 - 2 C_p = 1 - 2 (-1.25) = 3.5

   σ_{i B} = (p_o - p_v) / (ρV_o² /2)

   T= 70^oF:     p_v = 0.363 psia

   3.5 = (20 × 144 in²/ft² - 0.363 × 144 in²/ft²) / (ρ V_o² /2)

   3.5 = (2880 - 52.27) / (1.94 V_o² /2)

   V_o = 28.86 fps.     ANSWER.

   ---

4. (20%) Given the system shown below, what is the discharge Q (m³/s) and corresponding head H (m) at the system operating point? Assume sharp entrance and exit losses. Assume f = 0.018. The performance curve of the pump is given by: H = 60 - 600 Q²

   ---

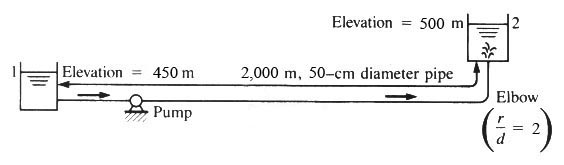
   h_p = (z₂ - z₁) + [V²/(2g)] [f (L/D) + ∑ K_L ]

   h_p = (z₂ - z₁) + [ Q²/(2gA²)]  [ f (L/D) + K_e + K_b + K_E ]

   From Table 5-3 (in the text):   K_e = 0.5; K_b = 0.19; K_E = 1

   h_p = (500 - 450) + [ Q²/(2g ((π/4) D²)²) ] [ 0.018 (2000/0.5) + 0.5 + 0.19 + 1 ]

   h_p = 50 + [ Q²/(2 (9.81) ((π/4)² (0.5)⁴)) ] (73.69)

   h_p = 50 + [ Q²/(0.7564) ] (73.69)

   h_p = 50 + 97.42 Q²

   Pump performance curve:   H = 60 - 600 Q ²

   At H = h_p:   Q = 0.1197 m³/s    ANSWER.

   h_p = 50 + 97.42 (0.1197) ² = 51.395 m.    ANSWER.

   ---

5. (20%) What head ΔH (m) will be developed for an axial-flow pump of D = 0.3 m operating at n = 900 rpm and discharging Q = 100 L/s? What power P (KW) will be required? The pump dimensionless performance curves are shown below.

   ---

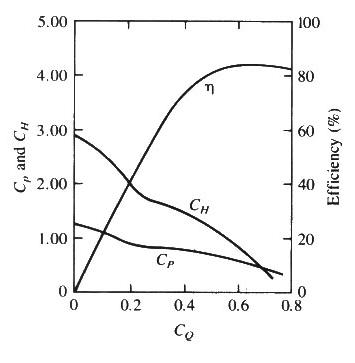
   Q = 100 L/s = 0.1 m³/s

   n = 900 rpm = 900 rpm / 60 s/m = 15 rps

   C_Q = Q/(nD³) = 0.1 /(15 × 0.3³) = 0.247

   C_H = 1.78

   C_P = 0.81

   C_H= ΔH / (D² n² / g)

   ΔH = C_H D² n² / g = 1.78 × 0.3² × 15² / 9.81

   ΔH = 3.67 m     ANSWER.

   C_P = P / (ρ D⁵ n³)

   P = C_P ρ D⁵ n³

   P = 0.81 × 1 × 0.3⁵ × 15³

   P = 6.64 KN m/s

   P = 6.64 KW     ANSWER.

   ---