1. INTRODUCTION
The kinematic and diffusion wave models have found wide application in
engineering practice. Both are approximations to the unsteady open channel
flow phenomenon described by the complete Saint Venant equations. The
diffusion model assumes that the inertia terms in the equation of motion are
negligible as compared with the pressure, friction, and gravity terms. The
kinematic model assumes that inertia and pressure terms are negligible as
compared with the friction and gravity terms.
2. WAVE PROPAGATION IN OPEN CHANNEL FLOW
Recently, two of the writers (4) have developed an analytical solution for
wave propagation in open channel flow, based on a linearized form of the
Saint Venant equations as presented by Lighthill and Whitham (3). They took
the linearized equations and sought a solution in sinusoidal form which led
to a system of homogeneous linear equations.
3. DEFINITIONS
The following definitions are advanced: uo = steady uniform flow mean velocity;
do = steady uniform flow depth; So = bed slope; L = wavelength of sinusoidal
perturbation to steady equilibrium flow; T = wave period of sinusoidal perturbation
to steady equilibrium flow; c = wave celerity; Lo = reference channel
length; Fo = steady uniform flow Foude number; σ*= dimensionless wave number
of the unsteady component of the motion; and τ* = dimensionless wave period
of the unsteady component of the motion, such that
in which g = the acceleration of gravity.
The propagation celerity c can be expressed in dimensionless form by dividing it by uo. The dimensionless propagation celerity c* is
The logarithmic decrement δ (5) is defined as
in which αo and α1 = the wave amplitudes at the beginning and end of one wave period, respectively.
Two of the writers (4) have shown that for the dynamic model (that based
on the complete Saint Venant equations), the dimensionless propagation celerity
c and logarithmic decrement δ are functions of Fo and σ* (see Appendix I).
In practice, however, it is desirable to express the space parameter σ* as a function of the time parameter τ*. Combining Eqs. 1, 4, 5, and 6
Thus, c* and δ can be expressed as a function of Fo and τ* by use of Eq. 8.
Furthermore, the results of the theory suggest that for the comparison of diffusion and full dynamic models,
a more appropriate parameter is τ*/Fo. Making use of Eqs. 2, 3 and 5, τ*/Fo is expressed as
or
4. KINEMATIC WAVE VERSUS DIFFUSION WAVE
The kinematic model breaks down when the neglect of the pressure term
is not justified. Accordingly, it is of interest to compare the kinematic and
diffusion models. Both models have a propagation celerity equal to 1.5 times
the equilibrium flow velocity. They differ, however, in the attenuation. The
logarithmic decrement of the kinematic model is 0, i.e., the kinematic model
does not allow for physical attenuation. The attenuation often observed in
numerical schemes based on the kinematic model is of an artificial nature
(numerical damping due to truncation errors) (1). The logarithmic decrement
of the diffusion model is (4)
If water discharge and channel friction are given, uo and do can be calculated
by the use of the appropriate uniform flow formula (Manning or Chezy).
An explanatory note is necessary here. The criteria of Table 1 are based on a comparison of the attenuation
(described by the logarithmic decrement δ) of the analytical solutions for the kinematic and diffusion models.
In a numerical solution, however, often the truncation errors may mask the nondiffusive character of the analytical
solution of the kinematic wave, with the result that the numerical solution of the kinematic wave may resemble the
analytical solution of the diffusion wave (1), further complicating the modeling.
5. DIFFUSION WAVE VERSUS DYNAMIC WAVE
The next step in the analysis is to compare the propagation celerity c*d
and logarithmic decrement δd of the diffusion model with those of the full dynamic model. For Fo < 2,
the propagation celerity of the diffusion wave, c*d = 1.5,
is a lower bound for the dynamic celerity. Since only the primary dynamic wave (that which travels downstream) is of interest here, the dynamic wave
celerity will be referred to as c*1.
6. FULL DYNAMIC MODEL
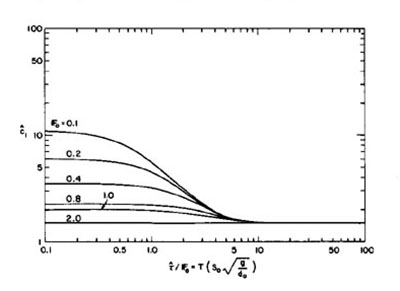
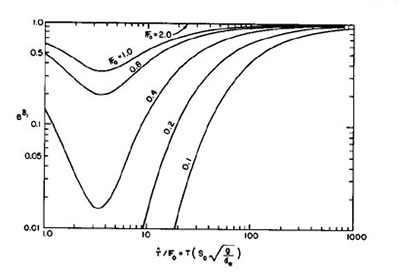
Figures 1 and 4 show c*1 and eδ1 as a function of Fo
and τ*/Fo, respectively. For τ*/Fo
≤ 30, i.e., the range where only the full dynamic model would apply,
very strong attenuation is shown. For instance, for
7. CONCLUSIONS The applicability of the kinematic and diffusion models is assessed by comparing the propagation characteristics of sinusoidal perturbations to the steady uniform flow for the kinematic, diffusion, and dynamic models (the dynamic model is that based on the complete Saint Venant equations). The comparison allows the determination of inequality criteria that need to be satisfied if the kinematic or diffusion models are to simulate the physical phenomena within a prescribed accuracy.
ACKNOWLEDGEMENTS The writers wish to acknowledge the United States Environmental Protection Agency, Environmental Research Laboratory, Athens, Georgia, and the United States Department of Agriculture Forest Service, Rocky Mountain Forest and Range Experiment Station, Flagstaff, Arizona, for sponsoring this study.
APPENDIX I. - EQUATIONS FOR PROPAGATION CELERITY c* AND LOGARITHMIC DECREMENT δ The equations for c* and δ of the complete dynamic model are
in which A = (1/Fo2) - B 2; B = 1/(σ*Fo2); C = (A 2 + B 2)1/2; D = [(C + A)/ 2]1/2; and
APPENDIX II. - REFERENCES
APPENDIX III.- NOTATION The following symbols are used in this paper:
αo = wave amplitude at beginning of period; α1 = wave amplitude at end of period; c = wave celerity. Eq. 1; c* = dimensionless wave celerity, Eq. 6; do = steady uniform flow depth; δ = logarithmic decrement, Eq. 7; τ* = dimensionless period, Eq. 5; and σ* = dimensionless wave number, Eq. 4.
Subscripts 1 = pertaining to primary dynamic wave (traveling downstream); d = pertaining to diffusion model; and k = pertaining to kinematic model.
| ||||||||||||||||||||||||||||||||||||||||||||||
| 150610 23:10 |
| Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader. |