♦ This page can be better viewed with Mozilla Firefox ♦
|
Fig. 1 Headwaters of the La Leche basin, near Incahuasi.
|
LA LECHE RIVER FLOOD CONTROL PROJECTLAMBAYEQUE, PERU
SECOND PROJECT REPORT PRELIMINARY FINDINGS
APRIL 30, 2008
Dr. Victor M. Ponce
Hydrology Consultant
1. INTRODUCTION
D'Leon Consulting Engineers, of Long Beach, California, hereafter referred to as DLCE,
has a contract with the Regional Government of Lambayeque, Peru, hereafter RGL,
to support the development of the La Leche River flood control project.
The study aims to enhance flood control and water conservation in the watershed of the La Leche river, which has
suffered major floods caused by the El Niño phenomenon.
The funding agency is the U.S. Trade and Development Agency (UST&DA).
The local government agency in charge of the project is the Proyecto Especial Olmos-Tinajones, hereafter PEOT.
Dr. Victor M. Ponce, hereafter the Consultant or VMP, has a subcontract with DLCE
to perform the hydrologic component of the study.
This second report is submitted in partial fulfillment of the requirements of the contract between VMP and DLCE.
The report contains a description of the progress to date and a summary of preliminary findings.
2. PROJECT DESCRIPTION
The project encompasses the feasibility design of the structure [or structures] to control floods and store flood waters [for future use] in the La Leche river.
Two damsites are currently being considered: (1) La Calzada, and (2) Calicantro (DEPOLTI, 1998). While La Calzada is an instream dam, Calicantro is an off-stream dam.
The comparison between these alternatives is given in Table 1.
| Table 1.
Comparison between damsite alternatives.
|
| Capability
| Damsite alternative
| La Calzada
| Calicantro
| La Calzada plus Calicantro
|
| Flood control
| Very good
| Poor
| Very good
|
| Water storage
| Fair
| Very good
| Very good
|
| Service life
| Short
| Long
| Long
|
|
|
A dam only at La Calzada would go a long way to store the floods. However, in order to be effective for this purpose,
most of the active storage would have to be retarding-pool storage. Therefore, a dam only at La Calzada cannot effectively serve the purpose
of storage of flood waters for later use. In addition, a large instream reservoir such as that of La Calzada would have a tendency to
store great quantities of sediment, decreasing the service life of the structure (preliminary estimates indicate that it may be less than
100 years).
A dam only at Calicantro would store great quantities of water for later use. However, it could not serve the purpose of effectively
attenuating infrequent La Leche floods.
Therefore, a dam only at Calicantro will not solve the flood hazard in the La Leche river. A Calicantro dam
would not be subject to deposition of great quantities of sediment, increasing the service life, provided the proper
exclusion works are in place and are operated effectively.
The solution is to build two dams, one at La Calzada, primarily for flood control, and another at Calicantro, primarily to store water for
irrigation and other uses. An added feature of the two-dam strategy is that the useful life of the reservoirs, particularly the one at La Calzada,
will be increased. The water will never stay too long in La Calzada, and it could be desilted prior to sending it to Calicantro for storage.
The dam at La Calzada requires a thorough appraisal of the flood hydrology, since it is a major dam located upstream of significant population centers and
important infrastructure.
The dam at Calicantro has a comparatively large volume and small drainage area; therefore, regional floods should not be a problem, assuring
the safety of the dam against overtopping. The spillway would still need to be designed, and its capacity calculated.
The approach is to model the event rainfall-runoff process in the entire La Leche basin, from headwaters to La Calzada.
This will allow the calculation of flood hydrographs
to determine the capacity of principal and emergency spillways, and the [minimum] elevation of the dam crest (freeboard).
The principal spillway (PSH), emergency spillway (ESH), and freeboard hydrograph (FBH) will be determined for La Calzada.
Appropriate design hydrographs for Calicantro would also be determined.
3. BASIN DESCRIPTION
The basin of the La Leche river, from headwaters to La Calzada, has a drainage area of 907.36 km2.
The basin is located in the western slopes of the Peruvian Andes.
The largest town within the basin is Incahuasi, with close to 15,000 inhabitants, including the neighboring hamlets.
The distance from Chiclayo, the closest major population center, to Incahuasi is about 180 km.
The time of travel along a winding unpaved road is about 6 hours. Seasonal rainfall can make travel to and from Incahuasi
hazardous and subject to delays.
The headwaters of the La Leche basin are at Cerro Choicopico, at an elevation of 4,230 m above mean sea level.
The La Leche river has two major tributaries,
the Moyan and Sangana rivers.
The hydraulic length of the La Leche river [to La Calzada] along the Moyan tributary, is 44,397 m.
The hydraulic length of the La Leche river along the Sangana tributary is 44,591 m.
Channel slopes vary from as steep as 24% in Quebrada Cascabamba, to 1% near La Calzada.
Mean velocities during flood events vary between 3 and 4 m/s.
The time of concentration during flood events varies from 3 to 4 hr.
The basin has a mixed land use of native forests and shrub, and agriculture on steep slopes, including grazing.
There are significant areas featuring exposed rock and areas with very little soil, which discourages infiltration (Fig. 2).
Average terrain slopes range from 20% to 50%, encouraging surface runoff. Rainfall varies spatially within
the basin; storms are more intense below elevations of 2000 m (toward the west) and less intense above 2000 m (toward the east).
The climate is semiarid toward the west (near the coast), grading to subhumid toward the east (highlands).
 |
|
Fig. 2 Agriculture on steep slopes of La Leche river basin. |
There are three climatological stations within the basin's perimeter: (1) Puchaca, (2) Tocmoche, and (3) Incahuasi.
The Puchaca station is at elevation 300 m; the Tocmoche station is at elevation 1250 m; the Incahuasi station is at elevation 3600 m.
The wettest month in Puchaca is December; on the other hand, the wettest month in Tocmoche and Incahuasi is March.
Puchaca has less annual rainfall but stronger storm intensities.
Incahuasi has more annual rainfall but milder storm intensities.
Tocmoche has annual rainfall and storm intensities intermediate between those of Puchaca and Incahuasi.
| Table 2.
Comparison between climatological stations in the La Leche basin.
|
| Feature
| Station
| Puchaca
| Tocmoche
| Incahuasi
|
| Location
| near La Calzada
| mid-basin
| headwaters
|
| Elevation [a.m.s.l.] (m)
| 355
| 1,450
| 3,078
|
| Wettest month
| December
| March
| March
|
| Annual rainfall
| Low
| Medium
| High
|
| Storm intensity
| High
| Medium
| Low
|
|
|
The storm record has been compiled from 1963 to 1998 (36 years). [Efforts are currently underway to obtain the remainder of the storm record,
from 1999 to 2007 (9 years)].
The maximum recorded 24-hr storm in Puchaca is 150.2 mm; in Tocmoche it is 100.4 mm; in Incahuasi, 81.0 mm. Thus,
storms are of greater intense in the vicinity of Puchaca and less intense near Incahuasi, with Tocmoche lying somewhere in the middle.
4. MODELING STRATEGY
There is a need to determine flood discharges from 100-yr to 10,000-yr return periods.
The only streamgaging station, at Puchaca, has records going back to 1956 (52 years) (Fig. 3).
The maximum flood discharge recorded at Puchaca is 579.75 m3/s.
Geomorphological evidence suggests that long-term flood discharges at La Calzada may have exceeded this value.
The great alluvial plains of the La Leche river could not have been formed without the occurrence of great floods.
 |
|
Fig. 3 Gaging station, Rio La Leche at Puchaca. |
For design purposes, when the required return period (in this case, 10,000 years) greatly exceeds the record length (52 years),
it is recommended that the analysis shift to flood determinations based on rainfall-runoff modeling.
The latter is preferred because it provides
increased flexibility to examine "what if" situations, both with regard to storm patterns (amounts and intensity) and existing/future
soil/cover complexes, while making better use of existing computational resources.
In the case of the La Leche basin, maximum design flood discharges are expected under a suitable combination of the following conditions:
- Rainfall depth: An El Niño event, with large amounts of precipitation, likely to recur every 12 to 15 years, on the average;
- Rainfall coverage: A general storm, covering the entire drainage area;
and
- Rainfall sequence: A major storm following in the heels of another storm, resulting in wet antecedent moisture.
The chosen strategy is to model the flood discharges
of the La Leche basin using the deterministic/conceptual rainfall-runoff model RAINFLO©.
Event precipitation for 100-yr and 10,000-yr return periods will be determined using the statistical techniques
of Log Pearson III and Gumbel. These events will be input to the model to calculate flood discharges for the chosen return periods
and associated design criteria.
5. MODEL DESCRIPTION
RAINFLO© is
a deterministic/conceptual, distributed, event-driven, rainfall-runoff computational model developed
for specific application to flood flows (Ponce et al., 1985).
The model calculates peak flood hydrographs when presented with suitable storm precipitation
and related soil and physiographic characteristics of the basin.
The model is deterministic because the stream channel routing component
is calculated with the Muskingum-Cunge method, which simulates the diffusion wave model
(Ponce and Simons, 1977; Ponce and Yevjevich, 1979). In this method, the time of travel K is based on
Seddon's law (Seddon, 1900).
Moreover, the weighting factor X is based on Hayami's hydraulic diffusivity
and on Cunge's numerical diffusion coefficient (Hayami, 1951; Cunge, 1969).
This methodology provides two distinct advantages: -
The routing parameters are based on hydraulic properties of the basin, including unit-width discharge, bottom slope, and cross-sectional characteristics,
rather than on hydrologic measurements; and
- The calculation is
independent of the chosen grid
specification, within proper limits.
The first advantage enables accurate stream channel routing, whether the streams are gaged or not, and for the full range of all
possible flood events.
The second advantage implies that the calculation is consistent with the governing differential
equations, since one result is repeatedly obtained regardless of the grid specification.
The model is conceptual because the hydrologic abstraction component
is calculated with the NRCS runoff curve number method, which simulates the conceptual filling of the soil reservoir (NRCS, 1984; Ponce, 1996).
Unlike the classical Hortonian approach, which features infinite infiltration,
in the NRCS method infiltration depth approaches asymptotically a constant value (the potential maximum retention S) as the storm increases in size
(Horton, 1933; Natural Resources Conservation Service, 1954).
Experience with the curve number method indicates that it is best suited for infiltration modeling under event [storm] conditions.
Its wide applicability is attributed
to its distinct conceptual basis, although reasonable care is necessary in order to use the method effectively.
The model is distributed because it is able to calculate flood flows, as they vary in space and time
throughout the basin, at any point in the stream network
where an upland subbasin collects its drainage, or where two reach subbasins join together (Fig. 4).
The number of locations where results can be obtained depends on the basin subdivision.
Typical values for the number of subbasins varies from 10 to 100, with the data needs increasing as the number of subbasins increases (Ponce et al., 1985).
| Fig. 4
Cerro Lajas de Tongon, near the confluence of the Moyan and Sangana rivers, La Leche basin.
|
The model is event-driven because it simulates flood flows in situations where direct runoff constitutes the majority of the runoff, i.e., where baseflow
is small and does not appreciably contribute to the flood peak.
Unlike continuous modeling, event-driven modeling does not require long-term [error-prone] moisture accounting.
Thus, results of event-driven flood simualtions are consequent with typical variations in parameter ranges.
Moreover,
the model's unique generalized topological structure enables it to consider a dendritic basin of any order.
Flood hydrographs are seamlessly calculated and expressed at any desired point along the stream network.
The model is a rainfall-runoff model because it seeks, through a suitable transform, to convert effective rainfall (mm) into runoff
(m3/s).
The transform is accomplished by convoluting the NRCS unit hydrograph with the effective storm pattern, to obtain the flood hydrograph
at each subbasin outlet (Natural
Resources Conservation Service, 1954).
The applicability of the NRCS unit hydrograph for rainfall-runoff transform in midsize basins, i.e, those with drainage areas ranging from 1 to
1000 km2, such as those of the La Leche river, has been thoroughly documented (Ponce, 1989).
The model is computational because its discretizes the governing equations of mass and momentum conservation
in the space-time domain by using a suitable numerical scheme. The latter is subject to stability and convergence requirements.
Stability refers to the ability of the scheme to march in time without generating unbounded error growth.
Convergence refers to the ability of the scheme to reproduce the terms of the differential equation
with sufficient accuracy.
The differential equations
are expressed in finite difference form, by using space and time intervals Δx and Δt, respectively. The numerical
properties of the model depend on the proper choice of spatial and temporal resolution. As such,
the Courant law is seen to govern, not only the stability but also the convergence of
numerical schemes of hyperbolic systems of partial differential equations.
In summary, the RAINFLO© model is based on more than fifty
years of research on hydrologic processes, including abstraction (with the runoff curve number),
rainfall-runoff transform (with the NRCS unit hydrograph), and
stream channel routing (with the Muskingum-Cunge method). The combination of deterministic/conceptual methods of relevant hydrologic processes
renders the model particularly predictive.
6. DATA COLLECTION
The data needs are the following:
- Basin topology.
- Subbasin geometric properties.
- Average terrain slopes.
- Storm precipitation.
- Hydrologic soil groups.
- Manning's n roughness coefficients.
- Stream channel cross sections.
6.1 Basin topology
The La Leche basin, from headwaters to La Calzada, is divided into nine (9) upland subbasins and seventeen (17) reach subbasins,
for a total of twenty-six (26) subbasins (Fig. 4).
Runoff in the subbasins can be local or imported. Local runoff originates within each [upland or reach] subbasin, and it is calculated by
convolution of the unit hydrograph (NRCS method).
Imported runoff originates upstream of a reach subbasin, and it is routed through the reach using the Muskingum-Cunge method.
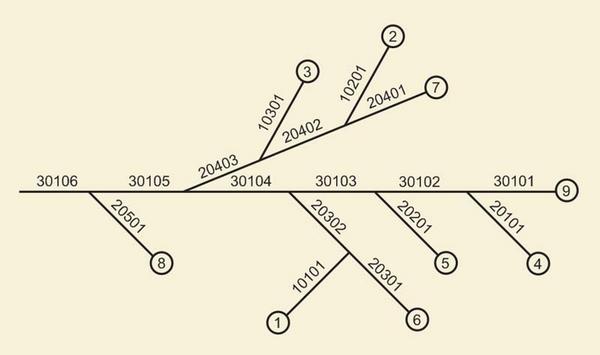
Upland subbasins are numbered consecutively [from 1 to 9] in order of increasing neighboring reach subbasin.
Reach subbasins are numbered, from upstream to downstream, within each stream order, using a 5-digit [order-branch-reach] topological number (Fig. 5).
|
Fig. 5 Topology of the La Leche basin.
|
6.2 Subbasin properties
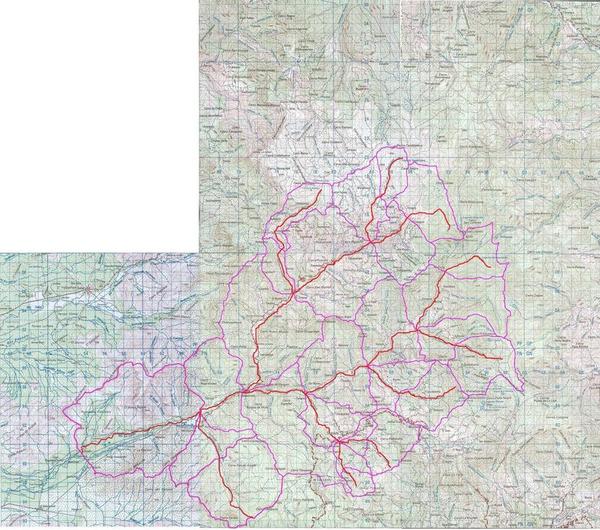
The subbasin geometric properties are obtained from 1:100,000 scale topographic maps (IGN Incahuasi and Jayanca sheets) (Fig. 6).
Geographic features are shown in Table 3.
Drainage areas are delineated following the peaks and saddles of the topography.
Hydraulic lengths and channel slopes are obtained from the maps.
Hydrologic properties are shown in Table 4.
The drainage areas vary from a low of 708 ha (Quebrada del Verde) to a high of
8,815 ha (Rio Moyan 3), with an average of 3,490 ha. The total drainage area for the La Leche river at La Calzada is 90,736 ha, or 907.36
km2.
The hydraulic length of the Moyan/La Leche river, from headwaters to proposed damsite is 44,397 m.
The hydraulic length of the Sangana/La Leche river is 44,591 m. The average channel slope varies from a high of 0.24 for Quebrada Cascabamba
(upland subbasin 6), to a low of 0.01 for Rio La Leche 2, immediately upstream of the damsite (reach subbasin 30106).
|
Fig. 6 The La Leche basin, showing stream network
in red and subbasin boundaries in purple.
|
| Table 3. Subbasin geographic features. |
Topological
number
| Subbasin
| Tributaries
| Lagoons
| Hills
| Towns or
hamlets
|
| 1
| Quebrada Pichucirca
| -
| -
| Chuchupón, Pichucirca
| Yaque
|
| 2
| Quebrada de Tembladera
| -
| Tembladera
| Tembladera, Negro
| La Tranca
|
| 3
| Quebrada de Punguyjo
| Unnamed
| Hualtaco
| Chayapa, Hualtaco
| Sosopampa, Punguyjo, Mushcalin
|
| 4
| Quebrada Cincate (Colán)
| Several unnamed
| -
| Carrampón, Pan de Azúcar, Quiligán, Campana, Cerezo
| - |
| 5
| Quebrada Los Cuartos
| Unnamed
| Totoral, Conrabo, Conchampa
| El Chunque, Pozo Colorado, Verdes de Montaña, Pozo Negro, Mishahuanga
| Caluncate, Sinchabuelito |
| 6
| Quebrada de Cascabamba
| Several unnamed
| -
| Portachuelo de Chapunis, Mishahuanga
| Chapunis, Cachil |
| 7
| Quebrada Huanga Changa
| Quebrada del Verde
| -
| Paltarume, Pichu, Pincuyo, Cunamis
| Chonta Cruz, Miracosta, Yaque, Tallacirca |
| 8
| Río Moyán 0
| Unnamed
| Unnamed
| Lipiag, Choicopico, Negro
| Sinchagual, Tongula |
| 9
| Río Sangana 0
| Several unnamed
| Quinsacocha, three unnamed
| San Lorenzo, Choicopico
| Tucto |
| 10101
| Quebrada Pichucirca
| Unnamed
| -
| Chuchupón
| - |
| 10201
| Quebrada de Tembladera
| Q. Marayhuaca, Q. Ticuaca
| Chapa, Riquiche, Yachapa
| -
| Marayhuaca, Tasajera, Tolospampa, Tingo, Atumpuqio, Piedra Parada |
| 10301
| Quebrada Rachichuela
| -
| -
| Tamboñi
| Tamboñi, Hacienda Moyan |
| 10401
| Quebrada Cincate (Colán)
| Several unnamed
| -
| Carrampón, sin nombre, Calaboso
| Hacienda Mochumi |
| 20101
| Río Chauchaquis
| Q. Unican, Q. Chorro Blanco
| -
| El Chunque, Portachuelo de Chapunis, Segse
| Achucala |
| 20201
| Río Cascabamba (Nieves)
| -
| -
| Chilihuisa, Portachuelo de Chapunis, Huambaracirca
| Nieves, Huambara |
| 20301
| Quebrada del Verde
| -
| -
| Cunamis,
| Yaque, Llacaden |
| 20302
| Río Tocmoche
| Several unnamed
| -
| Chillón, Cunamis, Tres Huacas, Cruz Verde, Gallo
| Luscapampa, Tocmoche, Tangasca |
| 20401
| Río Moyán 1
| Q. Habas, unnamed
| -
| Cochapampa, Rumichaca, Paquican, Pigonta, Atumpampa, Chapa
| Huasicaj, Machaycaj, Shangapampa, Shita, Incahuasi, Cochapampa, Tingo, Tolospampa, Capilla, Totora, Huarhuar |
| 20402
| Río Moyán 2
| Q. de Lanchipampa, Q. Janque, Several unnamed
| -
| Yachapa, Riquiche, Ayumpampa, Pigonta, Lungan, Sopa, Palayon, Pin Pin, San Nicolás,
Viscacha, Puycate, Huacarume
| Atumpuqio, Ullurpampa, Cochapampa, Atumpampa, Lanchipampa, Tallapampa, Sopa, Huayrol, Sacca, Riopampa, Uyshahuasi, Cumba, Amusuy, Ayamachay |
| 20403
| Río Moyán 3
| Q. Cuta, Q. Shahuindo, Several unnamed
| -
| Palayón,
Shugocaga, Nuevo Mundo, Lajas de Tongón, Reloj, Chacuapampa, La Punta, Luycho Potrero, Tamboñi
| El Molino, Tamboni, Pirgacirca, Naranjo, Laquipampa, Lajas, Limón, Zapote, Escalera |
| 30101
| Río Sangana 1
| Q. Pozo con Rabo, unnamed
| -
| Segse, Paquicán, Rumichaca
| Rumichaca, Paccha, El Reloj, Sangana, Congona, Tucto |
| 30102
| Río Sangana 2
| Q. de Minas o de Paquicán, Chilihuisa, Several unnamed
| -
| Pigonta, Chilihuisa, Pumpe, Lungán
| Sangana, Huilsca, Huaysso, Estancia, Succha, Lungán |
| 30103
| Río Sangana 3
| Q. Anguyaco, Q. Shambo, Q, Caracucho
| -
| Sopa, Pumpe, Huambaracirca, Cunamis, Chillón, Gallo, Palayón
| Shashala, Angulis, Chonta, Huambara, Paional, San Martín, Shambo, Caracucho |
| 30104
| Río Sangana 4
| Q. Cruz Verde (Río Seco)
| -
| Zapallar, Cruz Verde, Tres Huacas, Chuchupón, De los Loros, Tasajeras, Quiligán, Carrampón, Pampa de Mula, Lajas de Tongón
| Tangasca, Tres Huacas, Llaves |
| 30105
| Río La Leche 1
| Q. Negrahuasi (Del Reloj), unnamed
| -
| Reloj, Negrahuasi
| El Campamento, La U, Puchaca |
| 30106
| Río La Leche 2
| Q. La Calera, Q. Medio Mundo, Q. Calabozo, Several unnamed
| -
| La Calera, Calaboso, Motupillo, La Traposa, Calicantro, Huaca Rajada, Jahuay Negro, San Antonio, Guineal, Carpintero,
Pasato Quemado
| La Calera, La Calzada, Mochumi Viejo, Mayascón, La Traposa, Papayo Desaguadero, Motupillo, San Juan,
Calicantro |
|
| Table 4. Subbasin hydrologic properties. |
Topological
number
| Subbasin
| Drainage
area
(ha)
| Hydraulic
length
(m)
| Average
channel slope
(m/m)
|
| 1
| Quebrada Pichucirca
| 709.09
| 3816.2
| 0.1347
|
| 2
| Quebrada de Tembladera
| 1517.07
| 5316.5
| 0.0707
|
| 3
| Quebrada de Punguyjo
| 2215.85
| 9231.3
| 0.1213
|
| 4
| Quebrada Cincate (Colán)
| 5968.65
| 8179.1
| 0.0550
|
| 5
| Quebrada Los Cuartos
| 3379.84
| 5304.7
| 0.1546
|
| 6
| Quebrada de Cascabamba
| 3121.00
| 6745.8
| 0.2372
|
| 7
| Quebrada Huanga Changa
| 2645.08
| 4030.7
| 0.0610
|
| 8
| Río Moyán 0
| 3385.71
| 6251.3
| 0.1392
|
| 9
| Río Sangana 0
| 3095.34
| 5756.2
| 0.0695
|
| 10101
| Quebrada Pichucirca
| 788.88
| 3026.3
| 0.0634
|
| 10201
| Quebrada de Tembladera
| 3082.88
| 5551.7
| 0.1214
|
| 10301
| Quebrada Rachichuela
| 1245.12
| 9301.9
| 0.1199
|
| 10401
| Quebrada Cincate (Colán)
| 2552.32
| 5413.6
| 0.0074
|
| 20101
| Río Chauchaquis
| 2337.49
| 4488.0
| 0.1404
|
| 20201
| Río Cascabamba (Nieves)
| 2130.89
| 4525.2
| 0.1496
|
| 20301
| Quebrada del Verde
| 708.49
| 3009.3
| 0.0847
|
| 20302
| Río Tocmoche
| 2340.41
| 6869.6
| 0.1057
|
| 20401
| Río Moyán 1
| 3357.12
| 5020.2
| 0.0558
|
| 20402
| Río Moyán 2
| 8647.12
| 10332.8
| 0.1050
|
| 20403
| Río Moyán 3
| 8815.68
| 13908.7
| 0.0737
|
| 30101
| Río Sangana 1
| 5284.21
| 7427.8
| 0.1077
|
| 30102
| Río Sangana 2
| 4486.57
| 7636.2
| 0.0864
|
| 30103
| Río Sangana 3
| 5567.31
| 7974.7
| 0.0722
|
| 30104
| Río Sangana 4
| 6426.92
| 6886.5
| 0.0398
|
| 30105
| Río La Leche 1
| 4307.96
| 5333.9
| 0.0244
|
| 30106
| Río La Leche 2
| 2619.12
| 3550.5
| 0.0099
|
| Total
| Río La Leche at La Calzada
| 90736.12
| -
| -
|
|
6.3 Terrain slopes
The terrain slopes across the La Leche basin were sampled on a 1-km2 grid.
Average terrain slopes are shown in Table 5. Average terrain slopes vary from a low of 19.7% in Quebrada Tembladera to a high of 50.3% in Rio
Sangana 2, with an average of 33.7% for the entire La Leche basin to La Calzada (Fig. 7).
| Table 5. Subbasin average terrain slopes. |
| Topological number
| Subbasin
| Map correction
| Number of sampling points
| Average distance between curves
| Average distance (m)
| Average terrain slope
(%)
|
| [1]
| [2]
| [3]
| [4]
| [5] =
Σ Di /[4]
| [6] =
1000 * [5]/[3]
| [7] =
100 * 50/[6]
|
| 1
| Quebrada Pichucirca
| 1.0332
| 9
| 0.150
| 145.180
| 34.41
|
| 2
| Quebrada de Tembladera
| 1.0403
| 15
| 0.199
| 191.291
| 26.18
|
| 3
| Quebrada de Punguyjo
| 1.0411
| 22
| 0.159
| 152.723
| 32.84
|
| 4
| Quebrada Cincate (Colán)
| 1.0402
| 59
| 0.208
| 199.962
| 24.96
|
| 5
| Quebrada Los Cuartos
| 1.046
| 35
| 0.132
| 126.195
| 39.62
|
| 6
| Quebrada de Cascabamba
| 1.0395
| 32
| 0.172
| 165.464
| 30.27
|
| 7
| Quebrada Huanga Changa
| 1.0406
| 26
| 0.168
| 161.445
| 30.95
|
| 8
| Río Moyán 0
| 1.0449
| 34
| 0.175
| 167.480
| 29.77
|
| 9
| Río Sangana 0
| 1.036
| 31
| 0.153
| 147.683
| 33.78
|
| 10101
| Quebrada Pichucirca
| 1.0351
| 6
| 0.240
| 231.862
| 21.55
|
| 10201
| Quebrada de Tembladera
| 1.038
| 30
| 0.263
| 253.372
| 19.72
|
| 10301
| Quebrada Rachichuela
| 1.0332
| 12
| 0.113
| 109.369
| 45.71
|
| 10401
| Quebrada Cincate (Colán)
| 1.0527
| 25
| 0.241
| 228.935
| 21.81
|
| 20101
| Río Chauchaquis
| 1.0328
| 24
| 0.138
| 133.617
| 37.53
|
| 20201
| Río Cascabamba (Nieves)
| 1.036
| 23
| 0.184
| 177.606
| 28.12
|
| 20301
| Quebrada del Verde
| 1.0408
| 7
| 0.197
| 189.277
| 26.40
|
| 20302
| Río Tocmoche
| 1.0344
| 24
| 0.160
| 154.679
| 32.35
|
| 20401
| Río Moyán 1
| 1.0383
| 35
| 0.148
| 142.541
| 35.08
|
| 20402
| Río Moyán 2
| 1.0303
| 88
| 0.137
| 132.971
| 37.70
|
| 20403
| Río Moyán 3
| 1.041
| 86
| 0.110
| 105.668
| 47.44
|
| 30101
| Río Sangana 1
| 1.0452
| 46
| 0.121
| 115.767
| 43.02
|
| 30102
| Río Sangana 2
| 1.0285
| 45
| 0.102
| 99.174
| 50.28
|
| 30103
| Río Sangana 3
| 1.0371
| 54
| 0.112
| 107.993
| 46.32
|
| 30104
| Río Sangana 4
| 1.0412
| 63
| 0.180
| 172.877
| 28.88
|
| 30105
| Río La Leche 1
| 1.0465
| 44
| 0.179
| 171.046
| 29.16
|
| 30106
| Río La Leche 2
| 1.0441
| 25
| 0.125
| 119.720
| 41.66
|
| Average
| Río La Leche
| -
| -
| -
| -
| 33.69
|
|
 |
|
Fig. 7 Typical steep slopes of the Moyan/La Leche watershed. |
6.4 Storm precipitation
The storm precipitation for flood modeling is defined in terms of depth, duration, type, and frequency.
The hydraulic length in the La Leche basin is approximately 45,000 m.
Given the high roughness present in most of the stream channels, mean velocities during flood events average 3 to 4 m/s.
Therefore, the time of concentration varies between 3 to 4 hr. The chosen storm duration for design is 24 hr, to follow established
hydrologic practice (Ponce, 1989). In fact, NRCS 24-hr type storms contain the shorter storms, ranging from 0.5 hr to 12 hr.
To choose a suitable type storm, the climatology and geographic features
of the La Leche basin are compared with the four regions in the United States where design type storms
have been developed by NRCS. The Type I storm, applicable to Southern and Central Coastal California,
an arid/semiarid region in close proximity to the Pacific Ocean but with significant orographic features,
is judged to best resemble local/regional conditions. Therefore, the Type I storm is chosen to simulate
floods in the La Leche basin.
In the case of basins such as that of La Leche, where suitable generalized [absolute envelopes of] Probable Maximum Precipitation (PMP) are not available,
it is common practice to substitute the 10,000-yr return period for the PMP.
Therefore, design storm precipitation for large dams in the La Leche basin is as follows (Natural Resources Conservation Service, 1986; Ponce, 1989):
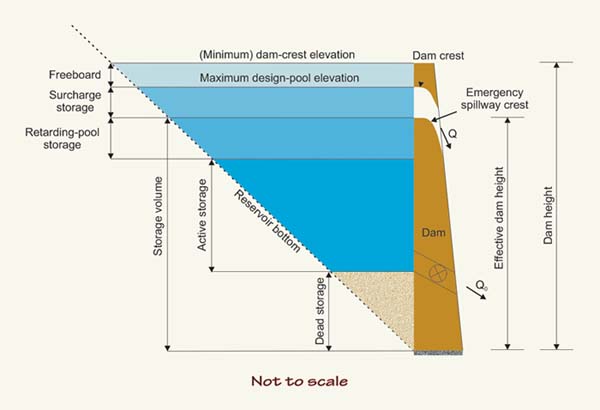
The principal spillway hydrograph is used to determine:
(1) the capacity of the principal spillway,
(2) the emergency spillway crest elevation, and
(3) the volume of retarding pool storage.
The emergency spillway hydrograph is used to determine:
(1) the capacity of the emergency spillway,
(2) the maximum design pool elevation, and
(3) the volume of surcharge storage.
The freeboard hydrograph is used to determine the minimum dam crest elevation (freeboard), and
to evaluate the structural integrity of the spillway system (Fig. 8).
|
Fig. 8 Definition sketch for reservoir storage volumes (Ponce, 1989).
|
The 24-hr annual maximum storm precipitation records for the Puchaca, Tocmoche, and Incahuasi stations, up to 1998, were obtained
from Perez Becerra (2006). The ordered values are shown in Table 6. The record for the period 1999-2007 remains to be collected.
| Table 6. 24-hr annual maximum storm precipitation in La Leche stations
1 |
| Order
| Puchaca
| Tocmoche
| Incahuasi
|
| 1
| 4.2
| 5.2
| 17.0
|
| 2
| 6.1
| 7.0
| 20.0
|
| 3
| 7.2
| 10.0
| 20.5
|
| 4
| 8.2
| 12.0
| 21.0
|
| 5
| 8.5
| 12.0
| 21.5
|
| 6
| 8.8
| 15.0
| 21.5
|
| 7
| 9.7
| 20.0
| 21.5
|
| 8
| 11.1
| 20.0
| 22.0
|
| 9
| 12.9
| 20.0
| 24.0
|
| 10
| 14.3
| 25.0
| 25.5
|
| 11
| 20.3
| 25.0
| 25.5
|
| 12
| 23.2
| 25.0
| 25.5
|
| 13
| 24.3
| 28.0
| 26.2
|
| 14
| 27.5
| 30.0
| 28.0
|
| 15
| 30.0
| 32.0
| 28.0
|
| 16
| 30.2
| 35.0
| 30.5
|
| 17
| 30.3
| 35.0
| 30.7
|
| 18
| 31.5
| 36.0
| 31.5
|
| 19
| 33.5
| 40.0
| 33.0
|
| 20
| 40.0
| 40.0
| 33.5
|
| 21
| 40.1
| 45.0
| 33.5
|
| 22
| 51.5
| 45.0
| 34.0
|
| 23
| 58.4
| 47.0
| 34.0
|
| 24
| 59.0
| 48.0
| 34.5
|
| 25
| 60.0
| 55.0
| 34.5
|
| 26
| 60.2
| 55.0
| 36.0
|
| 27
| 60.3
| 60.0
| 36.6
|
| 28
| 60.9
| 60.0
| 37.0
|
| 29
| 62.7
| 61.0
| 39.0
|
| 30
| 65.3
| 70.0
| 40.5
|
| 31
| 95.4
| 76.0
| 43.5
|
| 32
| 96.2
| 85.0
| 45.0
|
| 33
| 100.4
| 94.0
| 52.0
|
| 34
| 101.5
| 100.0
| 53.0
|
| 35
| 150.0
| 100.4
| 55.0
|
| 36
| 150.2
| -
| 81.0
|
| 1 24-hr annual maximum storm precipitation in mm.
|
|
6.5 Hydrologic soil groups
The hydrologic soil groups for the La Leche basin have been estimated by Consorcio Salzgitter-Lagesa (1984) as D for the
upper basin, and B for the middle and lower basin. Perez Becerra (2006) has estimated
hydrologic soil groups as varying between B, C, and D, with three types of land uses: (1) impermeable soil or rock, (2) pasture, and (2) shrub.
The average of 28 subbasins considered in the Perez Becerra study is CNII = 85.
On a preliminary basis, and pending field verification, the hydrologic soil group for the entire La Leche basin is estimated as D (rock outcrops and clay soil).
The predominant land use is mixed woodland/grassland and cropland (Fig. 9).
The adopted CNII values were obtained from Ponce (1989).
The percent aerial coverage and hydrologic surface condition
were estimated using Google Earth Pro© software.
Fig. 9 Cropland in the Moyan watershed.
|
Weighted CNII values are shown in Table 7.
The [aerial] weighted CNII values shown in this table were weighted with the respective subbasin drainage areas to
obtain a basinwide CNII = 85.
This value compares favorably with those given by Perez Becerra (2006).
Antecedent moisture condition AMCIII is assumed.
Therefore, the corresponding basinwide CNIII = 94 (Ponce, 1989).
The assumed hydrologic soil groups and hydrologic surface conditions will be checked in the field prior to the completion of this study.
Table 7.
Subbasin runoff curve numbers.
| Topological number
| Subbasin
| Hydrologic soil group
| Land use
| Aerial weighted CNII
|
| Woodland/grassland
| Cropland
|
| Hydrologic surface condition
| CNII
| Percent aerial coverage
| Hydrologic surface condition
| CNII
| Percent aerial coverage
|
| 1
| Quebrada Pichucirca
| D
| good
| 79
| 30
| good
| 89
| 70
| 86
|
| 2
| Quebrada de Tembladera
| D
| good
| 79
| 90
| good
| 89
| 10
| 80
|
| 3
| Quebrada de Punguyjo
| D
| good
| 79
| 70
| good
| 89
| 30
| 82
|
| 4
| Quebrada Cincate (Colán)
| D
| poor
| 86
| 100
| good
| 89
| 0
| 86
|
| 5
| Quebrada Los Cuartos
| D
| good
| 79
| 80
| good
| 89
| 20
| 81
|
| 6
| Quebrada de Cascabamba
| D
| good
| 79
| 40
| good
| 89
| 60
| 85
|
| 7
| Quebrada Huanga Changa
| D
| good
| 79
| 60
| good
| 89
| 40
| 83
|
| 8
| Río Moyán 0
| D
| good
| 79
| 100
| good
| 89
| 0
| 79
|
| 9
| Río Sangana 0
| D
| good
| 79
| 100
| good
| 89
| 0
| 79
|
| 10101
| Quebrada Pichucirca
| D
| good
| 79
| 50
| good
| 89
| 50
| 84
|
| 10201
| Quebrada de Tembladera
| D
| good
| 79
| 80
| good
| 89
| 20
| 81
|
| 10301
| Quebrada Rachichuela
| D
| poor
| 86
| 80
| good
| 89
| 20
| 87
|
| 10401
| Quebrada Cincate (Colán)
| D
| poor
| 86
| 100
| good
| 89
| 0
| 86
|
| 20101
| Río Chauchaquis
| D
| good
| 79
| 70
| good
| 89
| 30
| 82
|
| 20201
| Río Cascabamba (Nieves)
| D
| good
| 79
| 70
| good
| 89
| 30
| 82
|
| 20301
| Quebrada del Verde
| D
| good
| 79
| 20
| good
| 89
| 80
| 87
|
| 20302
| Río Tocmoche
| D
| good
| 79
| 80
| good
| 89
| 20
| 81
|
| 20401
| Río Moyán 1
| D
| good
| 79
| 80
| good
| 89
| 20
| 81
|
| 20402
| Río Moyán 2
| D
| poor
| 86
| 80
| good
| 89
| 20
| 87
|
| 20403
| Río Moyán 3
| D
| fair
| 82
| 80
| good
| 89
| 20
| 83
|
| 30101
| Río Sangana 1
| D
| fair
| 82
| 80
| good
| 89
| 20
| 83
|
| 30102
| Río Sangana 2
| D
| poor
| 86
| 90
| good
| 89
| 10
| 86
|
| 30103
| Río Sangana 3
| D
| good
| 79
| 80
| good
| 89
| 20
| 81
|
| 30104
| Río Sangana 4
| D
| fair
| 82
| 100
| good
| 89
| 0
| 82
|
| 30105
| Río La Leche 1
| D
| fair
| 82
| 90
| good
| 89
| 10
| 83
|
| 30106
| Río La Leche 2
| D
| poor
| 86
| 90
| good
| 89
| 10
| 87
|
| Basinwide
| Río La Leche
| -
| -
| -
| -
| -
| -
| -
| 85
| |
|
6.6 Manning's n
Manning's n roughness coefficients shown in Table 8 were based on Barnes (1967).
Observational and other evidence indicates that the La Leche river tributaries are able to move very large boulders, aproaching 1 m in diameter (Fig. 14).
Thus, inbank Manning's n for most reaches are taken as 0.075.
Eight-point cross-sectional data is shown in Tables 8 and 9.
|
| Table 8. Manning's n roughness and other cross-sectional data. |
Topological
number
| Subwatershed
| Number of points
| Manning's n left bank
| Manning's n center channel
| Manning's n right bank
| x-coordinate left/center
| x-coordinate center/right
|
| 10101
| Quebrada Pichucirca
| 8
| 0.100
| 0.080
| 0.100
| 114
| 121
|
| 10201
| Quebrada de Tembladera
| 8
| 0.100
| 0.075
| 0.100
| 116
| 126
|
| 10301
| Quebrada Rachichuela
| 8
| 0.100
| 0.075
| 0.100
| 114
| 123
|
| 10401
| Quebrada Cincate (Colán)
| 8
| 0.100
| 0.035
| 0.100
| 196
| 224
|
| 20101
| Río Chauchaquis
| 8
| 0.100
| 0.075
| 0.100
| 116
| 126
|
| 20201
| Río Cascabamba (Nieves)
| 8
| 0.100
| 0.075
| 0.100
| 114
| 123
|
| 20301
| Quebrada del Verde
| 8
| 0.100
| 0.075
| 0.100
| 114
| 123
|
| 20302
| Río Tocmoche
| 8
| 0.100
| 0.075
| 0.100
| 131
| 143
|
| 20401
| Río Moyán 1
| 8
| 0.100
| 0.075
| 0.100
| 131
| 143
|
| 20402
| Río Moyán 2
| 8
| 0.100
| 0.075
| 0.100
| 131
| 147
|
| 20403
| Río Moyán 3
| 8
| 0.100
| 0.075
| 0.100
| 131
| 149
|
| 30101
| Río Sangana 1
| 8
| 0.100
| 0.075
| 0.100
| 131
| 143
|
| 30102
| Río Sangana 2
| 8
| 0.100
| 0.075
| 0.100
| 131
| 147
|
| 30103
| Río Sangana 3
| 8
| 0.100
| 0.075
| 0.100
| 131
| 149
|
| 30104
| Río Sangana 4
| 8
| 0.09
| 0.07
| 0.09
| 146
| 168
|
| 30105
| Río La Leche 1
| 8
| 0.08
| 0.06
| 0.08
| 196
| 228
|
| 30106
| Río La Leche 2
| 8
| 0.07
| 0.04
| 0.07
| 196
| 244
|
|
6.7 Cross-sectional geometry
Data on typical cross sections is currently being collected.
Pending field verification,
typical cross sections were estimated for all reach subbasin stream channels using stream order and subbasin drainage areas,
supported with field observations and experience. Eight-point estimated typical cross-sectional data is shown in Tables 8 and 9.
| Table 9. Typical reach eight-point cross-sectional data. |
Topological
number
| Subbasin
| x1
| z1
| x2
| z2
| x3
| z3
| x4
| z4
| x5
| z5
| x6
| z6
| x7
| z7
| x8
| z8
|
| 10101
| Quebrada Pichucirca
| 100
| 120
| 108
| 112
| 114
| 109
| 115
| 108
| 120
| 108
| 121
| 109
| 127
| 112
| 135
| 120
|
| 10201
| Quebrada de Tembladera
| 100
| 120
| 108
| 112
| 116
| 108
| 118
| 106
| 124
| 106
| 126
| 108
| 134
| 112
| 142
| 120
|
| 10301
| Quebrada Rachichuela
| 100
| 120
| 108
| 112
| 114
| 109
| 116
| 107
| 121
| 107
| 123
| 109
| 129
| 112
| 137
| 120
|
| 10401
| Quebrada Cincate (Colán)
| 100
| 120
| 116
| 112
| 196
| 104
| 200
| 102
| 220
| 102
| 224
| 104
| 304
| 112
| 320
| 120
|
| 20101
| Río Chauchaquis
| 100
| 120
| 108
| 112
| 116
| 108
| 118
| 106
| 124
| 106
| 126
| 108
| 134
| 112
| 142
| 120
|
| 20201
| Río Cascabamba (Nieves)
| 100
| 120
| 108
| 112
| 116
| 108
| 118
| 106
| 124
| 106
| 126
| 108
| 134
| 112
| 142
| 120
|
| 20301
| Quebrada del Verde
| 100
| 120
| 108
| 112
| 114
| 109
| 116
| 107
| 121
| 107
| 123
| 109
| 129
| 112
| 137
| 120
|
| 20302
| Río Tocmoche
| 100
| 120
| 116
| 112
| 131
| 107
| 133
| 105
| 141
| 105
| 143
| 107
| 158
| 112
| 174
| 120
|
| 20401
| Río Moyán 1
| 100
| 120
| 116
| 112
| 131
| 107
| 133
| 105
| 141
| 105
| 143
| 107
| 158
| 112
| 174
| 120
|
| 20402
| Río Moyán 2
| 100
| 120
| 116
| 112
| 131
| 107
| 134
| 104
| 144
| 104
| 147
| 107
| 162
| 112
| 178
| 120
|
| 20403
| Río Moyán 3
| 100
| 120
| 116
| 112
| 131
| 107
| 134
| 104
| 146
| 104
| 149
| 107
| 164
| 112
| 180
| 120
|
| 30101
| Río Sangana 1
| 100
| 120
| 116
| 112
| 131
| 107
| 133
| 105
| 141
| 105
| 143
| 107
| 158
| 112
| 174
| 120
|
| 30102
| Río Sangana 2
| 100
| 120
| 116
| 112
| 131
| 107
| 134
| 104
| 144
| 104
| 147
| 107
| 162
| 112
| 178
| 120
|
| 30103
| Río Sangana 3
| 100
| 120
| 116
| 112
| 131
| 107
| 134
| 104
| 146
| 104
| 149
| 107
| 164
| 112
| 180
| 120
|
| 30104
| Río Sangana 4
| 100
| 120
| 116
| 112
| 146
| 106
| 149
| 103
| 165
| 103
| 168
| 106
| 198
| 112
| 214
| 120
|
| 30105
| Río La Leche 1
| 100
| 120
| 116
| 112
| 196
| 104
| 202
| 101
| 222
| 101
| 228
| 104
| 308
| 112
| 324
| 120
|
| 30106
| Río La Leche 2
| 100
| 120
| 116
| 112
| 196
| 104
| 202
| 101
| 238
| 101
| 244
| 104
| 324
| 112
| 340
| 120
|
|
7. STORM FREQUENCY MODELING
Storm frequency modeling was accomplished using the Log Pearson III and Gumbel methods (U.S. Interagency Advisory Committee on Water Data, 1983; Ponce, 1989).
The [measured] values shown in Table 6 were used to calculate 100-yr and 10,000-yr 24-hr storms for the three stations: Puchaca, Tocmoche, and Incahuasi.
These values are shown in Table 10, together with the adopted values, taken as the average of the two methods. Also shown in Table 10 are the
applicable 24-storm precipitation for the principal spillway, emergency spillway, and freeboard hydrographs (Section 6.4).
| Table 10. Storm precipitation in La Leche climatological
stations.1
|
| Method
| Return period (yr)
| Station
| Puchaca 2
| Tocmoche 3
| Incahuasi 4
|
| Log Pearson III
| 100
| 229
| 131
| 78
|
| 10000
| 565
| 202
| 167
|
| Gumbel
| 100
| 184
| 137
| 78
|
10000
| 340
| 245
| 130
| Adopted
| 100
| 207
| 134
| 78
|
| 10000
| 453
| 224
| 149
| Ppsh (principal spillway hydrograph)
| 207
| 134
| 78
|
| Pesh (emergency spillway hydrograph)
| 271
| 157
| 96
|
| Pfbh (freeboard hydrograph)
| 453
| 224
| 149
|
1 24-hr storm precipitation in mm.
2 Elevation = 355 m.a.m.s.l.
3 Elevation = 1,450 m.a.m.s.l.
4 Elevation = 3,078 m.a.m.s.l.
|
|
|
For each subbasin, 24-hr design storm precipitations
were obtained by logarithmic interpolation, in reference to the elevation-storm data calculated for the stations at Puchaca, Tocmoche, and Incahuasi
(Table 10). Design storm precipitations are shown in Table 11.
The design storm precipitations were weighted with the respective drainage areas
to calculate the basinwide storm precipitations shown in the last row of Table 11.
| Table 11. Design storm precipitations.
|
Topological
number
| Subbasin
| Drainage area
(ha)
| Elevation
of centroid
(m)
| P100
(mm)
| P10000
(mm)
| Ppsh
(mm)
| Pesh
(mm)
| Pfbh
(mm)
|
| 1
| Quebrada Pichucirca
| 709.09
| 2000
| 106.3
| 188.2
| 106
| 128
| 188
|
| 2
| Quebrada de Tembladera
| 1517.07
| 3550
| 70.4
| 137.9
| 70
| 88
| 138
|
| 3
| Quebrada de Punguyjo
| 2215.85
| 3100
| 77.6
| 148.4
| 78
| 96
| 148
|
| 4
| Quebrada Cincate (Colán)
| 5968.65
| 500
| 186.2
| 381.6
| 186
| 237
| 382
|
| 5
| Quebrada Los Cuartos
| 3379.84
| 3500
| 71.1
| 138.9
| 71
| 89
| 139
|
| 6
| Quebrada de Cascabamba
| 3121.00
| 2450
| 91.9
| 168.6
| 92
| 112
| 169
|
| 7
| Quebrada Huanga Changa
| 2645.08
| 1750
| 117.0
| 202.3
| 117
| 139
| 202
|
| 8
| Río Moyán 0
| 3385.71
| 3550
| 70.4
| 137.9
| 70
| 88
| 138
|
| 9
| Río Sangana 0
| 3095.34
| 3050
| 78.5
| 149.7
| 78
| 97
| 150
|
| 10101
| Quebrada Pichucirca
| 788.88
| 1600
| 124.8
| 212.4
| 125
| 148
| 212
|
| 10201
| Quebrada de Tembladera
| 3082.88
| 3300
| 74.2
| 143.5
| 74
| 92
| 144
|
| 10301
| Quebrada Rachichuela
| 1245.12
| 2000
| 106.3
| 188.2
| 106
| 128
| 188
|
| 10401
| Quebrada Cincate (Colán)
| 2552.32
| 350
| 207.9
| 456.2
| 208
| 272
| 456
|
| 20101
| Río Chauchaquis
| 2337.49
| 2700
| 85.7
| 160.0
| 86
| 105
| 160
|
| 20201
| Río Cascabamba (Nieves)
| 2130.89
| 1900
| 110.3
| 193.5
| 110
| 132
| 194
|
| 20301
| Quebrada del Verde
| 708.49
| 1400
| 135.4
| 228.0
| 135
| 159
| 228
|
| 20302
| Río Tocmoche
| 2340.41
| 1100
| 145.9
| 257.2
| 146
| 175
| 257
|
| 20401
| Río Moyán 1
| 3357.12
| 3100
| 77.6
| 148.4
| 78
| 96
| 148
|
| 20402
| Río Moyán 2
| 8647.12
| 2200
| 99.3
| 178.7
| 99
| 120
| 179
|
| 20403
| Río Moyán 3
| 8815.68
| 1600
| 124.8
| 212.4
| 125
| 148
| 212
|
| 30101
| Río Sangana 1
| 5284.21
| 2700
| 85.7
| 160.0
| 86
| 105
| 160
|
| 30102
| Río Sangana 2
| 4486.57
| 2000
| 106.3
| 188.2
| 106
| 128
| 188
|
| 30103
| Río Sangana 3
| 5567.31
| 1100
| 145.9
| 257.2
| 146
| 175
| 257
|
| 30104
| Río Sangana 4
| 6426.92
| 1000
| 150.3
| 270.0
| 150
| 181
| 270
|
| 30105
| Río La Leche 1
| 4307.96
| 600
| 176.0
| 348.3
| 176
| 221
| 348
|
| 30106
| Río La Leche 2
| 2619.12
| 600
| 176.0
| 348.3
| 176
| 221
| 348
|
| Basinwide
| Río La Leche
| 90736.12
| -
| -
| -
| 119
| 146
| 222
|
|
8. MODEL RESULTS
The design storms of Table 11 were used to drive the RAINFLO© model to calculate flood discharges.
The subbasin curve numbers are those shown in Table 7.
The rainfall-runoff transform [NRCS unit hydrograph] was performed using the data of Tables 4 and 5.
Average velocities [along hydraulic lengths] were estimated in the range 3-4 m/s.
The friction and cross-sectional data is shown in Tables 8 and 9.
The model was run for a period of 48 hr, with a time interval of 0.125 hr (7.5 minutes).
To assure the accuracy of the Muskingum-Cunge routing method, the Courant numbers were kept around one (C = 1) by appropriate reach subdivision (Ponce, 1989).
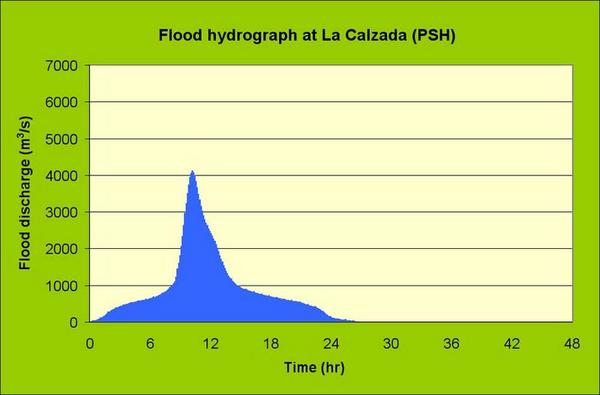
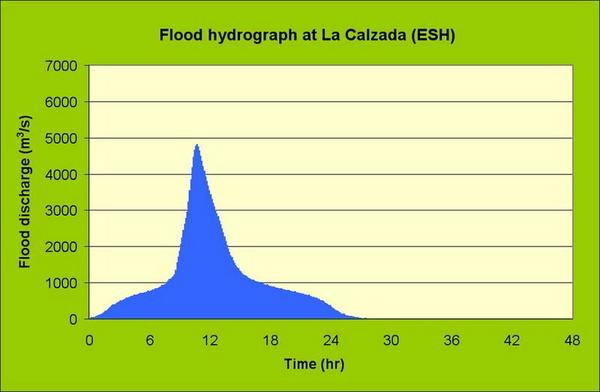
Design flood hydrographs at La Calzada are shown in Figs. 10, 11, and 12.
Table 12 shows a summary of design flood discharges for a high dam at La Calzada.
 |
|
Fig. 10 Principal spillway hydrograph at La Calzada. |
 |
|
Fig. 11 Emergency spillway hydrograph at La Calzada. |
 |
|
Fig. 12 Freeboard hydrograph at La Calzada. |
|
Table 12. Design flood discharges for dam at La Calzada.
|
| Hydrograph
| Flood discharge
(m3/s)
| Hydrograph volume
(hm3)
| Area-weighted
24-hr storm depth
(mm)
| Storm volume
(hm3)
| Runoff
(%)
|
| Principal spillway hydrograph
| 4,108
| 90
| 119
| 108
| 83
|
| Emergency spillway hydrograph
| 4,799
| 114
| 146
| 132
| 86
|
| Freeboard hydrograph
| 6,503
| 182
| 222
| 201
| 91
|
9. WORK IN PROGRESS
Work is in progress to complete the precipitation record for the three stations: Puchaca, Tocmoche, and Incahuasi.
Work is also in progress to verify and complete the hydrologic soil group, hydrologic surface condition, and friction and cross-sectional data.
10. CONCLUSIONS
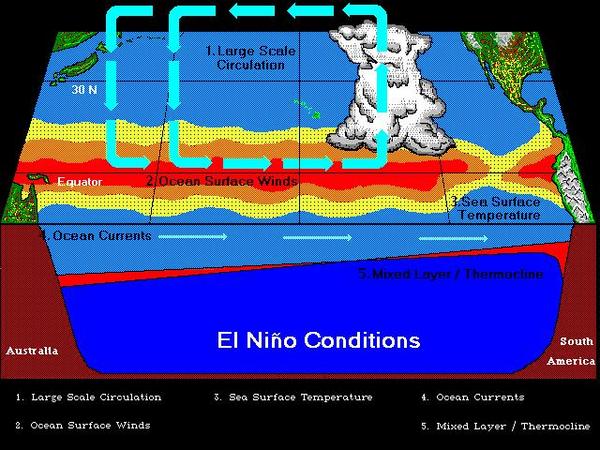
A deterministic/conceptual distributed rainfall-runoff computational model is used to calculate design flood discharges for a proposed
dam in the La Leche river at La Calzada, in Lambayeque, Peru. The model is driven by suitable frecuency-based
24-hr storms which take into account the precipitation record,
including El Niño events (Fig. 13). Geometric, hydrologic, soil, cross-sectional and other data are assembled in suitable form
in order to feed the computational model.
Peak flood discharge, hydrograph volume, storm volume, and percent runoff are calculated for
principal spillway, emergency spillway, and freeboard design (Table 12). These design hydrographs can be used to size the
retarding-pool storage, the surcharge storage, and the freeboard (Fig. 6).
Fig. 13 El Niño conditions along the Equatorial Pacific Ocean (Source: UC Santa Barbara).
|
REFERENCES
Barnes, H. A. 1967. Roughness characteristics of natural channels. U.S. Geological Survey Water-Supply Paper 1849, Washington, D.C.
Consorcio Salzgitter-Lagesa, 1984. Rehabilitación y reconstrucción de los sistemas de riego y drenaje del valle
Chancay-Lambayeque: Estudio de evacuación de avenidas extraordinarias a nivel de factibilidad técnica.
Tomo 1: Resumen e investigaciones básicas, marzo.
Cunge, j. A., 1969. On the subject of a flood propagation computation method (Muskingum method). Journal of Hydraulic Research, Vol. 7, No. 2, 205-230.
DEPOLTI (Dirección Ejecutiva del Proyecto Especial Olmos-Tinajones), 1998.
Actualización de la factibilidad tecnico-económica del embalse en el Río
La Leche, Chiclayo, Peru, 339 p.
Hayami, S., 1951. On the propagation of flood waves. Disaster Prevention Research Institute, Kyoto University, Bulletin, No. 1, December.
Horton, R, E., 1933. The role of infiltration in the hydrologic cycle. Transactions, American Geophysical Union, Vol. 14, 446-460.
Natural Resources Conservation Service, 1985.
Earth dams and reservoirs.
Technical Release No. 60 (TR-60), revised October.
Natural Resources Conservation Service, 1954. National Engineering Handbook No. 4 - Hydrology. Washington, D.C.
Perez Becerra, M. A., 2006. Estudio hidrológico e hidráulico
en el río La Leche: Generación de las descargas y niveles máximos por avenidas
en la zona del proyecto "Puente Colgante Pítipo." Proyecto Especial Olmos-Tinajones, Gerencia de Desarrollo Tinajones, Mayo.
Ponce, V. M., and D. B. Simons, 1977. Shallow wave propagation in open channel flow.
ASCE Journal of Hydraulic Engineering, Vol. 103, No. 12, December.
Ponce, V. M., and V. Yevjevich, 1979. Muskingum-Cunge method with variable parameters.
ASCE Journal of Hydraulic Engineering, Vol. 103, No. 12, December.
Ponce, V. M., 1985. Large basin deterministic hydrology: A case study.
ASCE Journal of Hydraulic Engineering, Vol. 111, No. 9, September.
Ponce, V. M., 1989. Engineering Hydrology, Principles and Practices. Prentice Hall, Englewood Cliffs, New Jersey.
Ponce, V. M., 1996. Runoff curve number: Has it reached maturity?
ASCE Journal of Hydrologic Engineering, Vol. 1, No. 1, January.
Seddon, J. A., 1900. River hydraulics. Transactions, American Society of Civil Engineers, Vol. XLIII, 179-243, June.
U.S. Interagency Advisory Committee on Water Data, 1983. Guidelines for determining flood flow frequency. Hydrology Subcommitee, Bulletin
No. 17B, issued 1981, revised 1983, Reston, Virginia.
Fig. 14 The Moyan river, showing very large boulders on the streambed.
|
|