| CAP�TULO 5: ESCOAMENTO UNIFORME |
5.1 ESCOAMENTO UNIFORME
O fluxo uniforme � estritamente aplic�vel apenas em canais prism�ticos. No fluxo uniforme, a profundidade do fluxo, a �rea do fluxo, a velocidade m�dia e a vazão s�o constantes ao longo do canal. Para canais n�o-prism�ticos (naturais) de se��o transversal quase uniforme, o termo fluxo de equil�brio � frequentemente usado para descrever a condi��o de fluxo que se aproxima ou se assemelha ao fluxo uniforme de canais prism�ticos.
Em um escoamento uniforme, todas as declividades (de atrito Sf, de energia Se, da superf�cie da água Sw e do leito So) s�o constantes e iguais à declividade S.
Sf = Se = Sw = So = S
| (5-1) |
N�o existe escoamento uniforme e inst�vel. Se o fluxo � inst�vel, ele simplesmente n�o � uniforme.
Estabelecimento de escoamento uniforme
Do ponto de vista mec�nico, o fluxo uniforme ocorre em um volume de controle quando a for�a de atrito � igual � for�a gravitacional. Na aus�ncia de controles de se��o (Seção 4.3), todos os fluxos de canais tendem naturalmente a ter escoamento uniforme.
No fluxo uniforme, a propriedade única da área da curva-chave da vazão ou profundidade qualifica o fluxo uniforme como um controle do canal. Assim, o fluxo cr�tico uniforme � muito significativo no controle de canais.
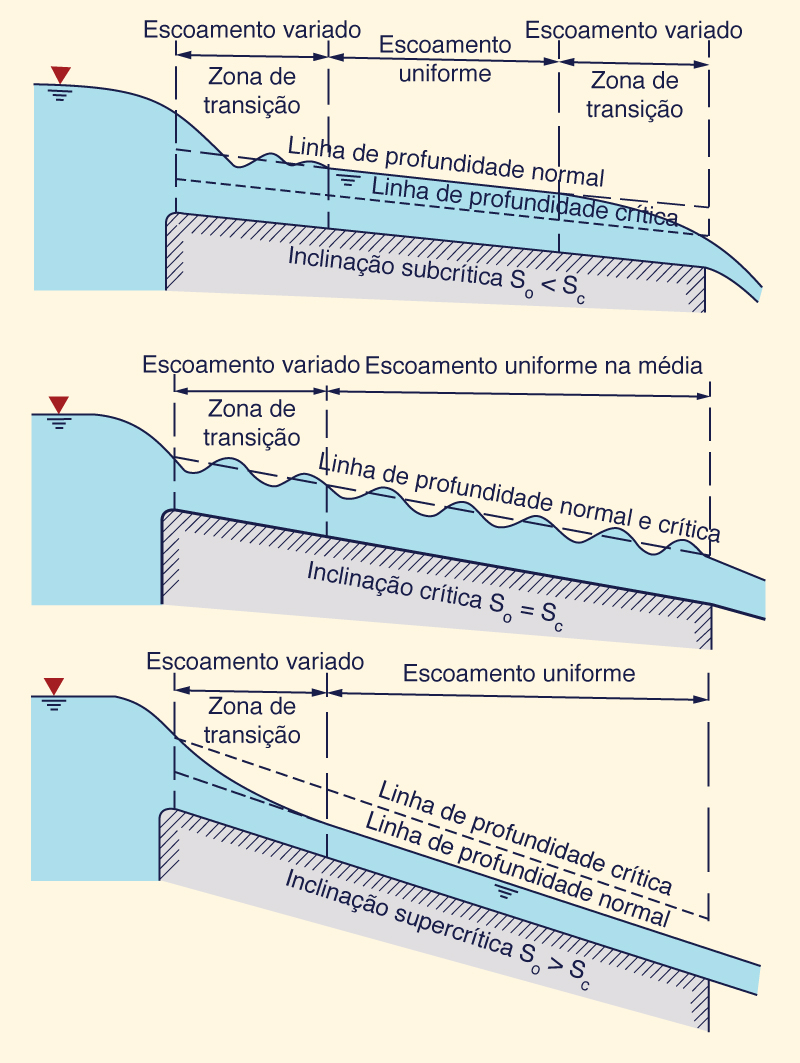
A profundidade do fluxo uniforme � conhecida como profundidade normal. A Figura 5-1 mostra o estabelecimento de fluxo uniforme em um canal suficientemente longo. A figura superior mostra o fluxo normal subcr�tico, com controles de se��o à montante e à jusante. A figura central mostra o fluxo cr�tico, com controles de se��o à montante e à jusante. A figura inferior mostra o fluxo normal supercr�tico, apenas com o controle da se��o à montante.
|
Velocidade do fluxo uniforme
Em geral, a velocidade m�dia do fluxo uniforme � descrita pela seguinte f�rmula:
V = C R x S y | (5-2) |
Em que: C = coeficiente de atrito;
R = raio hidr�ulico (sendo R = A/P, onde A = área molhada e P = perímetro molhado);
x e y = expoentes em função da rugosidade e da forma da se��o do canal.
Os expoentes x e y variam de acordo com o tipo de rugosidade (laminar, turbulenta, transit�ria ou laminar-turbulenta mista) e com o formato da se��o transversal (arbitr�ria, hidraulicamente ampla, retangular, trapezoidal, triangular ou inerentemente est�vel).
Na pr�tica, existem duas f�rmulas uniformes de fluxo estabelecidas: (1) a f�rmula de Ch�zy e (2) a f�rmula de Manning. Algumas varia��es dessas f�rmulas s�o atuamente utilizadas, dentre elas a fórmula adimensional de Ch�zy e a de Manning-Strickler.
5.2 F�RMULA DE CHÉZY
Para derivar a f�rmula de Ch�zy, a tens�o de cisalhamento τb desenvolvida ao longo do fundo do canal � modelada como uma lei de atrito quadr�tico:
τb = ρ f V 2 | (5-3) |
Em que: ρ = densidade de massa;
f = coeficiente de atrito;
V = velocidade m�dia.
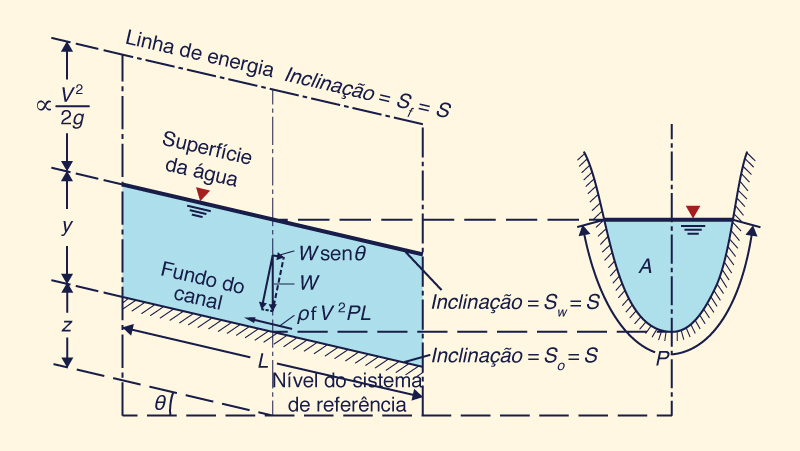
Esta equa��o � adimensional. Dessa forma, ela tem uma base te�rica consolidada. A for�a de cisalhamento τb desenvolvida ao longo do per�metro molhado P de um volume de controle de comprimento L � (Fig. 5-2):
Fs = τb PL = ρ f V 2 PL | (5-4) |
|
O peso da �gua no volume de controle � W. Essa for�a gravitacional está na dire��o do movimento de forma que:
Fg = W sen θ | (5-5) |
Para um canal de pequena declividade: sein θ ≅ tan θ = S. Portanto:
Fg = W tan θ = W S = γ A L S | (5-6) |
Igualando as for�as de atrito (Eq. 5-4) e as gravitacionais (Eq. 5-6):
ρ f V 2 P = γ A S | (5-7) |
Que se reduz a:
f V 2 = g (A /P ) S = g R S | (5-8) |
Em que: R = raio hidráulico.
Resolvendo V:
V = (g/f )1/2 (R S ) 1/2
(5-9)
V = C (R S )1/2
(5-10)
Em que: C = coeficiente de Ch�zy.
O coeficiente de Ch�zy é definido da seguinte forma:
C = (g/f )1/2 | (5-11) |
Assim, o fator de atrito f na Eq. 5-3 �:
g | (5-12) |
A Eq. 5-10 corresponde à f�rmula de Ch�zy. Uma varia��o da f�rmula de Ch�zy pode ser obtida resolvendo-se a declividade inferior S da Eq. 5-8:
V 2 | (5-13) |
A qual � equivalente a:
D V 2 | (5-14) |
Dada a Eq. 4-6, a Eq. 5-14 é reduzida para:
D | (5-15) |
A Eq. 5-15 � basicamente a mesma da Eq. 4-5, que foi derivada da equa��o de Darcy-Weisbach aplicada ao fluxo em canal aberto. Assim, a equa��o adimensinal de Ch�zy (Eq. 5-15) e a equa��o modificada de Darcy-Weisbach (Eq. 4-5) s�o as mesmas.
Para um canal hidraulicamente amplo, D ≅ R,a Eq. 5-15 se reduz à:
|
S = f F 2 | (5-16) |
Que � o mesmo que a Eq. 4-8.
A Tabela 5-1 mostra os valores correspondentes de f, fator de atrito de Darcy-Weisbach f e coeficientes de Ch�zy.
| [Veja tambén o video do laboratório: Escoamento uniforme]. |
| ||||||||||||||||||||||||||
| ||||
|
Antoine Ch�zy nasceu em Chalon-sur-Marne, Fran�a, em 1 de setembro de 1718 e morreu em 4 de outubro de 1798. Em 1749, trabalhando em Amsterd�, Cornelius Velsen afirmou:
"A velocidade deve ser proporcional � raiz quadrada da inclina��o." Em 1757, em Hannover, Alemanha, Albert Brahms escreveu:
Velsen e Brahms estavam trabalhando nas leis e teorias gerais de Torricelli e Bernoulli. Ch�zy usou algumas dessas id�ias para desenvolver sua f�rmula.
Foi dada a Ch�zy a tarefa de determinar a se��o transversal e a vazão relacionada para um canal proposto no rio Yvette, que fica perto de Paris, mas em uma altitude mais alta.
Em 1776, Ch�zy escreveu outro artigo, intitulado: "F�rmula para encontrar a velocidade uniforme que a �gua ter� em uma vala ou em um canal do qual a inclina��o � conhecida". V = 272 (ah/p)1/2 Em que: h � a declividade, a � a �rea e p � o per�metro molhado. O coeficiente 272 � dado para o canal de Courpalet em um antigo sistema de unidades. No sistema m�trico, o valor equivalente �: V = 31 (ah/p)1/2 Para o rio Sena, o valor do coeficiente � 44. Clemens traduziu para o ingl�s os dois artigos de Ch�zy. Riche de Prony, um dos ex-alunos de Ch�zy, foi o primeiro a usar a f�rmula de Ch�zy. Mais tarde, em 1801, na Alemanha, Eytelwein usou as id�ias de Ch�zy e De Prony para promover o desenvolvimento da f�rmula. |
5.3 F�RMULA DE MANNING
A f�rmula de Manning, em unidades SI, �:
| 1 V = ____ R 2/3 S 1/2 n | (5-17) |
Em que: n = coeficiente de atrito de Manning, fator de atrito ou simplesmente n de Manning.
Nas unidades habituais dos EUA, a f�rmula de Manning �:
1,486 | (5-18) |
A quantidade 1,486 � um fator de convers�o resultante da equival�ncia (3,28 pés/m)1/3 = 1.48582 ≅ 1.486. O fator � necess�rio para expressar a equa��o original de Manning (Eq. 5-17) em unidades habituais nos EUA.
Para comparar com a f�rmula de Ch�zy, a equa��o de Manning � expressa da seguinte forma:
1,486 | (5-19) |
Comparando as Eqs. 5-10 e 5-19, obem-se a rela��o entre os coeficientes de Manning e Ch�zy:
1,486 | (5-20) |
A equa��o 5-20 implica que, enquanto C varia com o raio hidr�ulico, o valor de n n�o varia. Isso pode acontecer praticamente em canais prism�ticos (artificiais), mas geralmente n�o ocorre em canais naturais (Barnes, 1967).
Nos canais naturais, o valor de n pode variar com o est�gio e a profundidade do fluxo. Isso � atribu�do a:
Varia��es naturais na rugosidade do canal com o aumento do est�gio, incluindo o efeito dos fluxos de extravazamento (Fig. 2-15 na Seção 2.2), ou
Altera��es morfol�gicas no atrito total do fundo, composto pelo atrito da pele e da forma, � medida que o fluxo sobe do est�gio baixo, passando pelo est�gio intermedi�rio, at� o est�gio alto (Simons e Richardson, 1966).
F�rmulas emp�ricas para o n de Manning
Diversas correla��es entre n de Manning e tamanho de part�cula (di�metro do gr�o) foram desenvolvidas. Williamson (1951) correlacionou o fator de atrito de Darcy-Weisbach f com a rugosidade relativa para produzir a seguinte rela��o (Henderson, 1966):
| ks | (5-21) |
Em que: ks = rugosidade do gr�o, em unidades de comprimento;
R = raio hidr�ulico.
Como f = 8 (g /C 2), a Eq. 5-21 se reduz para:
8g R | (5-22) |
Nas unidades habituais dos EUA, a Eq. 5-22 pode ser convenientemente reduzido para:
1,486 R1/6 | (5-23) |
Comparando a Eq. 5-23 com a Eq. 5-20, n pode ser expresso em termos de rugosidade dos limites da seguinte forma (ks em p�s):
n = 0,0311 ks1/6 | (5-24) |
Uma express�o geral para n de Manning em termos de rugosidade relativa e rugosidade absoluta � (Chow, 1959):
n = [f (R/ks)] ks1/6 | (5-25) |
Isso implica que na Eq. 5-24 a rugosidade relativa � uma constante (0,0311).
Supondo que a rugosidade dos limites possa ser representada pelo tamanho de part�cula d84, ou seja, aquele para o qual 84% dos gr�os (em peso) s�o mais finos, a Eq. 5-24 converte para:
| n = 0,0311 d841/6 | (5-26) |
Strickler usou uma constante (0,0342) para a fun��o de rugosidade relativa f(R/ks) e o tamanho m�dio de part�cula d50 como o di�metro representativo do gr�o, para produzir:
| n = 0,0342 d501/6 | (5-27) |
Já que d84 > d50, as equa��es de Strickler e Williamson s�o consideradas mutuamente consistentes.
A Tabela 5-2 mostra os valores n de Manning calculados com a f�rmula Strickler (Eq. 5-27).
| ||||||||||||||
| ||||
|
Robert Manning nasceu na Normandia, Fran�a, em 1816, e morreu em 1897. Em 1826, mudou-se para Waterford, na Irlanda, e trabalhou como contador. Em 1846, durante o ano da grande fome, Manning foi recrutado para a Divis�o de Drenagem Arterial do Gabinete Irland�s de Obras P�blicas. Depois de trabalhar como desenhista por um tempo, foi promovido a engenheiro assistente. Em 1848, tornou-se engenheiro distrital, cargo que ocupou at� 1855. Como engenheiro distrital, leu "Trait� d'Hydraulique" de d'Aubisson des Voissons, ap�s o qual desenvolveu um grande interesse em hidr�ulica. De 1855 a 1869, Manning foi contratado pelo Marqu�s de Downshire, enquanto supervisionava a constru��o do Dundrum Bay Harbor, na Irlanda, e projetou um sistema de abastecimento de �gua para Belfast. Ap�s a morte do marqu�s em 1869, Manning retornou ao Gabinete Irland�s de Obras P�blicas como assistente do engenheiro-chefe. Ele se tornou engenheiro-chefe em 1874, cargo que ocupou at� sua aposentadoria em 1891. Manning n�o recebeu nenhuma educa��o ou treinamento formal em mec�nica dos fluidos ou engenharia. Sua forma��o cont�bil e pragmatismo influenciaram o seu trabalho e o levaram a reduzir os problemas � sua forma mais simples. Ele comparou e avaliou sete f�rmulas mais conhecidas da �poca: Du Buat (1786), Eyelwein (1814), Weisbach (1845), St. Venant (1851), Neville (1860), Darcy e Bazin (1865) e Ganguillet e Kutter (1869). Em seguida, calculou a velocidade obtida de cada f�rmula para uma determinada declividade e para o raio hidr�ulico variando de 0,25 m a 30 m. Ent�o, para cada condi��o, ele encontrou o valor m�dio das sete velocidades e desenvolveu uma f�rmula que melhor se ajustou aos dados. A f�rmula original de melhor ajuste de Manning foi a seguinte: V = 32 [RS (1 + R1/3)]1/2 A qual, posteriormente, ele simplificou para: V = C Rx S1/2 Em 1885, Manning atribuiu a x o valor de 2/3 e escreveu sua f�rmula da seguinte maneira: V = C R2/3 S1/2 Em uma carta a Flamant, Manning afirmou: "O rec�proco de C corresponde intimamente ao de n , conforme determinado por Ganguillet e Kutter; ambos C e n s�o constantes para o mesmo canal". Em 4 de dezembro de 1889, aos 73 anos de idade, Manning prop�s a sua f�rmula � Institui��o de Engenheiros Civis da Irlanda. Essa f�rmula viu a luz em 1891, em um artigo escrito por ele intitulado "Sobre o fluxo de �gua em canais e tubula��es abertas", publicado nas Transactions of the Institution of Civil Engineers (Irlanda). Manning n�o gostou de sua pr�pria equa��o por dois motivos: primeiro, era dif�cil naqueles dias determinar a raiz c�bica de um n�mero e depois elev�-la ao quadrado utilizando a pot�ncia 2/3. Al�m disso, a equa��o estava dimensionalmente incorreta e, para obter a corre��o dimensional, ele desenvolveu a seguinte equa��o: V = C (gS)1/2 [R1/2 + (0,22/m1/2 )(R - 0.15 m)] Na qual = m = "altura de uma coluna de merc�rio que equilibra a atmosfera" e C = "n�mero adimensional que variava com a natureza da superf�cie". No entanto, nos livros did�ticos do final do s�culo XIX, a f�rmula de Manning foi escrita da seguinte maneira:
V = (1/n) R2/3 S1/2
Por meio do seu "Manual de Hidr�ulica", King (1918) levou à generalização da f�rmula de Manning, na forma como � conhecida hoje, bem como � aceita��o de que o coeficiente de Manning C deve ser o inverso do n de Kutter . Nos Estados Unidos, n � referido como coeficiente de atrito de Manning, ou simplesmente n de Manning. Na Europa, o Strickler K � o mesmo que o Cn de Manning , ou seja, o rec�proco de n. Quando K � usado no lugar de n, a equa��o de Manning � chamada de equa��o de Manning-Strickler ou Strickler. |
5.4 COEFICIENTE DE RUGOSIDADE DE MANNING
Dada a Eq. 5-17 (ou 5-18), uma vez conhecidas tr�s das vari�veis, a quarta pode ser calculada. Normalmente, R e S s�o conhecidos e n � estimado, a partir do qual V pode ser calculado. Este � o m�todo direto, a maneira mais t�pica de usar a equa��o de Manning.
Quando maior precis�o � necess�ria, ou ent�o, quando n n�o pode ser estimado com total certeza, recomenda-se uma medi��o da velocidade V , juntamente com a medi��o do raio hidr�ulico R e da inclina��o do canal Sn , para calcular n . Este procedimento � chamado de m�todo inverso ou m�todo de calibra��o. Na pr�tica, a maioria dos aplicativos usou o m�todo direto.
Estimativa do coeficiente n de Manning
N�o existe m�todo ou procedimento exato para estimar o n de Manning . Um conjunto comprovado de recomenda��es � dado abaixo.
Recomenda��es para a estimativa do coeficiente n de Manning
|
Chow (1959) apresentou uma cole��o pict�rica de vinte e quatro (24) canais t�picos para os quais o n de Manning foi estabelecido. Os valores documentados por Chow variam de n = 0,012 (um canal revestido com lajes de concreto, com superf�cie muito lisa) at� n = 0,150 (um rio natural em solo argiloso, inclina��es laterais irregulares e fundo irregular). Chow (1959) listou valores do coeficiente de Manning t�o baixo quanto n = 0,008 (lucite, pl�stico acr�lico) at� t�o alto quanto n = 0,200 (plan�cies de inunda��o de c�rregos naturais, com salgueiros densos, no ver�o) (Tabela 5-4). Esses valores s�o aplic�veis escoamento de canais no regime turbulento.
Barnes (1967) apresentou uma cole��o pict�rica colorida de cinquenta (50) canais de fluxo t�picos nos Estados Unidos, para os quais o n de Manning havia sido calculado por calibra��o. A cole��o Barnes pode ser visualizada online em Caracter�sticas de rugosidade dos canais naturais. O valor mais baixo de n de Manning documentado por Barnes � n = 0,024, para o rio Columbia em Vernita, Washington (Fig. 5-3). O valor mais alto de n de Manning � n = 0,075, para Rock Creek, perto de Darby, Montana (Fig. 5-4).
|
|
Arcement e Schneider (1989) apresentaram uma cole��o pict�rica colorida de quinze (15) plan�cies de inunda��o t�picas no sudeste dos Estados Unidos, para as quais o n de Manning foi calculado por calibra��o. A cole��o Arcement e Schneider pode ser visualizada online nos Coeficientes de rugosidade de Manning para canais naturais e plan�cies de inunda��o. O valor mais baixo de n de Manning, documentado por Arcement e Schneider, � n = 0,100, correspondendo a Cypress Creek, perto de Downsville, Louisiana (Fig. 5-5). O valor mais alto � n = 0,200, correspondendo a Thompson Creek, perto de Clara, Mississippi (Fig. 5-6).
|
|
Na pr�tica, o valor de n de Manning � altamente vari�vel. Nos canais naturais dos rios, pode variar de um pouco mais baixo que 0,020 para alguns rios muito grandes, com um limite relativamente suave (Fig. 5-7), e mais alto que 0,200 para pequenos riachos em c�rregos �ngremes nas montanhas
|
|
| |||||||||||||||||||||||||||||||||
Cowan (1956) desenvolveu uma metodologia racional para estimar o n de Manning. A equa��o de Cowan �:
| n = (no + n1 + n2 + n3 + n4 ) m5 | (5-28) |
Em que:
no = valor básico de n para um canal reto, uniforme e declividade suave;
n1 = valor adicional para compensar irregularidades na superf�cie;
n2 = valor adicional considerando as varia��es no tamanho e formato da se��o transversal;
n3 = valor adicional para a compensação das obstru��es;
n4 = valor adicional para para a compensação do efeito da vegeta��o nas condi��es de escoamento;
m5 = fator relacionado à sinuosidade do canal (meandros).
A Tabela 5-3 lista os valores apropriados a serem usados na Eq. 5-28.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
A Tabela 5-4 lista os valores de n de Manning para canais de v�rios tipos, compilados por Chow (1959). Para cada tipo de canal, os valores m�nimo, normal e m�ximo de n s�o mostrados. Os valores normais s�o recomendados apenas para canais com boa manuten��o. Os valores geralmente recomendados para o projeto s�o mostrados em negrito.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Clicar -aqui- para obter a Tabela 5-4 completa. |
5.5 DETERMINA�O DO ESCOAMENTO UNIFORME
Da Eq. 5-2, a vazão no fluxo de canal aberto �:
Q = V A = C R x S y A | (5-29) |
A equa��o 5-29 pode ser expressa da seguinte maneira:
Q = K S y = K S 1/2 | (5-30) |
Em que: K = transporte, definido como:
K = C R x A | (5-31) |
Ou, alternativamente:
Q | (5-32) |
De acordo com Ch�zy:
K = C A R 1/2 | (5-33) |
Segundo Manning, em unidades do SI:
1 | (5-34) |
Nas unidades habituais dos EUA:
1,486 | (5-35) |
O transporte K cont�m informa��es sobre atrito, tamanho e forma da se��o transversal e � independente da inclina��o do canal.
Canais com rugosidade composta
Um canal que transborda geralmente possui mais de um valor de n de Manning, um para a parte interna do escoamento e dois adicionais, um para a margem esquerda e outro para a direita (Fig. 5-9). Um valor composto de n de Manning pode ser calculado sob a suposi��o de que as velocidades para as tr�s subse��es (interna, margem esquerda e direita) permanecem as mesmas. Embora essa suposi��o seja conveniente, ela evita a poss�vel n�o uniformidade de fluxo na se��o transversal composta.
Considere um canal de rugosidade vari�vel ao longo do seu per�metro �mido, com N sendo o n�mero de subse��es. Os per�metros molhados s�o: P1, P2, P3, ..., PN. Supondo que todas as velocidades são iguais:
V1 = V2 = V3 = VN = V | (5-36) |
Para qualquer subse��o i :
1 | (5-37) |
1 | (5-38) |
A �rea de fluxo da subse��o i �:
Vi 3/2 ni 3/2 Pi | (5-39) |
A �rea total de fluxo do canal �:
V 3/2 n 3/2 P | (5-40) |
A �rea total do fluxo � igual � soma das sub�reas. Portanto:
| (5-41) |
| N |
Da Eq. 5-36, todas as velocidades s�o iguais. Assim, a Eq. 5-41 reduz para:
| (5-42) |
| N |
Assim, o valor de n de Manning para um canal de se��o transversal composta �:
| ∑ (ni 3/2 Pi ) N n = [ _________________ ] 2/3 P | (5-43) |
|
A se��o transversal de um canal pode ser composta por v�rias subse��es distintas, e cada uma delas pode ter uma rugosidade diferente. Por exemplo, um canal aluvial sujeito a inunda��es sazonais geralmente consiste em um canal principal e dois canais laterais (Fig. 5-9). Os canais laterais s�o geralmente mais �speros que o canal principal; portanto, a velocidade m�dia no canal principal � geralmente maior que a dos canais laterais. A equa��o de Manning pode ser aplicada separadamente a cada subse��o e a vazão total � igual � soma das vazãos da subse��o. Para o canal como um todo, a velocidade m�dia � igual � vazão total dividida pela �rea total.
O coeficiente de distribui��o de velocidade aplic�vel a todo o canal � diferente dos coeficientes de distribui��o de velocidade aplic�veis a cada subse��o. O coeficiente de distribui��o de velocidade total pode ser calculado como explicado abaixo.
Suponha um n�mero total de subsec��es N e v�rias subsec��es i que variam de 1 a N.
Qi = Vi Ai | (5-44) |
Em que: Qi = vazão atrav�s subsec��o i;
Vi = velocidade m�dia atrav�s subse��o i na �rea de fluxo Ai.
Al�m disso, da Eq. 5-30:
Qi = Ki S 1/2 | (5-45) |
Em que: Ki = transporte atrav�s subse��o i (Eq. 5-33 ou 5-34).
Combinando as Eqs. 5-44 e 5-45:
Vi = (Ki / Ai) S 1/2 | (5-46) |
A vazão total �:
N
| (5-47) |
Usando a Eq. 5-45 na Eq. 5-47:
N
| (5-48) |
Da Eq. 2-4, Q = V A. Portanto:
N
| (5-49) |
Da Eq. 2-24, o coeficiente de energia � reafirmado da seguinte forma:
|
N Σ Vi 3 Ai i = 1 α = _____________ V 3A
| (5-50) |
Da mesma forma, da Eq. 2-31, o coeficiente de momento �:
N
| (5-51) |
Substituindo as Eqs. 5-46 e 5-49 em 5-50, o coeficiente de energia composto α, aplic�vel a toda a se��o transversal, � obtido:
N
| (5-52) |
Da mesma forma, substituindo as Eqs. 5-46 e 5-49 em 5-51, o valor composto de β �:
N A [ Σ (βi Ki 2 / Ai ) ] i = 1 β = ____________________________ N ( Σ Ki ) 2 i = 1
| (5-53) |
Exemplo 5-1.
|
C�lculo do fluxo uniforme
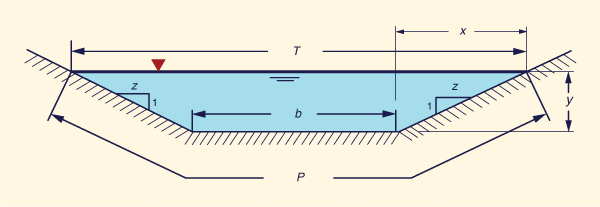
Com refer�ncia � Fig. 5-10, a seguinte propor��o � v�lida: z /1 = x /y. Ent�o, a largura do topo T �:
|
T = b + 2x = b + 2zy | (5-54) |
A �rea de fluxo A �:
A = (b + x ) y = (b + zy ) y | (5-55) |
|
O per�metro molhado P �:
|
P = b + 2 (y 2 + z 2y 2 )1/2 | (5-56) |
Simplificando:
|
P = b + 2 y ( 1 + z 2 )1/2 | (5-57) |
A partir da equa��o de Manning, a vazão Q �:
| k Q = _____ A R 2/3 S 1/2 n | (5-58) |
Em que: k = 1 em unidades SI e k = 1,486 em unidades habituais nos EUA.
Já que R = A /P, Eq. 5-58 se reduz para:
Q n A 5/3 | (5-59) |
Substituindo as Eqs. 5-55 e 5-57 na Eq. 5-59:
Q n [ (b + zy ) y ] 5/3 | (5-60) |
Simplificando:
| Q n Q n [ (b + zy ) y ] 5/2 - ( ________ ) 3/2 [ 2 y ( 1 + z 2 )1/2 ] - ( ________ ) 3/2 b = 0 k S 1/2 k S 1/2 | (5-61) |
Os dados de entrada que consistem em: (1) vazão Q , (2) largura inferior b, (3) inclina��o de tamanho z [z:H to 1:V, Fig. 5-10], (4) inclina��o inferior S, e (5) n de Manning. Com dados de entrada fornecidos, Eq. 5-61 � resolvido para a profundidade normal y. Ent�o, com Eqs. 5-54 e 5-55:
A | (5-62) |
Q | (5-63) |
A equa��o 5-61 � a f�rmula geral para fluxo uniforme ou normal, aplic�vel a canais prism�ticos de se��o transversal trapezoidal. Para um canal retangular: z = 0. Da mesma forma, para um canal triangular de se��o sim�trica: b = 0.
Para resolver a Eq. 5-61, � expresso da seguinte forma:
Q n Q n | (5-64) |
Fazendo a altera��o da vari�vel x = y para simplificar:
| Q n Q n f (x) = [ (b + zx ) x ] 5/2 - ( ________ ) 3/2 [ 2 x ( 1 + z 2 )1/2 ] - ( ________ ) 3/2 b k S 1/2 k S 1/2 | (5-65) |
A solu��o da Eq. 5-65 � realizada por um procedimento de tentativa e erro. Um algoritmo iterativo baseado no valor da fun��o � descrito abaixo. Um exemplo de fluxo normal � mostrado na Fig. 5-11.
Algoritmo de profundidade normal com base no valor da fun��o
|
|
Aproxima��o de Newton � raiz
A intera��o acima usa apenas o valor da fun��o para se aproximar da raiz. Um algoritmo mais r�pido utiliza a aproxima��o de Newton, que � baseada na tangente. Observe que, para que a itera��o de Newton funcione bem, � necess�rio primeiro se aproximar da raiz usando a itera��o de fun��o descrita acima. Caso contr�rio, o m�todo tangente de Newton pode n�o convergir.
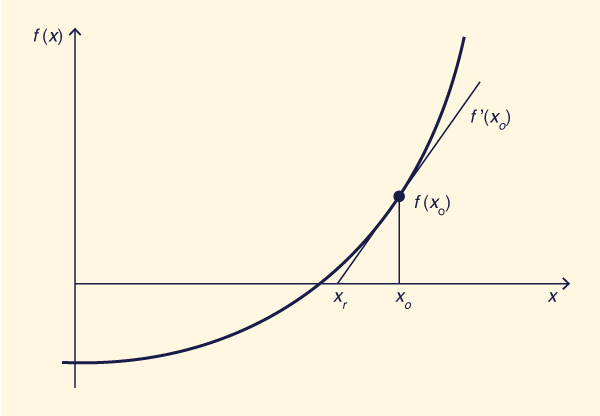
Com refer�ncia � Fig. 5-12, o valor da tangente em xo �:
f(xo) | (5-66) |
Em que: xo = valor de teste atual de x ;
f(xo) = valor da fun��o em xo ;
xr = novo valor de x, que se aproxima da raiz.
|
Da Eq. 5-66, resolvendo para xr :
f (xo) | (5-67) |
Como mostrado na Fig. 5-12, quando f (xo) aumenta com xo (como � o caso da Eq. 5-65), � medida que a raiz � passada, o valor da fun��o e o valor da tangente s�o positivos; portanto, o denominador da Eq. 5-66 tamb�m � positivo, e xr fica � esquerda de xo. A cada itera��o subsequente, a raiz � aproximada para valores ligeiramente superiores ou inferiores, at� que a toler�ncia especificada seja satisfeita.
� facilmente demonstrado que a Eq. 5-67 tamb�m se aplica quando f (xo) diminui � medida que xo aumenta, ou seja, como no caso de fluxo cr�tico, consulte a Se��o 4.2.
O valor de f '(x) �:
Q n |
| (5-68) |
Simplificando a Eq. 5-68:
Q n | (5-69) |
O procedimento para a aproxima��o de Newton da raiz da Eq. 5-65 � descrito abaixo.
Algoritmo de profundidade normal: aproxima��o de Newton
|
Exemplo 5-2.
|
Exemplo 5-3.
|
5.6 DETERMINA�O DA VAZ�O DE CHEIA
Os altos est�gios e as r�pidas correntes que prevalecem durante as inunda��es se combinam para aumentar o risco de acidentes e danos à população (Fig. 5-13). Portanto, geralmente n�o � poss�vel medir a vazão durante a passagem de uma inunda��o. Uma estimativa do pico de vazão pode ser obtida indiretamente pelo uso de f�rmulas de fluxo de canal aberto. Essa � a base do m�todo da �rea da inclina��o .
|
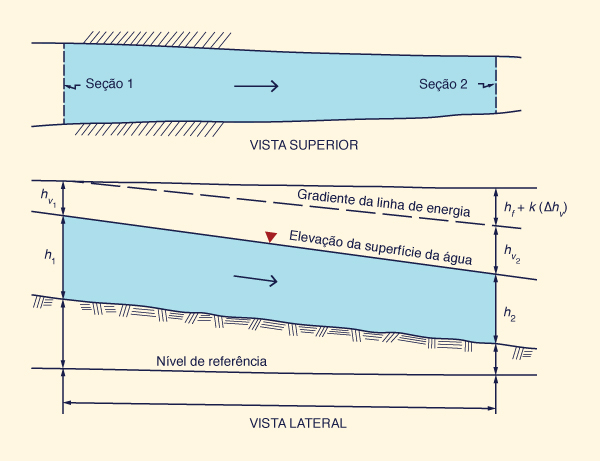
Para aplicar o m�todo da �rea da declividade para um determinado alcance do rio, s�o necess�rios os seguintes dados:
O comprimento do trecho;
A queda, ou seja, a mudan�a m�dia na eleva��o da superf�cie da �gua ao longo do trecho;
A �rea de fluxo, o per�metro molhado e os coeficientes da carga de velocidade nas se��es transversais à montante e � jusante;
O valor m�dio de n de Manning para o trecho.
As diretrizes a seguir s�o usadas na sele��o de um trecho adequado:
- As marcas d'�gua mais elevadas devem ser facilmente reconhec�veis (Fig. 5-14).
O trecho deve ser suficientemente longo para que a queda possa ser medida com precis�o.
A forma da se��o transversal e as dimens�es do canal devem ser relativamente constantes.
O trecho deve ser relativamente reto, embora um alcance de contra��o seja prefer�vel a um alcance em expans�o.
Pontes, curvas de canal, cachoeiras e outros recursos que causam n�o uniformidade de fluxo devem ser evitados.
|
A precis�o do m�todo da �rea da inclina��o melhora � medida que o comprimento do trecho aumenta (Fig. 5-15). Um trecho adequado deve atender a um ou mais dos seguintes crit�rios:
A rela��o entre o comprimento do alcance e a profundidade hidr�ulica deve ser superior a 75,
A queda deve ser maior ou igual a 0,15 m: F ≥ 0,15 m, e
A queda deve ser maior que qualquer uma das cargas de velocidade calculadas nas se��es transversais àa montante e à jusante.
|
O procedimento consiste nas seguintes etapas:
Calcule o transporte K nas se��es à montante e à jusante:
1
K1 = ( __ ) A1 R1 2/3
n
(5-70a) 1
K2 = ( __ ) A2 R2 2/3
n
(5-70b) Em que: K = transporte;
R = raio hidr�ulico;
n = valor m�dio de Manning n no trecho.Nas Eq. 5-70a e 5-70b, os índices 1 e 2 denotam as se��es à montante e à jusante, respectivamente. Ambas estão em unidades do SI.
Calcule a condu��o do trecho, igual � m�dia geom�trica dos transportes à montante e à jusante:
K = ( K1 K2 )1/2
(5-71) Em que: K = condu��o do trecho.
Calcule a primeira aproxima��o � inclina��o da energia:
F
S = ___
L
(5-72) Em que: S = primeira aproxima��o � inclina��o da energia;
F = queda;
L = comprimento do trecho.Calcule a primeira aproxima��o ao pico de vazão:
Qi = K S 1/2
(5-73) Em que: Qi = primeira aproxima��o para a vazão de pico.
Calcule as cargas de velocidade:
α1 ( Qi /A1 ) 2
hv1 = ______________
2g
(5-74a) α2 ( Qi /A2 ) 2
hv2 = ______________
2g
(5-74b) Em que: hv1 = carga de velocidade à montante;
hv2 = carga de velocidade à jusante;
α1 = coeficiente de carga de velocidade à montante;
α2 = coeficiente de carga de velocidade à jusante;
g = aceleração da gravidade.Calcule um valor atualizado da inclina��o da energia:
F + k ( hv1 - hv2 )
Si = ___________________
L
(5-75) Em que: Si = valor atualizado da inclina��o da energia;
k = coeficiente de perda.Para a expans�o do fluxo, ou seja, quando
A2 > A1, k = 0,5; para o contração do fluxo, ou seja, paraA1 > A2, k = 1.Calcule um valor atualizado do pico de vazão:
Qi = K Si 1/2
(5-76) -
Volte � Etapa 5 e repita as Etapas 5 a 7. O procedimento � encerrado quando a diferen�a entre dois valores sucessivos de pico de vazão Q obtidos na Etapa 7 � insignificante. Na pr�tica, isso geralmente � realizado com pelo menos duas itera��es.
Exemplo 5-4.
|
5.7 ESCOAMENTO SUPERFICIAL UNIFORME
O escoamento na planície de inundação de uma bacia � conhecido como fluxo superficial. Nesse caso, a profundidade do fluxo � normalmente muito pequena em compara��o com a largura. Sob essas condi��es, o fluxo pode ser laminar ou turbulento, dependendo da rugosidade absoluta e relativa. Se as velocidades e as profundidades do fluxo s�o suficientemente pequenas, o fluxo pode ser laminar; caso contr�rio, o fluxo pode ser transit�rio ou turbulento, dependendo do n�mero de Reynolds (Se��o 1.4).
No fluxo superficial, geralmente existe um regime laminar-turbulento misto. Esse tipo de fluxo � caracterizado por mudan�as do regime laminar para turbulento sob as condi��es de fluxo espacialmente variadas normalmente encontradas no fluxo superficial da bacia hidrogr�fica.
Fluxo de superf�cie laminar
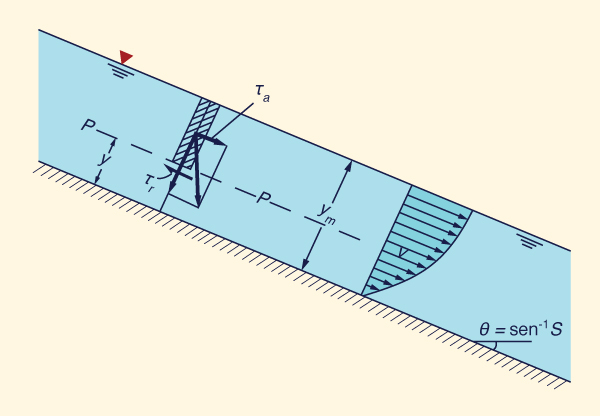
Com refer�ncia � Fig. 5-16, a tens�o de cisalhamento de atua��o no n�vel P �:
τa = γ (ym - y ) S | (5-77) |
De acordo com a lei de viscosidade de Newton, a tens�o de cisalhamento de resist�ncia em P � proporcional ao gradiente de velocidade vertical:
dv | (5-78) |
Em que: μ = constante de proporcionalidade referida como viscosidade din�mica.
|
Igualando as tens�es de a��o e resist�ncia:
dv | (5-79) |
Na forma diferencial:
|
μ dv = γ (ym - y ) S dy | (5-80) |
A densidade de massa γ = ρg e a viscosidade din�mica μ = ρν, na qual ν = viscosidade cinem�tica. Assim, a Eq. 5-80 se reduz para:
gS | (5-81) |
Integrando a Eq. 5-81:
gS | (5-82) |
gS y 2 v = _____ [ ym y - _____ ] + C ν 2
| (5-83) |
Em que: C = constante de integra��o.
Para v = 0, y = 0. Portanto, C = 0, e a rela��o velocidade-profundidade m�dia do fluxo �:
| gS y 2 v = _____ [ ym y - _____ ] ν 2
| (5-84) |
A Equa��o 5-84 revela que o perfil de velocidade do fluxo superficial uniforme tem uma distribui��o parab�lica.
A classifica��o de profundidade da vazão � obtida pela integra��o da Eq. 5-84 entre os limites de 0 e ym, ou seja, do fundo para a superf�cie, para produzir:
| gS y 2 q = ∫ v dy = _____ ∫ [ ym y - _____ ] dy ν 2
| (5-85) |
| gS ym 2 ym 3 q = _____ [ _____ - _____ ] ν 2 6
| (5-86) |
Que se reduz a:
| gS q = ______ ym 3 3ν
| (5-87) |
Ou:
q = CL ym 3 | (5-88) |
Em que: CL = coeficiente da taxa de vazão laminar, que é definido como:
| gS CL = ______ 3ν
| (5-89) |
Observe que, sob fluxo laminar, o expoente da classifica��o de vazão � β = 3 (Eq. 5-88), e a classifica��o � uma fun��o do atrito interno, ou viscosidade interna, representada pela viscosidade cinem�tica ν. Assim, o fluxo laminar � uma fun��o da temperatura.
Dada a Eq. 5-77, a velocidade m�dia no fluxo laminar, v = q /ym, �:
v = CL ym 2 | (5-90) |
A taxa de vazão turbulenta de Ch�zy �:
q = C S 1/2 ym 3/2
| (5-91) |
A taxa de vazão turbulenta de Manning em unidades do SI �:
q = (1/n) S 1/2 ym 5/3
| (5-92) |
Da mesma forma, em unidades habituais nos EUA �:
q = (1.486 / n) S 1/2 ym 5/3
| (5-93) |
Observa-se que o expoente da classifica��o varia de β = 3 para fluxo laminar (Eq. 5-88) a β = 3/2 para atrito turbulento de Ch�zy (Eq. 5-91) ou β = 5/3 para fric��o de tripula��o turbulenta (Eq. 5-92). No fluxo superficial uniforme, os valores de β na faixa entre laminar e turbulento representam a condi��o do fluxo laminar-turbulento misto (Se��o 1.3).
O n�mero de Vedernikov �:
(β - 1) v | (5-94) |
Sob V = 1, o fluxo � neutro e est�vel, promovendo o desenvolvimento de ondas de rolagem (Fig. 5-17). A rela��o entre o expoente β e o n�mero Vedernikov
Rela��o entre o expoente β e o n�mero de Vedernikov
|
Exemplo 5-5.
|
|
QUEST�ES
Quando o fluxo uniforme se torna inst�vel?
No que a f�rmula do Chezy se baseia?
Qual � a diferen�a entre as f�rmulas de Manning e Chezy?
Qual � o valor m�nimo do n de Manning que pode ser alcan�ado na pr�tica?
Qual � o intervalo de valores de n de Manning medido por Barnes?
Qual � o intervalo de valores de n de Manning medido por Arcement e Schneider para plan�cies de inunda��o?
Por que o c�lculo da rugosidade composta que usa a Eq. 5-43 é considerado apenas uma aproxima��o?
Quais s�o as cinco vari�veis de entrada usadas no c�lculo do fluxo uniforme em um canal trapezoidal?
Por que � melhor usar a aproxima��o de Newton para a raiz, ao invés de depender apenas da aproxima��o de fun��es para resolver o problema de profundidade normal?
Qual � a raz�o m�nima entre o comprimento do trecho e a profundidade hidr�ulica no m�todo da �rea de inclina��o?
Qual � o expoente da taxa de vazão/profundidade sob condi��es de fluxo laminar?
Qual � o expoente da taxa de vazão/profundidade sob o atrito turbulento do Chezy em canais hidraulicamente amplos?
Qual � o expoente da taxa de vazão/profundidade sob o atrito turbulento de Manning em canais hidraulicamente amplos?
Sob qual valor do n�mero de Froude � prov�vel que o fluxo se torne inst�vel sob condi��es de fluxo laminar?
PROBLEMAS
Prove que o fator de atrito de Darcy-Weisbach est� relacionado ao n de Manning pela seguinte rela��o:
fD = 8 g n 2 / (k 2 R 1/3)
Em que: fD = fator de atrito de Darcy-Weisbach, g = acelera��o da gravidade, R = raio hidráulico, e k = constante espec�fica para o sistema de unidades, igual a 1 em unidades SI e 1,486 em unidades habituais nos EUA. Expresse a rela��o em unidades habituais do SI e dos EUA.
Calcule a vazão Q usando a equa��o de Manning, dado que: �rea de fluxo A = 23,5 ft2; raio hidr�ulico R = 5,6 ft; inclina��o do canal S = 0,0025; Coeficiente de rugosidade de Manning
n = 0,035. Calcule a vaz�o Q usando a equa��o de Manning, dado que: �rea de fluxo A = 45 m2; raio hidr�ulico R = 6 m; inclina��o do canal S = 0,003; Coeficiente de rugosidade de Manning
n = 0,04. Dado f = 0,0025, calcule a vaz�o Q for uma �rea de fluxo A = 12,4 m2, raio hidr�ulico
R = 2,1 m; e inclina��o do canal S = 0,0015.Dado f = 0,0035, calcule a vaz�o Q for uma �rea de fluxo A = 18 pés2, raio hidr�ulico
R = 4,5 pés; e inclina��o do canal S = 0,0018.Use a caculadora CANAL EM LINHA 01 para calcular a profundidade normal, velocidade e n�mero de Froude para o seguinte caso: Q = 150 m3/s, b = 10 m, z = 2, So = 0,0005, n = 0,025.
Use a caculadora CANAL EM LINHA 01 para calcular a profundidade normal, velocidade e n�mero de Froude para o seguinte caso: Q = 250 cfs (pés cúbicos por segundo), b = 20 pés, z = 1, So = 0,001, n = 0,030.
Use a caculadora CANAL EM LINHA 15, para cacular a vazão do canal prismático com b = 20 p�s,
y = 3 p�s, z = 2, n = 0,025, S = 0,0016.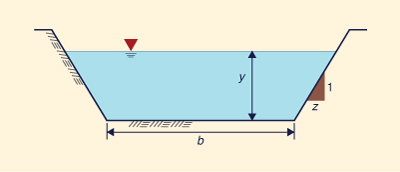
Fig. 5-18 Desenho esquemático do canal trapezoidal.
Use a caculadora CANAL EM LINHA 15, para cacular a vazão do canal prismático com b = 6 m,
y = 1 m, z = 1,5, n = 0,015, S = 0,0002.Uma inunda��o recente em Clearwater Creek deixou marcas de �gua observ�veis em um determinado trecho do rio. Para estimar a magnitude da inunda��o, os dados hidr�ulicos foram medidos em duas se��es transversais A e B, a uma dist�ncia de 1.850 p�s de dist�ncia. A queda do trecho entre as se��es transversais � de 9,1 p�s e o n m�dio de Manning � de 0,035. A �rea de fluxo à montante, o per�metro molhado e o coeficiente α de Coriolis s�o 550 p�s2, 55 p�s e 1,17; a �rea de fluxo à jusante, o per�metro molhado e o coeficiente α s�o 620 p�s2, 52 p�s e 1,10. Use a calculadora EM LINHA DECLIVE AREA da �rea de declive para calcular a vazão de inunda��o.
Calcule a vazão de largura unit�ria em um plano de fluxo terrestre, sob fluxo laminar, com profundidade m�dia de 1,5 cm e inclina��o de 0,001. Assuma a temperatura da �gua T = 20oC. Relate a vazão em L/s/m.
Usando o c�lculo diferencial, encontrar a profundidade relativa y/D em que a vazão � m�xima em um bueiro circular de di�metro D. Explique o motivo desse comportamento.
REFER�NCIAS
Arcement, G. J. e V. R. Schneider. 1989. Guide for selecting Manning's roughness coefficients for natural channels and flood plains. U.S. Geological Survey Water-Supply Paper 2339, Washington, D.C.
Barnes, H. A. 1967. Roughness characteristics of natural channels. U.S. Geological Survey Water-Supply Paper 1849, Washington, D.C.
Cowan, W. L. 1956. Estimating hydraulic roughness coefficients. Agricultural Engineering, Vol. 37, No. 7, pp. 473-475, July.
Chow, V. T. 1959. Open-channel hydraulics. McGraw-Hill, New York.
Henderson, M. H. 1966. Open-channel flow. Macmillan, New York.
Simons, D. B., e E. V. Richardson. 1966. Resistance to flow in alluvial channels. U.S. Geological Survey Professional Paper 422-J, Washington, D.C.
Williamson, J. 1951. The laws of flow in rough pipes. La Houille Blanche, Vol. 6, No. 5, September-October, p. 738.
| http://ponce.sdsu.edu/canais/index.html |
|
201102 06:35 |