|
|
|
CAPÍTULO 10: FLUJO NO PERMANENTE GRADUALMENTE VARIADO |
10.1 ECUACIONES DE GOBIERNO
|
|
Tres principios de conservación son aplicables en el flujo en canales abiertos:
-
Conservación de la masa, la cual puede ser: (a) permanente, o (b) no permanente,
-
Conservación de la energía, la cual es permanente (debido a que la energía es igual a la suma de todas las fuerzas, excluyendo la inercia, en el espacio, Ec. 2-15), y
-
Conservación de la cantidad de movimiento, que es no permanente (debido a que la cantidad de movimiento es igual a la suma de todas las fuerzas, incluyendo la inercia,
en el tiempo, Ec. 2-27).
El flujo permanente gradualmente variado combina las ecuaciones permanentes de conservación de la masa y la energía (Capítulo 7). El flujo no permanente gradualmente variado combina las ecuaciones no permanentes de la conservación de la masa y la cantidad de movimiento (Tabla 10-1). Por lo tanto, el flujo no permanente difiere del flujo permanente en su descripción de la variación temporal de las variables (descarga, nivel de la superficie del agua, profundidad de flujo, velocidad media, etc.).
En la práctica, el flujo permanente gradualmente variado se conoce simplemente como "flujo gradualmente variado" (FGV), mientras el flujo no permanente gradualmente variado se conoce comúnmente como "flujo no permanente" (FNP).
| Tabla 10-1 Leyes de conservación y tipos de flujo gradualmente variado. | |||
| Modelo | Primera ecuación: Conservación de la masa, ya sea → | Masa permanente | Masa no permanente |
| Segunda ecuación: Conservación de la → | Energía | Cantidad de movimiento | |
| Flujo | Tipo (nombre) → | Permanente FGV | No permanente FNP |
| Comúnmente conocido como → | Flujo gradualmente variado | Flujo no permanente | |
| Tratado en el → | Capítulo 7 | Capítulo 10 (este capítulo) | |
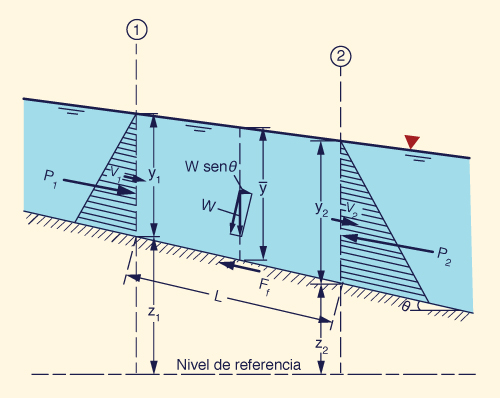
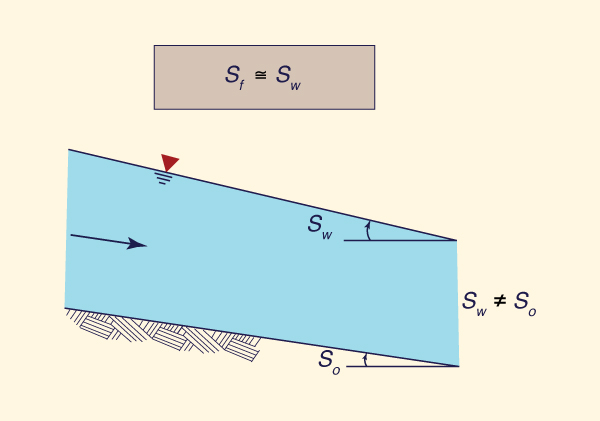
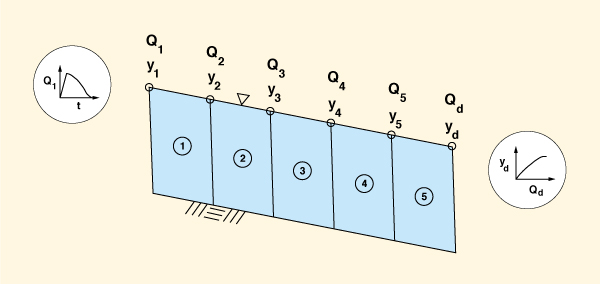
La Figura 10-1 muestra las fuerzas que actúan sobre un volumen de control comprendido
entre las secciones transversales 1 y 2.
Se muestran una fuerza del cuerpo y dos fuerzas de superficie.
La fuerza del cuerpo es el componente de la fuerza gravitacional
que actúa a lo largo de la dirección del movimiento
|
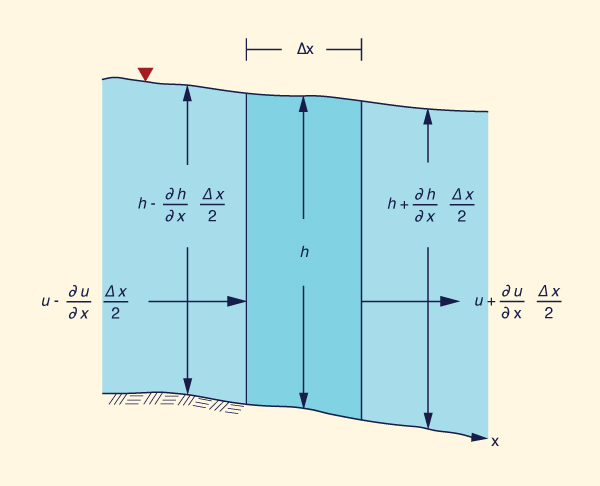
La derivación de las ecuaciones del flujo no permanente (flujo no permanente gradualmente variado) (Fig. 10-2) considera las leyes de conservación de la masa y cantidad de movimiento en un volumen de control (Fig. 10-3).
|
|
La conservación de la masa establece que:
|
Para un canal de ancho unitario (Liggett, 1975):
∂u Δx ∂h Δx ∂u Δx ∂h Δx ∂h | (10-1) |
Simplificando, y despreciando los términos de segundo orden, en cuanto Δx → 0:
∂h ∂h ∂u | (10-2) |
∂h ∂ | (10-3) |
La Ecuación 10-3 es la ecuación no permanente de conservación de la masa, comúnmente conocida como la ecuación de continuidad. Sin embargo, su nombre completo es: Ecuación diferencial de la continuidad del agua.
En el flujo permanente: ∂h/∂t = 0, y la Ec. 10-3 se reduce a: q = uh = constante. En general, para un canal de sección transversal A, la ecuación permanente de continuidad del agua es: Q = uA = constante.
La conservación de la cantidad de movimiento establece que:
|
La cantidad de movimiento, por unidad de ancho, es: ρ u (uh). Por lo tanto, la tasa neta de cantidad de movimiento que entra al volumen de control FΔ (fuerza por unidad de ancho) es:
∂ Δx ∂ Δx | (10-4) |
Las fuerzas que actúan sobre el volumen de control, a lo largo de la dirección del movimiento, son: (1) la fuerza de gravedad, (2) la fuerza debida al gradiente de presiones, y (3) la fuerza de fricción (Fig. 10-1).
La fuerza gravitacional, por unidad de ancho, es:
|
Fg = ρ g h Δx sin θ ≅ ρ g h Δx tan θ = ρ g h Δx So | (10-5) |
La fuerza debida al gradiente de presiones, por unidad de ancho, a lo largo de los lados del volumen de control, es:
h h 1 | (10-6) |
La fuerza de fricción a lo largo del fondo, por unidad de ancho, es similar a la fuerza de gravedad, pero de signo opuesto:
|
Ff = - ρ g h Δx Sf | (10-7) |
en la cual Sf = pendiente de fricción. [Como excepción, para canales con pendiente de fondo adversa, para los cuales So < 0, las fuerzas de gravedad y de fricción son del mismo signo].
El tamaño del volumen de control, por unidad de ancho, es:
∂ | (10-8) |
La conservación de la cantidad de movimiento es:
|
FΔ + Fg + Fp + Ff = Fm | (10-9) |
Sustituyendo las Ecs. 10-4 a 10-8 en la Ec. 10-9:
∂ Δx ∂ Δx |
|
1 ∂h 2 Δx ∂h 2 Δx + ____ ρ g [ (h 2 - _____ ____ ) - (h 2 + _____ ____ ) ] + ρ g h Δx Sf 2 ∂x 2 ∂x 2 |
∂ | (10-10) |
Simplificando:
∂ ∂ g ∂h 2 | (10-11) |
La Ecuación 10-11 está en forma de conservación. Para ciertas aplicaciones, debe permanecer en esta forma. Sin embargo, a menudo se expresa en forma reducida, operando en las derivadas:
∂u ∂h ∂ ∂u ∂h | (10-12) |
El segundo y tercer términos de la Ec. 10-12 tienen implícita la ecuación de continuidad (Ec. 10-3). Por lo tanto, la Ec. 10-12 se reduce a:
∂u ∂u ∂h | (10-13) |
Dividiendo por g, la Ec. 10-13 se expresa en unidades de pendiente:
1 ∂u u ∂u ∂h | (10-14) |
La Ecuación 10-14 se conoce como la ecuación de la cantidad de movimiento.
En términos de pendientes, se expresa de la siguiente forma:
|
Sa + Sc + Sp + Sf - So = 0 | (10-15) |
en la cual Sa = pendiente de aceleración local,
Sc = pendiente de aceleración convectiva,
Tipos de ondas
La Ecuación 10-15 indica que el balance de la cantidad de movimiento es un balance de pendientes. En el caso más general, cuando todas las fuerzas están presentes, todas las pendientes están actuando. Sin embargo, en ciertos casos, una o más pendientes pueden reducirse a cero, o pueden asumirse insignificantes, comparadas con las demás pendientes. Esta simplificación da lugar a varios tipos de ondas, los cuales se describen en la Tabla 10-2.
| Tabla 10-2 Tipos de ondas presentes en flujo no permanente en canales. | ||||||||
| No. | Tipo de onda | Pendientes | Nombre común | Aplicaciones | Sa
| Sc
| Sp
| Sf
| So
| 1
| Onda cinemática | sin difusión
|
|
| ✓
| ✓
| Onda cinemática
| Flujo superficial
| con difusión
|
| ✓
| ✓
| ✓
| Onda de difusión
| Tránsito de avenidas
| 3
| Onda dinámica
| ✓
| ✓
| ✓
|
|
| Onda de gravedad
| canales pequeños 4
| Onda dinámica | permanente
| ✓
| ✓
| ✓
| ✓
| Onda dinámica permanente
| Casos especiales
| 5
| Onda cinemática-dinámica mixta
| ✓
| ✓
| ✓
| ✓
| ✓
| Onda dinámica
| Tránsito de
avenida causada por | |
|
Aplicabilidad de los tipos de ondas
Las ondas cinemáticas [1] se aplican al flujo superficial, donde las pendientes de fondo son pronunciadas, típicamente mayores de So > 0.01. Las ondas de difusión [2] se aplican al tránsito de avenidas en arroyos y ríos, con pendientes de fondo intermedias (0.01 > So > 0.0001). Las ondas dinámicas [3] se aplican a ondas cortas de canaletas de laboratorio y pequeños canales. Las ondas dinámicas permanentes [4] se aplican a casos especiales en los cuales la eliminación de la aceleración local (Sa) se justifica por motivos prácticos. Sin embargo, es más correcto despreciar ambas Sa y Sc (es decir, una onda de difusión [2]), que sólo Sa (Ponce, 1990).
Las ondas cinemáticas-dinámicas mixtas [5] se aplican a las ondas que se producen en una rotura de presa, y también se pueden aplicar a los
canales de pendiente muy suave |
10.2 SOLUCIÓN LINEAR
|
|
Las ecuaciones 10-2 y 10-14, también conocidas como las ecuaciones
de Saint-Venant
∂h ∂h ∂u | (10-16) |
1 ∂u u ∂u ∂h | (10-17) |
Estas ecuaciones constituyen un conjunto de dos ecuaciones diferenciales parciales no lineares (en realidad, cuasi-lineares), que cuando se combinan adecuadamente resultan en una ecuación diferencial parcial de segundo orden de tipo hiperbólico, la cual posee dos soluciones. A la fecha, no existe una solución analítica completa del conjunto de Ecs. 10-16 y 10-17. Sin embargo, se puede obtener una solución aproximada linearizando las ecuaciones y utilizando el análisis de estabilidad linear (Ponce y Simons, 1977).
La pendiente de fricción Sf está directamente relacionada con el esfuerzo cortante de fondo τ por medio de la siguiente expresión (similar a la Ec. 6-16):
τ | (10-18) |
Como es de costumbre en los cálculos de estabilidad, las Ecs. 10-16 y 10-17 deben satisfacer el flujo no perturbado, en el cual u = uo , h = ho , y τ = τo. Además, deben satisfacer el flujo perturbado, en el cual u = uo + u' , h = ho + h' , y τ = τo + τ' . El superíndice ' representa una pequeña perturbación al flujo uniforme. Por lo tanto, todos los términos cuadráticos en los componentes de perturbación pueden ser despreciados, ya que son comparativamente muy pequeños.
La sustitución, después de linearización, de las variables perturbadas en las Ecs. 10-16, 10-17, y 10-18, resulta en lo siguiente (Lighthill y Whitham, 1955):
∂h' ∂h' ∂u' | (10-19) |
1 ∂u' uo ∂u' ∂h' τ' h' | (10-20) |
en las cuales:
τo | (10-21) |
El esfuerzo cortante de fondo τ se relaciona con la velocidad media u como sigue (Ec. 5-3):
|
τ = f ρ u 2 | (10-22) |
en la cual el factor de fricción f es (Ec. 5-12):
|
g | (10-23) |
Usando la Ec. 10-22, la Ec. 10-20 se modifica como sigue:
1 ∂u' uo ∂u' ∂h' u' h' | (10-24) |
Análisis de una perturbación pequeña
La solución para una perturbación pequeña en la profundidad de flujo se postula de la siguiente forma exponencial (Ponce y Simons, 1977):
h' | (10-25) |
en la cual el subíndice * representa variables adimensionales, e i = (-1)1/2. La cantidad σ* = número de onda adimensional, β* = factor de propagación complejo adimensional, y x* y t* son coordenadas adimensionales de espacio y tiempo, definidas como sigue:
2 π | (10-26) |
2 π Lo | (10-27) |
x | (10-28) |
uo | (10-29) |
y βI* es un factor de propagación de amplitud. La cantidad Lo es la longitud del canal en la cual el flujo uniforme cae (pierde) una carga igual a la profundidad:
ho | (10-30) |
Las perturbaciones de profundidad y velocidad se asocian con la siguiente relación:
u' | (10-31) |
La sustitución de las Ecs. 10-25 y 10-31 en las Ecs. 10-19 y 10-24 lleva al siguiente conjunto de ecuaciones algebraicas:
σ* u* + (σ* - β* ) d* = 0 | (10-32) |
[ 2 + i Fo2 (σ* - β* ) ] u* + (i σ* - 1 ) d* = 0 | (10-33) |
El cuadrado del número de Froude aparece en la Ec. 10-33:
|
uo 2 | (10-34) |
Las Ecuaciones 10-32 y 10-33 constituyen un sistema homogéneo de ecuaciones lineares en las incógnitas u* y h*. Para que la solución sea no trivial, el determinante de la matriz de coeficientes debe ser igual a cero. Esto lleva a la siguiente relación:
|
i β* 2 Fo2 - i σ* 2 (1 - Fo2 ) + 3 σ* - 2 β* - 2 i σ* β* Fo2 = 0 | (10-35) |
La Ecuación 10-35 es la ecuación característica que gobierna la propagación de ondas de amplitud pequeña. A través de una manipulación algebraica, la Ec. 10-35 se reduce a:
|
Fo2 β* 2 - 2 (σ* Fo2 - i ) β* - [ σ* 2 (1 - Fo2 ) + 3 σ* i ] = 0 | (10-36) |
La solución de la Ec. 10-36 es (Ponce y Simons, 1977):
1 | (10-37) |
en la cual
1 | (10-38) |
Las ecuaciones de celeridad adimensional y atenuación de las ondas primarias y secundarias son:
C + A | (10-39) |
B - E | (10-40) |
C + A | (10-41) |
B + E | (10-42) |
en las cuales:
1 | (10-43) |
|
B = ζ | (10-44) |
1 | (10-45) |
C + A | (10-46) |
C - A | (10-47) |
La celeridad relativa adimensional es:
C + A | (10-48) |
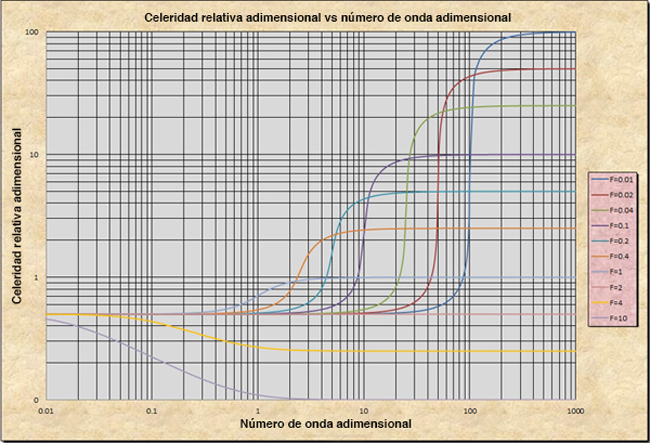
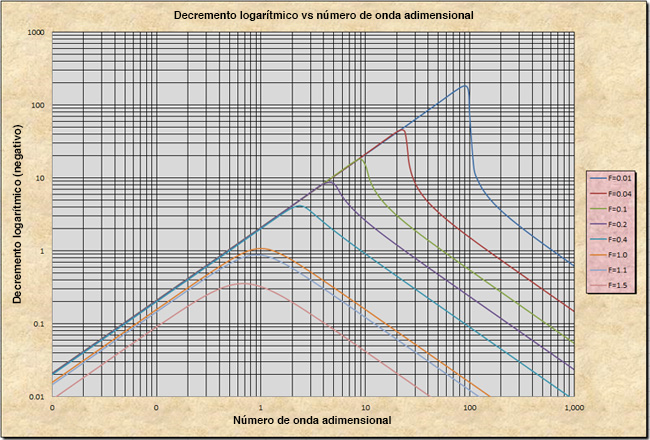
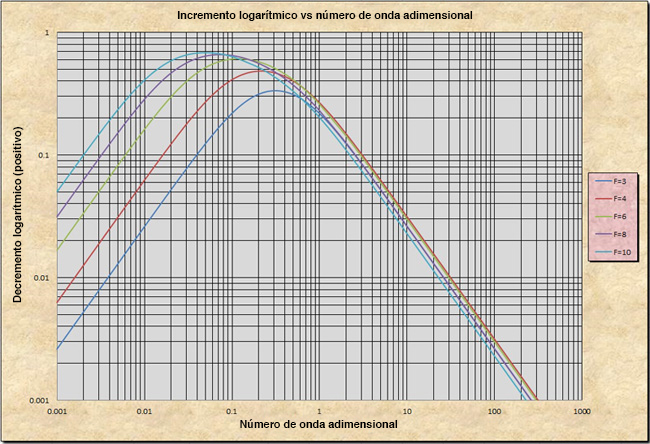
La Figura 10-4 muestra el gráfico de la celeridad relativa adimensional cr* en función del número de onda adimensional σ*. La Figura 10-5 muestra el gráfico del decremento logarítmico -δ1 en función del número de onda adimensional, σ*, aplicable para los números de Froude F < 2. La Figura 10-6 muestra el gráfico del incremento logarítmico de la onda +δ1 en función del número de onda adimensional σ*, aplicable para los números de Froude F > 2. De acuerdo a estos gráficos, las características de las ondas superficiales se describen en el recuadro siguiente.
|
|
|
Propagación de ondas superficiales en el flujo en canales 1
1 Ponce and Simons (1977) hacen un tratamiento detallado de la propagación de ondas superficiales en flujo en canales. |
10.3 ONDAS CINEMÁTICAS
|
|
Una onda cinemática es una idealización del flujo no permanente gradualmente variado que desprecia ambos términos de aceleración (local y convectiva) y el término de gradiente de presiones (Tabla 10-2). Ignorando dichos términos, la ecuación de cantidad de movimiento (Ec. 10.14) se reduce a la expresión de flujo uniforme:
|
Sf = So | (10-49) |
Sin embargo, la impermanencia del fenómeno se conserva a través del término que varía con el tiempo en la ecuación de continuidad (Ec. 10-3). La combinación de las Ecs. 10-3 y 10-49 da lugar a la ecuación de la onda cinemática.
Dado que q = uh, la Ec. 10-3 se puede expresar en términos de descarga por unidad de ancho:
∂h ∂q | (10-50) |
En términos de descarga Q, la ecuación de continuidad es:
∂A ∂Q | (10-51) |
El flujo uniforme (Ec. 10-49) puede ser representado mediante la relación descarga-área (curva de gasto):
|
Q = α A β | (10-52) |
en la cual α y β son el coeficiente y el exponente, respectivamente. El coeficiente α varía en función del tipo de fricción, la forma de la sección transversal, y la pendiente de fondo. El exponente β varía en función del tipo de fricción y la forma de la sección transversal.
Suponiendo que α y β son independientes de A, la Ec. 10-52 se representa como sigue:
dQ | (10-53) |
dQ Q | (10-54) |
dQ | (10-55) |
en la cual V = Q / A = velocidad media.
La ecuación de la onda cinemática se obtiene combinando las Ecs. 10-51 y 10-55:
∂Q ∂Q | (10-56) |
En términos de descarga por unidad de ancho q:
∂q ∂q | (10-57) |
La celeridad convectiva
La Ecuación 10-56 (o Ec. 10-57) es una ecuación diferencial parcial de primer orden. Esta ecuación describe la convección de la cantidad Q (o q) con la velocidad convectiva o celeridad ck, en la cual ck es:
|
ck = β V | (10-58) |
Dada la Ecuación 10-55, la velocidad convectiva también se puede expresar como sigue:
dQ | (10-59) |
Dado que dA = T dy (Ec. 3-11), en la cual T = ancho de la superficie, e y = elevación de la superficie del agua, la velocidad convectiva también puede ser expresada como sigue:
1 dQ | (10-60) |
La Ecuación 10-60 fue derivada originalmente por Kleitz (1877) y luego descubierta por Seddon (1900) a partir de observaciones de campo. A esta ecuación se le conoce como la Ley de Kleitz-Seddon, o simplemente Ley de Seddon. La Ecuación 10-58 se utiliza cuando β se conoce con certeza, la Ec. 10-59 en formulaciones teóricas, y la Ec. 10-60 en aplicaciones prácticas.
Dado que la Ec. 10-56 es una ecuación diferencial parcial de primer orden, no permite la difusión de la onda, es decir, la atenuación o disipación. La difusión sólo se puede obtener a través de un término de segundo orden. Suponiendo linearidad (una celeridad convectiva constante), una onda cinemática conveccionará su descarga con difusión nula; es decir, en la propagación, la descarga conservará su forma y permanecerá constante en el tiempo y en el espacio.
|
La ausencia de difusión
en una onda cinemática
La ausencia de difusión en una onda cinemática puede ser demostrada por medio de un tratamiento matemático. El diferencial total de Q es:
Por lo tanto:
La ecuación de onda cinemática es:
Comparando las Ecs. 10-56 y 10-62, se deduce que dQ/dt = 0, es decir, Q permanece constante en el tiempo para las ondas que viajan con la celeridad convectiva β V. |
El choque cinemático
Cuando la suposición de linearidad no se cumple, la onda cinemática
puede cambiar su forma, convirtiéndose en:
(a) más pronunciada o empinada [Fig. 10-7 (a)], o (b) más plana o atenuada
|
|
Cuando el aumento de pendiente procede sin control (es decir, sin límite), una onda cinemática se puede convertir en un choque cinemático. El choque cinemático es un fenómeno intrínsecamente relacionado con el concepto de la onda cinemática: Una onda debe ser cinemática antes de que pueda convertirse en un choque cinemático (Lighthill y Whitham, 1955). Kibler y Woolhiser (1970) explicaron la ocurrencia del choque cinemático de la siguiente manera:
|
El choque cinemático es real pero es poco común en el mundo físico, donde las irregularidades espaciales existentes se manifiestan como difusión, la cual contribuye a detener el desarrollo del choque. Por otra parte, es probable que el choque sea más común en el mundo computacional (digital), en el cual la regularidad espacial usualmente prescrita tiende a inhibir la difusión, promoviendo el desarrollo del choque cinemático "numérico."
La celeridad de la onda cinemáticaLa celeridad relativa de la onda cinemática, es decir, la celeridad de la onda cinemática relativa al flujo, es:
|
crk = (β - 1 ) V | (10-63) |
La celeridad relativa adimensional de la onda cinemática es:
crk | (10-64) |
De acuerdo con la Ec. 1-11, la celeridad relativa adimensional de la onda cinemática es:
V | (10-65) |
Por lo tanto, para V = 1, es decir, para el flujo neutralmente estable, el número de Froude es:
1 1 | (10-66) |
La Tabla 10-3 muestra la variación, con diversos tipos de fricción y sección transversal, de: (a) el exponente β, (b) la celeridad relativa adimensional de la onda cinemática cdrk, y (c) el número de Froude neutralmente estable.
| Tabla 10-3 Variación de β en función del tipo de fricción y sección transversal. | |||||
| [1] | [2] | [3] | [4] | [5] | [6] |
| β | Tipo de fricción | Tipo de sección transversal | cdrk | Fns | |
| 3 | 72 | Laminar | Hidráulicamente ancha | 2 | 1/2 |
| 8/3 | 64 | Laminar-turbulento mixto (25% Manning turbulento) | Hidráulicamente ancha | 5/3 | 3/5 |
| 21/8 | 63 | Laminar-turbulento mixto (25% Chezy turbulento) | Hidráulicamente ancha | 13/8 | 8/13 |
| 7/3 | 56 | Laminar-turbulento mixto (50% Manning turbulento) | Hidráulicamente ancha | 4/3 | 3/4 |
| 9/4 | 54 | Laminar-turbulento mixto (50% Chezy turbulento) | Hidráulicamente ancha | 5/4 | 4/5 |
| 2 | 48 | Laminar-turbulento mixto (75% Manning turbulento) | Hidráulicamente ancha | 1 | 1 |
| 15/8 | 45 | Laminar-turbulento mixto (75% Chezy turbulento) | Hidráulicamente ancha | 7/8 | 8/7 |
| 5/3 | 40 | Manning turbulento | Hidráulicamente ancha | 2/3 | 3/2 |
| 3/2 | 36 | Chezy turbulento | Hidráulicamente ancha | 1/2 | 2 |
| 4/3 | 32 | Manning turbulento | Triangular | 1/3 | 3 |
| 5/4 | 30 | Chezy turbulento | Triangular | 1/4 | 4 |
| 1 | 24 | Cualquiera | Inherentemente estable | 0 | ∞ |
La Tabla 10-3 permite concluir lo siguiente:
-
El valor del exponente β varía de β = 3 para el flujo laminar en un canal hidráulicamente ancho, a
β = 1 para un canal inherentemente estable. -
El valor de la celeridad relativa adimensional de la onda cinemática varía de
cdrk = 2 para el flujo laminar en un canal hidráulicamente ancho, a cdrk = 0 para un canal inherentemente estable. -
El número de Froude neutralmente estable varía de Fns = 0.5 para flujo laminar en un canal hidráulicamente ancho (es decir, el flujo superficial laminar), a Fns = ∞ para un canal inherentemente estable bajo cualquier tipo de fricción (aunque sea usualmente turbulento).
-
La celeridad relativa adimensional de la onda cinemática, aplicable para un canal hidráulicamente ancho bajo la fricción de Chezy, es
cdrk = 0.5, lo cual confirma los resultados mostrados en (el lado izquierdo de) la Fig. 10-5. Por lo tanto, las ondas cinemáticas tienen longitudes de onda L largas y correspondientemente números de onda adimensionales σ* pequeños. -
La celeridad relativa adimensional de la onda cinemática, aplicable para un canal hidráulicamente ancho bajo la fricción de Chezy, es
cdrk = 2/3; es decir, el valor de Manning supera al valor de Chezy en 1/6.
Nótese que el valor de β
puede ser inferior a 1 en
casos especiales, los cuales no se muestran en la Tabla 10-3;
por ejemplo, cuando la sección transversal no crece
monotónicamente con la profundidad,
como en el caso de flujo en una alcantarilla
circular. Además, dado que el número
de Froude tiene un límite superior
(correspondiente a la existencia de un
límite inferior en la fricción de fondo),
el valor Fns = ∞
no es práctico.
Suponiendo que el número de Froude máximo alcanzable es
En resumen, las ondas cinemáticas tienen las siguientes propiedades:
-
Las ondas cinemáticas viajan con una celeridad relativa adimensional igual a 0.5, para la fricción de Chezy. Para la fricción de Manning, el valor es 2/3.
-
Las ondas cinemáticas no se atenúan, pero pueden someterse a cambios de forma debido a fenómenos no lineares. En casos extremos en canales hidráulicamente anchos, la pendiente de la onda cinemática puede empinarse hasta el punto de convertirse en un choque cinemático.
|
Precauciones necesarias en la modelación de ondas cinemáticas 1
No obstante de que la teoría de la onda cinemática no considera la atenuación de la onda, ciertas soluciones numéricas de la Ec. 10-56 resultan en una atenuación perceptible y mensurable. Cunge (1969) explicó que esta contradicción se debe a que en las soluciones numéricas se produce un error, el cual se origina en el tamaño finito de la malla, manifiestándose como una difusión numérica. En cuanto más pequeña sea la malla, el efecto numérico será menor; sin embargo, todas las mallas numéricas son finitas, por lo tanto siempre habrá un error residual. El dilema se resuelve haciendo que la difusión numérica (es decir, matemática) simule la difusión física, si ésta última está presente. Este procedimiento es la base del método Muskingum-Cunge para el tránsito de avenidas, el cual se describe en la Sección 10.6. 1 Ponce (1991) contiene una explicación detallada de la controversia con respecto a las ondas cinemáticas. |
La onda cinemática se basa en una curva de gasto
(descarga-área) única,
Una onda cinemática es un tipo simplificado de onda, en el cual tres términos de la ecuación de cantidad de movimiento (Tabla 10-2) se desprecian debido a que son tan pequeños que son prácticamente nulos. Por lo tanto, la onda cinemática no es aplicable al caso general. Su uso se recomienda para cuando la impermanencia del flujo es despreciable. En la práctica, una onda cinemática se puede utilizar si se satisface la siguiente desigualdad adimensional (Ponce, 1989; Ponce, 2014):
tr
So Vo
| (10-67) |
en la cual tr = tiempo de subida del hidrograma,
So = pendiente de fondo,
Vo = velocidad media, y
10.4 ONDAS DIFUSIVAS
|
|
Una onda difusiva (u onda de difusión) es una idealización que desprecia ambos términos de aceleración de la ecuación de la cantidad de movimiento (Tabla 10-2). Por lo tanto la Ec. 10-14 se reduce a:
∂h | (10-68) |
Sin embargo, la impermanencia del fenómeno se conserva a través del témino de la ecuación de continuidad que varía en el tiempo (Ec. 10-3). La combinación de las Ecs. 10-3 y 10-68 da lugar a la ecuación de la onda difusiva.
La ecuación de la onda cinemática se derivó usando la ecuación del flujo permanente uniforme en vez de la ecuación de la cantidad de movimiento (Sección 10.4). Para derivar la ecuación de la onda difusiva, se utiliza el flujo permanente no uniforme (la pendiente de fricción es igual a la pendiente de la superficie del agua) (Fig. 10-8). En este caso, la curva de gasto usando la fórmula de Manning en unidades SI (Ec. 5-17) es:
1 dh | (10-69) |
en la cual el término entre paréntesis es la pendiente de la superficie del agua Sw.
Fig. 10-8 La suposición de la onda difusiva. |
La diferencia entre la onda cinemática y la onda difusiva está en el término de gradiente de presiones (dh/dx). Cuando se incluye este término, la ecuación resultante es de segundo orden y, por lo tanto, es capaz de simular la difusión. Lighthill y Whitham (1955) se refirieron a esta situación como la "difusión de las ondas cinemáticas," es decir, un tipo de onda cinemática que, aún sin incluír la inercia en su formulación, es capaz de atenuarse.
Para derivar la ecuación de la onda difusiva, la Ec. 10-51 se repite a continuación con pequeños cambios:
∂Q ∂A | (10-70) |
La Ecuación 10-69 se expresa en una forma más conveniente (Cunge, 1969):
dh | (10-71) |
en la cual m es el recíproco del cuadrado de la conducción K (Ec. 5-34):
1 | (5-34) |
Dado que dA = T dh, en la cual T = ancho de la superficie, la Ec. 10-71 se convierte en:
1 dA | (10-72) |
Las Ecuaciones 10-70 y 10-72 constituyen un conjunto de dos ecuaciones diferenciales parciales que describe las ondas difusivas. Estas ecuaciones se pueden combinar en una sola ecuación con Q como variable dependiente. Sin embargo, es necesario primero linearizar las ecuaciones alrededor de valores de referencia. Por simplicidad, se asume un ancho superior constante (por ejemplo, el caso de un canal hidráulicamente ancho).
La linearización de las Ecs. 10-70 y 10-72 se lleva a cabo
por medio de la teoría de perturbación pequeña
(Cunge, 1969).
Las variables Q, A, y m se pueden expresar en términos de la
suma de un valor de referencia (con subíndice o) y una
perturbación pequeña al valor de referencia
(con superíndice ' ):
∂Q' ∂A' | (10-73) |
1 ∂A' | (10-74) |
Diferenciando la Ec. 10-73 con respecto a x y la Ec. 10-74 con respecto a t:
∂2Q' ∂2A' | (10-75) |
1 ∂2A' ∂m' ∂Q' | (10-76) |
Utilizando la regla de la cadena y la Ec. 10-73 se obtiene:
∂m' ∂m' ∂A' ∂m' ∂Q' | (10-77) |
Combinando la Ec. 10-76 con la Ec. 10-77:
1 ∂2A' ∂m' ∂Q' ∂Q' | (10-78) |
Combinando las Ecs. 10-75 y 10-78 y reordenando términos, se obtiene:
∂Q' Qo ∂m' ∂Q' 1 ∂Q'2 | (10-79) |
Por definición: mQ 2 = Sf (Ec. 10-70). Por lo tanto:
∂Q' ∂Q Qo | (10-80) |
y de igual manera:
So | (10-81) |
Sustituyendo las Ecs. 10-80 y 10-81 en la Ec. 10-79, utilizando la regla de la cadena, y eliminando los superíndices, se obtiene la siguiente ecuación:
∂Q ∂Q ∂Q Qo ∂2Q | (10-82) |
El lado izquierdo de la Ec. 10-82 se conoce como la ecuación
de la onda cinemática, en la cual
∂Q/∂A es la celeridad de la onda.
El lado derecho es un término de segundo orden (en las derivadas parciales)
que representa el efecto de difusión física.
El coeficiente del término
de segundo orden tiene las dimensiones de difusividad
La difusividad hidráulica, una característica del flujo y del canal, se define como sigue:
Qo qo | (10-83) |
en la cual qo = Qo /T es la descarga de referencia por unidad de ancho. De la Ec. 10-83, se deduce que la difusividad hidráulica es pequeña para pendientes de fondo pronunciadas (por ejemplo, en los arroyos de montaña), y grandes para pendientes de fondo suaves (por ejemplo, en ríos de gran tamaño, cerca de su desembocadura al océano).
La Ecuación 10-82 describe el movimiento de las ondas de avenida de una
mejor manera que la
La Ecuación 10-82 es una ecuación diferencial parcial parabólica de segundo orden. Esta ecuación se puede resolver analíticamente, lo que lleva a la solución de analogía de difusión para las ondas de avenida (Hayami, 1951), o numéricamente con la ayuda de un esquema para ecuaciones parabólicas. Alternativamente, se puede igualar la difusividad hidráulica (Ec. 10-83) con el coeficiente de difusión numérica del método Muskingum (Sección 10.5). Este tipo de solución es la base del método Muskingum-Cunge (Sección 10.6).
La curva de gasto de la onda difusivaContrariamente a las ondas cinemáticas, las ondas difusivas no se basan en curvas de gasto de un sólo valor. En otras palabras, la curva de gasto de la onda difusiva contiene un ciclo de histéresis. Sin embargo, por lo general, la histéresis es tan pequeña que puede ser ignorada en la práctica. La curva de gasto cinemática se puede utilizar como una aproximación a la curva de gasto difusiva.
La celeridad de la onda difusivaDe acuerdo con la Ec. 10-82, la celeridad de la onda difusiva debe ser la misma que la celeridad de la onda cinemática (Ponce y Simons, 1977). Sin embargo, las ondas difusivas se atenúan; por lo tanto, la curva de gasto no tiene un solo valor. En la práctica, la celeridad de la onda difusiva es aproximadamente igual a la celeridad de la onda cinemática.
Aplicabilidad de las ondas difusivasUna onda difusiva es un tipo simplificado de onda en el cual dos términos de la ecuación de cantidad de movimiento (Tabla 10-2) son despreciables o muy pequeños. Si bien la onda difusiva se aplica para una gama más amplia de casos que la onda cinemática, aún no puede ser aplicada al caso general. Su uso se recomienda donde la impermanencia del flujo es de pequeña a mediana (las ondas se mantienen dentro del 30% de su fuerza original, medidas en un período de propagación). Una onda difusiva es aplicable en cuanto se satisfaga la siguiente desigualdad adimensimensional (Ponce, 1989; Ponce, 2014):
g
| (10-84) |
en la cual tr = tiempo de subida del hidrograma, So = pendiente de fondo, g = aceleración de la gravedad, y do = profundidad media del flujo.
Las ondas difusivas se aplican a la propagación de ondas de avenida (véase la analogía de difusión de Hayami en el recuadro siguiente). Mientras que las ondas cinemáticas se aplican a las ondas de avenida que no se atenúan, las ondas difusivas se aplican a las ondas de avenida que tienen una atenuación apreciable. Cuando la onda difusiva no toma en cuenta la propagación total exacta, solamente la onda cinemática-dinámica mixta (Véase "onda dinámica" en la Tabla 10-2) es capaz de resolver el problema correctamente. Sin embargo, en la práctica, las ondas difusivas se aplican a una amplia gama de problemas de ondas de avenida.
|
La analogía de difusión de ondas de avenida
En 1951, Hayami publicó un artículo titulado "Sobre la propagación de ondas de avenida," en el cual argumentó que las ondas de avenida podrían ser modeladas con una ecuación de convección-difusión similar a la Ec. 10-82. Hayami explicó el tema de la siguiente manera:
|
La difusividad hidráulica dinámica
La difusividad hidráulica (Ec. 10-83) es la propiedad fundamental de la onda difusiva. La difusividad hidráulica (o coeficiente de difusión) es directamente proporcional a la descarga por unidad de ancho e inversamente proporcional a la pendiente de fondo. Esta conclusión se aplica a las ondas difusivas, las cuales se rigen por la ecuación de convección-difusión representada por la Ec. 10-82.
Basándose en conceptos de teoría linear, Dooge (1973) ha desarrollado una ecuación de convección-difusión basada en la ecuación completa de la cantidad de movimiento. De esta manera, Dooge extendió el concepto de onda de difusión hasta comprender las ondas cinemáticas-dinámicas mixtas (Tabla 10-2). Cuando todos los términos se incluyen en la formulación, la difusividad hidráulica es esencialmente una difusividad hidráulica dinámica, expresada para canales hidráulicamente anchos como sigue:
|
qo F 2 νhF = _______ ( 1 - ______ ) 2 So 4 | (10-85) |
Ponce (1991) ha expresado la difusividad hidráulica dinámica en términos del número de Vedernikov:
|
qo νhV = _______ ( 1 - V 2 ) 2 So | (10-86) |
La Ecuación 10-86 es más completa que la Ec. 10-83. Las ecuaciones tienden a ser equivalentes sólamente para el caso V ≅ 0, es decir, para números de Froude muy pequeños. Cuando se utiliza la Ec. 10-86 con V = 1, la difusividad hidráulica se anula, lo cual no ocurre con la Ec. 10-83, para la cual la difusividad hidráulica sigue siendo finita.
10.5 MÉTODO MUSKINGUM
|
|
El método Muskingum fue desarrollado en relación con el diseño de planes de protección de avenidas en la cuenca del río Muskingum, en Ohio, Estados Unidos, de allí su nombre (Fig. 10-10) (McCarthy, 1938). Es el método más utilizado para el tránsito de avenidas, con numerosas aplicaciones a nivel mundial.
Fig. 10-10 El río Muskingum en la vecindad de Marietta, Ohio. |
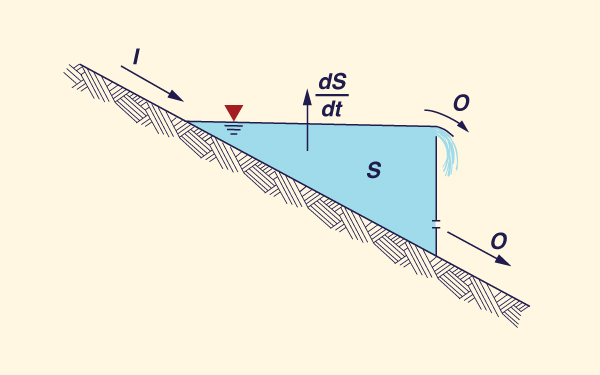
El método está basado en la ecuación diferencial de almacenamiento (Fig. 10-11):
dS | (10-87) |
en la cual I = entrada, O = salida, y S = almacenamiento (volumen).
Fig. 10-11 Definición de entrada, salida y almacenamiento en un reservorio. |
En un canal ideal, el almacenamiento es una función de los flujos de entrada y salida. En contraste, en un reservorio ideal, el almacenamiento es únicamente función del flujo de salida. En el método de Muskingum, el almacenamiento es una función linear de los flujos de entrada y salida:
| S = K [ X I + ( 1 - X ) O ] | (10-88) |
donde S = [volumen de] almacenamiento; I = flujo de entrada;
O = flujo de salida;
K = constante de tiempo, o coeficiente de almacenamiento;
y
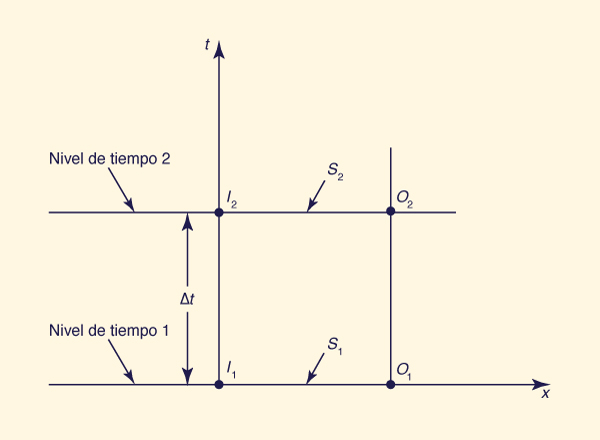
Para derivar la ecuación de tránsito Muskingum,
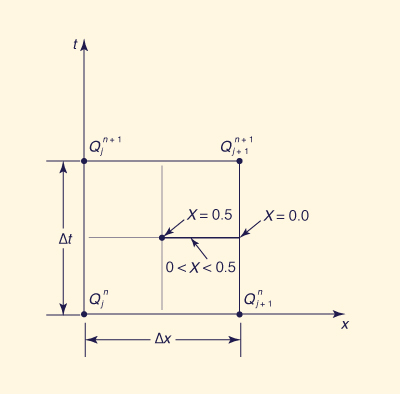
la Ec. 10-87 se discretiza en el plano x-t de la siguiente manera
I1 + I2 O1 + O2 S2 - S1 | (10-89) |
Fig. 10-12 Discretización en el plano x-t. |
La Ecuación 10-88 se expresa en los niveles de tiempo 1 y 2:
S1 = K [ X I1 + ( 1 - X ) O1 ] | (10-90) |
S2 = K [ X I2 + ( 1 - X ) O2 ] | (10-91) |
Sustituyendo las Ecs. 10-90 y 10-91 en la Ec. 10-89 y resolviendo para O2 resulta en la ecuación de tránsito:
| O2 = C0 I2 + C1 I1 + C2 O1 | (10-92) |
en la cual C0, C1 and C2 son coeficientes definidos en términos de Δt, K, y X como sigue:
( Δt / K ) - 2X | (10-93a) |
( Δt / K ) + 2X | (10-93b) |
2(1 - X) - ( Δt / K ) | (10-93c) |
Dado que C0 + C1 + C2 = 1, los coeficientes de tránsito pueden ser interpretados como coeficientes de ponderación.
Dados:
- Un hidrograma de entrada,
- Una condición inicial de flujo,
- Un intervalo de tiempo seleccionado Δt, y
- Los parámetros de tránsito X y K,
los coeficientes de tránsito se pueden calcular con la Ec. 10-93, y luego el hidrograma de salida con la Ec. 10-92.
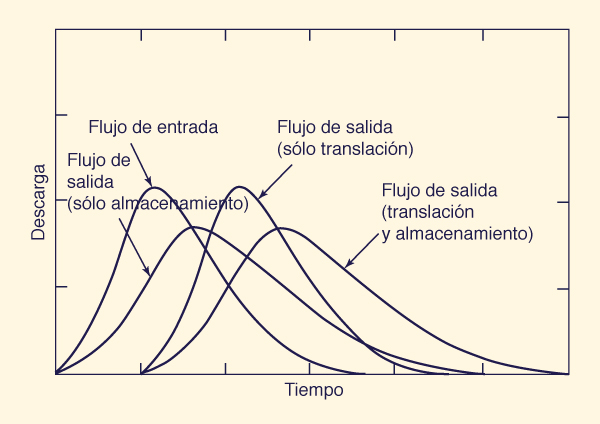
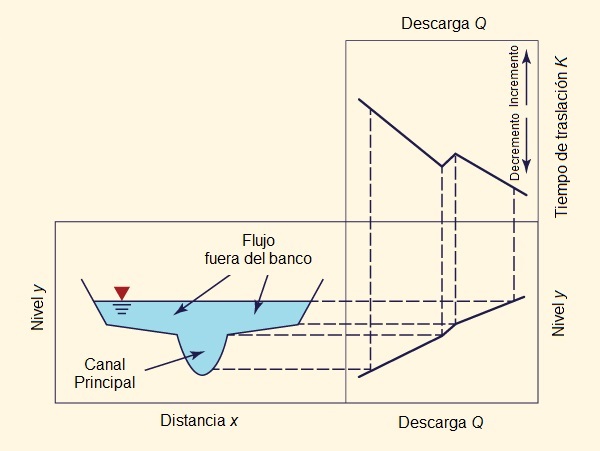
Los parámetros X y K están relacionados con las características del flujo y del canal. El parámetro K se interpreta como el tiempo de viaje de la onda de avenida, desde el extremo aguas arriba hasta el extremo aguas abajo del tramo bajo consideración. En efecto, K representa la traslación o convección de la onda de avenida (Fig. 10-13).
El parámetro X representa el almacenamiento. Para cada evento, hay un valor de X para el cual el almacenamiento en el hidrograma de salida calculado coincide con el del hidrograma de salida medido. El efecto del almacenamiento es reducir el flujo y atenuar el hidrograma (Fig. 10-13); por lo tanto, el término almacenamiento se utiliza a menudo de manera intercambiable con los términos difusión y atenuación del pico de la onda.
Fig. 10-13 Traslación y almacenamiento en el tránsito de avenidas. |
El parámetro de tránsito K es una función de la longitud del tramo del canal y la velocidad [celeridad] de la onda de avenida; por el contrario, el parámetro X es una función de las características de flujo y del canal que producen difusión del escurrimiento. En el método de Muskingum, X se interpreta como un factor de ponderación y se restringe al intervalo 0 ≤ X ≤ 0.5. Los valores de X > 0.5 producen una amplificación del hidrograma (es decir, una difusión negativa), la cual no está de acuerdo con la realidad (bajo los números de Froude F < 2, aplicables a los flujos de avenidas).
Cuando K = Δt y
En el método Muskingum, los parámetros K y X se determinan por calibración mediante el uso de registros de aforos. Las mediciones simultáneas de los caudales de entrada y salida, en un tramo del río o corriente, se utilizan junto con un procedimiento de prueba y error, llevando a la determinación de K y X (véase el Ejemplo 10-1). El procedimiento es tedioso y carece de capacidad de predicción. Los valores de K y X así determinados son válidos solamente para el tramo en estudio y para el evento utilizado en la calibración. La extrapolación a otros tramos o a otros eventos (de diferente magnitud) dentro del mismo tramo suele no ser justificada (Cunge, 1969).
Cuando se dispone de datos suficientes, la calibración se puede realizar para varios eventos, de diferente magnitud, cubriendo así un amplio rango de niveles de avenidas. De esta manera, se puede obtener la variación de K y X en función del nivel de la avenida. En la práctica, K es más sensible al nivel de avenida que X. La Figura 10-14 muestra un esquema de la variación del tiempo de translación K con la descarga y la superficie del agua.
Fig. 10-14 Variación del tiempo de traslación K en función de la descarga y la superficie del agua. |
Ejemplo 10-1.
La Columna 2 de la Tabla 10-4 contiene un hidrograma de entrada a un tramo de río. El flujo base es de
352 m3/s. Utilizando el método de Muskingum, haga el tránsito de este
hidrograma a través del tramo, utilizando
K = 2 d y X = 0.1.
En primer lugar, es necesario seleccionar un intervalo de tiempo
Δt.
En este caso, es conveniente elegir La Columna 1 muestra el tiempo, en días.
La Columna 2 muestra las ordenadas del hidrograma de entrada, en metros cúbicos
por segundo.
Las Columnas 3-5 muestran los flujos parciales.
Siguiendo la Ec. 10-91, las Cols. 3-5 se suman para obtener la Col. 6, la cual
muestra las ordenadas del hidrograma de salida, en metros cúbicos por segundo.
El flujo de salida
en el inicio (día 0) es igual al flujo de entrada en
el inicio:
352 m3/s. El flujo de entrada en el día 1 multiplicado
por C0 se coloca en la Col. 3, día 1: 76.6 m3/s.
El flujo de entrada en el día 0 multiplicado por
C1 se coloca
en la Col. 4, día 1: 107.1 m3/s.
El flujo de salida en el día 0
multiplicado por C2 se coloca en la Col. 5, día 1: 199 m3/s.
Las Columnas 3-5 del día 1 se suman para obtener la Col. 6: 76.6 + 107.1 + 199.0 = 382.7 m3/s.
Los demás cálculos se realizan de manera similar (recursiva) hasta que se hayan
obtenido todas los flujos de salida en la Col. 6.
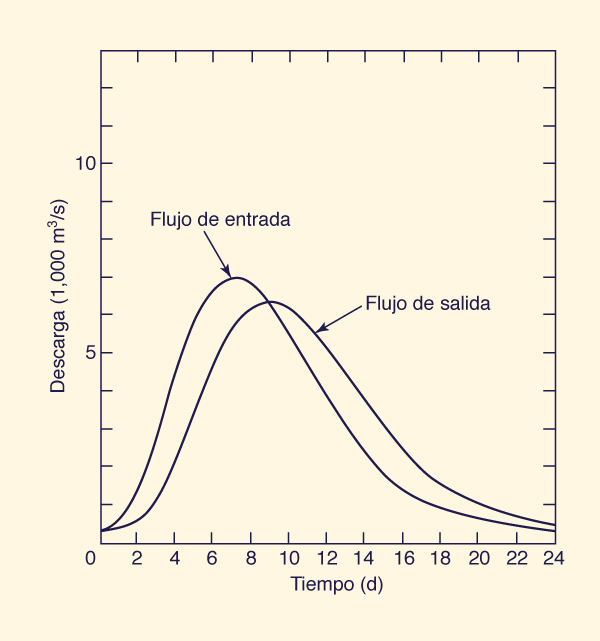
La Figura 10-5 muestra
los hidrogramas de entrada y salida.
El pico del hidrograma de salida es de
Fig. 10-15 Tránsito de avenidas utilizando el método Muskingum.
CÁLCULO EN LÍNEA.
Usando ENLINEA TRANSITO04,
la respuesta es esencialmente la misma que la de la Col. 6, Tabla 10-4.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
El Ejemplo 10-1 ha ilustrado la etapa predictiva del método Muskingum, en el cual los parámetros de tránsito se conocen de antemano. Si no se conocen los parámetros, es necesario primero realizar una calibración. El Ejemplo 10-2 ilustra el procedimiento de prueba y error para calibrar los parámetros de tránsito del método Muskingum.
Ejemplo 10-2.
Utilice el hidrograma de salida calculado en el Ejemplo 10-1,
junto con el hidrograma de entrada, para calibrar el método Muskingum, es decir,
para calcular los parámetros de tránsito
K y X.
El procedimiento se resume en la Tabla 10-5.
La columna 1 muestra el tiempo, en días.
La columna 2 muestra el flujo de entrada, en metros cúbicos por segundo.
La columna 3 muestra el flujo de salida, en metros cúbicos por segundo.
La columna 4 muestra el [volumen de] almacenamiento del canal, en (metros cúbicos por segundo)-días.
El almacenamiento del canal en el inicio se supone que es 0,
y este valor se coloca en la Col. 4,
El almacenamiento del canal se calcula mediante la solución de la Ec. 10-89 para
S2:
Se prueban varios valores de X, dentro del rango de 0.0 a 0.5; por ejemplo, en este caso, los valores 0.1, 0.2 y 0.3.
Para cada valor de X, se calculan los flujos ponderados
[ XI + ( 1 - X ) O ], los cuales se muestran en las Cols. 5-7.
Cada uno de los flujos ponderados se grafica en función
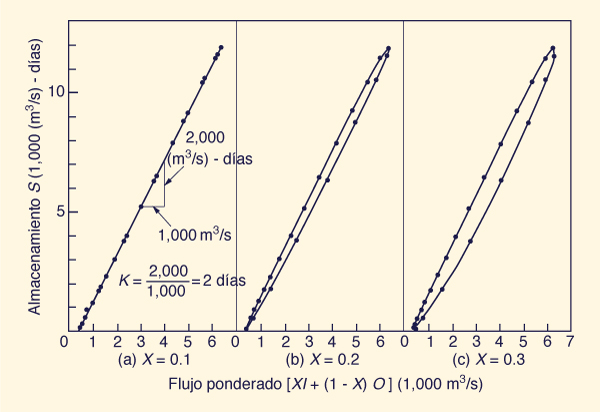
del almacenamiento (Col. 4), como se muestra en la Fig. 10-16.
El valor de X para el cual el gráfico del almacenamiento vs.
el flujo ponderado se acerca más a una línea se toma
como el valor correcto de X.
En este caso, X = 0.1, como se muestra en la
Siguiendo la Ec. 10-88, el valor de K se obtiene a partir de la Fig. 10-16 (a) mediante el
cálculo de la pendiente de la función de almacenamiento vs. el flujo ponderado.
En este caso, el valor de K es igual a: K = [2,000
Este ejemplo confirma que K = 2 días y X = 0.1 son los parámetros
de tránsito del método Muskingum para los hidrogramas de entrada y salida dados (Ejemplo 10-1).
Fig. 10-16 Calibración de los parámetros de tránsito del método Muskingum. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
La estimación de los parámetros de tránsito es absolutamente necesaria para la aplicación del método Muskingum. Los parámetros no son constantes y tienden a variar con el flujo. Si los parámetros de tránsito pudieran relacionarse con el flujo y las características del canal, no sería necesaria la calibración por prueba y error. El parámetro K podría estar relacionado con la longitud del tramo y la velocidad de la onda de avenida, mientras que X podría estar relacionado con las características de difusividad del flujo y del canal. Estas cconsideraciones constituyen la base del método Muskingum-Cunge, el cual se trata en la siguiente sección.
10.6 MÉTODO MUSKINGUM-CUNGE
|
|
El método Muskingum requiere de una calibración con el fin de identificar los parámetros de tránsito (Ejemplo 10-2). El procedimiento se basa en hidrogramas de entrada y salida medidos, tal como se muestra en Cols. 2 y 3 de la Tabla 10-5. Por lo tanto, una estación de aforo es absolutamente necesaria para que el método Muskingum sea utilizado correctamente. En otras palabras, el método puede ser utilizado únicamente en tramos del río que tengan registros de aforos.
A diferencia del método Muskingum, el método Muskingum-Cunge requiere de información hidráulica, en vez de hidrológica, para calcular los parámetros de tránsito. Los datos hidráulicos consisten de datos geomorfológicos tales como la pendiente del canal y las características de la sección transversal. El método Muskingum-Cunge no requiere explícitamente de una estación de aforo, por lo que puede ser aplicado a cualquier tramo, siempre y cuando la información hidráulica/geomorfológica esté disponible.
El método Muskingum se deriva mediante la combinación de: (1) la ecuación
diferencial de almacenamiento, es decir, la ecuación de continuidad
expresada en forma de diferencial total
Los puntos descritos anteriormente parecen ser las únicas similaridades entre los dos métodos. El método Muskingum se expresa a través de todo el tramo, basándose en el [volumen de] almacenamiento y la capacidad de describir la difusión de la onda de avenida (véase el Ejemplo 10-1). Por otro lado, el método Muskingum-Cunge se expresa, con los datos especificados, en las secciones transversales, y se basa en una discretización de la ecuación de la onda cinemática, la cual aparentemente no se difusiona. Sin embargo, los cálculos utilizando el método Muskingum-Cunge muestran que es capaz de describir la difusión de la onda de una manera similar a la del método Muskingum.
Cunge (1969) explicó la difusión de la forma discretizada de la ecuación de la onda cinemática en términos de la difusión numérica del propio esquema (véase el recuadro siguiente). De esta manera, Cunge fué capaz de explicar la aparente contradicción. Los métodos Muskingum y Muskingum-Cunge tienen la misma base teórica. Los parámetros de tránsito del método Muskingum son hidrológicos, basados en el almacenamiento, aplicables a un tramo, y determinados por calibración utilizando datos hidrológicos (aforos). En cambio, los parámetros de tránsito del método Muskingum-Cunge son hidráulicos, distribuídos (en una sección transversal), y basados exclusivamente en datos hidráulicos.
|
Breve explicación del concepto de difusión numérica 1
La existencia de difusión en un esquema numérico requiere de mayor elaboración. Hayami (1951) observó que en la Naturaleza, las irregularidades producen difusión física. El mismo proceso es extendible al mundo computacional: Las irregularidades producen difusión numérica. Las irregularidades se interpretan como los errores inherentes al cálculo numérico, entre los que destacan en forma preponderante los errores de truncación. La sustitución de una ecuación diferencial parcial, basada en ∂, con una ecuación diferencial finita, basada en Δ, produce errores, los cuales, cuando se expresan en conjunto, se manifiestan como difusión. Por lo tanto, la difusión numérica es la analogía en el mundo computacional a la difusión física en el mundo real. 1 Véase Cunge (1969) para una explicación detallada de la difusión numérica en relación con el método Muskingum. |
La ecuación de tránsito Muskingum-Cunge
Para derivar la ecuación de tránsito Muskingum-Cunge,
la ecuación de la onda cinemática
X (Q j n+1 - Q j n ) + (1 - X) (Q j+1n+1 - Q j+1 n ) |
|
(Q j+1 n - Q j n ) + (Q j+1n+1 - Q
j n+1 ) c _______________________________________ = 0 2 Δx | (10-94) |
en la cual c = βV es la celeridad de la onda cinemática.
Figure 10-17 Discretización de la ecuación
de la onda cinemática |
Resolviendo la Ec. 10-94 para la descarga desconocida conduce a la siguiente ecuación de tránsito:
| Q j+1 n+1 = C0 Q j n+1 + C1 Q j n + C2 Q j+1 n | (10-95) |
Los coeficientes son:
c ( Δt / Δx ) - 2X | (10-96a) |
c ( Δt / Δx ) + 2X | (10-96b) |
2(1 - X) - c ( Δt / Δx ) | (10-96c) |
Definiendo el tiempo de traslado o de viaje como sigue:
|
Δx K = ______ c | (10-97) |
puede observarse que los conjuntos de ecuaciones Ec. 10-93 y Ec. 10-96 son los mismos.
La Ecuación 10-97 confirma que K es efectivamente el tiempo de viaje de la onda de avenida, es decir, el tiempo que toma una descarga dada en trasladarse a través del tramo Δx con la celeridad [de la onda cinemática] c.
Propiedades numéricas
El número de Courant se define como la relación entre la celeridad física
(c) y la celeridad numérica, o celeridad de la malla,
Δt | (10-98) |
La Ecuación 10-95 es el análogo numérico de la Ec. 10-55 y, por lo tanto, está sujeta a difusión y dispersión numéricas. La difusión numérica es el error de segundo orden; la dispersión numérica es el error de tercer orden. Las siguientes condiciones se cumplen:
Para X = 0.5 y C = 1, la ecuación tiene una precisión de tercer orden, es decir, la solución numérica es igual a la solución analítica (de la ecuación de la onda cinemática).
Para X = 0.5 y C ≠ 1, la ecuación tiene una precisión de segundo orden, exhibiendo solamente dispersión numérica.
Para X < 0.5 y C ≠ 1, la ecuación tiene una precisión de primer orden, exhibiendo ambas difusión y dispersión numéricas.
Para X < 0.5 and C = 1, la ecuación tiene una precisión de primer orden, exhibiendo solamente difusión numérica.
Estas relaciones se resumen en la Tabla 10-6.
| ||||||||||||||||||||||||||||||
En la práctica, la difusión numérica puede ser utilizada para simular la difusión física de la onda de avenida. Expandiendo la función discreta Q (jΔx, n Δt) en serie de Taylor alrededor del punto de malla (jΔx, n Δt), se deriva el coeficiente de difusión numérica del esquema de Muskingum (Cunge, 1969) (Apéndice B):
1 | (10-99) |
en la cual νn es el coeficiente de difusión numérica. Esta ecuación revela lo siguiente:
Para X = 0.5 no hay difusión numérica, aunque aún existe una cierta dispersión numérica para
C ≠ 1; Para X > 0.5, el coeficiente de difusión numérica es negativo, es decir, existe amplificación numérica, lo que explica el comportamiento del método de Muskingum para este rango de valores de X;
Para Δx = 0, el coeficiente de difusión numérica es cero, lo cual es claramente el caso trivial.
Se puede obtener una ecuación predictiva para X igualando la difusividad hidráulica νh (Ec. 10-83) con el coeficiente de difusión numérica del esquema de Muskingum νn (Ec. 10-99). Esto conduce a la siguiente expresión:
1 qo | (10-100) |
Cuando X se calcula por medio de la Ec. 10-100, el método Muskingum se conoce como método Muskingum-Cunge. El parámetro X se puede calcular en función de las siguientes propiedades numéricas y físicas:
Longitud del tramo Δx,
Descarga de referencia por unidad de ancho qo,
Celeridad de la onda cinemática c, y
Pendiente de fondo So.
Cabe señalar que la Ec. 10-100 se ha derivado haciendo coincidir
la difusión física con la difusión numérica (un proceso de segundo orden),
y no toma en cuenta la dispersión (un proceso de tercer orden).
Por lo tanto, con el fin de simular correctamente la difusión de la onda
con el método Muskingum-Cunge, es necesario optimizar la
difusión numérica (con la Ec. 10-100), y a la vez, minimizar la dispersión numérica manteniendo
el valor de C ≅ 1.
|
La ventaja del método Muskingum-Cunge
Una característica única del método Muskingum-Cunge,
la cual lo diferencía de otros esquemas numéricos de ondas cinemáticas,
es la invariabilidad del hidrograma calculado en la sección aguas abajo.
Si se reduce al mínimo la dispersión numérica (C ≅ 1),
el hidrograma calculado será esencialmente el mismo, independientemente del número de
subtramos utilizados en el cálculo. Esto se debe a que
X es una función
de Δx |
Ponce y Yevjevich (1978) han ofrecido una versión mejorada del método Muskingum-Cunge. La difusividad de la malla se define como la difusividad numérica para el caso especial X = 0. A partir de la Ec. 10-99, la difusividad de la malla es:
Δx | (10-101) |
El número de Reynolds de la malla D se define como la
relación de la difusividad hidráulica
qo | (10-102) |
Por lo tanto:
1 | (10-103) |
Las Ecuaciones 10-101 y 10-102 implican que para valores muy pequeños de Δx, D puede ser mayor que 1, conduciendo a valores negativos de X. En efecto, para la longitud característica del tramo
qo | (10-104) |
el número de Reynolds de la malla es D = 1, y X = 0. Por lo tanto, en el método Muskingum-Cunge, las longitudes de tramo más cortas que la longitud característica (Ec. 10-104) resultan en valores negativos de X. Esto puede compararse con el método Muskingum clásico (Sección 10.4), en el cual X está limitado al rango 0.0 ≤ X ≤ 0.5. En el Muskingum clásico, X se interpreta como un factor de ponderación. Las Ecs. 10-101 y 10-102 muestran que los valores no negativos de X están asociados con tramos largos, típicos del cálculo manual utilizado en las primeras aplicaciones del método Muskingum.
Sin embargo, en el método Muskingum-Cunge, X se interpreta como un factor de igualación de momento o de equidad de difusión. Por lo tanto, los valores negativos de X son enteramente posibles. Esta característica permite el uso de tramos más cortos, lo cual no sería posible si X se limitara a valores no negativos.
Los coeficientes de tránsito Muskingum-CungeLa sustitución de las Ecs. 10-98 y 10-100 en la Ec. 10-96 conduce a coeficientes de tránsito expresados en términos de los números de Courant y Reynolds de la malla:
-1 + C + D | (10-105a) |
1 + C - D | (10-105b) |
1 - C + D | (10-105c) |
El cálculo de los parámetros de
tránsito C y D
se puede realizar de varias maneras.
La celeridad de la onda se puede calcular
ya sea con la Ec. 10-57 o la Ec. 10-59.
Con la
Con la ayuda de las Ecs. 10-98 y 10-102, los parámetros de tránsito pueden basarse en las características de flujo. Los cálculos pueden proceder de modo linear o no linear. En el modo linear, los parámetros de tránsito se basan en valores de referencia y se mantienen constantes durante el cálculo en el tiempo. La elección de flujo de referencia tendrá efecto en los resultados calculados, aunque es probable que el impacto global sea pequeño (Ponce y Yevjevich, 1978). Para aplicaciones prácticas, se puede utilizar como valor de referencia ya sea un valor promedio del flujo o un valor máximo. El valor máximo tiene la ventaja de que se puede determinar fácilmente; no obstante, es posible obtener una mejor aproximación mediante el uso de un valor medio.
El cálculo linear se conoce como el método Muskingum-Cunge de parámetro constante, para distinguirlo del método Muskingum-Cunge de parámetro variable, en el cual los parámetros de tránsito pueden variar con el flujo. El método del parámetro constante se asemeja al método Muskingum, con la diferencia de que los parámetros de tránsito se basan en las características hidráulicas del tramo en lugar de datos históricos del flujo.
Ejemplo 10-3.
Utilice el método Muskingum-Cunge
de parámetro constante para hacer el tránsito de la onda de avenidas
con los siguientes flujos y
características del canal:
flujo de avenida:
Qp = 1000 m3/s; flujo
de base
La velocidad media (basada en la descarga máxima) es
V = Qp /Ap = 2.5 m/s. La celeridad de la onda es
CÁLCULO EN LÍNEA.
Usando ONLINE ROUTING05, la respuesta es esencialmente
la misma que la de la Col. 6, Tabla 10-7.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Requisitos de resolución espacial y temporal
Cuando se utiliza el método Muskingum-Cunge, es necesario asegurar que los valores de Δx and Δt sean lo suficientemente pequeños para asegurar una buena aproximación a la forma real del hidrograma. Se recomienda un valor mínimo de tp /Δt = 5, para aquellos hidrogramas que crecen lentamente. Este requisito usualmente da como resultado que el tiempo del hidrograma se resuelva en por lo menos 15 a 25 puntos discretos, lo cual se considera adecuado para el tránsito de la onda.
A diferencia de la resolución temporal, no hay criterios bien definidos para la resolución espacial. Un criterio probado por la experiencia se basa en el hecho de que los números de Courant y de Reynolds de la malla están inversamente relacionados con la longitud del tramo Δx. Por lo tanto, para mantener Δx lo suficientemente pequeño, los números de Courant y de Reynolds de la malla se deben mantener suficientemente grandes. Esto conduce al criterio práctico (Ponce y Theurer, 1982):
C + D ≥ 1 | (10-106) |
la cual se puede escribir como sigue: -1 + C + D ≥ 0. Esto confirma la necesidad de evitar valores negativos de C0 en el tránsito con el método Muskingum-Cunge (ver la Ec. 10-105a). La experiencia ha demostrado que los valores negativos de C1 o C2 no afectan negativamente a la precisión del método.
No obstante la Ec. 10-106, el método Muskingum-Cunge funciona mejor cuando la dispersión numérica es minimizada, es decir, cuando C ≅ 1. Es probable que los valores de C sustancialmente menores que 1 causen las notorias caídas, o salidas negativas de flujo, en algunas porciones del hidrograma calculado. Esta anomalía computacional es atribuída a una excesiva dispersión numérica y debe ser evitada.
El método Muskingum-Cunge no linearLa ecuación de la onda cinemática, Ec. 10-55, es no linear debido a que la celeridad varía con la descarga. La no linearidad es leve, entre otras cosas porque la variación de la celeridad de onda está generalmente restringida dentro de un rango pequeño. Sin embargo, en ciertos casos puede ser necesario tomar en cuenta esta no linearidad. Esto se puede lograr de dos maneras: (1) durante la discretización, al permitir que la celeridad de la onda varíe, lo que resulta en un esquema numérico no linear, el cual puede ser resuelto por medios iterativos; o (2) después de la discretización, mediante la variación de los parámetros de tránsito, como en el método Muskingum-Cunge de parámetro variable (Ponce y Yevjevich, 1978). El segundo enfoque es particularmente útil si el efecto no linear general es pequeño, lo cual a menudo es el caso.
El método Muskingum-Cunge de parámetro variable presenta una pequeña y a veces perceptible mejora sobre el método de parámetro constante. Las diferencias son probablemente más marcadas en tramos muy largos y/o grandes variaciones en los niveles de flujo. Los hidrogramas de avenidas calculados con parámetros variables muestran una cierta cantidad de distorsión, ya sea el empinamiento de la onda, en el caso de los flujos contenidos dentro del banco, o el aplanamiento, en el caso de los flujos que se desbordan. Esta es una manifestación física del efecto no linear, es decir, diferentes niveles de flujo viajan con diferentes celeridades (Fig. 10-14). Por el contrario, los hidrogramas de avenidas calculados utilizando parámetros constantes no muestran distorsión de la onda.
Análisis comparativo de los métodos Muskingum y Muskingum-CungeEl método Muskingum-Cunge representa una alternativa con base física del método Muskingum. A diferencia del método Muskingum, en la cual los parámetros son calibrados usando datos de aforos, en el método Muskingum-Cunge los parámetros se calculan basándose en las características hidráulicas del canal. Esto hace posible el tránsito de avenidas sin necesidad de calibración de parámetros. Más importante aún, el método Muskingum-Cunge hace posible de manera extensa el tránsito de avenidas en corrientes no aforadas, con una expectativa razonable de precisión. Con el uso de parámetros variables, las propiedades no lineares de las ondas de avenida (las cuales de otro modo solamente podrían ser obtenidas por procedimientos numéricos más elaborados) pueden describirse en el contexto de la formulación tipo Muskingum.
Al igual que el método Muskingum, el método Muskingum-Cunge
está limitado a las ondas de difusión. Además, el método
Muskingum-Cunge se basa en una curva de gasto de valor único, no tomando
en cuenta flujos no permanentes de importancia ni
flujos que muestren curvas de histéresis notables en
la curva de gasto (es decir, las ondas dinámicas; véase la siguiente sección).
Por lo tanto, el método Muskingum-Cunge es adecuado para
el tránsito en arroyos naturales sin efectos
importantes de remanso y para flujos no permanentes que puedan ser clasificados
como ondas difusivas
Cabe señalar una diferencia importante entre los métodos Muskingum y Muskingum-Cunge. El método Muskingum se basa en el concepto de almacenamiento (Ec. 10-87) y, por lo tanto, los parámetros K y X son los promedios de los tramos. El método Muskingum-Cunge, sin embargo, es de naturaleza distribuída, y sus parámetros C and D están basados en valores evaluados en secciones transversales. Por lo tanto, para que el método de Muskingum-Cunge mejore el resultado del método de Muskingum, es necesario que los parámetros de tránsito evaluados en secciones transversales sean representativos del tramo subtendido (Fig. 10-18).
Históricamente, el método Muskingum se ha calibrado usando datos de aforos. Por el contrario, el método Muskingum-Cunge se basa en características físicas, tales como curvas de gasto y los datos de secciones transversales y pendiente de fondo. Los diferentes requerimientos de datos reflejan las diferentes bases teóricas de los métodos, es decir, el concepto de almacenamiento (en el tramo) para el método Muskingum, y la teoría de la onda cinemática/difusiva distribuída (con datos en secciones transversales) para el método Muskingum-Cunge.
Figura 10-18 El río Moyán, en Lambayeque, Perú. |
10.7 ONDAS DINÁMICAS
|
|
En el flujo no permanente, el término onda dinámica se utiliza para referirse a dos tipos diferentes de ondas:
Una onda que no considera la fricción ni la pendiente de fondo, es decir, la onda [3] en la
Tabla 10-2, y-
Una onda que incluye todos los términos de la ecuación de cantidad de movimiento, es decir, la onda [5] en la Tabla 10-2.
Para evitar confusión, el primer tipo de onda [3] se conoce aquí como onda dinámica pura. El segundo tipo [5] se denomina onda cinemática-dinámica mixta, y se abrevia como onda dinámica mixta.
Ondas dinámicas puras
Conceptualmente, las ondas dinámicas puras son exactamente opuestas a las ondas cinemáticas. Mientras las ondas cinemáticas yacen al lado izquierdo del espectro de número de onda adimensional, las ondas dinámicas puras yacen al lado derecho (Fig. 10-4). Por lo tanto, su número de onda es grande, es decir, la longitud de onda L es pequeña en relación con la longitud de referencia del canal Lo (Ec. 10-30).
La celeridad relativa adimensional de la onda cinemática es constante e igual a 0.5, asumiendo la fricción de Chezy. Sin embargo, la celeridad relativa adimensional de la onda dinámica pura es igual al recíproco del número de Froude (Fig 10-3.):
1 (gho)1/2 | (10-107) |
La celeridad relativa de la onda dinámica pura es:
|
crd = (gho)1/2 | (10-108) |
La celeridad de la onda dinámica pura es:
|
cd = uo ± (gho)1/2 | (10-109) |
Por lo tanto, la onda dinámica pura tiene dos componentes, y sus celeridades son:
|
cd1 = uo + (gho)1/2 | (10-110a) |
|
cd2 = uo - (gho)1/2 | (10-110b) |
Las ondas cinemáticas y dinámicas puras comparten una característica especial: Ellas no se atenúan. Esto se debe a que la celeridad relativa adimensional permanece constante a través del espectro aplicable de números de onda adimensional (véase la Fig. 10-4).
En la práctica, las ondas dinámicas puras constituyen las ondas "cortas" que se presentan en canales de laboratorio y pequeños canales en la naturaleza. No se aplican a las ondas de avenidas, las cuales yacen al lado izquierdo del espectro de números de onda adimensional.
Ondas dinámicas mixtas
Las ondas cinemáticas dinámicas mixtas yacen hacia el
centro del espectro de números de onda adimensional (Fig. 10-4).
Conceptualmente, esta ondas son el tipo más completo de onda del flujo en canales,
ya que consideran todos los términos
de la ecuación de cantidad de movimiento
Lighthill y Whitham (1955) describen la impermanencia de las ondas dinámicas [mixtas] de la siguiente manera:
|
Lighthill y Whitham (1955) continuaron con esta declaración (op. cit., página 291):
|
En general, las ondas dinámicas mixtas no se aplican a flujos de avenida. Una vez generadas, las ondas dinámicas tienden a disiparse rápidamente, y su masa se une a la de la onda cinemática o difusiva subyacente predominante.
La excepción a la regla puede ser la onda de avenida generada por una rotura de presa, la cual típicamente es tan repentina que en realidad puede tratarse de una onda dinámica mixta. Estas ondas se atenúan muy rápidamente, lo que confirma que la teoría está correcta. Por ejemplo, la falla de la Presa Teton, en Idaho, EE.UU., el 5 de Junio de 1976 (Fig. 10-19). La onda de avenida liberada en el sitio de la presa se atenuó a una pequeña fracción (menos del 3%) de su descarga inicial en una distancia relativamente corta, medida hacia aguas abajo. Varios otros ejemplos de roturas de presas han confirmado que las ondas de avenida causadas por la rotura tienden a disiparse en forma bastante rápida.
|
Modelación de ondas dinámicas mixtas
En una solución de onda dinámica mixta, las ecuaciones de continuidad y cantidad de movimiento se resuelven mediante un procedimiento numérico, ya sea (a) el método de diferencias finitas, (b) el método de las características, o (c) el método de elementos finitos. En el método de las diferencias finitas, las ecuaciones diferenciales parciales se discretizan siguiendo un esquema numérico apropiado.
El método de las características se basa en la conversión del conjunto de ecuaciones diferenciales parciales a un conjunto relacionado de ecuaciones diferenciales ordinarias, y la solución a lo largo de una malla característica, es decir, una malla que sigue direcciones características. El método de elementos finitos resuelve un sistema de ecuaciones integrales sobre una malla de elementos finitos apropiada.
En las últimas cuatro décadas, el método de diferencias finitas se ha constituido en la forma más conveniente de obtener una solución de onda dinámica [mixta] para aplicaciones prácticas. Entre los varios esquemas numéricos que se han utilizado en relación con la onda dinámica, el esquema de Preissmann es quizás el más popular (Liggett y Cunge, 1975). Este es un esquema de cuatro puntos, centrado en las derivadas temporales y ligeramente descentrado en las derivadas espaciales, mediante el uso de un factor de ponderación θ. El hecho de que las derivadas espaciales no se encuentren justamente en el centro introduce una pequeña cantidad de difusión numérica, la cual es necesaria para controlar la estabilidad numérica del esquema no linear. Esto lleva a un esquema viable, con una precisión aceptable.
Las variables independientes utilizadas en el tránsito de onda
dinámica mixta son generalmente la descarga Q y el
Figure 10-20 Subdivisión del tramo para el cálculo de la onda dinámica mixta. |
En la práctica, la solución de onda dinámica mixta representa un incremento de un orden de magnitud en la complejidad y requerimientos de datos, cuando se compara con la solución de onda cinemática o difusiva. Su uso se recomienda en situaciones donde la onda cinemática y la onda difusiva no ofrecen una representación adecuada del fenómeno. En particular, las soluciones de onda dinámica mixta son aplicables a: (a) ondas de avenida causadas por la rotura de una presa, (b) flujo sobre pendientes muy planas o leves, (c) flujo entrante a grandes reservorios, (d) remansos fuertes, y (e) cambios de dirección del flujo. En general, la onda dinámica mixta se recomienda para los casos que justifican una determinación muy precisa de la variación no permanente de la superficie del agua.
La versión actual (versión 4.1) del modelo HEC-RAS (U.S. Army Corps of Engineers, 2010) contiene un módulo de onda dinámica mixta adecuado para aplicaciones prácticas.
La curva de gasto de la onda dinámica mixtaA las soluciones de ondas dinámicas mixtas se las conoce comúnmente como el tránsito hidráulico de avenidas. Como tal, tienen la capacidad de calcular las descargas y niveles de la superficie del agua no permanentes, cuando se provée al modelo con los datos geométricos del tramo o canal, y las condiciones iniciales y de frontera apropiadas. La importancia de las ondas dinámicas mixtas en el flujo no permanente se examina aquí comparándolas con las ondas cinemáticas y difusivas.
Las ondas cinemáticas calculan descargas no permanentes; los niveles correspondientes de la superficie del agua son posteriormente obtenidas de las curvas de gasto apropiadas. Para este propósito se utilizan las curvas de gasto de equilibrio, es decir, permanente. Las ondas difusivas pueden o no utilizar las curvas de gasto de equilibrio para calcular los niveles de la superficie del agua. Algunos métodos, por ejemplo, Muskingum-Cunge, utilizan las curvas de gasto de equilibrio, pero otras soluciones de onda difusiva pueden no limitarse a la curva de gasto de equilibrio.
Las ondas dinámicas mixtas se basan en la física de los fenómenos descritos por las ecuaciones gobernantes, generando así su propia curva de gasto no permanente. En cada sección transversal se produce una curva de gasto con histéresis, como se muestra en la Fig. 10-21. Por lo tanto, dado un nivel de la superficie de agua, la descarga es mayor en la rama ascendente del hidrograma y menor en la rama descendente. Esta curva de histéresis se debe a razones hidrodinámicas y no debe confundirse con otros curvas, que pueden ser causadas por erosión, sedimentación, o cambios en la configuración del lecho del río o canal.
Figure 10-21 Curva de gasto con histéresis en las ondas dinámicas mixtas. |
El ancho o grosor de la curva de histéresis es una medida directa del nivel de impermanencia del flujo. Los anchos más grandes corresponden a flujos altamente impermanentes. Los anchos pequeños corresponden a flujos ligeramente impermanentes, tal vez una onda difusiva. Si el ancho es prácticamente inexistente, el flujo se puede considerar como un flujo cinemático. De hecho, la suposición básica del flujo de onda cinemática es que la cantidad de movimiento puede ser simulada como un flujo uniforme, es decir, que la curva de gasto es única (de un solo valor).
De las observaciones anteriores se concluye que la importancia de las ondas dinámicas mixtas está directamente relacionada con la impermanencia del flujo y la correspondiente histéresis en la curva de gasto (Fig. 10-21). La curva de gasto con histéresis considerable se presenta en el flujo altamente impermanente, como en el caso de la onda de avenida causada por una rotura de presa. Para otros flujos no permanentes de menor consideración, las ondas cinemáticas y difusivas son una alternativa viable, siempre que su aplicabilidad pueda ser claramente establecida (Ecs. 10-67 y 10-84).
La condición de frontera aguas abajoLa modelación de una onda dinámica mixta presenta una paradoja singular: Para poder resolver el problema en forma correcta, es necesario especificar una condición de frontera dinámica aguas abajo (por lo general, una curva de gasto). Sin embargo, la condición de frontera dinámica aguas abajo se desconoce a priori. Abbott (1976) colocó esta paradoja en la perspectiva correcta cuando hizo el siguiente comentario:
|
Un artificio útil para salvar esta dificultad consiste en extender artificialmente el canal, aguas abajo, a lo largo de varios subtramos, y luego especificar una curva de gasto cinemática en la nueva sección de frontera aguas abajo (Fig. 10-22). Esto permite que la curva de gasto con histéresis pueda desarrollarse en las demás secciones transversales localizadas aguas arriba. Ponce y Lugo (2001) han utilizado un análisis de sensibilidad para demostrar que la extensión artificial del canal en una cantidad igual a la longitud del canal (es decir, el doblar la longitud) es usualmente suficiente para producir una curva de gasto con histéresis precisa en las secciones transversales de interés.
Fig. 10-22 La extensión artificial del dominio, para uso en modelos de onda
dinámica mixta, |
PREGUNTAS
|
|
¿Qué leyes de conservación se utilizan en la descripción del flujo permanente gradualmente variado?
¿Qué leyes de conservación se utilizan en la descripción del flujo no permanente gradualmente variado?
-
¿Qué fuerzas actúan sobre un volumen de control en el flujo no permamente gradualmente variado?
¿Qué tipos de ondas se usan comúnmente en el flujo no permanente en canales?
-
¿A qué tipo de problemas se aplican las ondas cinemáticas?
¿A qué tipo de problemas se aplican las ondas difusivas?
¿Cómo se define Lo?
¿Qué es y cómo se define el número de onda adimensional?
¿Cuál es la celeridad relativa adimensional de las ondas cinemáticas bajo la fricción de Chezy en canales hidráulicamente anchos?
¿Cuál es la celeridad relativa adimensional de las ondas dinámicas bajo la fricción de Chezy en canales hidráulicamente anchos?
¿Cuáles son las tres formas de expresar la celeridad convectiva de las ondas cinemáticas?
¿Cuál es el número de Froude neutralmente estable aplicable a canales triangulares bajo la fricción de Chezy?
¿Cuál es el número de Froude neutralmente estable aplicable a canales hidráulicamente anchos bajo la fricción de Manning?
¿Cuál es la base teórica del método Muskingum-Cunge?
¿Cuál es la contribución de Hayami en la teoría del tránsito de avenidas?
¿Para que valor del número de Vedernikov las difusividades hidráulicas cinemáticas y dinámicas son las mismas?
¿Para qué valor del número de Vedernikov la difusividad hidráulica dinámica es nula?
¿Qué parte del tránsito de avenidas representa el parámetro de Muskingum X?
¿Qué es la difusión numérica?
¿Qué es la dispersión numérica?
¿Cuál es la ventaja del método Muskingum-Cunge?
¿En que situación no dará buenos resultados el método de Muskingum-Cunge?
¿Cómo se debe especificar la condición de frontera aguas abajo, en un modelo de onda dinámica mixta, con el fin de obtener una mayor precisión?
PROBLEMAS
|
|
Usted está observando la subida de nivel de un río durante una avenida. El ancho del río en el punto de observación, y por alguna distancia aguas arriba es 65 m, y de acuerdo a la lectura de la curva de gasto, la descarga es Q = 70 m3/s. Estimar la descarga en un punto situado a 15.875 km aguas arriba, si la superficie del agua está subiendo a una velocidad de 9 mm/hr en su ubicación, y en 12 mm/hr en la sección transversal aguas arriba.
Un canal hidráulicamente ancho opera con un número de Froude F = 0.22. La descarga por unidad de ancho es q = 2.8 m2/s. ¿Cuáles son las dos celeridades absolutas de Lagrange?
Una onda de avenida se desplaza dentro de los bancos (sin desbordarse) a través de un tramo de río recto, de ancho de superficie T = 320 m y longitud L = 5,625 m. Por cada 1 cm de aumento de nivel de la avenida, la descarga sube 10 m3/s. ¿Cuánto tiempo se necesita para que una descarga dada viaje la longitud del tramo?
Calcular el exponente β de la curva de gasto descarga-área aplicable a un canal triangular con fricción de Chezy.
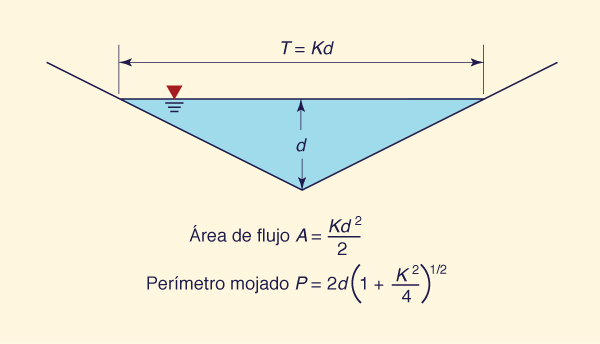
Fig. 10-23 Definición de una sección triangular transversal.
Calcular el exponente β de la curva de gasto descarga-área aplicable a un canal triangular con fricción de Manning.
Una onda de avenida tiene los siguientes datos: tiempo de subida tr = 2 hr, velocidad de referencia Vo = 2 pies/s, profundidad del flujo de referencia do = 6 pies,
pendiente de fondo So = 0.004. Determinar si ésta es una onda cinemática.Una onda de avenida tiene los siguientes datos: tiempo de subida tr = 2 hr, velocidad de referencia Vo = 2 pies/s, profundidad de flujo de referencia do = 6 pies, pendiente de fondo
So = 0.004. Determinar si ésta es una onda difusiva.Una onda de avenida tiene los siguientes datos: tiempo de subida tr = 1 hr, velocidad de referencia Vo = 2 m/s, profundidad de flujo de referencia do = 2 m, pendiente de fondo
So = 0.0004. Determinar si ésta es una onda difusiva.Usando ONLINE ROUTING 04, transitar una onda de avenida utilizando el método Muskingum. Las ordenadas del hidrograma de entrada son [25 ordenadas, comenzando en el tiempo = 0, hasta el tiempo = 24 hr]:
100, 130, 150, 180, 220, 250, 300, 360, 450, 550, 700, 550, 490, 370, 330, 310, 280, 230, 170, 150, 130, 120, 110, 105, 100.
Asumir Δt = 1 hr, K = 1 hr, X = 0.3. Reportar la descarga pico de salida y el tiempo de ocurrencia.
Usando ONLINE ROUTING 05, transitar la misma onda de avenida especificada en el problema anterior, utilizando el método Muskingum-Cunge, con los siguientes datos de entrada:
Qp = 700 m3/s, Ap = 400 m2,Tp = 88 m, Δt = 1 hr, Δx = 9.6 km, β = 1.65, So = 0.0007. Reportar la descarga pico de salida y el tiempo de ocurrencia.
BIBLIOGRAFÍA
|
|
Abbott, M. A. 1976. Computational hydraulics: A short pathology. Journal of Hydraulic Research, Vol. 14, No. 4, p. 276.
Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, Nueva York.
Craya, A. 1952. The criterion for the possibility of roll-wave formation. Gravity Waves, Circular No. 521, National Bureau of Standards, Washington, D.C. 141-151.
Cunge, J. A. (1969). On the Subject of a Flood Propagation Computation Method (Muskingum Method), Journal of Hydraulic Research, Vol. 7, No. 2, 205-230.
Dooge, J . C. I. 1973. Linear theory of hydrologic systems. Technical Bulletin No. 1468, U.S. Department of Agriculture, Washington, D.C.
Hayami, I. 1951. On the propagation of flood waves. Bulletin, Disaster Prevention Research Institute, No. 1, Diciembre.
Kibler, D. F., y D. A. Woolhiser. 1970. The kinematic cascade as a hydrologic model. Hydrology Paper No. 39, Colorado State University, Ft. Collins, Colorado.
Kleitz, M. 1877. Note sur la théorie du mouvement non permanent des liquides et sur application à la propagation des crues des rivières, (Note on the theory of unsteady flow of liquids and on application to flood propagation in rivers), Annals des Ponts et Chaussées, ser. 5, Vol. 16, 2e semestre, 133-196.
Liggett, J. A. 1975. Basic equations of unsteady flow. Chapter 2 in Unsteady flow in open channels, K. Mahmood and V. Yevjevich, eds., Water Resources Publications, Ft. Collins, Colorado.
Liggett, J. A., y J. A. Cunge. 1975. Numerical methods of solution of the unsteady flow equations. Chapter 4 In Unsteady flow in open channels, K. Mahmood and V. Yevjevich, eds., Water Resources Publications, Ft. Collins, Colorado.
Lighthill, M. J., y G. B. Whitham. 1955. On kinematic waves: I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.
McCarthy, G. T. (1938). "The Unit Hydrograph and Flood Routing," unpublished manuscript, presented at a Conference of the North Atlantic Division, U.S. Army Corps of Engineers, 24 de Junio.
Ponce, V, M., y D. B. Simons. 1977. Shallow wave propagation in open-channel flow. Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12, Diciembre, 1461-1476.
Ponce, V. M., y V. Yevjevich. 1978. Muskingum-Cunge method with variable parameters. Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY12, Diciembre, 1663-1667.
Ponce, V. M., y F. D. Theurer. 1982. Accuracy criteria in diffusion routing. Journal of the Hydraulics Division, ASCE, Vol. 108, No. HY6, Junio, 747-757.
Ponce, V, M., y D. Windingland. 1985. Kinematic shock: Sensitivity analysis. Journal of Hydraulic Engineering, ASCE, Vol. 111, No. 4, Abril, 600-611.
Ponce, V. M. 1989. Engineering hydrology: Principles and practices. Prentice Hall, Englewood Cliffs, Nueva Jersey.
Ponce, V. M. 2014. Engineering hydrology: Principles and practices. Online textbook.
Ponce, V. M. 1990. Generalized diffusion wave equation with inertial effects. Water Resources Research, Vol. 26, No. 5, Mayo, 1099-1101.
Ponce, V. M. 1991. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, Julio.
Ponce, V, M., y P. J. Porras. 1995. Effect of cross-sectional shape of free-surface instability. Journal of Hydraulic Engineering, ASCE, Vol. 121, No. 4, Abril, 376-380.
Ponce, V, M., y A. Lugo. 2001. Modeling looped ratings in Muskingum-Cunge routing. Journal of Hydrologic Engineering, ASCE, Vol. 6, No. 2, Marzo-Abril, 119-124.
Saint-Venant, B. de. 1871. Theorie du mouvement non-permanent des eaux avec application aux crues des rivieres et l' introduction des varees dans leur lit, Competes Rendus Hebdomadaires des Seances de l'Academie des Science, París, Francia, Vol. 73, 1871, 148-154.
Seddon, J. A. 1900. River hydraulics. Transactions, ASCE, Vol. XLIII, 179-243, Junio.
U.S. Army Corps of Engineers. 2010. River Analysis System: HEC-RAS, Version 4.1, Hydrologic Engineering Center, Davis, California.
| http://hidraulicadecanales.sdsu.edu |
|
170826 17:30 |