[Precipitación]   [Abstracciones Hidrológicas]   [Características de la Cuenca]   [Escurrimiento]   [Preguntas]   [Problemas]   [Bibliografía]   •   CAPÍTULO 2:  PRINCIPIOS HIDROLÓGICOS  "La descarga de un pozo de agua subterránea puede provenir de las siguientes fuentes: (1) un aumento en la recarga del acuífero al sitio de bombeo, (2) una disminución en la descarga natural del sitio, (3) una pérdida del volumen almacenado; o (4) una combinación apropiada de estos tres componentes." Charles V. Theis (1940) Este capítulo se divide en cuatro secciones. La Sección 2.1 trata sobre la precipitación, aspectos metereológicos, descripción cuantitativa, variaciones espaciales y temporales, y fuentes de información. La Sección 2.2 trata sobre las abstracciones hidrológicas de importancia en la ingenieria hidrológica, como son la intercepción, infiltración, almacenamiento superficial, y evaporación y evapotranspiración. La Sección 2 define la cuenca, su geometría y otras propiedades importantes para el análisis hidrológico. Por último, la Sección 2.4 trata sobre el análisis cualitativo y cuantitativo del escurrimiento. Los conceptos presentados en este capítulo son de caracter introductorio, en forma de información básica necesaria para un estudio posterior más detallado. 2.1  PRECIPITACIÓN [Abstracciones Hidrológicas]   [Características de la Cuenca]   [Escurrimiento]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   Introducción La ingeniería hidrológica considera al ciclo hidrológico de manera cuantitativa. La interacción entre las diferentes fases del ciclo se describen por medio de ecuaciones. Reiterando lo mencionado en el capítulo anterior, las siguiente ecuación básica relaciona el escurrimiento superficial con la precipitación: Q = P - L (2-1) en la cual Q = escurrimiento superficial, P = precipitación; y L = pérdidas, o abstracciones hidrológicas. Este último término constituye la suma de las varias abstracciones de precipitación que operan en el ciclo hidrológico. 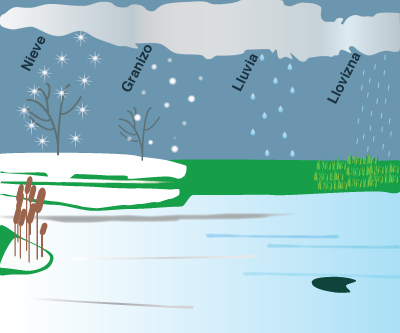La lluvia es la forma líquida de precipitación; las nevadas y el granizo son las formas sólidas. En el uso común, la palabra "lluvia" se utiliza en referencia a la precipitación. Las excepciones son los casos en que se justifica una distinción precisa entre precipitación líquida y sólida. En general, la cuenca tiene una capacidad abstractiva que actúa para reducir la precipitación total y convertirla en precipitación efectiva. La diferencia entre la precipitación total y la efectiva constituye la suma de las pérdidas. La capacidad de abstracción es una característica de la cuenca que varía con el nivel de humedad almacenada. Las abstracciones hidrológicas incluyen intercepción, infiltración, almacenamiento en superficie, evaporación y evapotranspiración. El escurrimiento es la diferencia entre la precipitación total y las abstracciones hidrológicas. Por lo tanto, los conceptos de escurrimiento y precipitación efectiva son equivalentes. Los términos de la Ecuación 2-1 se pueden expresar como velocidades (milímetros por hora, centímetros por hora, o pulgadas por hora) o, integrados en el tiempo, expresados en términos de profundidad (milímetros, centímetros o pulgadas). Visto de esta manera, una profundidad de lluvia o escorrentía es un volumen de agua distribuído uniformemente sobre toda el área de la cuenca. Aspectos meteorológicos La atmósfera de la Tierra contiene vapor de agua. La cantidad de vapor contenido en la atmósfera puede expresarse convenientemente en términos de una profundidad de agua precipitable. Ésta es la profundidad de agua que se realizaría si todo el vapor de agua en la columna de aire por encima de un área dada se condensara y cayera como precipitación sobre dicha área. Existe un límite superior en la cantidad de vapor de agua que puede existir en una columna de aire; este límite es función de la temperatura. Se considera que la columna de aire se encuentra saturada cuando contiene la cantidad máxima de vapor de agua para la temperatura dada. Al reducirse la temperatura, se produce una reducción en la capacidad de la columna de aire para contener vapor de agua. Consecuentemente, una columna de aire no saturada, es decir, aquélla que tiene menos de la cantidad máxima de vapor de agua para su temperatura, puede llegar al punto de saturación, sin añadir humedad, si la temperatura se reduce a un nivel en el cual la cantidad de vapor es suficiente para producir saturación. La temperatura a la cual el aire debe enfriarse, a presión y contenido de vapor constantes, para alcanzar la saturación se llama el punto de rocío. La condensación generalmente ocurre cerca del punto de saturación. Enfriamiento de las masas de aire. El aire puede ser enfriado de varias maneras; sin embargo, el enfriamiento adiabático por reducción de presión a través de un aumento en la elevación es el único proceso natural por medio del cual grandes masas de aire pueden ser enfriadas con la rapidez suficiente para producir una precipitación apreciable. La intensidad y profundidad de precipitación son función de la cantidad de enfriamiento y de la velocidad de ingreso de humedad. Esta última reemplaza el vapor de agua que ya ha sido convertido en precipitación. 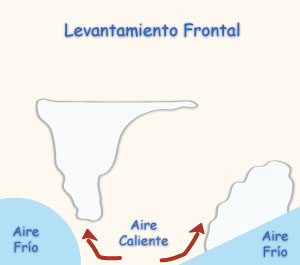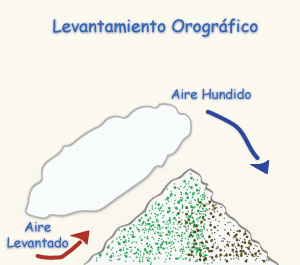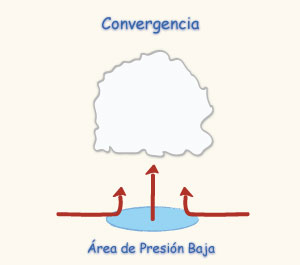El levantamiento requerido para el enfriamiento rápido de grandes masas de aire puede ser de los siguientes tipos [72]: Levantamiento frontal, Levantamiento orográfico, Levantamiento por convergencia horizontal, y Levantamiento térmico. Por lo general, más de uno de estos procesos actúa en el levantamiento asociado con las mayores intensidades y profundidades de precipitación. 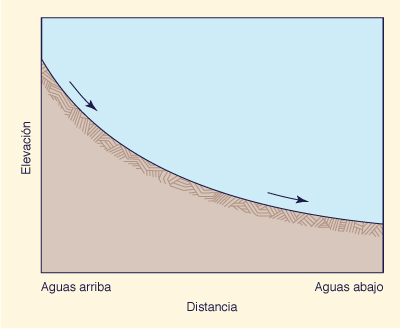El levantamiento frontal ocurre cuando una masa de aire relativamente tibia fluye hacia una más fría (y, por lo tanto, más densa); esta última es forzada hacia arriba, el aire frío actuando como una cuña. De igual manera, cuando un aire frío fluye hacia uno más caliente se produce el mismo resultado: el desplazamiento del aire caliente hacia arriba. La superficie de separación entre las dos masas diferentes de aire se denomina superficie frontal, la cual siempre se inclina hacia arriba, por encima de la masa de aire frío [Fig. 2-1 (a)]. La intersección de la superficie frontal con el terreno se denomina un frente. El levantamiento orográfico se produce cuando el aire que fluye hacia una barrera orográfica (por ejemplo, una montaña) se ve obligado a subir con el fin de pasar por encima de ésta. Las laderas de las barreras orográficas son generalmente más pronunciadas que las pendientes más pronunciadas de las superficies frontales [Fig. 2.1 (b)]. En consecuencia, el aire se enfría mucho más rápido con un levantamiento orográfico que con un levantamiento frontal. Fig. 2-1 (a)  Levantamiento frontal.    Fig. 2-1 (b)  Levantamiento orográfico. El levantamiento por convergencia horizontal también es importante en la producción de nubes y de precipitación. La convergencia se produce cuando los campos de presión y de velocidad de viento actúan para concentrar el aire en un área específica; por ejemplo, un área de presión baja. Si esta convergencia se lleva a cabo en las capas inferiores de la atmósfera, aquélla fuerza al aire hacia arriba, resultando en su enfriamiento [Fig. 2-1 (c)]. Aun cuando la precipitación no sea el resultado de la convergencia solamente, esta última usualmente contribuye a una precipitación más intensa. El levantamiento térmico es causado por un calentamiento local; a medida que el aire se calienta, se ve obligado a elevarse, lo que produce su enfriamiento. Si el aire local que ha sido calentado contiene la humedad suficiente y se eleva lo necesario, se alcanza la saturación, con la formación de nubes cúmulos. El levantamiento térmico es más pronunciado en la(s) estación(es) caliente(s) [Fig. 2-1 (d)]. Es probable que las precipitaciones asociadas con el levantamiento térmico se dispersen geográficamente, cubriendo un área grande. En regiones relativamente planas, la mayor actividad convectiva se produce sobre las superficies más calientes; contrariamente, en zonas montañosas, aquélla se produce en los picos y crestas más altas. Fig. 2-1 (c)  Levantamiento por convergencia horizontal.    Fig. 2-1 (d)  Levantamiento térmico. Condensación del vapor de agua a estado líquido o sólido. La condensación es el proceso por el cual el vapor de agua en la atmósfera se convierte en gotitas de líquido o, a bajas temperaturas, en cristales de hielo. Los resultados del proceso son a menudo, pero no siempre, visibles en forma de nubes, las cuales son gotitas líquidas de agua o cristales de hielo, o una mezcla de los dos. La saturación no necesariamente resulta en la condensación; se requieren núcleos de condensación para la conversión de vapor de agua a gotas. Entre los núcleos de condensación más eficaces se encuentran algunos productos de combustión y las partículas de sal del mar. Por lo general hay suficientes núcleos de condensación en el aire para producir la condensación cuando el vapor de agua alcanza el punto de saturación. Crecimiento de las gotas y cristales de hielo a tamaño de precipitación. Cuando se enfría el aire por debajo de su saturación inicial, y la disminución de temperatura y condensación continúan, las gotitas líquidas o cristales de hielo tienden a acumularse en la nube resultante. La velocidad a la que este exceso de humedad líquida y sólida se precipita de la nube depende de: (1) la velocidad de la corriente ascendente que produce el enfriamiento, (2) la tasa de crecimiento a gotas de agua lo suficientemente pesadas para precipitarse a través de la corriente ascendente, y (3) la entrada de vapor de agua en cantidad suficiente para reemplazar a la humedad precipitada. Generalmente, las gotas de agua en una nube típica tienen un radio promedio de cerca de 0.01 mm y pesan tan poco que una corriente ascendente de solamente 0.0025 m/s es suficiente para evitar que se precipiten. No se ha definido ningún tamaño de gota que marque el límite entre aquéllas que se quedan en la nube y aquéllas que se precipitan; generalmente se estima un radio de 0.1 mm. El radio de la mayoría de las gotas de agua que precipitan es generalmente mucho mayor que 0.1 mm, y puede llegar a 3 mm. Las gotas mayores tienden a romperse en gotas más pequeñas debido a que la tensión superficial es insuficiente para soportar las distorsiones que sufre la gota en su caída a través del aire. Las gotas de 3 mm de radio tienen una velocidad máxima de aproximadamente 10 m/s; por lo tanto, sería necesaria una corriente ascendente inusualmente fuerte para evitar que una gota de este tamaño se precipite. Se han propuesto varias teorías para explicar el crecimiento de un elemento de nube hasta un tamaño en el cual se puede precipitar. Los dos procesos principales en la formación de precipitación son: (1) el proceso de cristales de hielo, y (2) el proceso de coalescencia [29]. Estos procesos pueden funcionar juntos o por separado. El proceso de cristales de hielo consiste en la presencia de cristales de hielo en una nube de agua sobreenfriada (enfriada por debajo del punto de congelación). Debido al hecho de que la presión de vapor de saturación sobre agua es mayor que sobre hielo, existe un gradiente de presión de vapor entre las gotas de agua y los cristales de hielo. Esto hace que los cristales de hielo crezcan a expensas de las gotas de agua y, en condiciones favorables, puedan alcanzar el tamaño de precipitación. El proceso de cristales de hielo es operativo sólo en las nubes de agua superenfriadas, y es más eficaz en aproximadamente -15°C. 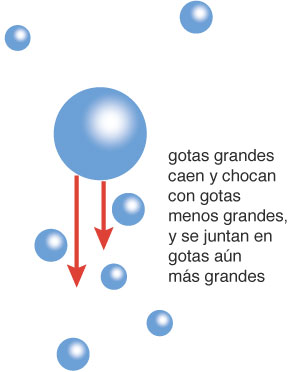El proceso de coalescencia se basa en la diferencia de velocidades de caída, lo que lleva a colisiones entre los elementos de diferentes tamaños (Fig. 2.2). La tasa de crecimiento por coalescencia depende de la gama inicial de tamaños de partículas, el tamaño de las gotas más grandes, la concentración de gotas, y los tamaños de las gotas agregadas. El campo eléctrico y la caída de carga eléctrica pueden afectar la eficiencia de colisión y, por lo tanto, pueden ser factores importantes en la producción de precipitación [71]. A diferencia del proceso de cristales de hielo, el proceso de coalescencia se produce a cualquier temperatura, y su efectividad varía entre las partículas sólidas y líquidas. Fig. 2-2  El proceso de coalescencia (cmmap.org). Formas de precipitación. La precipitación ocurre principalmente en forma de llovizna, lluvia, granizo o nieve (Fig. 2-3). La llovizna consiste de pequeñas gotas de agua líquida, por lo general entre 0.1 y 0.5 mm de diámetro, cayendo a intensidades que raramente exceden 1 mm/h. La lluvia consiste en gotas de agua líquida, en su mayoría mayores de 0.5 mm de diámetro. Las precipitaciones se refieren a cantidades de precipitación líquida. La intensidad de lluvia se puede clasificar como: ligera, hasta 3 mm/h; moderada, de 3 a 10 mm/h; e intensa, de más de 10 mm/h. Una tormenta es un evento de lluvia o precipitación que tiene una duración claramente definida. Fig. 2-3  Formas de precipitación. El granizo está compuesto de piedras de hielo sólido. Las piezas de granizo pueden ser esferoidales, cónicas, o de forma irregular, y pueden variar entre 5 y 125 mm de diámetro. Una tormenta de granizo es un evento de precipitación en forma de granizo. La nieve está compuesta de cristales de hielo, principalmente en forma hexagonal compleja, los cuales se unen para formar copos de nieve, pudiendo estos alcanzar varios milímetros de diámetro. Las nevadas son las precipitaciones en forma de nieve. Una tormenta de nieve es un evento de precipitación de nieve con una duración claramente definida. Una capa de nieve es un volumen de nieve acumulado en el suelo después de una o varias tormentas de nieve. El deshielo es el volumen de nieve que ha cambiado de estado sólido a estado líquido, el cual eventualmente puede llegar a formar parte de la escorrentía. Factores que afectan a la precipitación. La Tabla 2-1 muestra los diversos factores que afectan a la precipitación y su efecto en: (a) la disponibilidad de humedad, (b) la condensación, y (c) la coalescencia. Los factores 1 a 7 son completamente de origen natural y, por lo tanto, no están sujetos a control antropogénico. Por otro lado, el factor número 8 puede estar sujeto a controles tanto naturales como antropogénicos. El factor número 9 es el único factor que se somete sólo a controles antropogénicos. Tabla 2-1  Factores que afectan a la precipitación. No. Factor Efecto en la Descripción /Ejemplo Disponibilidad de humedad Condensación Coalescencia 1 Latitud ✓ - - El clima es tropical, templado, o polar, en función de las celdas de Hadley y Ferrell. 2 Corrientes oceánicas globales y de mesoescala ✓ ✓ - Por ejemplo, el ENSO (El Niño Oscilación del Sur). 3 Corrientes atmosféricas ✓ ✓ - Por ejemplo, la precipitación debida a un viento monzón, como en la Bahía de Bengala, India. 4 Proximidad a una fuente de humedad ✓ - ✓ Océano o gran lago interior; presencia de partículas de sal (aerosoles) provenientes del océano. 5 Posición continental relativa ✓ ✓ - Ubicación continental con respecto a una o más fuentes de humedad; levantamiento por convergencia horizontal; levantamiento frontal. 6 Estación - ✓ - El balance de radiación solar depende de la estación, ya sea primavera, verano, otoño, o invierno. 7 Presencia de barreras orográficas - ✓ - Sierras, que actúan como barreras a los movimientos de las masas de aire continentales; levantamiento orográfico. 8 Partículas atmosféricas naturales y/o antropogénicas - - ✓ A través de erupciones volcánicas o incendios, que aumentan las partículas atmosféricas, las cuales favorecen la formación de precipitación en dirección del viento. 9 Condición de la superficie del terreno (textura, color, contenido de humedad) ✓ ✓ - Determinado por el albedo de la superficie, el cual afecta el balance de radiación cerca de la superficie y hace posible el levantamiento térmico. Descripción cuantitativa de la precipitación Un evento de lluvia o tormenta describe un período de tiempo que tiene una lluvia medible y significativa, precedida y seguida por períodos sin precipitación apreciable. El tiempo transcurrido desde el principio hasta el final del evento de lluvia es la duración de la precipitación. Por lo general, la duración de la precipitación se mide en horas; sin embargo, para muy pequeñas zonas de captación puede ser medido en minutos, mientras que para las cuencas muy grandes puede ser medido en días. Las duraciones de lluvia de 1, 2, 3, 6, 12, y 24 horas son comunes en el análisis y diseño hidrológico. Para las pequeñas cuencas, las duraciones pueden ser tan cortas como 5 min; por el contrario, para las grandes cuencas fluviales, las duraciones de 2 d y mayores pueden ser apropiadas [78]. 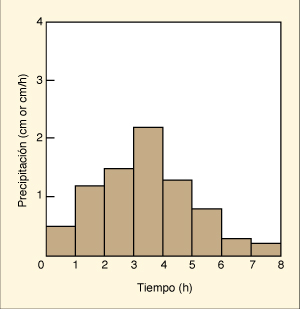La altura de lluvia se mide en mm, cm, o pulgadas, consideradas uniformemente distribuídas sobre el área de influencia. Por ejemplo, un evento de lluvia de 60 mm y 6 h produce 60 mm de profundidad en un período de 6 h. La profundidad y duración de las precipitación tiende a variar ampliamente, dependiendo de la ubicación geográfica, clima, microclima y época del año. En general, para un sitio dado, las mayores profundidades de precipitación tienden a ocurrir con menos frecuencia que las menores profundidades. Para propósitos de diseño, la profundidad de precipitación está relacionada con la frecuencia de su ocurrencia. Por ejemplo, para un sitio dado, 60 mm de lluvia con una duración de 6 horas se pueden producir en promedio una vez cada 10 años; sin embargo, 80 mm de lluvia duración de 6 h se pueden producir en promedio una vez cada 25 años. La intensidad media de precipitación es la relación de altura a duración. Por ejemplo, un evento de 60 mm en 6 h representa una intensidad media de 10 mm/h. La intensidad de lluvia, sin embargo, varía en el espacio y el tiempo, y es probable que los valores locales o instantáneos sean muy diferentes de la media espacial y temporal. Las intensidades tipicas de lluvia están en el rango de 0.1 a 30 mm/h, pero puede llegar a ser de 150 a 350 mm/h en casos extremos. La frecuencia de precipitación se refiere al tiempo medio transcurrido entre la ocurrencia de dos eventos de aproximadamente la misma profundidad y duración. El tiempo transcurrido real varía ampliamente y por lo tanto sólo puede ser interpretado en un sentido estadístico. Por ejemplo, si en una cierta ubicación se produce un evento de lluvia de 100 mm de profundidad y 6 h de duración una vez cada 50 años, la frecuencia de precipitaciones de 100 mm y de 6 h para esta ubicación sería 1 en 50 años, es decir, 1/50, o 0.02. El período de retorno, o intervalo de recurrencia, es el recíproco de la frecuencia de precipitación. En el caso del ejemplo anterior, el período de retorno correspondiente a una frecuencia de 0.02 es 50 años. En general, las más grandes profundidades de precipitación tienden a estar asociadas con períodos de retorno más largos. Cuanto más largo es el período de retorno, mayor es el registro histórico necesario para determinar las propiedades estadísticas de la distribución de precipitación máxima anual. Debido a la escasez de registros, suelen ser necesarias extrapolaciones para estimar profundidades de precipitaciones asociadas con períodos de retorno largos. Estas extrapolaciones implican un cierto grado de riesgo. Cuando este riesgo pone en peligro la vida humana, los conceptos de frecuencia de precipitación y período de retorno no se consideran adecuados para propósitos de diseño. Alternativamente, se utiliza una maximización razonable de los factores meteorológicos asociados con la precipitación extrema, lo que lleva al concepto de Precipitación Máxima Probable (PMP). Para un determinado lugar geográfico, área de influencia, duración del evento, y época del año, el valor de PMP es la mayor profundidad de precipitación justificada por la teoría. En los estudios de hidrología de inundaciones, el PMP se utiliza como base para el cálculo de la crecida máxima probable (CMF). Para ciertos proyectos, puede ser justificable una profundidad de precipitación menor que la PMP por razones económicas. Esto lleva al concepto de Tormenta Estándar de Proyecto (TEP). Usualmente, la TEP es un porcentaje adecuado del PMP aplicable, y es utilizada para calcular la Crecida Éstandar de Proyecto (CEP) (Capítulo 14). Variación temporal y espacial de la precipitación Distribución temporal de la precipitación. Por lo general, para eventos de corta duración (1 hora o menor), la intensidad de lluvia se puede expresar como un valor promedio, obtenido dividiendo la altura o profundidad de lluvia entre la duración. Para eventos más largos, los valores instantáneos de la intensidad de precipitación pueden llegar a ser más importantes, particularmente para el cálculo de los picos de avenidas. La distribución temporal de la precipitación representa la variación de la altura de lluvia dentro de una tormenta de duración dada. Esta distribución puede ser expresada en forma discreta o contínua. La forma discreta se conoce como hietograma, un histograma de altura (o intensidad) de lluvia, con incrementos de tiempo en las abscisas y la profundidad (o intensidad) de precipitación en las ordenadas, como se muestra en la Fig. 2-4 (a). 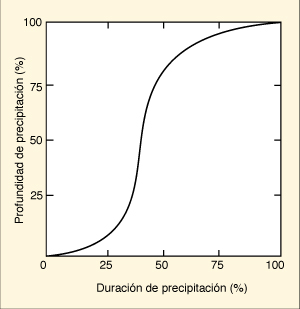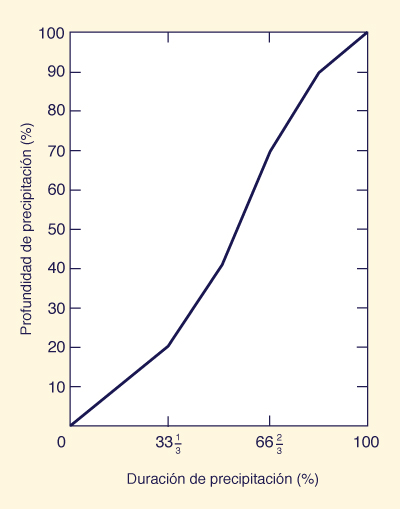La forma continua es la distribución temporal de precipitación, la cual describe la velocidad de acumulación de precipitación en el tiempo. La duración de lluvia (abscisas) y la altura de lluvia (ordenadas) pueden ser expresadas en porcentaje del valor total, como se muestra en la Fig. 2-4 (b). La distribución temporal adimensional de la precipitación se utiliza para convertir una profundidad de tormenta en un hietograma, como se muestra en el siguiente ejemplo. Fig. 2-4 (a)  Un hietograma. Fig. 2-4 (b)  Distribución temporal adimensional. Ejemplo 2-1 Usando la distribución temporal adimensional de precipitación mostrada en la Fig. 2-5, calcule el hietograma correspondiente a una tormenta de 15 cm en 6 horas. Por conveniencia, se elige un incremento de tiempo de 1 h, o 1/6 de la duración de la tormenta. Los porcentajes de precipitación acumulados (en incrementos de 1/6 de la duración de la tormenta) obtenidos a partir de la Fig. 2-3 son los siguientes: 10, 20, 40, 70, 90, y 100%. Por lo tanto, los incrementos, por hora, son los siguientes: 10, 10, 20, 30, 20, y 10%. Dada la profundidad total de tormenta de 15 cm, los incrementos (por hora) de profundidad de lluvia son los siguientes: 1.5, 1.5, 3.0, 4.5, 3.0 y 1.5 cm. Fig. 2-5  Distribución temporal adimensional de precipitaciones aplicable al Ejemplo 2-1. Distribución espacial de la lluvia. La precipitación varía no sólo temporalmente, sino también espacialmente; es decir, usualmente la misma cantidad de lluvia no cae en forma uniforme sobre toda la superficie de la cuenca. Las isoyetas se utilizan para describir la variación espacial de la precipitación. 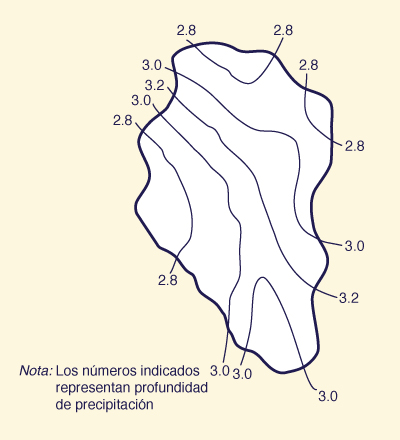La isoyeta es una línea de contorno que muestra el lugar geométrico de una cantidad dada de precipitación [Fig. 2-6 (a)]. Fig. 2-6 (a)   Isoyetas, o curvas isoyetas.    Fig. 2-6 (b)  Un ojo de tormenta. 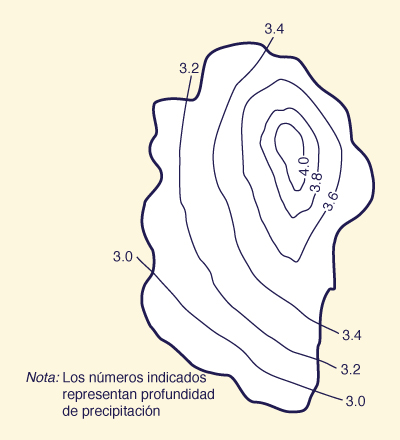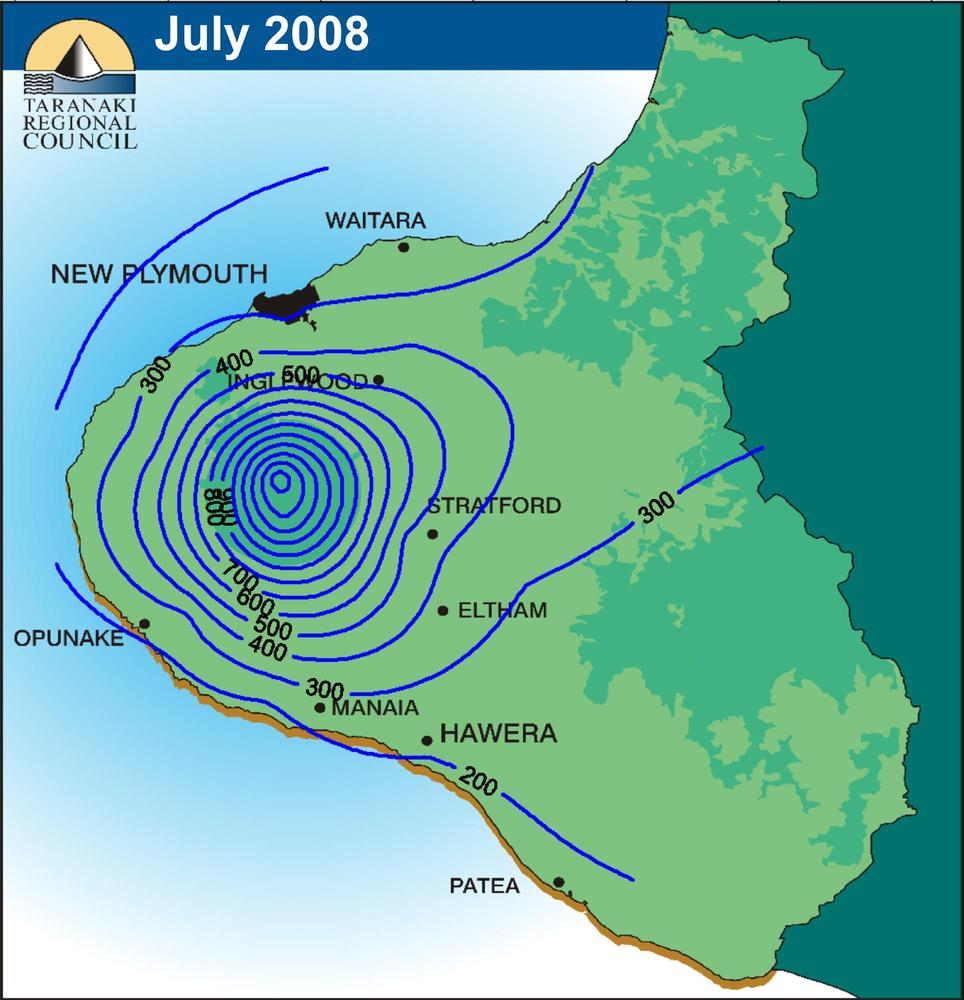Las tormentas pueden tener una distribución espacial de isoyetas concéntricas, de forma aproximadamente elíptica. Esto da lugar al término "ojo de tormenta" para referirse al centro de la tormenta [Fig. 2-6 (b)]. En general, las tormentas no son estáticas, moviéndose gradualmente en dirección aproximadamente paralela a la de los vientos predominantes. Las isoyetas también se utilizan para mostrar los patrones espaciales de lluvia correspondientes a un período de tiempo dado. Por ejemplo, la Fig. 2-7 muestra la distribución de la precipitación espacial en el mes de julio de 2008 en Taranaki, Nueva Zelanda. Fig. 2-7  Ejemplo de distribución espacial de precipitación mensual (mm). 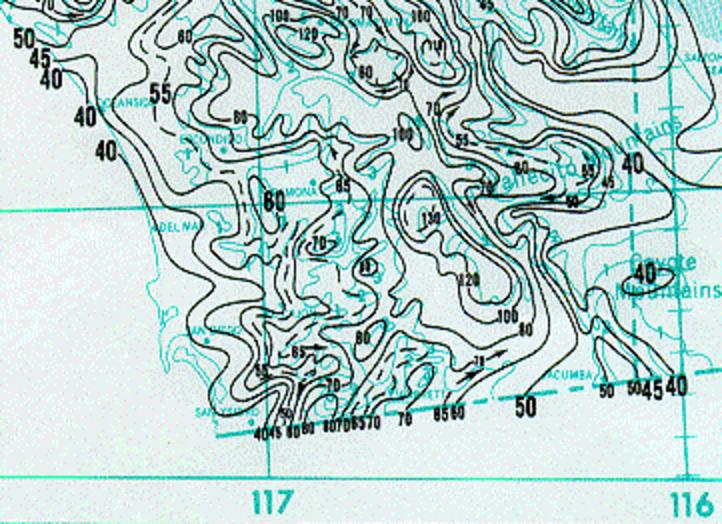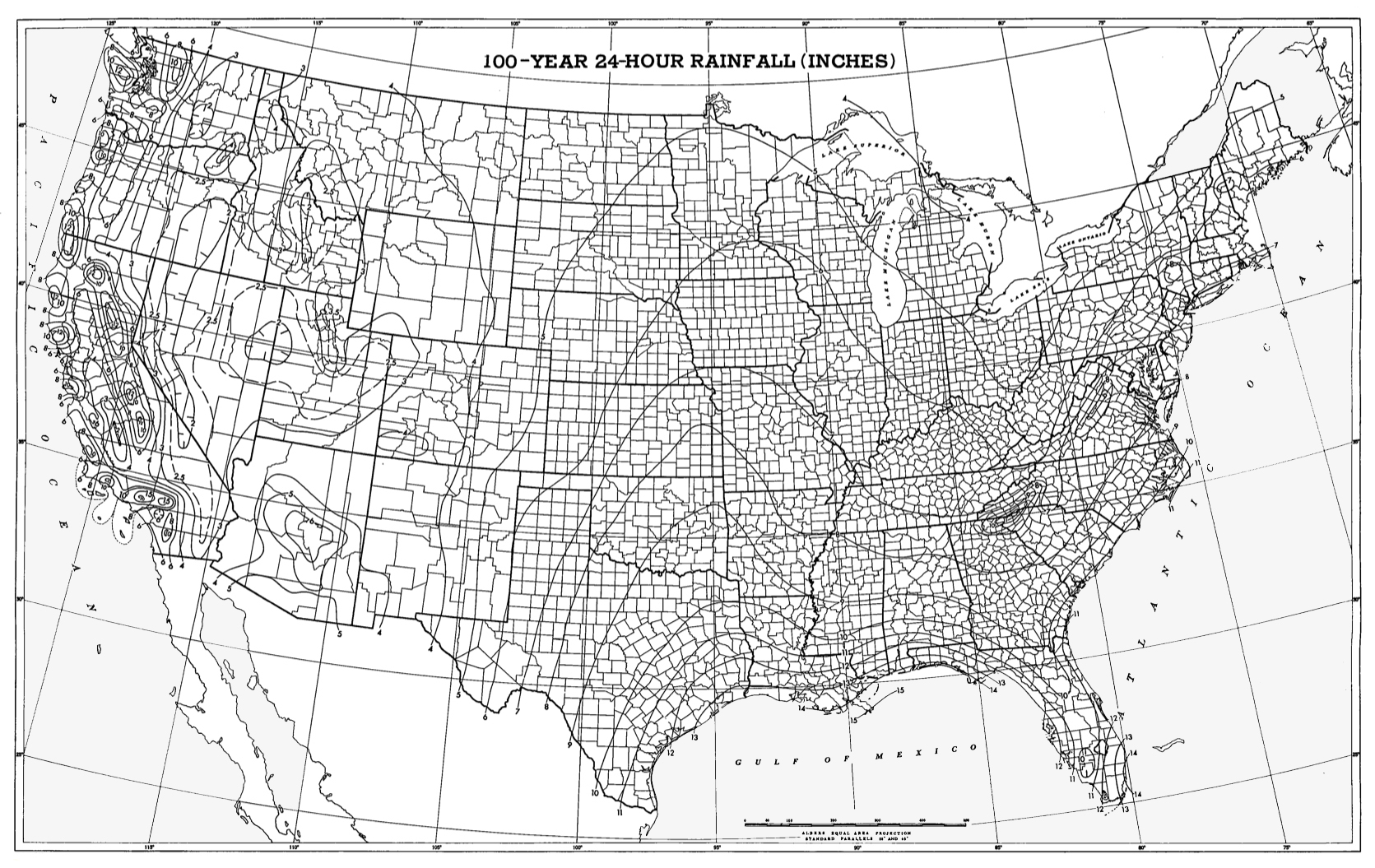Para el mapeo regional de precipitaciones, a las isoyetas se las refiere comúnmente como curvas isopluviales. Mapas de curvas isopluviales correspondientes a los Estados Unidos de América son publicados por el Servicio Meteorológico Nacional [58, 59, 85-88]. Estos mapas muestran curvas de igual profundidad de precipitación, aplicables para un rango de duraciones, frecuencias y ubicaciones geográficas; véase, por ejemplo, la Fig. 2-8 para el condado de San Diego, California, y la Fig. 2-9 para los Estados Unidos, excluyendo Alaska. Fig. 2-8  Curvas isopluviales de 100 años de frecuencia y 24 h de duración, aplicables al Condado de San Diego, California (0.1 pulgadas) (Fuente: NOAA) (Haga clic -aquí- para desplegar). Fig. 2-9  Curvas isopluviales de 100 años de frecuencia y 24 h de duración para los Estados Unidos, excluyendo Alaska (pulgadas) (NOAA) (Haga clic -aquí- para desplegar). En el caso de cuencas mayores, las tormentas muy intensas suelen cubrir solamente una fracción de la cuenca; sin embargo, esto puede causar grandes inundaciones en ciertas zonas. Por lo general, el rol de las tormentas eléctricas en la determinación del potencial de inundación de cuencas mayores es evaluado en forma individual. Precipitación media sobre un área dada. La cantidad de precipitación (o lluvia) se mide con pluviómetros. Durante una tormenta, es probable que la profundidad medida por dos o más pluviómetros del mismo tipo no sea la misma. En el análisis hidrológico a menudo es necesario determinar una media espacial de las precipitaciones sobre una cuenca. Esto se logra con cualquiera de los siguientes métodos: Precipitación media, Polígonos de Thiessen, y Curvas isoyetas. 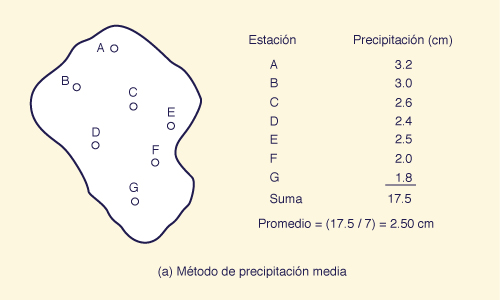En el método de precipitación media, se tabulan las profundidades medidas por los pluviómetros situados dentro de la cuenca de captación. Estas profundidades se promedian para encontrar el valor medio de precipitación, como se muestra en la Fig. 2-10 (a). Fig. 2-10 (a)  Método de precipitación media (Haga clic -aquí- para desplegar). 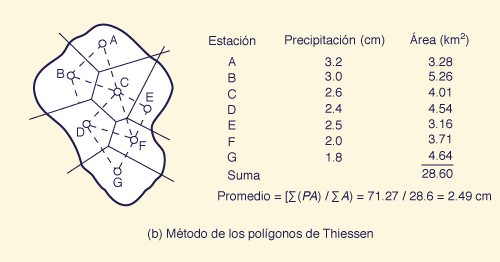En el método de los polígonos de Thiessen, se traza la ubicación de los pluviómetros en un mapa a escala de la cuenca. Las ubicaciones de las estaciones se unen con líneas rectas con el fin de formar un patrón de triángulos (línea punteada en la Fig. 2-10 (b)), preferentemente con lados de aproximadamente la misma longitud. Luego se trazan bisectrices perpendiculares a los lados de estos triángulos para encerrar cada estación dentro de un polígono llamado de Thiessen, el cual circunscribe un área de influencia, como se muestra en la Fig. 2-10 (b). La precipitación media en la cuenca se calcula ponderando la profundidad de lluvia de cada estación en proporción a su área de influencia. Fig. 2-10 (b)  Método de los polígonos de Thiessen (Haga clic -aquí- para desplegar). 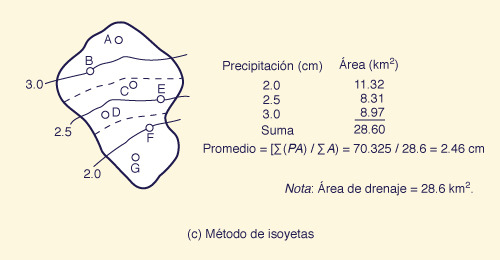En el método de isoyetas, se traza la ubicación de los pluviómetros en un mapa a escala de la cuenca. La profundidad de lluvia en cada estación se utiliza para dibujar isoyetas lo largo de la cuenca, de manera similar a la utilizada en la preparación de las curvas de nivel de mapas topográficos. La mitad de la distancia entre dos isoyetas adyacentes se utiliza para delinear el área de influencia de cada isohyeta, como se muestra en la Fig. 2-10 (c). La precipitación media en la cuenca se calcula ponderando cada isoyeta en proporción a su área de influencia. Fig. 2-10 (c)  Método de isoyetas (Haga clic -aquí- para desplegar). El método de las isoyetas se considera más preciso que los polígonos de Thiessen o la media de precipitaciones. Éste es particularmente el caso cuando los efectos orográficos ejercen una gran influencia en el patrón local de precipitaciones. El método de los polígonos Thiessen es generalmente más exacto que el método de la media de precipitaciones. El aumento en la precisión es probable que sea más marcado cuando las profundidades de lluvia son muy variadas, o cuando existen grandes diferencias en las áreas de influencia. Análisis de tormentas Profundidad y duración de una tormenta. La profundidad y la duración de una tormenta están directamente relacionadas, habiendo un aumento en la profundidad con un aumento de duración. La siguiente ecuación relaciona la profundidad y duración de una tormenta: h = c t n (2-2) en el cual h = profundidad de la tormenta, en centímetros; t = duración de la tormenta, en horas; C = coeficiente; y n = exponente (un número real positivo menor que 1). Típicamente, n varía entre 0.2 y 0.5, lo que indica que la profundidad de tormenta crece a una velocidad menor que la duración. Usando una base de datos regional o local, la Ec. 2-2 se puede utilizar para predecir la profundidad de tormenta en función de la duración. La aplicabilidad de dicha ecuación, sin embargo, se limita a las condiciones regionales o locales para las que se haya derivado. 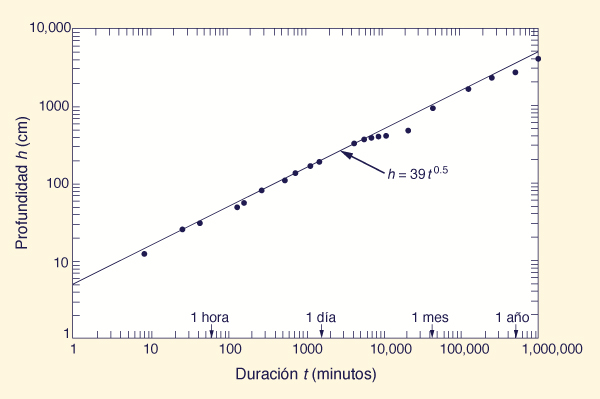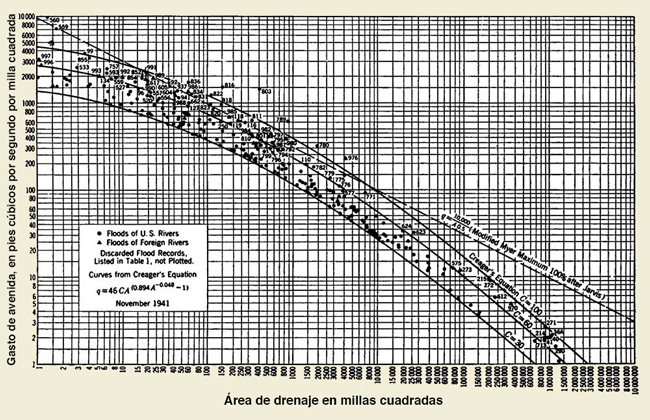La Ec. 2-2 también se puede utilizar para analizar las características de eventos extremos. Una gráfica logarítmica de los datos de profundidad y duración para los mayores eventos observados en el mundo (Tabla 2-2) se traduce en la siguiente línea envolvente: h = 39 t 0.5 (2-3) en el cual h = profundidad de precipitación, en centímetros, y t = duración, en horas. Los datos de la Tabla 2-2 se representan en la Fig. 2.11, incluyendo la línea envolvente, Ec. 2-3. Tabla 2-2   Eventos máximos de precipitación observados en el mundo [53]. Duración Profundidad (cm) Localización Fecha 1 min 3.8 Barot, Guadeloupe 1970 Noviembre 26 8 min 12.6 Fussen, Bavaria 1920 Mayo 25 15 min 19.8 Plumb Point, Jamaica 1916 Mayo 12 42 min 30.5 Holt, Missouri 1947 Junio 22 2 h 10 min 48.3 Rockport, West Virginia 1889 Julio 18 2 h 45 min 55.9 D'Hanis, Texas (17 mi NNW) 1935 Mayo 31 4 h 30 min 78.2 Smethport, Pennsylvania 1942 Julio 18 9 h 108.7 Belouve, Reunion 1964 Febrero 18 12 h 134.0 Belouve, Reunion 1964 Febrero 28-29 18 h 30 min 168.9 Belouve, Reunion 1964 Febrero 28-29 24 h 187.0 Cilaos, Reunion 1952 Marzo 15-16 2 d 250.0 Cilaos, Reunion 1952 Marzo 15-17 3 d 324.0 Cilaos, Reunion 1952 Marzo 15-18 4 d 372.1 Cherrapunji, India 1974 Septiembre 12-15 5 d 385.4 Cilaos, Reunion 1952 Marzo 13-18 6 d 405.5 Cilaos, Reunion 1952 Marzo 13-19 7 d 411.0 Cilaos, Reunion 1952 Marzo 12-19 15 d 479.8 Cherrapunji, India 1931 Junio 24-30 1 m 930.0 Cherrapunji, India 1861 Julio 3 m 1637.0 Cherrapunji, India 1861 Mayo-Julio 6 m 2245.0 Cherrapunji, India 1861 Abril-Septiembre 1 año 2646.0 Cherrapunji, India 1860 Agosto a 1861 Julio 2 años 4077.0 Cherrapunji, India 1860-1861 Fig. 2-11  Profundidad vs duración para grandes eventos de precipitación observados a nivel mundial. Intensidad y duración de tormenta. La intensidad y duración de una tormenta están inversamente relacionadas. A partir de la Ec. 2-2 se puede obtener una ecuación que relaciona intensidad y duración, diferenciando la profundidad de lluvia con respecto a la duración, lo cual lleva a lo siguiente:   dh _____  = i = c n t n -1   dt (2-4) en la cual i = intensidad de tormenta. Simplificando:          a i =  ______          t m (2-5) en la cual a = cn, y m = 1 - n. Dado que n es menor que 1, se deduce que m es también menor que 1. Otro modelo de intensidad-duración es el siguiente:            a i =  ________          t + b (2-6) en la cual a y b son constantes a ser determinadas por medio de un análisis de regresión (Capítulo 7). Un modelo de intensidad-duración que combina las características de las Ecs. 2-5 y 2-6 es el siguiente:                a i =  _____________          ( t + b ) m (2-7) Para b = 0, la Ec. 2-7 se reduce a la Ec. 2-5; para m = 1, la Ec. 2-7 se reduce a la Ec. 2-6. 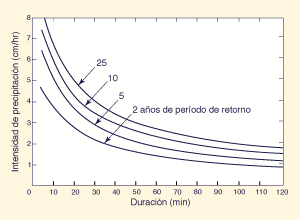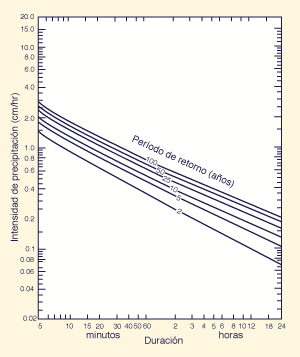Intensidad-Duración-Frecuencia. Para cuencas pequeñas, es necesario determinar varias curvas de intensidad-duración, aplicables a frecuencias (o períodos de retorno) diferentes. Al conjunto de curvas de intensidad-duración-frecuencia se le conoce como las curvas IDF, con la duración ploteada en las abscisas, la intensidad en las ordenadas, y la frecuencia (o período de retorno) como el parámetro de la curva. La escala utilizada en la construcción de las curvas IDF es aritmética [Fig. 2-12 (a)] o logarítmica [Fig. 2-12 (b)]. Estas curvas son desarrollados por organismos oficiales para su uso en el diseño de obras de drenaje urbano y aplicaciones similares (Capítulo 4). Se puede obtener una fórmula para la curva IDF suponiendo que la constante a en las Ecs. 2-5 a 2- 7 está relacionada con el período de retorno T de la siguiente manera: a = k T n (2-8) en la cual k = un coeficiente; T = período de retorno; y n = un exponente (no relacionado con el n de la Ec. 2-2). Esto lleva a lo siguiente:               k T n i =  _____________          ( t + b ) m (2-9) Los valores de k, b, m, n y se evalúan a partir de datos medidos o experiencia local. Fig. 2-12 (a)  Una curva IDF aritmética (Davenport, Iowa) [84].    Fig. 2-12 (b)  Una curva IDF logarítmica (San José, California) [84]. 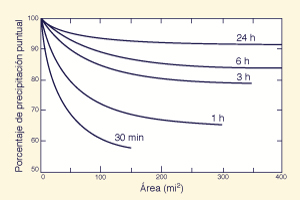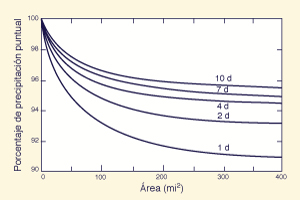Relación entre la profundidad de tormenta y el área de la cuenca. Generalmente, cuanto mayor sea el área de la cuenca, menor será el promedio espacial de la profundidad de tormenta. Esta variación de la profundidad de tormenta con el área de cuenca ha llevado al concepto de profundidad puntual, definida como la profundidad de tormenta asociada con un área puntual dada. Un área puntual es el área más pequeña por debajo de la cual la variación de la profundidad de tormenta con el área de cuenca puede ser desestimada. El tamaño del área puntual se toma generalmente como 25 km2 (10 mi2). La profundidad puntual se aplica para todas las áreas menores que el área puntual. Para áreas mayores que el área puntual, se hace necesaria una reducción en la profundidad de tormenta, teniendo en cuenta la disminución de profundidad con el área de cuenca. Esta reducción se lleva a cabo usando un gráfico de reducción de profundidad-área, el cual relaciona el área de la cuenca (en las abscisas) con un porcentaje de la profundidad puntual (en las ordenadas). La duración de la tormenta suele ser un parámetro de curva en un gráfico de reducción de este tipo. 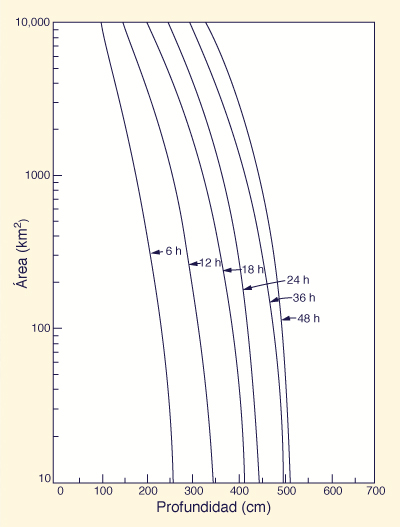El Servicio Meteorológico Nacional (EE.UU.) ha publicado gráficos generalizados de reducción de profundidad-área, aplicables a los Estados Unidos, para áreas de hasta 1,000 km2 (400 mi2) y duraciones desde 30 minutos hasta 10 días [Fig. 2.13 (a) y (b)]. Los gráficos regionales y locales pueden diferir de estos gráficos (véase la Sección 14.1). Fig. 2-13 (a)   Reducción generalizada de profundidad puntual para tormentas de duración de 30 minutos a 24 horas.    Fig. 2-13 (b)  Reducción generalizada de profundidad puntual para tormentas de duración de 1 a 10 días. Profundidad-Duración-Frecuencia. Para cuencas de tamaño medio, el enfoque del análisis hidrológico cambia de la intensidad a la profundidad. Los mapas isopluviales, disponibles para todos los Estados Unidos de América, representan profundidades de tormenta aplicables a una serie de duraciones, frecuencias y áreas de cuenca [58, 59, 85-88]. Estos mapas muestran valores de profundidad puntual; por lo tanto están sujetos a la reducción de profundidad-área mediante el uso de un gráfico apropiado. Profundidad-Area-Duración. Otra forma de describir la relación entre la profundidad y duración de una tormenta y el área de la cuenca es la técnica conocida como profundidad-área-duración (PAD). Ésta es básicamente una forma alternativa de representar la reducción de la profundidad de tormenta con el área, con la duración como tercera variable. Para construir un gráfico PAD, se identifica un evento que tiene un único ojo de tormenta, como se muestra en la Fig. 2-6 (b). Se preparan mapas de isoyetas, mostrando profundidades máximas de tormenta para varias duraciones típicas (6-h, 12-h, 24-h, etc.). Para cada mapa, las isoyetas se toman como límites que circunscriben áreas específicas. Para cada mapa y cada área, se calcula una profundidad de precipitación espacialmente promediada dividiendo el volumen total por el área. Este procedimiento proporciona un conjunto de datos PAD utilizados para construir un gráfico que muestra el área versus la profundidad, con la duración como parámetro de la curva (Fig. 2-14). Fig. 2-14  Una curva de profundidad-área-duración (PAD). El análisis PAD también puede ser utilizado para estudiar las características regionales de precipitación. La Tabla 2-3 muestra los datos máximos para los Estados Unidos, basado en cuatro eventos extremos. Los datos confirman que la profundidad de tormenta aumenta con la duración y disminuye con el área de la cuenca. Tabla 2-3   Tabla 2-3  Datos máximos de profundidad-área-duración para los Estados Unidos [76]. * Area (km2) Duración (h) 6 12 18 24 36 48 72 25 62.7a 75.7b 92.2c 98.3c 106.2c 109.5c 114.8c 250 49.8b 66.8c 82.5c 89.4c 96.3c 98.8c 103.1c 500 45.5b 65.0c 79.8c 86.9c 93.2c 95.8c 99.6c 1250 39.1b 62.5c 75.4c 83.0c 88.9c 91.4c 94.7c 2500 34.0b 57.4c 69.6c 76.7c 83.6c 85.6c 88.6c 5000 28.4b 45.0c 57.1c 63.0c 69.3c 72.1c 75.4c 12500 20.6b 28.2b 35.8b 39.4c 47.5d 52.6d 62.0d Tormenta:  a.  Julio 17-18, 1942, Smethport, Pennsylvania; b.  Septiembre 8-10, 1921, Thrall, Texas; c.  Septiembre 3-7, 1950, Yankeetown, Florida; d.  Junio 27-Julio 1, 1899, Hearne, Texas. *  Profundidad media en cm; la tormenta está indicada por el superíndice. Precipitación Máxima Probable. Para proyectos de gran envergadura, el análisis de tormentas a partir de datos de profundidad-duración-frecuencia no es suficiente para eliminar la probabilidad de falla. En tales casos, el concepto de Precipitación Máxima Probable (PMP) se utiliza en su lugar. En los Estados Unidos, las estimaciones de PMP se desarrollan siguiendo pautas incluídas en la serie de informes hidrometeorológicos HM NOAA [33-44] y publicaciones relacionadas [84-87]. Estos informes contienen metodologías y mapas para la estimación de PMP para una ubicación geográfica determinada, rango de duraciones, áreas de cuenca, y estación prevaleciente (Capítulo 14). Variaciones geográficas y estacionales de precipitación La precipitación varía no sólo temporal y espacialmente, sino también estacionalmente, anualmente y con la ubicación geográfica y el clima regional o local. La precipitación media anual, es decir, la cantidad total de precipitación que se acumula en un año, en promedio, en un lugar determinado, se usa para clasificar los climas en ocho clases (en términos de precipitación) [11]: Superárido: Menos de 100 mm Hiperárido: 100 - 200 mm Árido: 200 - 400 mm Semiárido: 400 - 800 mm Subhúmedo: 800 - 1600 mm Húmedo: 1600 - 3200 mm Hiperhúmedo: 3200 - 6400 mm Superhúmedo: Más de 6.400 mm La estacionalidad de la precipitación se evalúa con el índice de estacionalidad, definido como la relación entre la precipitación acumulada en los tres meses consecutivos más húmedos a la de los tres meses consecutivos más secos, en un año promedio. Este índice se utiliza para clasificar los climas en cuatro clases [11]: No estacional:  1.0 - 1.6 Débilmente estacional:  1.6 - 2.5 Moderadamente estacional: 2.5 - 10.0 Fuertemente estacional: Mayor de 10. En general, los climas áridos y semiáridos están asociados con los regímenes moderadamente estacionales; por el contrario, los climas subhúmedos y húmedos están asociados con regímenes débilmente estacionales o no estacionales. Sin embargo hay algunas excepciones; por ejemplo, el caso de los climas de tipo monzón que prevalecen en algunas partes del mundo, los cuales tienden a ser a la vez húmedos y estacionales. Fuentes de datos de precipitación Los datos de precipitación se obtienen por medición mediante el uso de pluviómetros (Capítulo 3). El Centro Nacional de Datos Climáticos (CNDC), ubicado en Asheville, Carolina del Norte, EE.UU., publica datos de precipitación para cerca de 8,000 estaciones. Otras agencias federales, estatales y locales, además de personas individuales, operan un gran número de pluviómetros adicionales. Las agencias federales que colectan datos de precipitación en forma regular incluyen el Servicio Meteorológico Nacional (SMN), el Cuerpo de Ingenieros del Ejército, el Servicio de Conservación de Recursos Naturales, el Servicio Forestal, el Bureau of Reclamation, y la Autoridad del Valle de Tennessee. El CNDC colecta datos de precipitación usando intervalos de hora, dia, mes y año. Datos de precipitación horaria y máximas cantidades en 15 minutos de duración se encuentran en Hourly Precipitation Data. Datos de precipitación diaria y mensual se encuentran en Climatological Data. Datos de precipitación mensual y anual de unas 250 ciudades principales de EE.UU., incluyendo las velocidades por hora, se encuentran en Local Climatological Data. Los atlas regionales de precipitación (US Weather Bureau No 40 [86], Memorandum Técnico de NOAA NWS Hydro-35 [59] y Atlas de Precipitación-Frecuencia del Oeste de los Estados Unidos [58]) están disponibles. Los mapas de precipitaciones mensuales y estacionales se encuentran en el Weekly Weather and Crop Bulletin, disponible en NOAA/USDA Joint Agricultural Weather Facility, Washington, D.C. Otras fuentes de datos de precipitación se encuentran en la Bibliografía Anotada de Publicaciones de Interés Hidrometeorológico, actualizada periódicamente por SMN (NWS), y en la Guía Selectiva para Fuentes de Datos Climáticos, actualizada periódicamente por CNDC. Datos de precipitación y otros datos climatológicos están disponibles en línea a través del sitio web del CNDC (http://www.ncdc.noaa.gov). Al hacer clic en On-line Data Access se provée el acceso a una serie de servicios, incluyendo: (1) precipitación mensual en los Estados Unidos, y (2) On-line Access and Service Information System (OASIS), que contiene precipitación horaria y de 15 minutos de duración. Llenado de registros faltantes. A veces se tiene un registro incompleto de precipitaciones debido a un error del operador o a un mal funcionamiento del equipo. En este caso, a menudo es necesario estimar el registro faltante. Asumir que una determinada estación X tiene un registro faltante. Un procedimiento para rellenar el registro faltante es identificar tres estaciones de índice (A, B y C) que poseen registros completos, ubicadas lo más cerca posible y lo más uniformemente espaciadas alrededor de la estación X. Se evalúa la precipitación media anual para cada una de las estaciones (X, A, B y C). Si la precipitación media anual en cada una de las estaciones de índice A, B, o C está dentro del 10 por ciento de aquélla de la estación X, una media aritmética simple de los valores de las precipitaciones en las estaciones índice proporciona el valor faltante en la estación X. El método de razón normal se utiliza si la precipitación media anual en cualquiera de las estaciones de índice difiere en más del 10% de aquélla de la estación X [55]. En este caso, el valor faltante en la estación X se estima de la siguiente manera:                         NX               NX               NX PX =  (1/3)   [ _____ PA  +  _____ PB  +  _____ PC ]                         NA               NB               NC (2-10) en la cual P = precipitación, N = precipitación media anual, y los subíndices X, A, B, y C se refieren a las respectivas estaciones. El Servicio Meteorológico Nacional ha desarrollado un método alternativo para rellenar datos faltantes de precipitación [49]. 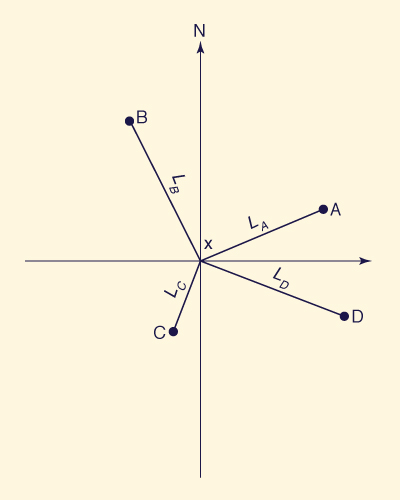El método requiere de datos para cuatro estaciones índice A, B, C, y D, situadas cada una lo más cerca posible de la estación X de interés, y ubicadas en cada uno de los cuatro cuadrantes delimitados por líneas norte-sur y este-oeste trazadas sobre la estación X (Fig. 2-15). El valor estimado de la precipitación en la estación X es la media ponderada de los valores en los cuatro lugares índice. Para cada estación índice, el peso aplicable es el inverso del cuadrado de la distancia L de la respectiva estación índice a la estación X. Fig. 2-15   Posición relative de la estación X y las estaciones índice A, B, C y D. El procedimiento se describe por la siguiente fórmula:               4              Σ ( Pi / Li 2 )                i = 1 PX =  _____________________                  4                 Σ ( 1 / Li 2 )             i = 1 (2-11) en la cual P = precipitación; L = distancia entre las estaciones índice y la estación X; e i se refiere a cada una de las estaciones índice A, B, C y D. 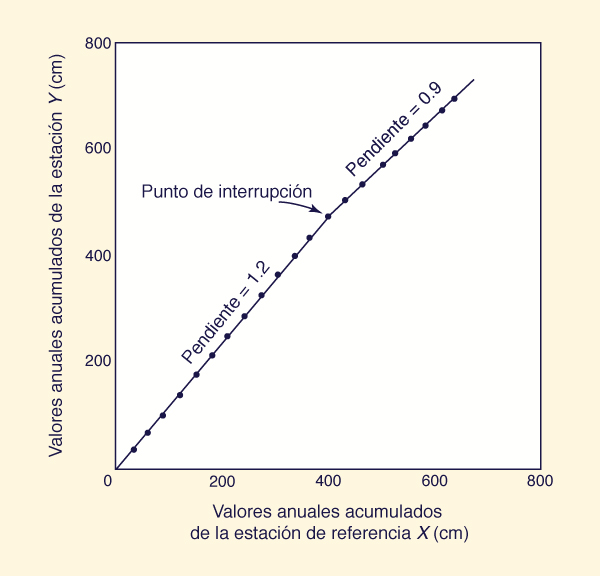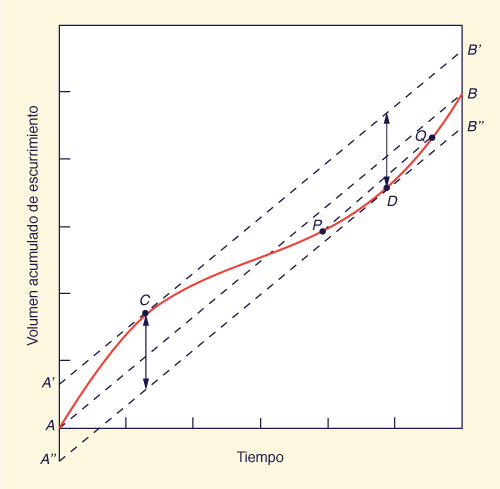Diagrama de doble masa. Los cambios en la ubicación o exposición de un pluviómetro pueden tener un efecto apreciable en la cantidad de precipitación medida, lo que produce datos inconsistentes, es decir, datos de diferente naturaleza dentro de un mismo registro. El diagrama de doble masa se usa para analizar la consistencia de un registro de precipitaciones. El método compara los valores cumulativos anuales (o, alternativamente, estacionales) de la estación Y con las de una estación de referencia X. El dato de la estación de referencia es por lo general el promedio de varias estaciones vecinas. Los pares cumulativos (o valores de doble masa) se grafican en un sistema de coordenadas aritmética x-y, y la gráfica se examina buscando cambios de tendencia en doble masa. Si la gráfica es esencialmente lineal, el registro en la estación Y es consistente. De otro modo, si la gráfica muestra un cambio en la pendiente, el registro de la estación Y es inconsistente. La corrección se realiza mediante el ajuste de los registros antes del cambio para reflejar el nuevo estado, después de cambio de pendiente. Para esto, los registros de lluvia (antes del cambio de pendiente) se multiplican por la razón de las pendientes después y antes del cambio, como se indica en la Fig. 2-16. Fig. 2-16  Diagrama de doble masa. 2.2  ABSTRACCIONES HIDROLÓGICAS [Características de la Cuenca]   [Escurrimiento]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Precipitación]   Las abstracciones hídrológicas son procesos que actúan con el fin de convertir la precipitación total en precipitación efectiva. Esta última es la que eventualmente produce el escurrimiento, o escorrentía. La diferencia entre la precipitación total y la precipitación efectiva es la profundidad abstraída por la cuenca. Son varios los procesos por medio de los cuales las precipitaciones se abstraen de una cuenca. Aquéllos de importancia en la ingeniería hidrológica son: Intercepción; Infiltración; Almacenamiento de superficie, o en una depresión natural or artificial del terreno; Evaporación; y Evapotranspiración. Intercepción La intercepción es el proceso por medio del cual la precipitación es abstraída por la vegetación u otras formas de cobertura del paisaje, incluyendo, en algunos casos, las características culturales. En general, la intercepción es la fracción de precipitación que es retenida por la cubierta vegetal. La cantidad interceptada, o bien retorna eventualmente a la atmósfera por evaporación, o constituye el escurrimiento demorado, es decir, la fracción de la precipitación que llega al terreno pasando primero en forma rápida por la cubierta vegetal. Las pérdidas por intercepción son una función de: Las características de la tormenta, incluyendo intensidad, profundidad, y duración, El tipo, especie, edad, y densidad de la cubierta vegetal, y La estación del año. La intercepción suele ser el primer proceso de abstracción actuante durante una tormenta. Las tormentas suaves, las cuales ocurren frecuentemente, tienden a ser casi totalmente abstraídas por el proceso de intercepción. La pérdidas anuales por intercepción, principalmente asociadas con tormentas suaves, ascienden a alrededor de 25 por ciento de la precipitación media anual. Para tormentas moderadas, las pérdidas por intercepción tienden a variar grandemente, siendo mayores durante la estación de crecimiento y menores en otras épocas del año. Los estudios han demostrado que los valores de intercepción tienden a variar de 7 al 36 por ciento de la precipitación total durante la estación de crecimiento, y del 3 al 22 por ciento durante el resto del año [12]. Para tormentas fuertes, las pérdidas por intercepción son generalmente una pequeña fracción de la precipitación total. Para tormentas de larga duración o poco frecuentes, es muy probable que el efecto de intercepción sea pequeño. En ciertos casos, en particular para los estudios de hidrología de inundaciones, es justificable el despreciar la intercepción por motivos prácticos. La pérdida por intercepción comprende dos componentes distintos [25]. El primero es el almacenamiento (de intercepción), es decir, la profundidad (o volumen) retenidos en el follaje contra las fuerzas del viento y gravedad. El segundo es la pérdida por evaporación (de la superficie del follaje), que tiene lugar durante la duración de la tormenta. La combinación de estos dos procesos conduce a la siguiente fórmula para estimar intercepción [12]: L =  S + K E t (2-12) en la cual L = pérdida por intercepción, en milímetros; S = almacenamiento de intercepción, en milímetros, que por lo general varía de 0.25 a 1.25 mm; K = relación entre la superficie de evaporación del follaje y su proyección horizontal; E = velocidad de evaporación, en milímetros por hora; y t = duración de la tormenta, en horas. Infiltración La infiltración es el proceso por medio del cual la precipitación se introduce en el suelo. Una vez allí, el flujo es principalmente en dirección vertical hacia los acuíferos subyacentes, y luego, en forma casi horizontal, hacia lagos, arroyos, y ríos cercanos. El agua que llega a los lagos, o bien se evapora, o drena como desbordamiento hacia corrientes superficiales vecinas. El agua que llega a los arroyos y ríos se mueve con relativa rapidez hacia los océanos, constituyendo el flujo superficial. El agua de los acuíferos se mueve lentamente a medida que el flujo de las aguas subterráneas fluye hasta llegar a los ríos, constituyendo el flujo base de las agua superficiales, o hasta llegar directamente al mar, evitando las aguas superficiales. La infiltración es un proceso complejo; se describe ya sea por una velocidad instantánea o por una velocidad media, en milímetros por hora o pulgadas por hora. La profundidad total de infiltración se obtiene integrando la velocidad de infiltración instantánea a través de la duración de la tormenta. La velocidad de infiltración media se obtiene dividiendo la profundidad total de infiltración entre la duración de la tormenta. La velocidad de infiltración es función de los siguientes factores: La condición de la superficie, incluyendo el grado de compactación y la posible formación de costras superficiales; El tipo y densidad de la cubierta vegetal y la estructura radicular asociada; Las propiedades físicas del suelo, incluyendo estructura, tamaño del grano o partícula, y gradación; Las características de la tormenta, es decir, intensidad, profundidad, y duración; La temperatura del agua; y La calidad del agua, incluyendo componentes químicos y otras impurezas. 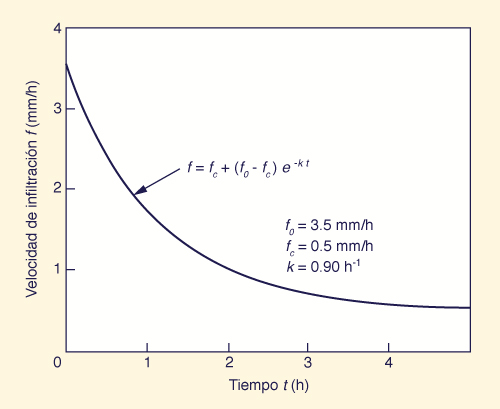Fórmulas de infiltración. Para una tormenta dada, la velocidad de infiltración tiende a variar en función el tiempo. La velocidad de infiltración inicial es el valor aplicable al comienzo de la tormenta. Es probable que esta velocidad sea la máxima, disminuyendo gradualmente a medida que progresa la tormenta. Para tormentas de larga duración, la velocidad final de infiltración alcanza un valor constante, al cual se refiere como la velocidad de infiltración final o de equilibrio. Este proceso dio lugar a que Horton [27] describiera la variación de la velocidad de infiltración mediante la siguiente fórmula: f = fc + ( fo - fc ) e-k t (2-13) en el cual f = velocidad de infiltración instantánea; fo = velocidad de infiltración inicial; fc = velocidad de infiltración final; k = constante de decaimiento exponencial; y t = tiempo, en horas. Las unidades de k are h-1. Para t = 0, f = fo; y para t = ∞, f = fc (véase la Fig. 2-17). Fig. 2-17   Fórmula de infiltración de Horton. La Ecuación 2.13 tiene tres parámetros: (1) la velocidad de infiltración inicial fo; (2) la velocidad de infiltración final fc; y (3) el valor de k que describe el decaimiento de la diferencia entre las velocidades de infiltración iniciales y finales. Son necesarias mediciones de campo a fin de determinar los valores adecuados de estos parámetros. Un gráfico de la velocidad de infiltración en función del tiempo permite la estimación de la velocidad final fc . Conociendo la velocidad final, se obtienen dos pares de f y t del gráfico y se utilizan, junto con la Ec. 2-13, para obtener fo y k. La integración de la Ec. 2-13 entre t = 0 y t = ∞ lleva a lo siguiente:           fo - fc F =  ________              k (2-14) en la cual F = la profundidad total de infiltración por encima de la línea f = fc. La Ec. 2-14 permite el cálculo de la profundidad total de infiltración, asumiendo que la tormenta dura el tiempo suficiente para que se alcance la velocidad final, o de equilibrio. Ejemplo 2-2. Asumiendo fo = 10 mm/h, fc = 5 mm/h, y k = 0.95 h-1, c&lcular de la profundidad total de infiltración para una tormenta de 6 h. Después de 6 h, la diferencia entre la tasas instantánea y final es despreciable. Por lo tanto, la profundidad total de infiltración es: (10 mm/h - 5 mm/h) / 0.95 h-1 + (5 mm/h × 6 h) = 35.26 mm. La Tabla 2-4 muestra velocidades de infiltración típicas al final de 1 h (f1). Generalmente, estos valores son aproximaciones razonables de las velocidades de infiltración finales, o de equilibrio. Tabla 2-4   Valores típicos de f1 [1]. Tipo de suelo Velocidad de infiltración f1 (mm/h) Arcillas, franco arcilloso Bajo 0.25-2.50 Margas, arcillas, limos Intermedio 2.50-12.50 Suelos arenosos Alto 12.50-25.00 Desarrollos más recientes en la teoría de infiltración han tratado de mejorar el modelo de Horton. Philip [66] ha propuesto el siguiente modelo: f = 0.5 s t -1/2 + A (2-15) en el cual f = velocidad de infiltración instantánea; s = un parámetro empírico relacionado con la velocidad de penetración del frente de humectación (la superficie de humectación que se caracteriza por un muy alto gradiente de potencial); A = un valor de velocidad de infiltración que está cerca del valor de conductividad hidráulica saturada en la superficie; y t = tiempo. En la Ec. 2-15, para t = 0, f = ∞; y para t = ∞, f = A. En la práctica, la tasa de infiltración inicial tiene un valor finito. A pesar de esta limitación, la fórmula de Philip parece ser un buen ajuste a los datos experimentales. La integración de la ecuación conduce a: F = s t 1/2 + A t (2-16) en la cual F = profundidad total de infiltración. Un modelo de infiltración con una sólida base teórica es la fórmula de Green y Ampt [21]. Esta ecuación describe la velocidad de infiltración de la siguiente manera:                        H + Pf               f =  K   ( 1 +  _________ )                           Zf               (2-17) en la cual f = velocidad de infiltración, en milímetros por hora; K = conductividad hidráulica saturada, en milímetros por hora; H = profundidad del agua estancada, en milímetros; Pf = presión capilar en el frente de humectación, en milímetros; y Zf = profundidad vertical de la zona saturada, en milímetros. En la práctica, sin embargo, puede ser difícil medir algunos de los términos de esta ecuación. Se ha obtenido algún progreso agrupando términos de la Ec. 2-17 en parámetros determinables relacionados con los procesos físicos [48]. Índices de infiltración. En la práctica, las evaluaciones de infiltración se han visto obstaculizadas por su inherente variabilidad espacial y temporal. Esto ha llevado a la utilización de los índices de infiltración, los cuales modelan el proceso de infiltración de una manera aproximada pero práctica. Los índices de infiltración asumen que la velocidad de infiltración es constante durante toda la duración de la tormenta. Este supuesto tiende a subestimar la velocidad inicial de infiltración y a sobreestimar la velocidad final. Por esta razón, los índices de infiltración son más adecuados para aplicaciones con tormentas de larga duración, o cuencas con alto contenido de humedad inicial. Bajo tales condiciones, el supuesto de una velocidad de infiltración constante en el tiempo es usualmente justificado por motivos prácticos. Para tormentas moderadas, el uso de índices de infiltración es en gran parte un procedimiento empírico. En este caso, la atención se centra en encontrar la condición de humedad del suelo y duración de tormenta que haga posible un balance adecuado de las cantidades de lluvia y escurrimiento. 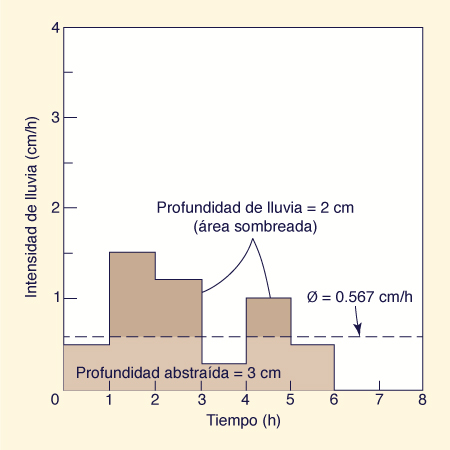En la práctica, el índice de infiltración más utilizado es el índice φ, definido como la velocidad de infiltración [un valor constante] que hay que restar de la intensidad de lluvia con el fin de obtener el volumen de escurrimiento que actualmente ocurrió [13]. El cálculo del índice φ requiere un patrón de tormenta dado, es decir, un gráfico de la variación de la intensidad de lluvia con el tiempo, y un volumen [o profundidad] medido de escurrimiento. El procedimiento de cálculo es iterativo, de prueba y error. Ejemplo 2-3. La siguiente distribución de precipitaciones fue medida durante una tormenta de 6 h de duración: Tiempo (h) 1 2 3 4 5 6 Intensidad de lluvia (cm/h) 0.5 1.5 1.2 0.3 1.0 0.5 La profundidad de escurrimiento se ha estimado en 2 cm. Calcular el índice φ. A partir de la distribución de la lluvia, la precipitación total es de 5 cm. Por lo tanto, la profundidad abstraída por la infiltración es: (5 - 2) = 3 cm. Con referencia a la Fig. 2-18, el índice φ se calcula por prueba y error. Por inspección, se asume un valor inicial de φ entre 0.5 y 1.0 cm/h. Un balance de masa conduce a: [ (1.5 - φ) × 1 ]  +  [ (1.2 - φ) × 1 ]  +  [ (1.0 - φ) × 1 ] = 2 cm (2-18) En la Ec. 2-18, resolviendo para φ da: φ = 0.567 cm/h, verificándose que el rango asumido inicialmente estaba correcto. Si el rango asumido hubiera estado errado, el valor de φ calculado habría estado fuera de ese rango. En la Fig. 2-18, los 2 cm de escorrentía están por encima de la línea que indica el índice φ; y los 3 cm de lluvia abstraída está por debajo. Fig. 2-18  Cálculo de índice φ:  Ejemplo 2-3. Otro índice de infiltración ampliamente utilizado es el índice W [13], el cual, a diferencia del índice φ, toma en cuenta explícitamente la pérdida por intercepción y almacenamiento de superficie. La fórmula para el índice W es la siguiente:             P - Q - S W =  _____________                   tf (2-18) en la que W = índice W, en milímetros por hora; P = altura de lluvia, en milímetros; Q = profundidad de escorrentía, en milímetros; S = la suma de la pérdida por intercepción y almacenamiento superficial, en milímetros; y tf = el tiempo total (horas) durante el cual la intensidad de lluvia es mayor que W. El índice Wmin es el índice W calculado para condiciones extremadamente húmedas. Este índice se deriva a partir de datos correspndientes a la última de una serie de tormentas, y se utiliza en la estimación del máximo potencial de inundación. En resumen, el índice Wmin aproxima a una media espacial de la velocidad de infiltración final. Para tales condiciones extremas, los valores de Wmin y φ son casi idénticos. Infiltración basada en lluvia-escurrimiento. Las fórmulas de inflltration representan la variación de las velocidades de infiltración en el tiempo. Sin embargo, cabe indicar que las velocidades de infiltración varían no sólo en el tiempo, sino también en el espacio. A menos que las mediciones de campo y la correspondiente estimación de parámetros sean bastante bien representativos de la variabilidad espacial, es probable que las velocidades calculadas por las fórmulas de infiltración sean muy diferentes a la realidad. Esta dificultad se evita mediante el cálculo de las velocidades de infiltración en forma indirecta, en base a mediciones de lluvia-escurrimiento. Este tipo de cálculo resulta en un promedio temporal y espacial de la velocidad de infiltración, lo cual equivale a un índice φ, con sus correspondientes ventajas y desventajas. Infiltración y tamaño de la cuenca. Para cuencas medianas y grandes, la variabilidad natural de la velocidad de infiltración hace necesaria la evaluación de la profundidad total de infiltración. En la práctica, la profundidad total de infiltración se deriva del análisis de lluvia-escurrimiento. Sin embargo, cabe notar que para cada aplicación, el cálculo es altamente dependiente del nivel de humedad antecedente del suelo, previo a la tormenta. Al nivel de humedad antecedente de una cuenca se lo conoce como la condición de humedad antecedente, o CHA (Capítulo 5). La velocidad inicial de infiltración y, por consiguiente, la profundidad total de infiltración es una función de la condición de humedad antecedente que prevalece en la zona. Almacenamiento de superficie o en depresiones El almacenamiento de superficie o en depresiones es el proceso por el cual la precipitación es abstraída al ser retenida en charcos, zanjas y otras depresiones naturales o artificiales del terreno. El agua retenida en depresiones, o bien se evapora, o eventualmente contribuye a la humedad del suelo por infiltración. Cabe notar que la inherente variabilidad espacial del almacenamiento de superficie dificulta un cálculo preciso. Intuitivamente, cuanto menor es la pendiente de la cuenca, mayor es el efecto del almacenamiento superficial. Los datos de campo reportados por Viessman [82] demuestran en forma concluyente que el almacenamiento de superficie es inversamente proporcional a la pendiente de la cuenca. Generalmente, la experiencia local puede ser usada para estimar una profundidad equivalente de almacenamiento de superficie. Por ejemplo, Hicks [23] ha utilizado profundidades de almacenamiento de 5.0, 3.75 y 2.5 mm para arena, limo y arcilla, respectivamente. Tholin y Keife [77] han utilizado los valores de 6.25 mm en zonas urbanas permeables y 1.5 mm para áreas pavimentadas. Donde las estimaciones precisas sean difíciles, el almacenamiento de superficie puede ser incluido como parte de otras abstracciones hidrológicas más facilmente determinables, como son la intercepción o infiltración. Una forma alternativa de tomar en cuenta el almacenamiento de superficie es el uso de un factor de corrección de flujo máximo, como se ilustra en el método gráfico NRCS TR-55 (Sección 5.3). Típicamente, el efecto del almacenamiento de superficie varía en el tiempo y, por consiguiente, con la duración de la tormenta. Al comienzo de la tormenta, el almacenamiento de superficie usualmente juega un papel preponderante en la abstracción de la precipitación. Sin embargo, conforme pasa el tiempo, los volúmenes de almacenamiento de superficie son totalmente satisfechos, con cualquier volumen adicional de agua pasando a formar parte del escurrimiento. Esta realidad ha llevado al siguiente modelo conceptual de almacenamiento de superficie: Vs = Sd ( 1 - e - k Pe ) (2-19) en la cual Vs = profundidad equivalente de almacenamiento de superficie o en depresiones, en milímetros; Pe = precipitación efectiva, igual a la precipitación menos la intercepción menos la infiltración, en milímetros; Sd = capacidad total de almacenamiento de superficie y en depresiones, en milímetros; y k = una constante. Linsley et al. [53] han sugerido que los valores de Sd para la mayoría de las cuencas están dentro el rango de 10 a 50 mm. El valor de la constante k se estima suponiendo que para valores muy pequeños de precipitación efectiva (Pe ≅ 0), esencialmente toda la precipitación es tomada por el almacenamiento de superficie (dVs / dPe = 1). Por lo tanto, el valor de la constante k es: k = 1/Sd . Evaporación La evaporación es el proceso por medio del cual el agua acumulada en la superficie de la Tierra (incluídos el agua retenida en depresiones superficiales y los cuerpos mayores de agua, como lagos y embalses) se convierte a estado de vapor y regresa a la atmósfera. La evaporación se produce en la superficie de evaporación, es decir, el contacto entre el cuerpo de agua y el aire suprayacente. En la superficie de evaporación existe un intercambio contínuo de moléculas de agua líquida a vapor de agua, y viceversa. La evaporación se refiere a la tasa neta de transferencia de agua del estado líquido al estado de vapor. La evaporación se expresa como una velocidad de evaporación, en milímetros por día (mm/día), centímetros por día (cm/d), o pulgadas por día (pulg/día). La velocidad de evaporación es función de varios factores meteorológicos y ambientales, entre los cuales los más importantes son: Radiación solar neta, Presión de vapor de saturación, Presión de vapor del aire, Temperaturas del aire y de la superficie del agua, Velocidad del viento, y Presión atmosférica. Cabe mencionar que las tasas de evaporación están significativamente afectadas por el clima. 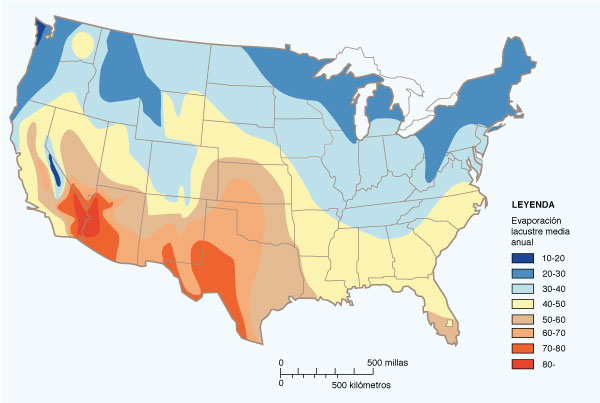Los estudios han demostrado que las tasas de evaporación son altas en regiones áridas y semiáridas, y bajas en regiones húmedas. Por ejemplo, la media de la evaporación anual (de lagos) en los Estados Unidos varía de 20 pulg. (508 mm) en las esquinas Noreste (Maine) y Noroeste (estado de Washington), a más de 80 pulg. (2184 mm) en el desierto del sudoeste (California y Arizona) (Fig. 2-19) [18]. Fig. 2-19  Evaporación anual de lagos en los Estados Unidos de América (NOAA). El efecto del clima en la evaporación tiene un impacto considerable en el desarrollo de los recursos hídricos. La planificación y el diseño de embalses en regiones áridas y semiáridas requiere de una evaluación detallada de la tasa de evaporación. Estos cálculos determinan en gran medida la factibilidad de la construcción de embalses en regiones sujetas a altas tasas de evaporación. A diferencia de otras fases del ciclo hidrológico, la evaporación de cuerpos de agua no se puede medir directamente. Por lo tanto, a través de los años se han desarrollado varias metodologías alternativas para calcular la evaporación. Éstas están basadas en los siguientes procedimientos: (1) balance hídrico, (2) balance de energía, o (3) transferencia de masa. Método del balance hídrico para determinar la evaporación en un embalse. El método de balance hídrico asume que todas las fases pertinentes del ciclo hidrológico pueden ser evaluadas para un período de tiempo Δt dado, y expresadas en unidades de volumen. La evaporación de un embalse, reservorio, o lago se calcula con la siguiente formula: E = P  +  Q  -  O  -  I  -  ΔS (2-20) en la cual E = volumen evaporado, P = precipitación que cae directamente sobre el embalse, Q = escurrimiento superficial, o flujo de entrada al embalse, O = flujo de salida del embalse, I = volumen neto infiltrado en el suelo subyacente, y ΔS = cambio en el volumen almacenado en el embalse. Todos los términos de la Ec. 2-20 se refieren a un período de tiempo Δt, que usualmente se toma por lo menos de una semana. La mayoría de los términos de la Ec. 2-20 pueden ser evaluados directamente. La precipitación se mide fácilmente, y los flujos de entrada y salida se obtienen de los registros de escurrimiento. El cambio en el volumen almacenado se determina por medio del registro de los niveles de agua. La infiltración neta, sin embargo, sólo puede ser evaluada de manera indirecta, mediante la medición de la permeabilidad del suelo, o por la medición de cambios en el nivel de agua subterránea en pozos cercanos. La dificultad práctica de determinar la infiltración neta limita el método de balance hídrico a zonas con poca o ninguna infiltración neta. A pesar de esta limitación, el método del balance hídrico funciona en forma satisfactoria bajo ciertas condiciones ideales. Los estudios de balance hídrico del Lago Hefner, en Oklahoma, han demostrado que el método puede proporcionar volúmenes de evaporación dentro de una exactitud del 10%, aproximadamente dos terceras partes del tiempo [81]. Las condiciones en el Lago Hefner, sin embargo, eran muy selectivas, y es de esperar que para el caso típico la precisión del método sea menor. Método del balance de energía para determinar la evaporación en un embalse. Durante la evaporación, la superficie de agua está sujeta a intercambios significativos de energía. El cálculo de estos intercambios conduce al método de balance de energía para determinar la evaporación de un embalse. La cantidad de calor [energía] requerida para convertir un gramo de agua en vapor, es decir, el calor de vaporización, varía con la temperatura. Por ejemplo, a 20°C, el calor de vaporización es de 586 calorías (Tabla A-1, Apéndice A). Para mantener la temperatura de la superficie de evaporación, grandes cantidades de calor deben ser suministradas por radiación, por transferencia de calor de la atmósfera, y extraídas de la energía almacenada en el cuerpo de agua. La radiación es la emisión de energía, en forma de ondas electromagnéticas, que producen todos los cuerpos con temperatura superior a 0°K. 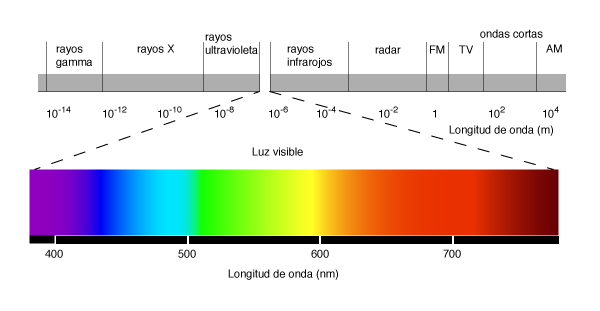La radiación solar recibida en la superficie de la Tierra constituye un componente importante del balance energético. La radiación solar alcanza el nivel exterior de la atmósfera a un flujo casi constante de cerca de 1.95 cal/cm2/min, o langleys/min (1 langley = 1 cal/cm2), medida perpendicularmente a la radiación incidente. Casi toda esta radiación es de longitudes de onda en el intervalo 0.3 a 3 μm, con aproximadamente la mitad de ella en el rango visible, 0.38 a 0.74 μm (Fig. 2-20). La Tierra también emite radiación, pero dado que su temperatura superficial es de cerca de 300°K, esta radiación es de mucho menor intensidad y mayor longitud de onda (3 a 50 μm) que la radiación solar. Dado que hay poco traslapo entre estos dos espectros de radiación, es común referir a la radiación solar como la radiación de onda corta, y a la radiación terrestre como radiación de onda larga [24]. Fig. 2-20  La luz visible en el espectro electromagnético. A su paso a través de la atmósfera, la radiación solar se separa en varias fracciones, cambiando su composición espectral. Parte de ella es reflejada y regresada al espacio; parte de ella es absorbida y dispersada por la atmósfera. A la fracción de radiación solar que llega directamente a la superficie de la Tierra se la denomina radiación solar directa. A la fracción de la radiación reflejada y dispersada por la atmósfera que eventualmente llega al terreno se la denomina radiación estelar. La radiación global es la suma de radiación solar directa y radiación estelar. 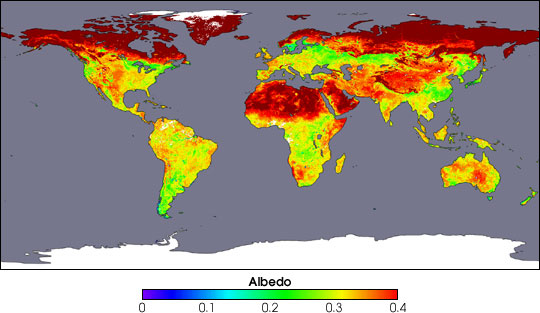El albedo es el coeficiente de reflectividad de una superficie dada con referencia a la radiación de onda corta. Este coeficiente varía con el color, rugosidad, e inclinación de la superficie. Su valor es de 0.03 a 0.1 para superficies de agua, de 0.05 a 0.3 para zonas con vegetación, de 0.15 a 0.4 para suelo descubierto, y hasta 0.95 para zonas cubiertas de nieve [24]. La Tabla 2-5 muestra los valores típicos de albedo. La Figura 2-21 muestra la distribución global de albedo. Tabla 2-5  Valores típicos de albedo. Bioma Albedo Lagos y océanos 0.03 - 0.10 Bosques 0.05 - 0.20 Pastizales 0.12 - 0.30 Tierras agrícolas 0.12 -0.25 Áreas urbanas 0.15 - 0.25 Suelo desnudo 0.15 - 0.40 Desiertos 0.20 - 0.45 Dunas 0.30 - 0.60 Nieve 0.50 - 0.95 Fig. 2-21  Distribución espacial global del albedo (NASA). 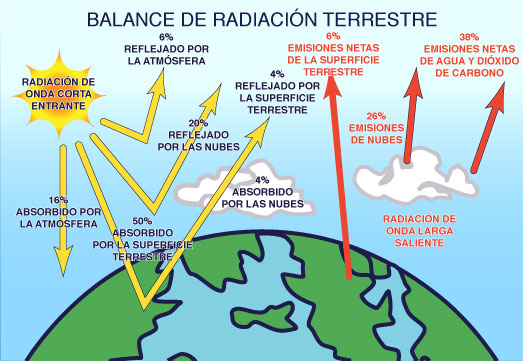Además del balance de radiación de onda corta, hay también el balance de radiación de onda larga. La superficie de la Tierra emite radiación, parte de la cual es absorbida y reflejada por la atmósfera. La diferencia entre los flujos salientes y entrantes se llama pérdida de radiación de onda larga. Durante el día, la radiación de onda larga puede ser una pequeña fracción de la radiación total, pero por la noche, en ausencia de la radiación solar, la radiación de onda larga domina el balance de radiación. La radiación neta, o efectiva, es igual a la radiación de onda corta neta (solar) menos la perdida de radiación de onda larga (terrestre) (Fig. 2-22). Fig. 2-22  Balance de radiación de la Tierra (NASA). En el método de balance de energía, la energía entrante se puede expresar con la ecuación siguiente: Qi  =  Qs ( 1 - A )  -  Qb  +  Qa (2-21) en la cual Qi = energía entrante; Qs = radiación global (radiación de onda corta, solar y celestial); A = albedo; Qb = pérdida de radiación de onda larga por el cuerpo de agua; y Qa = energía neta advectada (es decir, transmitida) a la masa de agua por arroyos, lluvia y nieve. El consumo de energía, el cual debe ser igual a la energía entrante, se expresa como sigue: Qo  =  Qh  +  Qe  +  Qt (2-22) en la cual Qo = energía saliente; Qh = transferencia de calor sensible desde el cuerpo de agua a la atmósfera, por convección y conducción; Qe = energía utlizada en el proceso de evaporación; y Qt = aumento de la energía almacenada en el cuerpo de agua. El valor de Qe es negativo para el caso de condensación. Todos los términos en las Ecs. 2-21 y 2-22 están dados en calorías por centímetro cuadrado por día. La energía utilizada en la evaporación Qe (cal/cm2/día) puede ser expresada como velocidad de evaporación equivalente E (cm/día) utilizando la siguiente fórmula: Qe = ρ λ E (2-23) en la cual ρ; = densidad del agua, en gramos por centímetro cúbico (g/cm3); λ = calor latente de vaporización, el cual es función de la temperatura (véase el cuadro A-1, Apéndice A), en calorías por gramo (cal / g); y E = velocidad de evaporación, en centímetros por día. Los términos Qh y Qe en la Ec. 2-22 son difíciles de evaluar mediante mediciones. Bowen ha sugerido que su relación es más manejable y que puede ser evaluada por la siguiente fórmula:            Qh              Ts - Ta           p B =  _______ = γ ___________  _________            Qe              es - ea         1000 (2-24) en la cual B = relación de Bowen, γ = parámetro psicrométrico, el cual es función de las propiedades físicas de aire seco, variando ligeramente con la temperatura (ver Tabla 2-6); Ts = temperatura del agua (cerca de la superficie), en grados Celsius; Ta = temperatura del aire (inmediatamente encima del agua), en grados Celsius; es = presión de vapor de saturación a la temperatura del agua, en milibares; ea = presión de vapor del aire, en milibares; y p = presión atmosférica, en milibares. Un balance de la energía entrante (Ec. 2-21) y saliente (Ec. 2-22), teniendo en cuenta las Ecs. 2-23 y 2-24, conduce a lo siguiente:            Qs ( 1 - A )  -  Qb  +  Qa  -  Qt E =  __________________________________                         ρ λ ( 1  +  B ) (2-25) Las cantidades Qs (1 - A) y Qb se pueden medir con radiómetros. La cantidad Qa se puede determinar mediante la medición de volúmenes y temperaturas del agua que fluye hacia dentro y fuera del cuerpo del agua, y Qt se evalúa mediante mediciones periódicas de la temperatura del agua. Un ejemplo de la aplicación del método de balance de energía para un gran lago es el estudio de la evaporación en el lago Ontario realizado por Bruce y Rodgers [9]. Método de la transferencia de masa. Las tasas de evaporación dependen de la temperatura de agua y de la presión atmosférica que prevalece localmente. Las temperaturas de agua más altas inducen una acción molecular más vigorosa, resultando en tasas de evaporación mayores. Por otro lado, la presión atmosférica más alta limita el movimiento de moléculas de agua y resulta en tasas de evaporación más bajas. En la práctica, el efecto de la presión atmosférica en la evaporación es pequeño y es usualmente despreciable. La presión en la interfase aire-agua, resultante del movimiento molecular en la dirección de escape del líquido, se llama presión de vapor de agua. Esta presión, la cual varía con la temperatura del agua como se muestra en la Tabla A-1 y la Tabla A-2 (Apéndice A), determina la velocidad a la que las moléculas de agua se escapan al aire y se convierten en moléculas de vapor de agua. Una vez en el aire, las moléculas de vapor de agua desplazan moléculas de aire y contribuyen su parte a la presión atmosférica total. Esta parte o fracción se denomina presión parcial de vapor. Cuando en un volumen de aire encima de un cuerpo de agua, la presión parcial de vapor está en equilibrio con la presión de vapor de agua, no hay intercambio neto de moléculas de agua; en consecuencia, se dice que el volumen de aire está saturado. Un volumen de aire saturado contiene todo el vapor de agua que puede contener. La presión de vapor de un volumen de aire saturado se denomina presión de vapor de saturación. Esta presión varía con la temperatura del aire y es idéntica a la presión de vapor de agua a esa temperatura. A mayor temperatura, mayor es la cantidad de vapor de agua que un volumen de aire puede contener, y mayor es la presión de vapor de saturación. La presión parcial de vapor (del aire) ea se calcula multiplicando la presión de vapor de saturación a la temperatura del aire (eo) por la humedad relativa, en porcentaje, y dividiendo por 100. Los estudios han demostrado que las tasas de evaporación son función de la diferencia entre la presión de vapor de saturación (a la temperatura de la superficie del agua o, como alternativa, a la temperatura del aire suprayacente) y la presión de vapor parcial del aire. 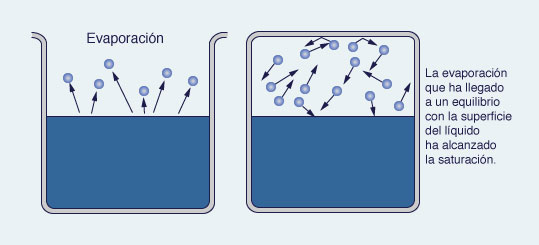A medida que continúa el proceso de evaporación, la capa más baja de la atmósfera alcanza eventualmente la saturación y, por consiguiente, la velocidad de evaporación neta disminuye a cero y puede hasta revertirse (condensación) (Fig. 2-23). Por lo tanto, un agente tal como el viento, el que abre el sistema y se lleva las moléculas de agua que salen de la superficie del agua, es necesario para que la evaporación continúe. Fig. 2-23  Modelo de la presión de vapor de saturación. El reconocimiento de estos procesos llevó a Dalton [15] a formular la clásica fórmula que lleva su nombre: E = f (u) ( es  -  ea ) (2-26) en la cual E = velocidad o tasa de evaporación; f(u) = una función de la velocidad del viento, en dirección horizontal; es = presión de vapor de saturación a la temperatura de la superficie del agua; y ea = presión parcial de vapor del aire suprayacente. Cuando el aire está saturado, es decir, cuando la humedad relativa se acerca al 100%, ea es casi igual a es, y la evaporación E tiende a cero. A través de los años, se han desarrollado varias ecuaciones empíricas del tipo de la Ec. 2-26. En conjunto, a éstas se la refiere como ecuaciones de transferencia de masa. Una ecuación de transferencia de masa comúnmente utilizada es la de Meyer [54]: E = C ( eo  -  ea ) [ 1 + ( W / 10 ) ] (2-27a) en la cual E = tasa de evaporación, en pulgadas por mes; C = un coeficiente que varía de 15 en pequeños estanques hasta 11 para lagos y embalses; eo = presión de vapor de saturación a la temperatura media mensual del aire, en pulgadas de mercurio; ea = presión de vapor del aire a la temperatura media mensual del aire, en pulgadas de mercurio; y W = velocidad del viento, media mensual, a la altura de 25 pies, en millas por hora. Otra versión de la ecuación de Meyer es la siguiente [55, 82]: E = C ( es  -  ea ) [ 1 + ( W / 10 ) ] (2-27b) en la que E = tasa de evaporación, en pulgadas por día; C = un coeficiente que varía de 0.50 para pequeños estanques hasta 0.36 para lagos y embalses; es = presión de vapor de saturación a la temperatura media diaria de la superficie del agua, en pulgadas de mercurio; ea = presión de vapor del aire a la temperatura media diaria del aire, en pulgadas de mercurio; y W = velocidad del viento, media diaria, a la altura de 25 pies, en millas por hora. Las siguientes ecuaciones de transferencia de masa han sido desarrolladas en relación con los estudios de evaporación del Lago Hefner [81]: E = 0.00304 ( es  -  e2 ) v4 (2-28a) E = 0.00241 ( es  -  e8 ) v8 (2-28b) en la cual E = tasa de evaporación, en pulgadas por día; es = presión de vapor de saturación de la superficie del agua, a la temperatura media diaria, en pulgadas de mercurio; e2 y e8 = presiones parciales de vapor (aire) sobre el lago, a 2 y 8 m de altura, respectivamente, en pulgadas de mercurio; y v4 y v8 = velocidades del viento sobre el lago, a 4 y 8 m de altura, respectivamente, en millas por día. Si e2 y v4 se toman contra el viento del lago, la constante en la Ec. 2-28a se reduce a 0.0027. Estas fórmulas han sido desarrolladas con los datos del balance hídrico del Lago Hefner, el cual tiene una superficie de 1,012 ha. Las fórmulas han sido probadas en el Lago Mead y otros embalses ubicados en el oeste de los Estados Unidos [10]. Métodos de combinación para determinar evaporación en un embalse. El uso conjunto de los métodos de balance de energía y transferencia de masa conduce a una forma alternativa para determinar la evaporación de un embalse. Penman [64] combinó estos dos conceptos en una fórmula de uso práctico. Un balance de energía aproximada (despreciando variaciones de energía en el cuerpo de agua, Qa = 0, y Qt = 0, en las Ecs. 2-21 y 2-22) condujo a Penman a la siguiente relación: Qs ( 1 - A )  -  Qb  =  Qh  +  Qe (2-29) El lado izquierdo de esta ecuación es la radiación neta, o Qn. El lado derecho se puede expresar en términos de la relación de Bowen (Ec. 2-24) como Qe (1 + B). Por lo tanto: Qn  =  Qe ( 1 + B ) (2-30) Mediante el uso de la Ec. 2-23, la Ec. 2-30 es expresada en unidades de evaporación (centímetros por día): En  =  E ( 1 + B ) (2-31) en la cual En = tasa de evaporación debida a radiación neta, y E = tasa de evaporación. Para p = 1,000 milibars, lo cual está muy cerca del valor de la presión atmosférica al nivel del mar (1013.2 milibars), la relación de Bowen (Ec. 2-24) se reduce a:               Ts  -  Ta            B =  γ   __________               es  -  ea          (2-32) El gradiente Δ de la presión de vapor de saturación con la temperatura, entre la superficie del agua y el aire suprayacente, en milibares por grado Celsius, se define como sigue:            es  -  eo            Δ =   ___________            Ts  -  Ta          (2-33) en el cual es = presión de vapor de saturación a la temperatura de la superficie del agua Ts, y eo = presión de vapor de saturación a la temperatura del aire Ta. La fórmula de Dalton (Ec. 2-26) permite el cálculo de la relación Ea /E, es decir, la relación de la tasa de evaporación debida a transferencia de masa Ea (suponiendo que las temperaturas de superficie del agua y del aire son iguales) a la tasa de evaporación E:    Ea            eo  -  ea            ______  =   ___________    E              es  -  ea          (2-34) Combinando las Ecs. 2-31 a 2-34, se obtiene la ecuación de Penman:             Δ En  +  γ Ea            E =   __________________                   Δ  +  γ          (2-35) en la cual E (tasa de evaporación total, o combinada), En (tasa de evaporación debida a la radiación neta) y Ea (tasa de evaporación debido a la transferencia de masa) se expresan en centímetros por día; y Δ y γ se expresan en milibares por grado Celsius. En la Ec. 2-35, las cantidades Δ y γ son factores de ponderación, afectando a las tasas por radiación neta y transferencia de masa, respectivamente. El gradiente Δ es función de la presión de vapor de saturación y la temperatura del aire (Ec. 2-33). Una fórmula simple basada únicamente en la temperatura del aire es [53]: Δ  =  ( 0.00815 Ta  +  0.8912 )7 (2-36) en la cual Δ se expresa en milibares por grado Celsius, y la temperatura Ta del aire está dada en grados Celsius. Esta fórmula es aplicable para temperaturas del aire superiores a -25 °C. El parámetro psicrométrico γ es directamente proporcional a la presión atmosférica e inversamente proporcional al calor latente de vaporización &lambda. Al nivel medio del mar, es decir, a la presión atmosférica estándar, γ varía ligeramente con la temperatura, como se muestra en la Tabla 2-6. La Ecuación 2-35 también se puede expresar como sigue:             α En  +  Ea            E =   ________________                  α  +  1          (2-37) en la cual α = Δ/γ es función de la temperatura del aire. Los valores de α (con Δ basado en la Ec. 2-36) se muestran en la Tabla 2-6. Tabla 2-6  Valores de γ y α en función de la temperatura del aire. Ta (oC) γ (mb / oC )1 α 0 0.655 0.683 5 0.658 0.928 10 0.661 1.246 15 0.664 1.654 20 0.668 2.166 25 0.671 2.812 30 0.674 3.616 35 0.677 4.607 40 0.681 5.813 1 A la presión atmosférica estándar (nivel medio del mar). La tasa de evaporación basada en transferencia de masa Ea se evalúa con una ecuación de transferencia de masa. Por ejemplo, Dunne [17] ha propuesto la siguiente fórmula:                                                      100 - φ            Ea =  ( 0.013 + 0.00016 v2 ) eo   __________                                                         100 (2-38) en el cual Ea = tasa de evaporación basada en transferencia de masa, en centímetros por día; v2 = velocidad del viento, medida a la profundidad de 2 m, en kilómetros por día; eo = presión de vapor de saturación a la temperatura del aire suprayacente, en milibares; y φ = humedad relativa, en porcentaje. Otras ecuaciones de tipo Penman se han desarrollado en los últimos 50 años. Por ejemplo, el Servicio Meteorológico Nacional ha desarrollado una ecuación de tipo Penman para la estimación de evaporación, basada en la temperatura media diaria del aire y el punto de rocío, el movimiento del aire por día, y la radiación solar [49, 51]. Los ejemplos más recientes de las ecuaciones de tipo Penman están representados por las fórmulas de Penman-Monteith [56] y Shuttleworth-Wallace [74] (véase la siguiente sección: Evapotranspiración). Ejemplo 2-4. Calcular la tasa de evaporación para al mes de enero, usando el método de Penman, dadas las siguientes condiciones atmosféricas: presión atmosférica estándar; temperatura del aire Ta = 20°C; radiación neta Qn = 550 cal/cm2/d; velocidad del viento (a 2 m por encima de la superficie) v2 = 200 km/d; y humedad relativa φ = 70%. La presión de vapor de saturación a la temperatura de 20°C (Tabla A-1, Apéndice A), es: eo = 23.37 milibares. La tasa de evaporación basada en transferencia de masa se calcula con la Ec. 2-38: Ea = 0.316 cm/d. El calor latente de vaporización a 20°C es (Tabla A-1): λ = 586 cal/g. La Ecuación 2-23 se utiliza para convertir la radiación neta a unidades de evaporación: En = (550 cal/cm2/d) / (0.998 g/cm3 × 586 cal/g) = 0.94 cm/d. La razón de Penman para Ta = 20°C se obtiene de la Tabla 6.2: α = 2.166. La tasa de evaporación diaria se calcula usando la Ec. 2-37: E = 0.743 cm/d. La evaporación correspondiente al mes de enero es de: 0.743 cm/d × 31 d = 23 cm.   CÁLCULO EN LÍNEA. Usando ENLINEA PENMAN, la solución es: ETo diario = 0.743 cm/d; ETo correspodiente al mes de enero = 23 cm. Determinación de la evaporación mediante el uso de tanques. La incertidumbre en la aplicabilidad de las diversas fórmulas ha llevado a la medición indirecta de la evaporación por medio de tanques. Un tanque de evaporación o evaporímetro es un instrumento diseñado para medir la pérdida de agua (en el tanque) durante un período de tiempo determinado, usualmente 1 día. El tanque proporciona una medición del efecto combinado de la radiación neta, viento, temperatura y humedad en la evaporación de una superficie de agua abierta a la atmósfera. Los tanques de evaporación varían considerablemente en tamaño, forma, materiales, y exposición a la atmósfera. En la práctica, es muy probable que la medición obtenida por el tanque sea algo mayor del valor actual de evaporación del lago adyacente (el prototipo). La relación de la evaporación del tanque a la del lago adyacente es una constante empírica; al recíproco de este valor se lo refiere como el coeficiente del tanque. La medición de evaporación utilizando tanques evaporímetros se trata en el Capítulo 3. 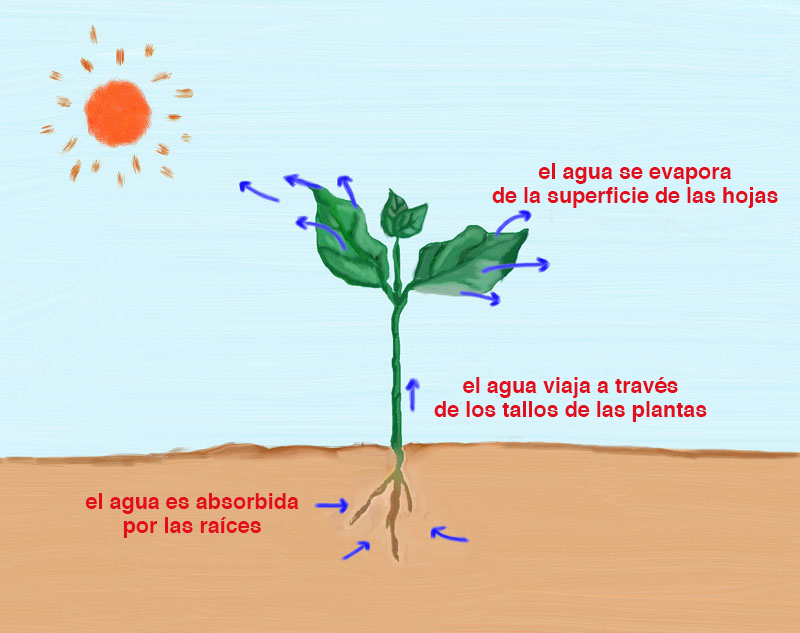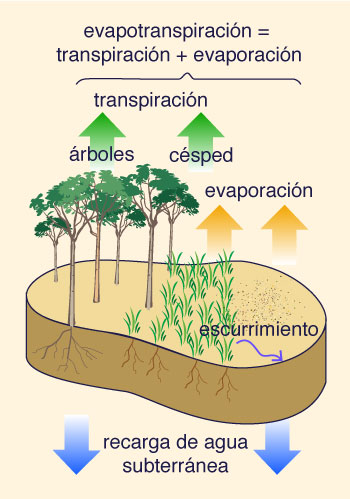Evapotranspiración La evapotranspiración es el proceso por medio del cual el agua de la superficie de la Tierra es convertida al estado de vapor y regresada a la atmósfera. Consiste de la evaporación de los cuerpos de agua, suelo, vegetación, y otras superficies, e incluye la transpiración de la vegetación. En este sentido, la evapotranspiración comprende toda el agua convertida en vapor y devuelta a la atmósfera y, por lo tanto, es un componente importante del balance hídrico de una cuenca a largo plazo. Fig. 2-24  Evapotranspiración. La transpiración es el proceso por medio del cual las plantas transfieren el agua de la zona radicular a la superficie de la hoja, donde eventualmente es evaporada. El proceso mediante el cual tiene lugar la transpiración se describe a continuación. 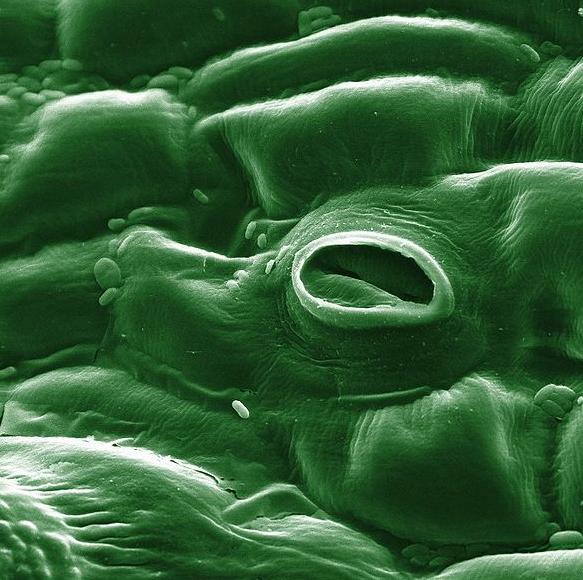La presión osmótica en la zona radicular actúa para mover el agua del suelo hacia las raíces. Una vez dentro de la raíz, el agua es transportada a través del tallo de la planta a los espacios intercelulares ubicados dentro de las hojas. El aire del ambiente circundante entra en las hojas a través de muy pequeñas aberturas superficiales llamadas estomas (Fig. 2-25). Los cloroplastos dentro de las hojas utilizan el dióxido de carbono del aire y una pequeña porción del agua disponible para la producción de los hidratos de carbono necesarios para el crecimiento de la planta. Al entrar el aire en la hoja, el agua escapa simultáneamente a través de los estomas, alcanzando la superficie, donde se hace disponible para evaporación. La proporción de agua transpirada y eventualmente evaporada a la que realmente se utiliza en el crecimiento de la planta es muy grande, de hasta 800 : 1 y aún mayor [53]. Fig. 2-25  Estoma de una hoja de tomate visto a través de un microscopio electrónico. La transpiración es una parte de la vida de la planta y, por lo tanto, es un proceso continuo, que se lleva a cabo con o sin la presencia de precipitación. Sin embargo, durante una tormenta, la intercepción puede utilizar parte de la energía disponible para evaporación, reduciendo así la cantidad de transpiración. La magnitud de este efecto varía con el tipo de vegetación. La transpiración está limitada por la velocidad a la cual la humedad se hace disponible para su uso por las plantas. Algunas autoridades opinan que la transpiración es independiente de la humedad del suelo, siempre y cuando ésta sea superior al punto de marchitamiento permanente, es decir, la humedad del suelo por debajo de la cual se produce el marchitamiento permanente. Sin embargo, otros investigadores asumen que la transpiración es aproximadamente proporcional a la humedad del suelo prevaleciente. Las tasas y cantidades de transpiración varían en forma considerable, dependiendo del tipo de vegetación, profundidad de la zona radicular, y extensión y densidad de la cubierta vegetal (Fig. 2-26). Las mediciones de transpiración son difíciles y suelen ser posible sólo bajo condiciones muy controladas. Dado que la transpiración resulta en evaporación, la cantidad de transpiración es función de los mismos factores meteorológicos y climáticos que controlan la tasa de evaporación. En la práctica, la transpiración se combina con la evaporación y se expresa como evapotranspiración, la cual incluye toda el agua que es convertida a vapor y devuelta a la atmósfera. Fig. 2-26  El proceso de transpiración. En los estudios de evapotranspiración se utiliza el concepto de evapotranspiración potencial, el cual se atribuye a Thornthwaite [78]. La evapotranspiración potencial es la cantidad de evapotranspiración que tendría lugar asumiendo en todo momento una amplia oferta de humedad (sin límite). Por lo tanto, la evapotranspiración potencial es un buen indicador del requerimiento óptimo de agua de un cultivo. En contraste con la evapotranspiración potencial, la evapotranspiración actual es la cantidad que tendría lugar en el caso de que la oferta de agua fuera limitada. Doorenbos y Pruitt [16] han desarrollado el concepto de evapotranspiración del cultivo de referencia ETo, el cual es similar al de evapotranspiración potencial. La evapotranspiración del cultivo de referencia es la tasa de evapotranspiración correspondiente a una superficie amplia, cubierta con una hierba de 8 a 15 cm de altura, de tamaño uniforme, en crecimiento activo, sombreando completamente el suelo, y sin escasez de agua. Por lo tanto, la evapotranspiración del cultivo de referencia se puede tomar como la evapotranspiración potencial del cultivo de referencia (un pasto corto verde). La evapotranspiración potencial es equivalente a la evaporación que se produciría en una superficie de agua lo suficientemente grande, pero con despreciable capacidad de almacenamiento de calor [50]. Por lo tanto, los métodos utilizados para calcular la evapotranspiración potencial son similares a los métodos utilizados para calcular la evaporación. Al igual que la evaporación, hay varios métodos para calcular la evapotranspiración potencial, cada uno con su propio rango de aplicabilidad. Los requerimientos de datos varían, lo que refleja los supuestos utilizados en el desarrollo de cada método. La mayoría de las fórmulas de evapotranspiración potencial son empíricas, relacionando aquélla con una o más variables meteorológicas o climáticas, tales como radiación, temperatura, velocidad del viento, y diferencia de presión de vapor. Otras fórmulas relacionan la evapotranspiración con mediciones directas de pérdidas de agua utilizando tanques de evaporación. Los modelos de evapotranspiración y evapotranspiración potencial se pueden agrupar en los siguientes grupos: Modelos de temperatura, Modelos de radiación, Modelos de combinación, y Modelos de tanque de evaporación. Cabe notar que, cuando se aplican a unas condiciones determinadas, las diversas fórmulas de evapotranspiración potencial generalmente dan resultados diferentes. Éstos, sin embargo, no varían mucho, con la relación de las estimaciones máximas y mínimas fluctuantes a través del año, y los cuales rara vez exceden la razón 2 : 1. Al igual que con cualquier cálculo, se requiere experiencia regional o local para elegir un método adecuado para calcular evapotranspiración potencial. Modelos de temperatura para calcular la evapotranspiración. La fórmula de Blaney-Criddle [5, 6] es típica de los modelos de temperatura para calcular la evapotranspiración. La fórmula ha sido ampliamente utilizada para estimar los requerimientos de agua de los cultivos. Su versión original, aplicable sobre una base mensual, tiene la siguiente forma: F  =  P T (2-39) en la cual F = evapotranspiración mensual, en pulgadas (por mes); P = variable relacionada con la duración diaria de luz, definida como la relación del total de horas de luz solar para el mes en referencia entre el total de horas de luz solar para todo el año, variable que es función de la latitud prevaleciente; y T = temperatura media del mes en referencia, en grados Fahrenheit. En unidades SI, aplicable sobre una base diaria, la fórmula de Blaney-Criddle es la siguiente: f  =  p ( 0.46 t + 8.13 ) (2-40) en la cual f = factor de uso consuntivo diario, en milímetros (por día); p = relación del promedio diario de horas de luz solar (durante el mes dado) entre el número total de horas de luz solar en el año, en porcentaje, el cual es función de la latitud prevaleciente (Tabla A-3, Apéndice A); y t = temperatura media diaria (para el mes dado), en grados Celsius. Para un cultivo determinado, el requerimiento de agua de consumo es la cantidad de agua necesaria para satisfacer las necesidades de evapotranspiración, sin que el crecimiento del cultivo esté limitado por falta de agua. El requerimiento de agua de consumo es igual al producto del factor f por un coeficiente empírico de uso consuntivo del cultivo en referencia kc. El requerimiento de agua de consumo varía ampliamente entre los climas con temperaturas similares y duraciones diarias de luz solar. Por lo tanto, el efecto del clima sobre el requerimiento de agua no está completamente descrito por el factor de uso consuntivo f. El efecto del clima puede ser incorporado en el coeficiente de cultivo kc. En general, el valor de kc depende del lugar y época del año. Usualmente es necesario realizar experimentos de campo locales con el fin de determinar su valor apropiado. Doorenbos y Pruitt [16] han propuesto una corrección a la fórmula de Blaney-Criddle para tomar en cuenta las siguientes condiciones climáticas locales: El tiempo relativo de insolación, es decir, la relación entre el número actual de horas de luz solar n y el valor máximo posible (N); La humedad relativa mínima (HR en la Fig. 2-27), en porcentaje; y La velocidad del viento diurno, medida a la altura de 2 m, en m/s. La ecuación de Doorenbos y Pruitt, comúnmente conocida como la fórmula FAO/Blaney-Criddle, es la siguiente: ETo  =  a  +  b f (2-41) en el cual ETo = evapotranspiración del cultivo de referencia, y a y b son el intercepto (medido desde el origen de coordenadas) y la pendiente, respectivamente, como se muestra en la Fig. 2-27, para tres niveles de tiempo relativo de insolación (bajo, medio y alto), humedad relativa mínima (baja, media y alta), y velocidad diurna del viento (ligera, moderada y fuerte). Fig. 2-27  Modificación de la fórmula de Blaney-Criddle según Doorenbos y Pruitt [16]. Usando la Fig. 2-27 como base, Frevert et al. [20] han desarrollado las siguientes ecuaciones de regresión para a y b : a  =  0.0043 φmin  -  n/N  -  1.41 (2-41a) b  =  0.81917  -  0.0040922 φmin  +  1.0705 n/N  +  0.065649 Ud         -  0.0059684 φmin (n/N) - 0.0005967 φmin Ud (2-41b) Para un cultivo dado, el requerimiento de agua de consumo ETc puede calcularse de la siguiente manera: ETc  =  kc ETo (2-42) La Tabla 2-7 muestra un rango aproximado de coeficientes estacionales de cultivos seleccionados. Tabla 2-7 (a) Coeficientes estacionales de cultivos. Cultivo kc Alfalfa 0.90 - 1.05 Aguacate 0.65 - 0.75 Plátanos 0.90 - 1.05 Frijoles 0.20 - 0.25 Cacao 0.95 - 1.10 Café 0.95 - 1.10 Algodón 0.50 - 0.65 Dátiles 0.85 - 1.10 Árboles caducifolios 0.60 - 0.70 Linaza 0.55 - 0.70 Granos (pequeños) 0.25 - 0.30 Toronja 0.70 - 0.85 Maíz 0.30 - 0.45 Semillas de aceite 0.25 - 0.40    Tabla 2-7 (b) Coeficientes estacionales de cultivos. Cultivo kc Cebolla 0.25 - 0.40 Naranja 0.60 - 0.75 Papa 0.25 - 0.40 Arroz 0.45 - 0.65 Sorgo 0.30 - 0.45 Soya 0.30 - 0.45 Remolacha 0.50 - 0.65 Caña de azúcar 1.05 - 1.20 Camotes 0.30 - 0.45 Tabaco 0.30 - 0.45 Tomate 0.30 - 0.45 Vegetales 0.15 - 0.30 Viñedos 0.30 - 0.55 Nueces 0.65 - 0.75 Ejemplo 2-6. Calcular la evapotranspiración del cultivo de referencia usando el método de Blaney-Criddle, para el mes de marzo y una ubicación de 35°N, con temperatura media diaria de 18°C. Asumir tiempo relativo de insolación: medio; humedad relativa mínima: media; y velocidad del viento diurno: moderada. Según la Tabla A-3 (Apéndice A): p = 0.27. Utilizando la Ec. 2-40: f = 4.43 mm/d. De la Fig. 2- 27, para f = 4.43 mm/d, y el tiempo relativo de insolación medio, humedad relativa mínima media y velocidad del viento diurno moderada (gráfico V, curva 2), ETo = 4.0 mm/día. Para el mes de marzo: ETo = 4.0 mm/día × 31 días = 124 mm.   CÁLCULO EN LÍNEA. Usando EN LÍNEA BLANEY-CRIDDLE, la respuesta es: ETo diario = 3.96 mm/d; ETo mensual (Marzo) = 122.9 mm. El método de Thornthwaite es otro modelo de temperatura ampliamente utilizado para estimar la evapotranspiración potencial [78]. El método se basa en un índice de eficiencia de temperatura anual J, definido como la suma de doce (12) valores mensuales del índice de calor I. Cada índice I es una función de la temperatura media mensual T, en grados Celsius, como sigue:              T               I  =  ( _____ ) 1.514              5               (2-43) La evapotranspiración se calcula por la siguiente fórmula:                              10 T               PET (0) =  1.6  ( ______ ) c                                J               (2-44) en el cual PET(0) = evapotranspiración potencial correspondiente a la latitud 0°, en centímetros por mes; y c es un exponente dado por la siguiente fórmula: c = 0.000000675 J 3  -  0.0000771 J 2  +  0.01792 J  +  0.49239 (2-45) Para latitudes diferentes a 0°, la evapotranspiración potencial se evalúa de la siguiente manera: PET  =  K PET (0) (2-46) en la cual K es una constante para cada mes del año, que varía en función de la latitud (véase el cuadro A-4, Apéndice A). Ejemplo 2-7. Calcular la evapotranspiración potencial utilizando la fórmula de Thornthwaite durante el mes de julio para una ubicación geográfica a 30°N, con la siguientes temperaturas medias mensuales, en grados Celsius (enero a diciembre): 6, 8, 10, 12, 14, 18, 22, 20, 16, 12, 10, 8. El índice de eficiencia de temperatura J es la suma de los 12 valores de índice de calor mensual I (Ec. 2-43). Por lo tanto, J = 53.738. De la Ec. 2-45: c = 1.337. De la Ec. 2-44: PET(0) = 10.54 cm (julio). Consultando la Tabla A-4 del Apéndice A, K = 1.16. Utilizando la Ec. 2-46, PET = 12.226 cm (julio).   CÁLCULO EN LÍNEA. Usando ENLINEA THORNTHWAITE, la evapotranspiración potencial para el mes de julio es: ETo = 12.227 cm. Modelos de radiación. Priestley y Taylor [67] han propuesto que la evapotranspiración potencial se tome como la componente de radiación de la ecuación de Penman (Ec. 2-35, asumiendo Ea = 0) afectada con una constante empírica. La fórmula Priestley y Taylor es la siguiente:                 1.26 Δ [ Qn / (ρ H ) ]            PET =   ________________________                           Δ  +  γ          (2-47a) en la cual PET = evapotranspiración potencial, en centímetros por día; Qn = radiación neta, en calorías por centímetro cuadrado por día; Δ = gradiente definido por las Ecs. 2-33 y 2-36; y γ es el parámetro psicrométrico (Tabla 2-6). La Ecuación 2-47a ecuación también puede ser expresada como sigue:                 1.26 α [ Qn / (ρ λ ) ]            PET =   ________________________                           α  +  1          (2-47b) en la cual la constante α se puede obtener de la Tabla 2-6. Una evaluación más reciente de la fórmula de Priestley-Taylor ha confirmado su aplicabilidad a climas húmedos. Sin embargo, para una mejor estimación en climas áridos, la constante empírica debe ser tomada como 1.74 en lugar de 1.26 [75]. Ejemplo 2-8. Usando la fórmula Priestley-Taylor, calcular la evapotranspiración potencial correspondiente al mes de abril para un clima árido. Asumir Ta = 20°C y Qn = 600 cal/cm2/d. Para la temperatura dada, la densidad y el calor latente de vaporización (del agua) son: ρ = 0.998 g/cm3, y λ = 586 cal/g, respectivamente (Tabla A-1, Apéndice A). Por lo tanto, la radiación neta en unidades de evaporación (usando la Ec. 2-23) es: En = 600/(0.998 × 586) = 1.026 cm/d. De la Tabla 2.6: α = 2.166. Utilizando la Ec. 2.47, pero afectada con el coeficiente 1.74 (clima árido), la evapotranspiración potencial diaria es: PET = 1.221 cm/d. La evapotranspiración potencial mensual es: PET (abril) = 1.221 × 30 = 36.63 cm.   CÁLCULO EN LÍNEA. Usando PRIESTLEY-TAYLOR EN LÍNEA: ETo diario = 1.221 cm/d; ETo  para el mes de abril = 36.63 cm. Modelos de tanque de evaporación. Los tanques de evaporación proporcionan una medida del efecto integrado de la radiación, viento, temperatura, y humedad en la evaporación de una superficie de agua abierta a la atmosfera. Cabe anotar que las plantas y vegetación responden a las mismas condiciones climáticas, pero varios factores producen diferencias apreciables en la pérdida de agua por evaporación. El albedo de una superficie de agua está en el rango 0.03 - 0.10, mientras que en la mayoría de las superficies vegetativas este rango es de 0.12 - 0.30 (Tabla 2-5). El almacenamiento de calor en el tanque durante el día puede ser considerable, y puede causar casi igual evaporación entre la noche y el día, mientras que la mayoría de los cultivos experimentan un 95% de evaporación durante las horas de luz solar. Además, la ubicación del tanque y el medio ambiente local influyen en la evaporación medida por el tanque, particularmente cuando el tanque está ubicado en sitios con vegetación y no en sitios de barbecho. A pesar de estas limitaciones, con una ubicación y mantenimiento adecuados, además del uso de equipamiento estándar, los tanques de evaporación continúan usándose para la estimación de los requerimientos de agua de los cultivos. La fórmula básica para evaporación potencial usando un tanque es la siguiente: PET  =  Kp Ep (2-48) en la cual PET = evapotranspiración potencial; Kp = coeficiente del tanque; y Ep = evaporación medida por el tanque. Los tanques de evaporación más comunes son el tanque NWS Clase A y el tanque hundido de Colorado. El tanque NWS Clase A es circular, de 122 cm de diámetro y 25.4 cm de profundidad, construído de hierro galvanizado (calibre 22) o metal Monel® (0.8 mm) (Fig. 2-28). El tanque está montado sobre una plataforma de madera con su base a 15 cm por encima del suelo, y nivelado. Se llena con agua hasta 5 cm por debajo del borde, y el nivel de agua se mantiene dentro de 7.5 cm por debajo del borde. Fig. 2-28  El tanque de evaporación Clase A (benmeadows.com). El tanque hundido de Colorado es a veces preferible debido a que tiende a producir una mejor estimación de la evapotranspiración del cultivo de referencia que el tanque Clase A. La sección transversal del tanque es un cuadrado de 920 mm de lado y 460 mm de profundidad. Está construído de hierro galvanizado y se coloca en el terreno con su borde superior a 50 mm por encima de aquél. (Fig. 2-29). La superficie de agua en el tanque se mantiene al nivel del terreno, o ligeramente por debajo de éste. Fig. 2-29  El tanque hundido de Colorado. El tanque de evaporación es ampliamente utilizado en la estimación de evapotranspiración potencial. Stanhill [76], por ejemplo, concluyó que el tanque Clase A es el método más apropiado para estimar la evapotranspiración potencial. Doorenbos y Pruitt [16] han elaborado recomendaciones para selecccionar un valor adecuado del coeficiente Kp del tanque, aplicable a condiciones climáticas y locales diversas (ver Tabla 2-8). Tabla 2-8  Coeficiente Kp aplicable para el tanque NWS Clase A [16].   Tanque rodeado de vegetación verde corta Tanque rodeado de terreno seco de barbecho Humedad relativa (%)   Baja 40 Media 40-70 Alta 70   Baja 40 Media 40-70 Alta 70 Velocidad del viento (km/d) Distancia (contra el viento) a la vegetación verde corta (m)   Distancia (contra el viento) al terreno seco de barbecho (m)   Ligera (menos de 175) 0 0.55 0.65 0.75 0 0.70 0.80 0.85 10 0.65 0.75 0.85 10 0.60 0.70 0.80 100 0.70 0.80 0.85 100 0.55 0.65 0.75 1000 0.75 0.85 0.85 1000 0.50 0.60 0.70 Moderada (175-425) 0 0.50 0.60 0.65 0 0.65 0.75 0.80 10 0.60 0.70 0.75 10 0.55 0.65 0.70 100 0.65 0.75 0.80 100 0.50 0.60 0.65 1000 0.70 0.80 0.80 1000 0.45 0.55 0.60 Fuerte (425-700) 0 0.45 0.50 0.60 0 0.60 0.65 0.70 10 0.55 0.60 0.65 10 0.50 0.55 0.65 100 0.60 0.65 0.70 100 0.45 0.50 0.60 1000 0.65 0.70 0.75 1000 0.40 0.45 0.55 Muy fuerte (mayor de 700) 0 0.40 0.45 0.50 0 0.50 0.60 0.65 10 0.45 0.55 0.60 10 0.45 0.50 0.55 100 0.50 0.60 0.65 100 0.40 0.45 0.50 1000 0.55 0.60 0.65 1000 0.35 0.40 0.45 1 Para áreas extensas de suelo desnudo y sin desarrollo agrícola, los coeficientes del tanque se reducen los siguientes valores: (1) 20% bajo condiciones de viento caliente; y (2) 5-10% para condiciones moderadas de viento, temperatura y humedad. 2.3  CARACTERÍSTICAS DE LA CUENCA [Escurrimiento]   [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Precipitación]   [Abstracciones Hidrológicas]   El escurrimiento superficial ocurre en forma progresiva de las siguientes formas, de pequeña a grande: Flujo superficial de lámina, Flujo en canaletas, Flujo en cárcavas, Corrientes, y Ríos. El flujo superficial es el escurrimiento que se produce durante o inmediatamente después de una tormenta, usualmente en forma de flujo laminar sobre la superficie del terreno [Fig. 2-30 (a)]. El flujo en canaletas es el escurrimiento a través de muy pequeños canales, como resultado de la concentración lineal del flujo superficial. El flujo en cárcavas es el escurrimiento que se ha concentrado en profundidades lo suficientemente grandes como para tener el poder erosivo de tallar su propio canal, usualmente profundo y estrecho (b). El flujo de corriente concentra el escurrimiento superficial en canales con profundidades bien definidas (c). Las corrientes llevan el flujo hacia corrientes cada vez más grandes, para eventualmente desembocar en los ríos (d). Fig. 2-30 (a)  Flujo superficial. Fig. 2-30 (b)  Flujo en cárcava. Fig. 2-30 (c)  Flujo de corriente. Fig. 2-30 (d)  Flujo de río. El tamaño de una cuenca puede variar desde menos de 1 ha (o acre) hasta millones de kilómetros cuadrados (o millas cuadradas). [La cuenca del río Amazonas, la más grande del mundo, tiene una extensión de 6,915 millones de km2]. En las cuencas pequeñas, el escurrimiento es controlado principalmente por el flujo superficial de lámina; por otro lado, en las cuencas grandes, el escurrimiento es controlado por la cantidad de almacenamiento de volumen en los cauces fluviales. Entre las cuencas pequeñas y las grandes, existe una gran variedad de tamaños de cuencas con características de escurrimiento intermedias. Independientemente de su tamaño, las cuencas pueden drenar ya sea hacia el interior, a los lagos (o, en regiones áridas, a lagos estacionalmente secos), o hacia el exterior, en dirección al océano. Las cuencas que drenan hacia el interior tienen drenajes endorreicos, e decir, continentales interiores (Fig. 2-31). Las cuencas que drenan hacia el exterior tienen drenajes exorreicos, es decir, continentales exteriores, o periféricos. Los drenajes exorreicos tienen su boca en su punto más bajo, en el lugar de entrega a la corriente localizada aguas abajo, usualmente de mayor tamaño, y en última instancia, al océano. Fig. 2-31   La Gran Cuenca, la mayor cuenca endorreica de los Estados Unidos de América. Las características hidrológicas de una cuenca se describen en términos de las siguientes propiedades: (1) área, (2) forma, (3) desniveles en la altitud, (4) medidas lineales, (5) topología, (6) densidad de cauces, y (7) patrones de drenaje. El área de la cuenca El área de la cuenca, o área de drenaje, es tal vez la propiedad más importante. Aquélla determina el volumen potencial de escurrimiento, particularmente en el caso de que la tormenta cubra toda el área. La divisoria de la cuenca, o divortium aquarium, es el lugar geométrico de los puntos que delimitan dos cuencas vecinas, es decir, la colección de los puntos topográficamente altos (la secuencia de picos de montañas y sillas intermedias) que separan dos cuencas vecinas. Debido al posible efecto del flujo subsuperficial (el flujo de agua subterránea), la divisoria hidrológica puede no coincidir exactamente con la divisoria topográfica (Fig. 2-32). Sin embargo, la divisoria hidrológica es más difícil de determinar que la divisoria topográfica; por lo tanto, esta última es preferida para propósitos prácticos. Fig. 2-32  Un río que aflora directamente de la tierra, cerca de Huánuco, Perú. La divisoria de la cuenca se delinea en un mapa topográfico adecuado. La dirección del escurrimiento superficial es perpendicular a las líneas de contorno. El procedimiento consiste en identificar primeramente todos los picos y las sillas (Fig. 2-33). El escurrimiento de un pico es en todas las direcciones; el escurrimiento de una silla es en las dos direcciones opuestas, perpendiculares al eje de la silla. La divisoria de la cuenca se obtiene uniendo picos y sillas con una línea mantenida perpendicular a las líneas de contorno. El área encerrada por la divisoria topográfica es medida con el fin de determinar el área de captación o de drenaje. Fig. 2-33  Delimitación de la divisoria de cuenca del Arroyo Campo, en el Condado de San Diego, California (los picos y sillas se muestran como puntos de color púrpura). En general, cuanto mayor sea el área de drenaje, mayor será la cantidad de escurrimiento superficial. Se han propuesto varias fórmulas para relacionar la descarga máxima (o descarga pico) con el área de drenaje (Capítulo 7). La siguiente es una fórmula básica: Qp  =  c A n (2-49) en el cual Qp = descarga máxima, o descarga pico, A = área de captación, o de drenaje, y c y n = parámetros a determinarse mediante un análisis de regresión. Otros métodos para calcular la descarga máxima están basados en la descarga máxima por unidad de área, por ejemplo, el método TR-55 (Capítulo 5). La forma de una cuenca La forma de una cuenca es la forma descrita por la proyección de la superficie de una cuenca sobre un plano horizontal. Horton [28] describió el contorno usual de una cuenca como un ovoide en forma de pera. Las grandes cuencas, sin embargo, varían mucho en forma. La siguiente relación provée una descripción cuantitativa [26]:               A Kf  =  _______              L 2 (2-50) en el cual Kf = razón de forma, A = área de la cuenca, y L = longitud de la cuenca, medida a lo largo del curso de agua predominante (el más largo). El área y la longitud se dan en unidades consistentes, por ejemplo, kilómetros cuadrados y kilómetros, respectivamente. An alternate description is based on catchment perimeter rather than area. For this purpose, an equivalent circle is defined as a circle of area equal to that of the catchment. The compactness ratio is the ratio of the catchment perimeter to that of the equivalent circle. This leads to: Una descripción alternativa está basada en el perímetro de la cuenca. Para este propósito, se define un círculo equivalente de área igual a la de la cuenca. La razón de compacidad es la relación entre el perímetro de la cuenca y el perimetro del círculo equivalente. Esto lleva a:              0.282 P Kc  =  ____________                 A 1/2 (2-51) en el cual Kc = razón de compacidad, P = perímetro de la cuenca, y A = área de la cuenca, con P y A expresados en cualquier conjunto consistente de unidades. La respuesta hidrológica se refiere a la concentración y tiempo de ocurrencia del escurrimiento (Fig. 2-34). El rol de la forma de la cuenca en la respuesta hidrológica no ha sido establecido con certeza. En igualdad de condiciones, una razón de forma elevada (Ec. 2-50) o una razón de compactación cercana a 1 (Ec. 2-51) describe una cuenca con una respuesta hidrológica rápida y con picos. Por el contrario, una razón de forma baja o una razón compacidad mucho mayor que 1 describe una cuenca con una respuesta hidrológica lenta. Sin embargo, muchos otros factores, incluidos las diferencias de elevación, la cubierta vegetal, y la densidad de drenaje suelen ser más importantes que la forma de la cuenca, y su efecto combinado no es usualmente discernible. Fig. 2-34  Respuesta hidrológica de la cuenca del río La Leche, Lambayeque, Perú. El relieve de una cuenca El relieve de una cuenca es la diferencia de elevación entre dos puntos de referencia establecidos. El relieve máximo de una cuenca es la diferencia de cota entre el punto más alto de la divisoria de cuenca (por ejemplo, la Fig. 2-35) y la boca de la cuenca. El curso principal (o corriente principal) es el mayor o más grande curso de agua de la cuenca, el cual transporta el escurrimiento superficial hacia la boca. La relación de relieve es la relación entre el relieve máximo y la distancia horizontal más larga, medida en la dirección del curso principal. La relación de relieve es una medida de la intensidad de los procesos erosivos en la cuenca. Fig. 2-35   El punto más alto en la cuenca del río Missouri, en la frontera entre los estados de Montana y Idaho, EE.UU. (Haga clic -aquí- para desplegar). La curva hipsométrica se usa para describir el relieve general de una cuenca [52]. Ésta es una curva adimensional que muestra la variación, con la elevación, de la subzona de captación localizada por encima de la elevación (Fig. 2-36). Para desarrollar esta curva, se identifica la elevación del punto más alto de la cuenca, que corresponde al cero por ciento de área; además, se identifica la elevación del punto más bajo, que corresponde al cien por ciento del área. Posteriormente, se seleccionan varias elevaciones, situadas entre máxima y mínima, y se determinan las subáreas superiores subtendidas por cada una de estas elevaciones. Las elevaciones se convierten a altura sobre la elevación mínima y se expresan en porcentaje de la altura máxima. Del mismo modo, las subáreas superiores subtendidas se expresan en porcentaje del área total de la cuenca. La curva muestra hipsométrica muestra el área relativa en el abscisas y la altura relativa en las ordenadas (Fig. 2-36). La elevación media de la cuenca se obtiene de la altura relativa correspondiente al cincuenta por ciento del área relativa. Fig. 2-36  Ejemplo de una curva hipsométrica. La curva hipsométrica se utiliza cuando una variable hidrológica, como la precipitación, la cubierta vegetal, o la cobertura de nieve muestra una marcada tendencia a variar con la altitud. En tales casos, la curva hipsométrica proporciona los medios cuantitativos para evaluar el efecto de la altitud. Otras medidas del relieve de una cuenca se basan en las características de las corrientes naturales. El perfil longitudinal es un gráfico de elevación versus distancia horizontal (Fig. 2-37). En un punto dado en el perfil, la elevación es generalmente un valor medio del fondo del canal. Entre dos puntos dados, el gradiente del canal (o pendiente del canal) es la relación entre la diferencia de elevación y la distancia horizontal que los separa. Fig. 2-37  Forma típica del perfil longitudinal de las corrientes naturales. En ausencia de controles geológicos, los perfiles longitudinales de los arroyos y ríos son generalmente cóncavos hacia arriba, es decir, muestran una disminución persistente en el gradiente del fondo en la dirección aguas abajo, conforme el flujo se mueve desde los arroyos de montaña hacia los valles, para terminar en el océano (Fig. 2-37). La razón para esta disminución aguas abajo en el gradiente requiere de un análisis cuidadoso. Se conoce que los gradientes de fondo están directamente relacionados con la fricción e inversamente relacionados con la profundidad de flujo. Por lo general, los pequeños arroyos de montaña tienen valores altos de fricción de fondo (debido a la presencia de guijarros y cantos rodados en el lecho) y profundidades pequeñas [[Fig. 2-38 (a)]. Por el contrario, los grandes ríos tienen valores relativamente bajos de fricción de fondo y profundidades grandes [Fig. 2-38 (b)]. Esta interacción de gradiente del canal y la fricción de fondo ayuda a explicar la disminución típica de gradiente en la dirección aguas abajo. Fig. 2-38 (a)  Arroyo Rachichuela, Lambayeque, Perú. Fig. 2-38 (b)  Desembocadura del río Amazonas, Amapá, Brasil. Los perfiles de fondo convexos (Fig. 2-39) son causados por tectonismo, controles geológicos o afloramientos rocosos que predominan sobre la morfología usual de tipo aluvial. Estos perfiles convexos generalmente conducen a la deposición de sedimentos aguas arriba del afloramiento y a erosión inmediatamente aguas abajo. Fig. 2-39   Perfil de fondo, Arroyo El Barbon-Guadalupe, Baja California, México. Las pendientes de las corrientes o ríos suelen expresarse en unidades adimensionales. Por conveniencia, pueden también ser expresadas en m km-1, cm km-1, o pies milla-1. En la naturaleza, las pendientes varían grandemente, desde mayores a 0,1 en arroyos de montaña muy empinados [véase, por ejemplo, la Fig. 2-38 (a)], a menos de 0,000006 en grandes ríos sujetos a efectos de marea [19]. En ciertas configuraciones geomorfológicas inusuales, algunos ríos interiores pueden presentar muy pequeños gradientes de canal; por ejemplo, el río Alto Paraguay, cerca de Porto Murtinho, Brasil, que tiene una inclinación de canal de 2 cm km-1 (S = 0,00002) (Fig. 2-40). Fig. 2-40  Río Alto Paraguay río cerca de Porto Murtinho, Brasil. La pendiente principal de un curso de agua es un indicador conveniente de las características topográficas. Un perfil longitudinal se define por dos puntos, el primero aguas arriba, de máxima elevación, y el segundo aguas abajo, de mínima elevación, y por la distancia horizontal entre ellos (Fig. 2-41). El gradiente obtenido directamente de estas elevaciones se conoce como la pendiente S1. Una medida un poco más representativa del gradiente es la pendiente S2, definida como la pendiente constante que hace que el área sombreada por encima de ella sea igual al área sombreada por debajo de ella (Fig. 2-41). La pendiente S2 se puede calcular igualando el área total por debajo de ella con el área total por debajo del perfil longitudinal. Fig. 2-41  Diagrama explicativo de las pendientes S1 y S2. La pendiente equivalente S3 es una medida de la pendiente que tiene en cuenta el tiempo de respuesta de la cuenca. Para calcular esta pendiente, la corriente o río se divide en n subtramos y se calcula una pendiente para cada subtramo. En base a la ecuación de Manning (Sección 2.4), se asume que el tiempo del viaje del flujo a través de cada subtramo es inversamente proporcional a la raíz cuadrada de la pendiente. De la misma manera, se asume que el tiempo del viaje a través de toda la corriente o río es inversamente proporcional a la raíz cuadrada de la pendiente equivalente. Esto conduce a la siguiente ecuación:                       n                      Σ Li                      i = 1 S3  =  [ _______________  ] 2                 n                Σ ( Li / Si 1/2 )                i = 1 (2-52) en el cual S3 = pendiente equivalente, Li = cada una de n longitudes de subtramo, y Si = cada una de n pendientes de subtramo. En las evaluaciones de escorrentía, a menudo se utilizan métodos de cuadrícula para obtener una medida de la pendiente de la superficie de la cuenca. Por ejemplo, el Servicio de Conservación de Recursos Naturales de los EE.UU. (NRCS) determina la pendiente media de la superficie mediante la superposición de una cuadrícula sobre el mapa topográfico de la cuenca [79]. Se evalúa la pendiente máxima en cada intersección, y se calcula y el promedio de todos los valores (Fig. 2-42). Este promedio se toma como el valor representativo de la pendiente de la superficie de la cuenca. Fig. 2-42  Superposición de una cuadrícula en nuna cuenca para determinar la pendiente de la superficie terrestre. Ejemplo 2-9. Dado un perfil longitudinal con las siguientes distancias y elevaciones, calcular las pendientes S1, S2 y S3. Distancia (m) 0 5,000 10,000 15,000 20,000 Elevación (m) 900 910 930 960 1000 Las elevaciones máximas y mínimas son 1000 y 900 m, respectivamente. La distancia horizontal entre ellas es de 20000 m. Por lo tanto, S1 = 100 / 20000 = 0,005. Con referencia a la Fig. 2-41, S2 = Y / 20000. El área bajo el perfil longitudinal es 750 000 m2. El área bajo S2 es: 20000 Y / 2 = 10000 Y. Por lo tanto, Y = 75 m, y S2 = 75 / 20000 = 0,00375. Los tramos individuales son de 5000 m de longitud, y las pendientes individuales son 0,002, 0,004, 0,006 y 0,008, respectivamente. La aplicación de la Ec. 2-52 conduce a S3 = 0,0041. Los resultados se muestran en la Fig. 2-43. Fig. 2-43  Las pendientes S1, S2, y S3. Medidas lineales Las medidas lineales se utilizan para describir las características unidimensionales de una cuenca. Por ejemplo, para las pequeñas cuencas, la longitud de flujo superficial o longitud de flujo en cuenca Lo es la distancia de escurrimiento superficial que trancurre antes de llegar a un canal unidimensional claramente definido. La longitud de cuenca o longitud hidráulica L es la longitud medida a lo largo del curso principal de una cuenca (Fig. 2-44). El curso principal (o corriente principal) es el curso de agua más grande de la cuenca, el cual transporta el flujo a la boca de la cuenca. Fig. 2-44  Medidas lineales de una cuenca. La longitud al centroide de la cuenca Lc es la longitud medida a lo largo del curso principal hasta un punto situado más cerca del centro de gravedad de la cuenca (el punto G de la Fig. 2-44). En la práctica, el centro de gravedad se estima como el punto de intersección de dos o más líneas rectas que bisectan la cuenca en subáreas aproximadamente iguales. Topología de una cuenca La topología de una cuenca se refiere o define la anatomía regional de la red hidrográfica. La modelación distribuida de lluvia-escorrentía (Capítulo 10) requiere la descripción jerárquica de la conectividad de la corriente, es decir, de su topología. Orden de una corriente. El concepto de orden de una corriente clasifica los flujos de una red hidrográfica siguiendo un sistema jerárquico de numeración. El flujo en cuenca puede ser considerado como una corriente hipotética de orden cero. Una corriente de primer orden recibe el flujo de una o más corrientes de orden cero, es decir, las colecciones de flujo superficial. Dos corrientes de primer orden se combinan para formar una corriente de segundo orden. En general, dos corrientes de orden m se combinan para formar una corriente de orden m + 1. El orden de una cuenca es el orden del subtramo principal que deposita el flujo en la boca de la cuenca (Fig. 2-45). Fig. 2-45  E; concepto de orden de una corriente. El orden de una cuenca está directamente relacionado con su tamaño. Las grandes cuencas pueden tener órdenes de 10 o más. La evaluación del orden depende mucho de la escala del mapa utilizado. Por lo tanto, es necesario tener mucho cuidado al utilizar un análisis de orden en estudios comparativos del comportamiento hidrológico de cuencas. El sistema de codificación de Pfasfstetter. El sistema Pfafstetter es una metodología ampliamente utilizada para la descripción de la topología de cuencas. El sistema describe la anatomía regional de una red hidrográfica de drenaje utilizando una codificación jerarquizada de dígitos decimales. El sistema Pfafstetter es importante porque asiste en la identificación de subcuencas (de varios niveles) procesadas con sistemas de información geográfica (SIG). Una cuenca de Nivel 0 corresponde a un tamaño de escala continental, es decir, una cuenca que drena hacia el océano. Los niveles (números) de codificación más altos representan subdivisiones progresivamente más pequeñas de la cuenca de Nivel 0. Teóricamente, el sistema no está limitado en el número de niveles. En la práctica, sin embargo, los niveles entre n = 6 a n = 8 son usualmente suficientes. En cada nivel, a cada cuenca se le asigna un número entero específico m, que varía de m = 0 a m = 9, dependiendo de su ubicación y función en la red de drenaje. En cada nivel, las cuencas hidrográficas se clasifican en tres tipos: (1) cuenca, (2) entrecuenca y (3) cuenca interna, como se muestra en la Tabla 2-9. Una cuenca es aquélla que no tiene flujo concentrado de entrada aguas arriba, pero sí de salida aguas abajo. Una entrecuenca es aquélla que tiene ambos flujo concentrados, de entrada aguas arriba y de salida aguas abajo. Una cuenca interna es aquélla que no tiene ni flujo concentrado de entrada ni de salida, es decir, es una cuenca endorreica o cerrada. Tabla 2-9  Subdivision de cuencas usando el sistema Pfafstetter. No. Tipo Flujo concentrado de entrada aguas arriba Flujo concentrado de salida aguas abajo 1 Cuenca NO SÍ 2 Entrecuenca SÍ SÍ 3 Cuenca interna NO NO Para cada nivel, de 1 a n, la asignación de los códigos de Pfafstetter se realiza de la siguiente manera: Desde la boca o salida de la cuenca, se rastrea hacia aguas arriba a lo largo del cauce principal, procediendo a identificar los cuatro (4) afluentes que tengan las mayores áreas de drenaje. Las subcuencas que contienen estos cuatro (4) afluentes se clasifican como cuencas, asignándoseles dígitos pares (m = 2, 4, 6 y 8), aumentando en dirección hacia aguas arriba. Las subcuencas intermedias (a las subcuencas pares), es decir, las que contribuyen entradas laterales al cauce principal, se clasifican como entrecuencas, asignándoseles dígitos impares (m = 1, 3, 5 y 7), aumentando en dirección hacia aguas arriba. El último dígito impar (m = 9) se reserva para la subcuenca de cabecera, es decir, aquélla que es tributaria a la entrecuenca 7. A la cuenca interna más grande, si existe, se le asigna el dígito m = 0. Si existieran otras cuencas internas, éstas son incorporadas a las cuencas, o entrecuencas, inmediatamente cercanas. En el caso inusual en el cual dos cuencas, por ejemplo, 2 y 4, drenen en el mismo lugar, en un lado o en lados opuestos, la entrecuenca intermedia (3) es considerada de área nula. La Figura 2-46 muestra un ejemplo de tres (3) niveles del sistema de codificación Pfasfstetter. Para cada nivel, por ejemplo el Nivel 3, los dígitos asignados (XYm) se conjuntan con el código del Nivel 2 (XY). Por ejemplo, la cuenca 846 es la cuenca 8 del Nivel 1 (más grueso), la cuenca 4 del Nivel 2 (intermedio) y la cuenca 6 del Nivel 3 (más fino). 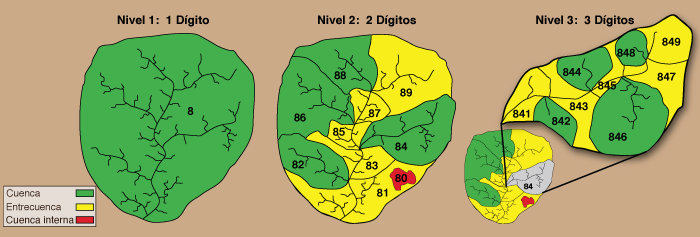Fig. 2-46  El sistema de codificación de Pfafstetter para la identificación de cuencas hidrográficas (Haga click -aquí- para desplegar). Densidad de Drenaje La densidad de drenaje de una cuenca es la relación de la longitud total de flujo superficial unidimensional (es decir, la suma de las longitudes de todas las corrientes) al area de la cuenca. Una alta densidad de drenaje refleja una respuesta rápida del flujo en la cuenca, mientras que una baja densidad de drenaje refleja una respuesta retardada. La longitud media del flujo superficial es aproximadamente igual a la mitad de la distancia media entre dos corrientes. Por lo tanto, se puede aproximar como la mitad del recíproco de la densidad de drenaje:                1 Lo  =  _______              2D (2-53) en el cual Lo = longitud media del flujo superficial, y D = densidad de drenaje. Esta aproximación no tiene en cuenta el efecto de las pendientes del terreno y corrientes, lo que hace que la longitud real media del flujo superficial sea mayor que la estimada por la Ecuación 2-53. La siguiente ecuación se puede usar para estimar la longitud media del flujo superficial en forma más precisa:                             1 Lo  =  _________________________              2D [ 1  -  (Sc /Ss) ] 1/2 (2-54) en la cual Sc = pendiente media de la corriente, y Ss = pendiente media del terreno. Patrones de drenaje Los patrones de drenaje que prevalecen en cuencas varían ampliamente; los más complejos son indicación de una alta densidad de drenaje. Los patrones de drenaje reflejan los efectos de la geología local, el suelo, y la vegetación (Fig. 2-47) y, a menudo están relacionados con propiedades hidrológicas como la respuesta de escorrentía o el rendimiento anual. La Figura 2-48 muestra varios tipos de patrones de drenaje reconocibles mediante el uso de fotografías aéreas [30]. Fig. 2-47  Efecto de la geología local en los patrones de drenaje. Fig. 2-48  Patrones de drenaje reconocibles en fotografías aéreas. 2.4  ESCURRIMIENTO [Preguntas]   [Problemas]   [Bibliografía]   •   [Arriba]   [Precipitación]   [Abstracciones Hidrológicas]   [Características de la Cuenca]   El término escorrentía superficial, o simplemente escorrentía, se refiere a todas las aguas que fluyen sobre la superficie de la Tierra, ya sea en forma de flujo laminar, o por flujo de canal abierto, en arroyuelos, barrancos, arroyos o ríos. La escorrentía superficial es un proceso contínuo por el cual el agua fluye constantemente de mayores a menores elevaciones, por acción de fuerzas gravitacionales. Los pequeños arroyos se combinan para formar arroyos más grandes que eventualmente crecen, para formar los ríos. Con el tiempo y espacio, los ríos llevan su flujo hacia el océano, completando el ciclo hidrológico. La escorrentía se expresa ya sea en términos de volumen o caudal. Las unidades de volumen de escorrentía son metros cúbicos. El caudal, o descarga, es el volumen que pasa a través de un área o sección dada en una unidad de tiempo, expresado en metros cúbicos por segundo, o alternativamente, en pies cúbicos por segundo. El caudal suele variar en el tiempo; por lo tanto, su valor en cualquier momento es el caudal instantáneo o local. El caudal local puede expresarse durante un período de tiempo como el valor promedio para ese período. La descarga o caudal puede integrarse en un período de tiempo para obtener el volumen de escorrentía acumulada, de la siguiente manera: ∀  =  ∫ Q dt  =  Σ Q Δt (2-55) en la cual ∀ = escorrentía, Q = caudal, t = tiempo, and Δt = incremento de tiempo. En la ingeniería hidrológica, la escorrentía se expresa comúnmente en unidades de profundidad. Esto se logra dividiendo el volumen de escurrimiento por el área de drenaje para obtener una profundidad de escorrentía equivalente distribuída sobre toda la cuenca. En ciertas aplicaciones, la escorrentía se expresa alternativamente en términos de: (1) flujo máximo por unidad de área de drenaje, (2) flujo máximo por unidad de profundidad de escorrentía, o (3) flujo máximo por área de drenaje, por unidad de profundidad de escorrentía. En el primer caso, las unidades son metros cúbicos por segundo por kilómetro cuadrado; en el segundo caso, metros cúbicos por segundo por centímetro; y en el tercer caso, metros cúbicos por segundo, por kilómetro cuadrado, y por centímetro. Componentes del escurrimiento Runoff may consist of water from three sources: El escurrimiento puede originar en: Flujo superficial, Entreflujo, y Flujo de agua subterránea. El flujo superficial es el producto de la precipitación efectiva, es decir, la precipitación menos las abstracciones hidrológicas. Al flujo superficial también se le denomina escurrimiento directo. El escurrimiento directo tiene la capacidad de producir grandes concentraciones de flujo en un período de tiempo relativamente corto. Por lo tanto, el escurrimiento directo es en gran parte responsable de los flujos de inundación. El entreflujo es el flujo subsuperficial, es decir, el flujo que tiene lugar en la zona vadosa, es decir, en las capas de suelo no saturados situadas debajo de la superficie del terreno (Fig. 2-49). El entreflujo consiste en el movimiento lateral del agua y la humedad hacia elevaciones más bajas, e incluye algunas de las precipitaciones abstraídas por la infiltración. Es característicamente un proceso lento, pero al final una fracción de los volúmenes de entreflujo desembocan en arroyos y ríos. Típicamente, las cantidades de entreflujo son relativamente pequeñas comparadas con las cantidades de flujo superficial y de aguas subterráneas. Fig. 2-49  La zona no saturada. El flujo de agua subterránea tiene lugar por debajo de la capa freática en forma de flujo saturado, a través de depósitos aluviales y otras formaciones geológicas y acuíferos situados bajo el manto del suelo (Fig. 2-50) (Capítulo 11). El flujo de agua subterránea incluye la parte del volumen infiltrado que ha alcanzado el nivel freático por percolación vertical. Como el entreflujo, el flujo de agua subterránea dr caracteriza por ser un proceso lento. Al igual que la escorrentía superficial, el flujo de agua subterránea es un proceso continuo, con el agua en constante movimiento a elevaciones más bajas (o a zonas de menor potencial). La mayor parte del flujo de agua subterránea es finalmente cortada por arroyos y ríos, descargando hacia ellos. Una pequeña porción del flujo de agua subterránea, particularmente la que fluye a grandes profundidades, poco a poco se abre paso hacia el océano más cercano. El tiempo de permanencia media global de las aguas subterráneas es de 1400 años [**]. Fig. 2-50 Dirección general del flujo de agua subterránea (U.S. Geological Survey). Tipos de corriente y caudal base Las corrientes naturales, es decir, ríos o arroyos, se pueden clasificar en tres tipos: Perenes, Efímeras, e Intermitentes. Los arroyos perennes son los que tienen flujo en forma permanente. Durante el período seco (es decir, en ausencia de lluvia), el flujo de los arroyos perennes es el llamado caudal base, el cual consiste principalmente de flujo de agua subterránea interceptado por la corriente. Los arroyos que se alimentan de agua subterránea se denominan corrientes efluentes. Los arroyos perennes y efluentes son típicos de regiones con clima subhúmedo o húmedo [(Fig. 2-51 (a)]. Las corrientes efímeras son las que fluyen sólo en respuesta directa a la precipitación, es decir, inmediatamente después de una tormenta considerable. Las corrientes efímeras no interceptan el flujo de las aguas subterráneas y, por lo tanto, no tienen caudal base. De otro lado, las corrientes efímeras generalmente contribuyen a la recarga de agua subterránea por infiltración a través de sus lechos porosos. Los arroyos que alimentan al agua subterránea se denominan arroyos influentes. A las abstracciones producidas por arroyos influentes se las denominan pérdidas por transmisión en el canal. Las corrientes efímeras e influentes son típicas de regiones con clima árido o semiárido [(Fig. 2-51 (b)]. Los arroyos intermitentes son aquéllos que muestran características mixtas, comportándose como perennes en la estación húmeda y efímeros en la estación seca. Dependiendo de las condiciones locales, estas corrientes pueden alimentar el agua subterránea, o alimentarse de ella [(Fig. 2-51 (c) y (d)]. Fig. 2-51 (a)  Corriente perenne: Arroyo Indian, California. Fig. 2-51 (b)  Corriente efímera: Río Mojave, California. Fig. 2-51 (c)  Corriente intermitente: Arroyo Rosarito, Baja California, México. Fig. 2-51 (d)  Corriente intermitente: Río Gila, Arizona. Estimaciones del flujo de base son importantes en la hidrología; por ejemplo, en el cálculo del volumen de escorrentía total producido por una cuenca en un año, referido como la producción anual de agua. En la hidrología de inundaciones, el flujo de base se utiliza para separar la escorrentía superficial en: (a) directa, e (b) indirecta. La escorrentía indirecta es la escorrentía superficial que proviene del agua subterr´anea. El flujo de base o caudal base es una medida de la escorrentía indirecta. Escorrentía superficial y caudal base. En la práctica, la escorrentía superficial puede o no incluir el caudal base. El término "escorrentía superficial" se utiliza a menudo para referirse a la escorrentía directa, excluyendo el caudal base. Sin embargo, a nivel de cuenca, las estimaciones de la producción de agua suelen incluir tanto la escorrentía directa como el caudal base. La confusión es con frecuencia una fuente de error en el análisis hidrológico. Por ejemplo, el método del número de la curva NRCS (Capítulo 5) fue desarrollado originalmente para el cálculo de la escorrentía superficial directa, aplicable a cuencas pequeñas. Sin embargo, a lo largo de los años desde su creación, el método también se ha utilizado para el cálculo de la escorrentía superficial de cuencas más grandes, las cuales pueden incluir el caudal base. Humedad antecedente La precipitación efectiva es la fracción de la precipitación total que permanece en la superficie después que se han producido todas las abstracciones hidrológicas. Durante períodos lluviosos, la infiltración juega un papel importante en la abstracción de la precipitación. Las velocidades, y las cantidades de infiltración asociadas, varían ampliamente, siendo altamente dependientes de la humedad inicial del suelo. La humedad del suelo varía con la historia de precipitación antecedente, aumentando con la precipitación antecedente y disminuyendo con la falta de ésta. Para una tormenta dada, la historia de la precipitación previa al evento, que pudo haber causado la humedad del suelo a departir de un estado normal, se denomina "humedad antecedente". Una cuenca con baja humedad antecedente (por ejemplo, una cuenca más seca de lo normal) no es propicia para grandes cantidades de escorrentía directa. Por otro lado, una cuenca con alta humedad antecedente (por ejemplo, una cuenca más húmeda de lo normal) sí es propicia para grandes cantidades de escorrentía directa (Fig. 2-52). Fig. 2-52  Una cuenca con alta humedad antecedente: Arroyo Campo, California, el 5 de marzo de 2005, después de varios días de lluvia. El reconocimiento de que la escorrentía directa es una función de la humedad antecedente ha llevado al concepto de índice de precipitación antecedente (IPA). El nivel medio de humedad en una cuenca varía diariamente, aumentando con la precipitación y disminuyendo con la evaporación y evapotranspiración. La hipótesis de una tasa de agotamiento logarítmica conduce a la IPA de una cuenca para un día sin lluvia: Ii  =  K I i-1 (2-56) en la cual Ii = índice del día i, Ii-1 = índice del día i -1, y K = factor de recesión tomado normalmente en el rango 0,85 ≤ K ≤ 0,98 [53]. Si la lluvia se produce en cualquier día, se añade la altura de lluvia al índice. El índice en el día 0 (valor inicial) tendría que ser estimado. Del mismo modo, el valor aplicable de K se determina a partir ya sea de datos o experiencia. El IPA está directamente relacionado con la profundidad de escurrimiento. Cuanto mayor sea el valor del índice, mayor es la cantidad de escurrimiento. En la práctica, la regresión y otras herramientas estadísticas se utilizan para relacionar el escurrimiento con el IPA. Estas relaciones son invariablemente empíricas y por lo tanto estrictamente aplicables solamente a la situación para la cual se derivaron. Otras medidas de humedad de cuenca se han desarrollado a lo largo de los años. Por ejemplo, el Servicio de Conservación de Recursos Naturales (NRCS, por sus siglas en Inglés) utiliza el concepto de condición de humedad antecedente (AMC) (capítulo 5), que agrupa a la humedad de cuenca en tres niveles: AMC I, una condición seca; AMC II, una condición media; y AMC III, una condición húmeda. Condiciones de humedad que varían entre AMC II y AMC III se utilizan normalmente en el diseño hidrológico. Otro ejemplo del uso del concepto de humedad antecedente es el del modelo SSARR (Capítulo 13). Este modelo calcula el volumen de escurrimiento en función de una relación que vincula el porcentaje de escurrimiento con un índice de humedad del suelo (SMI), usando la intensidad de precipitación como tercera variable. El porcentaje de escurrimiento es la relación de escurrimiento a lluvia, multiplicada por 100. Dicha relación de escurrimiento-humedad-lluvia es empírica y, por lo tanto, se limita a la cuenca para la cual se ha derivado. Relaciones precipitación-escurrimiento La precipitación se puede medir de una manera relativamente simple, mediante el uso de un pluviómetro. Sin embargo, las mediciones de escurrimiento requieren por lo general de un procedimiento de aforo elaborado (Capítulo 3). Esta diferencia ha llevado a que los datos de precipitación sean más accesibles que los datos de escurrimiento. La cuenca típica tiene muchos más pluviómetros que estaciones de aforo, y los registros de precipitación son usualmente más largos que los registros de aforo. El hecho de que los datos de precipitación sean más fáciles de conseguir que los datos de escorrentía ha llevado al cálculo de la escorrentía en base a datos de precipitación. Aunque éste es un procedimiento indirecto, se ha demostrado su viabilidad en una variedad de aplicaciones. Un modelo linear básico de precipitación-escurrimiento está dado por la siguiente fórmula: Q  =  b ( P - Pa ) (2-57) en el cual Q = profundidad de escurrimiento, P = profundidad de precipitación, Pa = profundidad de precipitación por debajo de la cual el escurrimiento es nulo, y b = pendiente de la línea recta (Fig. 2-53). Las profundidades de precipitación menores que Pa están completamente abstraídas por la cuenca, y el escurrimiento comienza cuando P excede Pa. Para utilizar la Ec. 2-57 es necesario colectar varios conjuntos de datos de precipitación-escurrimiento y realizar una regresión linear para determinar los valores de b y Pa (Capítulo 7). La simplicidad de la Ec. 2-57 no permite que ésta tome en cuenta otros mecanismos productores de escurrimiento, como intensidad de precipitación, velocidad de infiltración, y/o humedad antecedente. En la práctica, la correlación muestra generalmente un amplio rango de variación, lo que limita su capacidad predictiva. Fig. 2-53  Un modelo linear básico de precipitación-escurrimiento. El efecto de la velocidad de infiltración y la humedad antecedente en el escurrimiento es ampliamente reconocido. Se han desarrollado varios modelos en un intento de simular estos y otros procesos. Un modelo típico es el del número de la curva NRCS, el cual ha tenido una gran aceptación en la práctica. El modelo NRCS se basa en una relación no lineal lluvia-escurrimiento, el cual incluye una tercera variable (el parámetro de la curva) denominado número de la curva, o CN. En una aplicación particular, el valor de CN está determinado por una evaluación detallada del tipo de suelo, patrones de vegetación y uso del suelo, humedad antecedente, y la condición hidrológica de la superficie. El método del número de la curva NRCS se describe en el capítulo 5. La concentración del escurrimiento La propiedad de concentración es una característica muy importante del escurrimiento superficial. Para describirla, supongamos que una tormenta dada produce una intensidad de precipitación efectiva distribuida uniformemente en toda la cuenca. En tal caso, el escurrimiento superficial (es decir, la descarga) se concentra finalmente a la salida de la cuenca, cuando la duración efectiva de la precipitación es suficientemente larga. La concentración del escurrimiento implica que la descarga a la salida de la cuenca aumenta desde cero, gradualmente, hasta que la precipitación en toda la cuenca haya tenido tiempo para viajar a la salida y contribuir al flujo en ese punto. En ese momento se alcanza el máximo caudal, que es a la vez el caudal de equilibrio, lo cual indica que el escurrimiento superficial se ha concentrado en la salida. Al tiempo que tarda un elemento de agua en viajar desde el punto más lejano hasta la boca de la cuenca se le denomina tiempo de concentración. El caudal de equilibrio es igual a la intensidad de la lluvia efectiva por el área de influencia: Qe  =  Ie A (2-58) en la cual Qe = caudal de equilibrio; Ie = intensidad de la lluvia efectiva; y A = área de drenaje. Esta ecuación es dimensionalmente consistente; sin embargo, es necesario el uso de un factor de conversión en el lado derecho para tener en cuenta las unidades usuales. Por ejemplo, en unidades SI, con Qe en litros por segundo, Ie en milímetros por hora, y A en hectáreas, el factor de conversión es de 2.78. En las unidades habituales de los Estados Unidos, con Qe en pies cúbicos por segundo, Ie en pulgadas por hora, y A en acres, el factor de conversión es 1,008, el cual a menudo se desestima. ------------------- 201208 10:45 ------------------- The process of runoff concentration can lead to three distinct types of catchment response. The first type occurs when the effective rainfall duration is equal to the time of concentration. In this case, the runoff concentrates at the outlet, reaching its maximum (equilibrium) rate after an elapsed time equal to the time of concentration. Rainfall stops at this time, and subsequent flows at the outlet are no longer concentrated because not all the catchment is contributing. Therefore, the flow gradually starts to recede back to zero. Since it takes the time of concentration for the farthest runoff parcels to travel to the outlet, the recession time is approximately equal to the time of concentration, as sketched in Fig. 2-54. (In practice, due to nonlinearities, actual recession flows are usually asymptotic to zero). This type of response is referred to as concentrated catchment flow. El proceso de concentración de la escorrentía puede dar lugar a tres tipos distintos de respuesta de captación. El primer tipo se produce cuando la duración efectiva la precipitación es igual al tiempo de concentración. En este caso, el escurrimiento se concentra en la salida, alcanzando su máximo (equilibrio) la tasa después de un tiempo transcurrido igual al tiempo de concentración. Las precipitaciones se detiene en este momento, y los flujos posteriores a la salida ya no se concentran, porque no toda la cuenca está contribuyendo. Por lo tanto, el flujo comienza gradualmente a retroceder de nuevo a cero. Dado que lleva el tiempo de concentración para las parcelas de escorrentía más lejanos para viajar a la salida, el tiempo de recesión es aproximadamente igual al tiempo de concentración, como esbozado en la Fig. 2-54. (En la práctica, debido a las no linealidades, los flujos de recesión reales son generalmente asintótica a cero). Este tipo de respuesta se denomina flujo de captación como concentrado. Fig. 2-54  Concentrated catchment flow. Flujo de captación concentrado. The second type of catchment response occurs when the effective rainfall duration exceeds the time of concentration. In this case, the runoff concentrates at the outlet, reaching its maximum (equilibrium) rate after an elapsed time equal to the time of concentration. Since rainfall continues to occur, the whole catchment continues to contribute to flow at the outlet, and subsequent flows remain concentrated and equal to the equilibrium value. After rainfall stops, the flow gradually recedes back to zero. Since it takes the time of concentration for the farthest runoff parcels to travel to the outlet, the recession time is approximately equal to the time of concentration, as shown in Fig. 2-55. This type of response is referred to as superconcentrated catchment flow. Did you mean: The second type of catchment response occurs when the effective rainfall duration exceeds the time of concentration. In this case, the runoff concentrates at the outlet, reaching its maximum (equilibrium) rate after an elapsed time equal to the time of concentration. Since rainfall continues to occur, the whole catchment continues to contribute to flow at the outlet, and subsequent flows remain concentrated and equal to the equilibrium value. After rainfall stops, the flow gradually recedes back to zero. Since it takes the time of concentration for the farthest runoff parcels to travel to the outlet, the recession time is approximately equal to the time of concentration, as shown in Fig. 2-55. This type of response is referred to as super concentrated catchment flow. El segundo tipo de respuesta de captación se produce cuando la duración efectiva de lluvia excede el tiempo de concentración. En este caso, el escurrimiento se concentra en la salida, alcanzando su máximo (equilibrio) la tasa después de un tiempo transcurrido igual al tiempo de concentración. Desde precipitaciones persiste, toda la cuenca sigue contribuyendo a fluir en la salida, y los flujos posteriores permanecer concentrada e igual al valor de equilibrio. Después de paradas de precipitación, el flujo se aleja poco a poco de nuevo a cero. Dado que lleva el tiempo de concentración para las parcelas de escorrentía más lejanos para viajar a la salida, el tiempo de recesión es aproximadamente igual al tiempo de concentración, como se muestra en la Fig. 2-55. Este tipo de respuesta se refiere al flujo de captación como superconcentrado. Fig. 2-55  Superconcentrated catchment flow. / Flujo de captación superconcentrado. The third type of response occurs when the effective rainfall duration is shorter than the time of concentration. In this case the flow at the outlet does not reach the equilibrium value. After rainfall stops, the flow recedes back to zero. The requirements that volume be conserved and recession time be equal to the time of concentration lead to the idealized flat top response shown in Fig. 2-56. This type of response is referred to as subconcentrated catchment flow. El tercer tipo de respuesta se produce cuando la duración efectiva la precipitación es más corto que el tiempo de concentración. En este caso el flujo en la salida no alcanza el valor de equilibrio. Después de la lluvia se detiene, el flujo retrocede de nuevo a cero. Los requisitos que debe ser conservado volumen y tiempo recesión ser igual al tiempo de concentración de plomo a la respuesta plana superior idealizada se muestra en la Fig. 2-56. Este tipo de respuesta se refiere al flujo de captación como subconcentrated. Fig. 2-56  Subconcentrated catchment flow. / Flujo de captación Subconcentrated. In practice, concentrated and superconcentrated flows are typical of small catchments, i.e., those likely to have short times of concentration. On the other hand, subconcentrated flows are typical of midsize and large catchments, i.e., those with longer times of concentration. Figure 2-57 shows actual dimensionless hydrographs depicting the three types of catchment flows. En la práctica, los flujos concentrados y superconcentradas son típicos de las pequeñas cuencas, es decir, aquellos propensos a tener tiempos cortos de concentración. Por otra parte, los flujos de subconcentrated son típicos de medianas y grandes zonas de captación, es decir, aquellos con tiempos más largos de concentración. La figura 2-57 muestra hidrogramas sin dimensiones reales que representan los tres tipos de flujos de captación. Fig. 2-57  Hidrogramas adimensionales que muestran tres tipos de flujo de captación. Time of Concentration. Hydrologic procedures for small catchments usually require an estimate of the time of concentration (Chapter 4). However, precise estimations are generally difficult. For one thing, time of concentration is a function of runoff rate; therefore, an estimate can only represent a certain flow level, whether it be low flow, average flow, or high flow. Tiempo de Concentración. Procedimientos hidrológicos de cuencas pequeñas por lo general requieren una estimación del tiempo de concentración (capítulo 4). Sin embargo, las estimaciones precisas son generalmente difíciles. Por un lado, el tiempo de concentración es una función de la velocidad de escurrimiento; por lo tanto, una estimación sólo puede representar un cierto nivel de flujo, ya sea de bajo flujo, caudal medio, o de alto flujo. Several formulas for the calculation of time of concentration are available. Most are empirical in nature and, therefore, of somewhat limited value. Nevertheless, a few are widely used in practice. An alternate approach is to calculate time of concentration by dividing the principal watercourse into several subreaches and assuming an appropriate flow level for each subreach. Subsequently, a steady open-channel flow formula such as the Manning equation is used to calculate the mean velocity and associated travel time through each subreach. The time of concentration for the entire reach is the sum of the times of concentration of the individual subreaches. This procedure, while practical, is based on several assumptions, including a flow-rate level, a prismatic channel, and Manning's n values. Varias fórmulas para el cálculo del tiempo de concentración están disponibles. La mayoría son empírica en la naturaleza y, por lo tanto, del valor algo limitado. Sin embargo, unos pocos son ampliamente utilizados en la práctica. Un enfoque alternativo consiste en calcular el tiempo de la concentración dividiendo el curso de agua director en varios subtramos y asumiendo un nivel de flujo adecuado para cada subtramo. Posteriormente, una fórmula de flujo de canal abierto constante tal como la ecuación de Manning se utiliza para calcular la velocidad media y el tiempo de viaje asociados a través de cada subtramo. El tiempo de concentración para todo el alcance es la suma de los tiempos de concentración de los subtramos individuales. Este procedimiento, mientras que práctico, se basa en varios supuestos, incluyendo un nivel de velocidad de flujo, un canal prismático, y n valores de Manning. A limitation of the steady flow approach to the calculation of time of concentration is the fact that the flow being considered is generally unsteady. This means that the speed of travel of the wavelike features of the flow (i.e., the kinematic wave speed, Chapters 4 and 9) is greater than the mean velocity calculated using steady flow principles (the Manning equation). For instance, for turbulent flow in hydraulically wide channels, kinematic wave theory justifies a wave speed as much as 5/3 times the mean flow velocity, with a consequent reduction in travel time and associated time of concentration. Yet, in many cases, the ratio between kinematic wave speed and mean flow velocity is likely to be less than 5/3:1. In practice, the uncertainties involved in the computation of time of concentration have contributed to a blurring of the distinction between the two speeds. Una limitación del enfoque de flujo constante para el cálculo del tiempo de concentración es el hecho de que el flujo está considerando es generalmente inestable. Esto significa que la velocidad de desplazamiento de las características en forma de onda del flujo (es decir, la velocidad de onda cinemática, los capítulos 4 y 9) es mayor que la velocidad media calculada utilizando los principios de flujo estacionario (la ecuación de Manning). Por ejemplo, para el flujo turbulento en canales hidráulicamente de ancho, la teoría de onda cinemática justifica una velocidad de onda tanto como 5/3 veces la velocidad media del flujo, con la consiguiente reducción del tiempo de viaje y el tiempo asociado de la concentración. Sin embargo, en muchos casos, la relación entre la velocidad de onda cinemática y la media de la velocidad del flujo es probable que sea menos de 5/3: 1. En la práctica, las incertidumbres involucradas en el cálculo del tiempo de concentración han contribuido a un desdibujamiento de la distinción entre las dos velocidades. Formulas for Time of Concentration. Notwithstanding the inherent complexities, calculations of time of concentration continue to be part of the routine practice of engineering hydrology. The time of concentration is a key element in the rational method (Chapter 4) and other methods used to calculate the runoff response of small catchments. Most formulas relate time of concentration to suitable length, slope, roughness, and rainfall parameters [62]. A well-known formula which relates time of concentration to length and slope parameters is the Kirpich formula, applicable to small agricultural watersheds with drainage areas less than 8 acres (200 ha) [46]. In SI units, the Kirpich formula is: Fórmulas para Tiempo de Concentración. A pesar de las complejidades inherentes, los cálculos de tiempo de concentración siguen siendo parte de la práctica habitual de la hidrología de la ingeniería. El tiempo de concentración es un elemento clave en el método racional (Capítulo 4) y otros métodos utilizados para calcular la respuesta escorrentía de pequeñas cuencas. La mayoría de las fórmulas relacionan tiempo de concentración de longitud adecuada, pendiente, rugosidad, y los parámetros de lluvia [62]. Una conocida fórmula que relaciona el tiempo de la concentración de parámetros de longitud y pendiente es la fórmula Kirpich, aplicable a pequeñas cuencas agrícolas con áreas de drenaje de menos de 8 acres (200 ha) [46]. En las unidades del SI, la fórmula Kirpich es:                              L 0.77 tc  =   0.06628  ___________                             S 0.385 (2-59) in which tc = time of concentration, in hours; L = length of the principal watercourse, from divide to outlet, in kilometers; and S = slope between maximum and minimum elevation (S1 slope), in meters per meter. In U.S. customary units, with tc in minutes, L in feet and S in feet per foot, the coefficient of Eq. 2-83 is 0.0078. en el que TC = tiempo de concentración, en horas; L = longitud del curso de agua principal de la división a la salida, en kilómetros; y S = pendiente entre la elevación máxima y mínima (pendiente S1), en metros por metro. En Estados Unidos las unidades habituales, con tc en minutos, L en pies y S en pies por pie, el coeficiente de la ecuación. 2-83 es 0.0078. The Kerby-Hathaway formula relates time of concentration to length, slope, and roughness parameters as follows [22]: La fórmula Kerby-Hathaway relaciona tiempo de concentración de longitud, pendiente y parámetros de rugosidad de la siguiente manera [22]:                         ( L n ) 0.467 tc  =   0.606  _______________                             S 0.234 (2-60) in which n is a roughness parameter and all other terms are the same as in Eq. 2-59, expressed in SI units. Applicable values of n are given in Tabla 2-10. en la que n es un parámetro de rugosidad y todos los demás términos son los mismos que en la ecuación. 2-59, expresada en unidades del SI. Valores aplicables de n se dan en la Tabla 2-10. Tabla 2-10  Value of roughness parameter n for use in Eqs. 2-60 to 2-63 [10]. / Valor del parámetro de rugosidad n para su uso en Ecuaciones. 2-60 a 2-63 [10]. Type of surface / Tipo de superficie n Smooth impervious / suave impermeable 0.02 Smooth bare-picked soil / Suelo desnudo recogido liso 0.10 Poor grass, row crops, or moderately rough bare soil / La mala hierba, cultivos en hileras o suelo desnudo moderadamente áspera 0.20 Pasture / Pastura 0.40 Deciduous timber land / Tierra de hoja caduca madera 0.60 Coniferous timber land, or deciduous timber land with deep litter or grass / La tierra de la madera de coníferas, o la tierra de madera de hoja caduca con cama profunda o la hierba 0.80 The Papadakis-Kazan formula [62] relates time of concentration to length, slope, roughness, and rainfall parameters: La fórmula Papadakis-Kazan [62] se relaciona tiempo de concentración a la longitud, pendiente, rugosidad, y los parámetros de precipitaciones:                       L 0.50  n 0.52 tc  =  0.66  _________________                      S 0.31  i 0.38 (2-61) in which tc is in minutes; L is in feet; n is a roughness parameter; and i is the effective rainfall in inches per hour. en el que tc es en minutos; L está en los pies; n es un parámetro de rugosidad; y i es la precipitación efectiva en pulgadas por hora. A physically based approach to the calculation of time of concentration is possible by means of overland flow techniques (Chapter 4). As a first approximation, time of concentration can be taken as the time-to-equilibrium of kinematic overland flow (Eq. 4-50). Therefore: Un enfoque basado físicamente para el cálculo del tiempo de concentración es posible por medio de técnicas de flujo terrestres (Capítulo 4). Como una primera aproximación, el tiempo de la concentración puede ser tomado como el equilibrio tiempo-a-de flujo superficial cinemática (Ec. 4-50). Por consiguiente:                      (L n) 1/m tc  =   ______________________               S 1/(2 m)  i (m - 1)/m (2-62) in which tc is given in seconds; L is in meters; n is a roughness parameter, i is in m/s, and m = exponent of the unit-width discharge-flow depth rating (q = b h m ). en el que se da tc en segundos; L es en metros; n es un parámetro de rugosidad, i es en m / s, y m = exponente de la aprobación de la gestión del flujo de calificación profundidad unidad de anchura (q = BHM). For m = 5/3, applicable to turbulent Manning friction (in hydraulically wide channels), the kinematic wave time of concentration is: Para m = 5/3, aplicable a turbulento fricción Manning (en los canales hidráulicamente de ancho), el tiempo de onda cinemática de concentración es:               (L n) 0.6 tc  =   ______________              S 0.3  i 0.4 (2-63) in which tc is in seconds; L is in meters; n is a roughness parameter; and i is the effective rainfall in meters per second. The close resemblance of the exponents of Eqs. 2-61 and 2-63 is remarkable. en el que tc es en cuestión de segundos; L es en metros; n es un parámetro de rugosidad; y i es la precipitación efectiva en metros por segundo. El parecido de los exponentes de las ecuaciones. 2-61 y 2-63 es notable. Example 2-10. / Ejemplo 2-10. Use the Kirpich, Hathaway, Papadakis-Kazan, and kinematic wave formulas to estimate time of concentration for a catchment with the following characteristics: L = 750 m, S = 0.01, n = 0.1, and i = 20 mm hr -1. Utilice la Kirpich, Hathaway, Papadakis-Kazan, y las fórmulas de ondas cinemáticas para estimar el tiempo de la concentración de una cuenca con las siguientes características: L = 750 m, S = 0,01, n = 0,1, y i = 20 mm hr -1. After conversion to the proper units, the application of Eq. 2-59 leads to tc = 0.3127 hr = 18.76 minutes. The application of Eq. 2-60 leads to tc = 0.531 hr = 31.86 minute. The application of Eq. 2-61 leads to tc = 45.13 minutes. The application of Eq. 2-62 leads to tc = 6716 seconds = 111.94 minutes. Después de la conversión a las unidades apropiadas, la aplicación de la ecuación. 2-59 conduce a Tc = 0,3127 h = 18.76 minutos. La aplicación de la ecuación. 2-60 conduce a Tc = 0.531 h = 31,86 minutos. La aplicación de la ecuación. 2-61 conduce a Tc = 45.13 minutos. La aplicación de la ecuación. 2-62 conduce a Tc = 6716 segundos = 111.94 minutos.   ONLINE CALCULATION. Using ONLINE TIME OF CONCENTRATION, the answer is: Kirpich ⇒ tc = 18.76 minutes; Kerby-Hathaway ⇒ tc = 31.73 minutes; Papadakis-Kazan ⇒ tc = 45.13 minutes. Kinematic wave ⇒ tc = 111.95 minutes. El cálculo online. Usando TIEMPO LÍNEA DE CONCENTRACIÓN, la respuesta es: Kirpich ̉ tc = 18,76 minutos; Kerby-Hathaway ̉ tc = 31.73 minutos; Papadakis-Kazan ̉ tc = 45.13 minutos. Onda cinemática ̉ tc = 111.95 minutos. Runoff Diffusion and Streamflow Hydrographs / Difusión escorrentía y Tránsito de hidrogramas In nature, catchment response shows a more complex behavior than that which may be attributed solely to runoff concentration. Theory and experimental evidence have shown that runoff rates are governed by natural processes of convection and diffusion. Convection refers to runoff concentration; diffusion is the mechanism acting to spread the flow rates in time and space. En la naturaleza, la respuesta de captación muestra un comportamiento más complejo que el que se puede atribuir únicamente a la concentración de la escorrentía. La teoría y la evidencia experimental han demostrado que las tasas de escorrentía se rigen por procesos naturales de convección y difusión. La convección se refiere a la concentración de la escorrentía; la difusión es el mecanismo que actúa para difundir las velocidades de flujo en tiempo y espacio. The net effect of runoff diffusion is to reduce the flow rates to levels below those that could be attained by convection only. In practice, diffusion acts to smooth out catchment response. The resulting response function is usually continuous, and it is referred to as the streamflow hydrograph, runoff hydrograph, or simply the hydrograph. Typical single-storm hydrographs have a shape similar to that shown in Fig. 2-58. They are usually produced by storms with effective rainfall duration less than the time of concentration. Therefore, they resemble subconcentrated catchment flow, albeit with the addition of a small but perceptible amount of diffusion. El efecto neto de la difusión de la escorrentía es reducir las tasas de flujo a niveles inferiores a los que podrían ser alcanzados sólo por convección. En la práctica, la difusión actúa para suavizar la respuesta de captación. La función de respuesta resultante es generalmente continua, y se conoce como el hidrograma de caudales, hidrograma de escorrentía, o simplemente el hidrograma. Hidrogramas típicos de una sola tormenta tienen una forma similar a la mostrada en la Fig. 2-58. Por lo general, son producidos por tormentas con precipitaciones duración efectiva menor que el tiempo de la concentración. Por lo tanto, se asemejan a flujo de captación subconcentrated, aunque con la adición de una pequeña pero perceptible cantidad de difusión. Fig. 2-58  Hidrograma de una sola tormenta típica. The various elements in a typical single-storm hydrograph are shown in Fig. 2- 59. The zero time (or starting time) depicts the beginning of the hydrograph. The hydrograph peak describes the maximum flow rate. The time-to-peak is measured from zero time to the time at which the peak flow is attained. The rising limb is the part of the hydrograph between zero time and time-to-peak. The recession (or receding limb) is the part of the hydrograph between time-to-peak and time base. The time base is measured from zero time to a time defining the end of the recession. The recession is logarithmic in nature, approaching zero flow in an asymptotic way. For practical applications, the end of the recession is usually defined in an arbitrary manner. The point of inflection of the receding limb is the point corresponding to zero curvature. The hydrograph volume is obtained by integrating the flow rates from zero time to time base. Los diversos elementos en un hidrograma típico de un solo tormenta se muestran en la Fig. 2- 59. El (tiempo o de partida) el tiempo cero representa el inicio de la hidrograma. El pico hidrograma describe la tasa de flujo máximo. El pico de tiempo-a-se mide desde el tiempo cero hasta el momento en que se alcanza el pico de flujo. La rama ascendente es la parte del hidrograma entre el tiempo y el tiempo de salida a pico cero. La recesión (o la integridad física del retroceso) es la parte del hidrograma entre el tiempo de salida al pico y la base de tiempo. La base de tiempo se mide desde el tiempo cero a un tiempo que define el extremo de la recesión. La recesión es logarítmica en la naturaleza, acercándose a flujo cero de forma asintótica. Para aplicaciones prácticas, el final de la recesión se define generalmente de una manera arbitraria. El punto de inflexión de la extremidad del retroceso es el punto que corresponde a la curvatura cero. El volumen hidrograma se obtiene mediante la integración de las velocidades de flujo desde el tiempo cero a base de tiempo. Fig. 2-59  Elementos del hidrograma de una sola tormenta. The shape of the hydrograph, showing a positive skew, with recession time greater than rising time, is caused by the essentially different responses of surface flow, interflow, and groundwater flow. Indeed, the runoff hydrograph can be thought of as consisting of the sum of up to three hydrographs, as shown in Fig. 2-60 (a). The fast and peaked hydrograph is produced by surface flow while the other two are the result of interflow and groundwater flow. The superposition of these hydrographs results in a runoff hydrograph exhibiting a long tail (positive skew), as depicted in Fig. 2-60 (b). La forma de la hidrograma, mostrando un sesgo positivo, con el tiempo recesión mayor que el aumento de tiempo, es causada por los esencialmente diferentes respuestas de flujo de superficie, interflujo, y el flujo de las aguas subterráneas. De hecho, el hidrograma de escorrentía puede ser pensado como un conjunto de la suma de hasta tres hidrogramas, como se muestra en la Fig. 2-60 (a). El hidrograma rápido y alcanzó su punto máximo se produce por el flujo de superficie, mientras que los otros dos son el resultado de interflujo y subterráneas flujo. La superposición de estos hidrogramas se traduce en un hidrograma de escorrentía exhibiendo una larga cola (sesgo positivo), como se muestra en la Fig. 2-60 (b). Fig. 2-60  Los componentes del hidrograma de escurrimiento. The feature of positive skew allows the definition of a few additional geometric hydrograph properties. The time-to-centroid tg is measured from zero time to the time separating the hydrograph into two equal volumes (Fig. 2-61). The volume-to-peak Vp is obtained by integrating the flow rates from zero time to time-to-peak. In synthetic unit hydrograph analysis, the ratio of volume-to-peak to hydrograph volume is used as a measure of hydrograph shape (Chapter 5). La característica de asimetría positiva permite la definición de algunas propiedades geométricas hidrograma adicionales. La tg-time-to centroide se mide desde el tiempo cero hasta el tiempo que separa el hidrograma en dos volúmenes iguales (Fig. 2 hasta 61). El volumen a pico Vp se obtiene mediante la integración de las velocidades de flujo desde tiempo cero hasta el tiempo de salida a pico. En el análisis hidrograma unitario sintético, la relación del volumen a pico al volumen hidrograma se utiliza como una medida de forma hidrograma (Capítulo 5). Fig. 2-61  Propiedades del hidrograma de una sola tormenta. Hydrographs of perennial streams may include substantial amounts of baseflow. The separation of runoff into direct runoff (surface flow) and indirect runoff (baseflow) can be accomplished by resorting to one of several hydrograph separation techniques (Chapter 5). These techniques can also be used in the analysis of multiple-storm hydrographs, which typically exhibit two or more peaks and valleys. Hidrogramas de arroyos perennes pueden incluir cantidades sustanciales de caudal base. La separación de la escorrentía en escorrentía directa (flujo superficial) y la escorrentía indirecta (flujo de base) se puede lograr recurriendo a una de varias técnicas de separación hidrograma (Capítulo 5). Estas técnicas también se pueden utilizar en el análisis de hidrogramas de múltiples tormenta, que típicamente exhiben dos o más picos y valles. Analytical Hydrographs. Analytical expressions for streamflow hydrographs are sometimes used in hydrologic studies. The simplest formula is based on either a sine or cosine function. These, however, have zero skew (Chapter 6) and therefore do not properly describe the shape of natural hydrographs. Hidrogramas Analítica. Expresiones analíticas para hidrogramas de caudal se utilizan a veces en estudios hidrológicos. La fórmula más simple se basa en ya sea una función seno o coseno. Estos, sin embargo, tienen cero sesgo (capítulo 6) y por lo tanto no describen adecuadamente la forma de hidrogramas naturales. An analytical hydrograph that is often used to simulate natural hydrographs is the gamma function, expressed as follows: Un hidrograma analítico que se utiliza a menudo para simular hidrogramas naturales es la función gamma, expresó de la siguiente manera:                                            t Q  =  Qb  +  (Qp  -  Qb ) [ _____ ] m  e (tp - t ) / (tg - tp )                                           tp (2-64) in which Q = flow rate; Qb = baseflow; Qp = peak flow; t = time; tp = time-to-peak; tg = time-to-centroid; and m = tp /(tg - tp). For values of tg greater than tp, Eq. 2-64 exhibits positive skew. en la que Q = caudal; Qb = flujo de base; Qp = caudal pico; t = tiempo; tp = tiempo a pico; tg = tiempo de llegada al centro de gravedad; ym = tp / (tg - tp). Para valores de tg mayor que tp, Eq. 2-64 exhibe sesgo positivo. Example 2-11. / Ejemplo 2-11. Use Eq. 2-64 to calculate streamflow hydrograph ordinates at hourly intervals, with the following data: Qb = 100 m3/s; Qp = 500 m3/s; tp = 3 h; and tg = 4.5 h. Utilice la ecuación. 2-64 para calcular coordenadas hidrograma de caudales en intervalos de una hora, con los siguientes datos: Qb = 100 m3 / s; Qp = 500 m3 / s; tp = 3 h; y tg = 4,5 h. The application of Eq. 2-64 leads to: La aplicación de la ecuación. 2-64 conduce a:                                   t Q  =   100  +  400 [ _____ ] 2  e (3 - t ) / 1.5                                   3 The hydrograph ordinates at hourly intervals are shown in Tabla 2-11. It is seen that the flow rate at t = 0 is 100 m3/s, it reaches a peak of 500 m3/s at t = 3 h, and it recedes back to 103 m3/s at t = 15 h. Las ordenadas hydrograph en intervalos de una hora se muestran en la Tabla 2-11. Se ve que la velocidad de flujo en t = 0 es de 100 m3 / s, que alcanza un pico de 500 m3 / s en t = 3 h, y se aleja de nuevo a 103 m3 / s en t = 15 h. Tabla 2-11  Calculated gamma hydrograph ordinates: Example 2-11. / Calculado gamma ordenadas hidrograma: Ejemplo 02.11. Time (h) / Tiempo (h) Flow (m3/s) / Flujo (m3/s) 0 100 1 269 2 446 3 500 4 465 5 393 6 317 7 251 8 201 9 166 10 142 11 126 12 116 13 110 14 106 15 103 Flow in Stream Channels / Flujo en Canales Stream Streamflow hydrographs flow in stream channels that are carved on the land surface. The following properties are used to describe stream channels: Hidrogramas de caudal de flujo en canales de la corriente que están tallados en la superficie de la tierra. Las siguientes propiedades se utilizan para describir canales de la corriente: Cross-sectional dimensions, Dimensiones transversales, Cross-sectional shape, Forma en sección transversal, Longitudinal slope, and Pendiente longitudinal y Boundary friction. / Fricción de Límites. The channel cross section has the following geometric and hydraulic elements: (a) flow area, (b) top width, (c) wetted perimeter, (d) hydraulic radius, (e) hydraulic depth, and (f) aspect ratio. The flow area A is the area of the cross section occupied by the flow. The top width T is the channel width at the elevation of the water surface. The wetted perimeter P is the perimeter of the flow area in direct contact with the land. The hydraulic radius R is the ratio of flow area to wetted perimeter: R = A/P. The hydraulic depth D is the ratio of flow area to top width: D = A/T. The aspect ratio, a measure of cross-sectional shape, is the ratio of top width to hydraulic depth (T/D). La sección transversal del canal tiene los siguientes elementos geométricos e hidráulicos: (a) la zona de flujo, (b) ancho de la parte superior, (c) perímetro mojado, (d) el radio hidráulico, (e) la profundidad hidráulica, y (f) la relación de aspecto. El área de flujo A es el área de la sección transversal ocupada por el flujo. El ancho de la parte superior T es el ancho del canal en la elevación de la superficie del agua. El perímetro P humedecida es el perímetro del área de flujo en contacto directo con la tierra. El radio hidráulico R es la relación de área de flujo para perímetro mojado: R = A / P. La profundidad hidráulico D es la relación de área de flujo a la anchura de la parte superior: D = A / T. La relación de aspecto, una medida de la forma en sección transversal, es la relación de la anchura superior a la profundidad hidráulica (T / D). Channel top widths vary widely, ranging from a few meters for small mountain streams to several kilometers for very large rivers. Mean flow depths range from as low as a fraction of a meter for small mountain streams to more than 50 m for very large rivers. [The maximum depth of the Amazon river, the largest in the world, is close to 90 m]. Aspect ratios vary widely in nature; however, most streams and rivers have aspect ratios in excess of 10. Very wide streams (e.g., braided streams) may have aspect ratios exceeding 100. Top anchos de canal varían ampliamente, que van desde unos pocos metros para los pequeños arroyos de montaña a varios kilómetros de grandes ríos. La media de las profundidades de flujo van desde un mínimo de una fracción de un metro para los pequeños arroyos de montaña a más de 50 m para los muy grandes ríos. [La profundidad máxima del río Amazonas, el más grande del mundo, está cerca de 90 m]. Relaciones de aspecto varían ampliamente en la naturaleza; Sin embargo, la mayoría de los arroyos y ríos tienen relaciones de aspecto superiores a 10. arroyos muy anchos (por ejemplo, corrientes trenzadas) pueden tener relaciones de aspecto superiores a 100. The longitudinal channel slope is the change in elevation with distance. The mean bed elevation is generally used to calculate channel slope. For short reaches or mild slopes, slope calculations may be hampered by the difficulty of accurately establishing the mean bed elevation. A practical alternative is to use the water surface slope as a measure of channel slope. The water surface slope, however, varies in space and time as a function of the flow nonuniformity and unsteadiness. The steady equilibrium (i.e., uniform) water surface slope is usually taken as a measure of channel slope. Therefore, mean bed slope and steady equilibrium water surface slope are often treated as synonymous. Generally, the longer the channel reach, the more accurate the determination of channel slope. La pendiente longitudinal del canal es el cambio en la elevación con la distancia. La elevación de cama media generalmente se utiliza para calcular la pendiente del canal. Por tramos cortos o pendientes suaves, cálculos de la pendiente pueden ser obstaculizadas por la dificultad de establecer con precisión la elevación cama media. Una alternativa práctica es utilizar la pendiente de la superficie del agua como una medida de pendiente del canal. La pendiente de la superficie del agua, sin embargo, varía en el espacio y el tiempo como una función de la falta de uniformidad de flujo y la inestabilidad. El equilibrio constante (es decir, uniforme) pendiente de la superficie del agua se suele tomar como medida de la pendiente del canal. Por lo tanto, significan pendiente del lecho y la pendiente de la superficie de agua de equilibrio estable se tratan a menudo como sinónimos. Generalmente, cuanto mayor sea el alcance de canal, más precisa será la determinación de la pendiente del canal. Boundary friction refers to the type and dimensions of the particles lining the channel cross section below the waterline. In alluvial channels, geomorphic bed features such as ripples and dunes may represent a substantial contribution to the overall friction (Chapter15). Particles lying on the channel bed may range from large boulders for typical mountain streams (Fig. 2-62) to silt particles in the case of large tidal rivers. Fricción límite se refiere al tipo y dimensiones de las partículas que recubren la sección transversal del canal por debajo de la línea de flotación. En canales aluviales, las características geomorfológicas de la cama como ondulaciones y dunas pueden representar una contribución sustancial a la fricción global (Capítulo 15). Las partículas que mienten en el lecho del canal pueden variar de grandes rocas de los arroyos de montaña típicas (Fig. 2-62) para el limo partículas en el caso de los grandes ríos de marea. Fig. 2-62  Flow in a mountain stream. / El flujo en un arroyo de montaña. For small streams, particles on the channel banks may be as large as the particles on the bottom. River banks, however, are likely to consist of particles of much varied size than those on the channel bottom. The high aspect ratio of rivers generally results in the banks contributing only a small fraction of the total boundary friction. Therefore, the boundary friction is often taken as synonymous with bed or bottom friction. Para los pequeños arroyos, las partículas en las orillas de los canales pueden ser tan grandes como las partículas en la parte inferior. Bancos del río, sin embargo, es probable que consisten en partículas de gran tamaño variados que los de la parte inferior del canal. La alta relación de aspecto de los ríos generalmente resulta en los bancos que contribuyen sólo una pequeña fracción de la fricción total de frontera. Por lo tanto, la fricción límite se toma a menudo como sinónimo de la cama o la fricción del fondo. Uniform flow formulas. Flow in streams and rivers is evaluated by using empirical formulas such as the Manning or Chezy equations. The Manning formula is: Fórmulas de flujo uniforme. Flujo en los arroyos y ríos se evalúa mediante el uso de fórmulas empíricas, como las ecuaciones de Manning o Chezy. La fórmula de Manning es:             1 V  =  _____ R 2/3 S 1/2             n (2-65) in which V = mean flow velocity, in meters per second; R = hydraulic radius, in meters; S = channel slope, in meters per meter; and n = Manning friction coefficient. In U.S. customary units, with V in feet per second, R in feet, and S in feet per foot, the right side of Eq. 2-65 is multiplied by the constant 1.486. en la que V = velocidad media de flujo, en metros por segundo; R = radio hidráulico, en metros; S = pendiente del canal, en metros por metro; y Manning n = coeficiente de fricción. En Estados Unidos las unidades habituales, con V en pies por segundo, R en los pies, y S en pies por pie, el lado derecho de la ecuación. 2-65 se multiplica por la constante de 1.486. In natural channels, n can take values as low as 0.02 and as high as 0.2 in some unusually high roughness cases (e.g., flood plains adjacent to rivers). A good working value for a clean, straight, full-stage stream of fairly uniform cross section is 0.03. Typical n values for natural streams and rivers are in the range 0.03-0.05. En los canales naturales, n puede tomar valores tan bajos como 0.02 y de hasta 0,2 en algunos casos de rugosidad inusualmente altas (por ejemplo, las llanuras de inundación adyacentes a ríos). Una buena relación de trabajo para una recta corriente limpia, de una etapa llena de sección transversal bastante uniforme es 0,03. N valores típicos para las corrientes naturales y ríos están en el rango desde 0,03 hasta 0,05. A U.S. Geological Survey study [4] has documented n values for natural streams ranging from as low as n = 0.024 for the Columbia River at Vernita, Washington (a large river with streambanks largely devoid of vegetation) [(Fig. 2-63 (a)], to as high as n = 0.079 for Cache Creek near Lower Lake, California (a small stream with large, angular boulders in the bed, and exposed rocks, boulders, and trees in the banks) [(Fig. 2-63 (b)]. Un estudio Geológico de Estados Unidos [4] ha documentado valores de n para los flujos naturales que van desde un mínimo de n = 0.024 para el río Columbia en Vernita, Washington (un gran río con arroyos gran parte desprovistas de vegetación) [(fig. 2-63 (a)], hasta un máximo de n = 0.079 para Cache Creek cerca de Lower Lake, California (un pequeño arroyo con grandes piedras angulares en la cama, y rocas expuestas, rocas y árboles en las orillas) [(Fig. 2- 63 (b)]. Fig. 2-63 (a)  Columbia River at Vernita, Washington. / Río Columbia en Vernita, Washington. Fig. 2-63 (b)  Cache Creek near Lower Lake, California. / Cache Creek cerca de Lower Lake, California. The Chezy equation is La ecuación es Chezy V  =  C R 1/2 S 1/2 (2-66) in which C = Chezy coefficient, in m1/2 s-1; and other terms are the same as for Eq. 2-65. Chezy coefficients equivalent to the preceding conditions range from about 80 m1/2 s-1 for large rivers to about 10 m1/2 s-1 for small streams. Typical C values for natural streams and rivers are in the range 25-50 m1/2 s-1. en el que el coeficiente C = Chezy, en m1 / 2 s-1; y otros términos son los mismos que para la ecuación. 2-65. Coeficientes Chezy equivalentes a las condiciones anteriores van desde unos 80 m1 / 2 s-1 para los grandes ríos a cerca de 10 m1 / 2 s-1 para los pequeños arroyos. Los valores típicos C para corrientes naturales y ríos están en el rango de 25-50 m1 / 2 s-1. Equation 2-66 can be expressed in dimensionless form as follows: Ecuación 2-66 se puede expresar en forma adimensional como sigue:               C V  =  _______ g 1/2 R 1/2 S 1/2             g 1/2 (2-67) in which g = gravitational acceleration, and C/g1/2 = dimensionless Chezy coefficient. Dimensionless Chezy coefficients equivalent to the preceding conditions range from 25.5 for large rivers to 3.2 for small streams. Typical values for natural streams and rivers are in the range 8-16. en la que g = aceleración de la gravedad, y C / g1 / 2 = coeficiente adimensional Chezy. Coeficientes Chezy sin dimensiones equivalentes a las condiciones anteriores van desde 25,5 por grandes ríos a 3,2 para los pequeños arroyos. Los valores típicos para las corrientes naturales y ríos están en el rango 8-16. For certain applications, Eq. 2-67 can be readily transformed into a formula with an enhanced physical meaning. For hydraulically wide channels, i.e., those with aspect ratio greater than 10, the top width and wetted perimeter can be assumed to be approximately the same. This implies that the hydraulic depth (D) can be substituted for the hydraulic radius (R), leading to: Para ciertas aplicaciones, la Ec. 2-67 se puede transformar fácilmente en una fórmula con un significado físico mejorado. Para los canales de ancho hidráulicamente, es decir, aquellos con una relación de aspecto mayor que 10, la anchura de la parte superior y perímetro mojado se puede suponer que ser aproximadamente la misma. Esto implica que la profundidad hidráulico (D) puede ser sustituido por el radio hidráulico (R), que conduce a: S  =  f F 2 (2-68) in which f = a dimensionless friction factor equal to f = g/C 2, and F = Froude number, equal to F = V / (gD)1/2. It can be shown that the friction factor in Eq. 2-68 is equal to one-eight (1/8) of the Darcy-Weisbach friction factor fD used in the hydraulics of closed conduits. Dimensionless friction factors equivalent to the preceding conditions range from 0.0016 for large rivers to 0.097 for small streams. Typical values for natural streams and rivers are in the range 0.004-0.016. en el que f = factor adimensional de fricción igual a f = g / C 2, y el número F = Froude, igual a F = V / (gD) 1/2. Se puede demostrar que el factor de fricción en la Ec. 2-68 es igual a ocho (1/8) del factor de fricción de Darcy-Weisbach fD utilizado en el sistema hidráulico de conductos cerrados. Factores de fricción sin dimensiones equivalentes a las condiciones anteriores van desde 0,0016 para grandes ríos a 0,097 para los pequeños arroyos. Los valores típicos de arroyos naturales y ríos están en el rango de 0,004 a 0,016. Equation 2-68 states that for hydraulically wide channels, the channel slope is proportional to the square of the Froude number, with the friction factor f as the proportionality coefficient. In practice, Eq. 2-68 be used as a convenient predictor of any of these three dimensionless parameters, once the other two are known. Furthermore, it implies that if one of the three parameters is kept constant, a change in one of the other two causes a corresponding change in the third. Ecuación 2-68 establece que para los canales de ancho hidráulicamente, la pendiente del canal es proporcional al cuadrado del número de Froude, con el factor de fricción f como el coeficiente de proporcionalidad. En la práctica, la Ec. 2-68 ser utilizado como un predictor conveniente de cualquiera de estos tres parámetros adimensionales, una vez que los otros dos son conocidos. Además, esto implica que si uno de los tres parámetros se mantiene constante, un cambio en uno de los otros dos provoca un cambio correspondiente en la tercera. Notwithstanding the theoretical appeal of Eqs. 2-66 and 2-68, the Manning equation has had wider acceptance in practice. This is attributed to the fact that in natural channels, the Chezy coefficient is not constant, tending to increase with hydraulic radius. The comparison of Eqs. 2-65 and 2-66 leads to: A pesar de lo atractivo teórico de las ecuaciones. 2-66 y 2-68, la ecuación de Manning ha tenido mayor aceptación en la práctica. Esto se atribuye al hecho de que en los canales naturales, el coeficiente de Chezy no es constante, que tiende a aumentar con el radio hidráulico. La comparación de las ecuaciones. 2-65 y 2-66 conduce a:             1 C  =  _____ R 1/6             n (2-69) Equation 2-69 implies that, unlike Chezy C, Manning n is a constant. Experience has shown, however, that at a given cross-section, n may vary with discharge and stage (Fig. 2-64). Moreover, as stage varies from low to high, alluvial rivers can move their beds and generate/erase ripples and dunes, increasing/decreasing channel friction (Chapter 15). Ecuación 2-69 implica que, a diferencia de Chezy C, Manning n es una constante. La experiencia ha demostrado, sin embargo, que en una sección transversal dada, n puede variar con la descarga y la etapa (Fig. 2-64),. Además, como etapa varía de baja a alta, ríos aluviales pueden mover sus camas y generar / borrar ondulaciones y dunas, aumentar / disminuir la fricción canal (Capítulo 15). Fig. 2-64  A large river overflowing onto the adjacent flood plain (Mato Grosso, Brazil). / Un gran río desbordado en la llanura de inundación adyacente (Mato Grosso, Brasil). River Stages. At any location along a river, the river stage is the elevation of the water surface above a given datum. This datum can be either an arbitrary one or the NAVD (North American Vertical Datum), a standard measure of mean sea level. Etapas River. En cualquier ubicación a lo largo de un río, el nivel del río es la elevación de la superficie del agua encima de una referencia dada. Este dato puede ser arbitraria o la NAVD (North American Datum vertical), una medida estándar de nivel medio del mar. River stages are a function of flow rate. Flow rates can be grouped into: (1) low flow, (2) average flow, and (3) high flow. Low flow is typical of the dry season, when streamflow is largely composed of baseflow originating mostly in contributions from groundwater flow. High flow occurs during the wet season, when streamflow is primarily due to contributions from surface runoff. Average flow usually occurs midseason and may have mixed contributions from surface runoff, interflow, and groundwater flow. Etapas de río son una función de la velocidad de flujo. Las velocidades de flujo se pueden agrupar en: (1) de bajo flujo, (2) flujo de la media, y (3) de alto flujo. Bajo flujo es típico de la estación seca, cuando el caudal se compone en gran medida de caudal base origina principalmente en las contribuciones de flujo de agua subterránea. Alto flujo se produce durante la temporada de lluvias, cuando el caudal se debe principalmente a las contribuciones de la escorrentía superficial. Caudal medio por lo general ocurre a mitad de temporada y puede tener contribuciones mixtas de la escorrentía superficial, subsuperficial, y el flujo de las aguas subterráneas. Low flows studies are necessary when determining minimum flow rates, below which a certain use would be impaired. Examples of such uses are irrigation requirements, hydropower generation, and minimum instream flows needed for fisheries protection and compliance with water pollution regulations. Excessive use of groundwater may lead to baseflow losses; thus, Increasingly, surface runoff studies are focusing on baseflow and low flows. Estudios bajos flujos son necesarios para determinar los caudales mínimos, por debajo del cual un determinado uso podría verse afectada. Ejemplos de tales usos son los requisitos de riego, generación de energía hidroeléctrica, y caudales ecológicos mínimos necesarios para la protección de la pesca y el cumplimiento de la normativa de contaminación del agua. El uso excesivo de agua subterránea puede conducir a pérdidas de caudal base; por lo tanto, cada vez más, los estudios de escorrentía superficiales se están centrando en el caudal base y caudales bajos. Average flows play an important role in the calculation of monthly and annual volumes available for storage and use. Applications are usually found in connection with the sizing of storage reservoirs. Promedio de flujos juegan un papel importante en el cálculo de los volúmenes mensuales y anuales disponibles para almacenamiento y uso. Las solicitudes se encuentran generalmente en relación con el tamaño de los depósitos de almacenamiento. High flow studies are related to the floods and flood hydrology. Typically, during high flows, natural streams and rivers have the tendency to overflow their banks, with stages reaching above bank-full stage. In such cases, the flow area includes a portion of the land located adjacent to the river, on one or both sides. In alluvial valleys, the land that is subject to inundation during periods of high flow is referred to as the flood plain (Fig. 2-65). The evaluation of high flows is necessary for flood forecasting, flood control, and flood mitigation. Estudios de alto flujo están relacionados con las inundaciones y la hidrología de inundaciones. Típicamente, durante flujos altos, arroyos y ríos naturales tienen la tendencia a desbordar sus bancos, con etapas de llegar por encima de escenario al banco completo. En tales casos, el área de flujo incluye una porción de la tierra situada adyacente al río, en uno o ambos lados. En los valles aluviales, la tierra que está sujeta a inundaciones durante los períodos de alto flujo se conoce como la llanura de inundación (Fig. 2-65). La evaluación de flujos altos es necesaria para la previsión de inundaciones, control de inundaciones y mitigación de inundaciones. Fig. 2-65  Flood plain flooding (Mato Grosso, Brazil). / Flood inundaciones llanura (Mato Grosso, Brasil). Rating Curves. It is known that river stage varies as a function of discharge, but the exact nature of the relationship is not readily apparent. Given a long and essentially prismatic channel reach, a single-valued relationship between stage and discharge at a cross section defines the equilibrium rating curve. For steady uniform flow, the rating curve is unique, i.e., there is a single value of stage for each value of discharge and vice versa (Fig. 2-66). In this case, the equilibrium rating curve can be calculated with either the Manning or Chezy equations. In open-channel hydraulics, this property of uniqueness of the rating qualifies the channel reach as a channel control. Curvas de calificación. Se sabe que la etapa de río varía como una función de descarga, pero la naturaleza exacta de la relación no es fácilmente evidente. Dada una larga y esencialmente prismática alcance del canal, una relación unívoca entre el escenario y descarga en una sección transversal define la curva de equilibrio. Para el flujo uniforme constante, la curva de calificación es único, es decir, existe un único valor de fase para cada valor de la descarga y viceversa (Fig. 2-66). En este caso, la curva de equilibrio se puede calcular con cualquiera de las ecuaciones de Manning o Chezy. En la hidráulica de canales abiertos, esta propiedad de la singularidad de la calificación califica el alcance canal como un control de canal. Fig. 2-66  Una curva de gasto típica. However, other flow conditions, specifically nonuniformity (gradually varied steady flow) and unsteadiness (e.g., gradually varied unsteady flow), can cause deviations from the steady equilibrium rating. These deviations are less tractable. In particular, flood wave theory justifies the presence of a loop in the rating, as shown in Fig. 2067. Intuitively, the rising limb of the flood-wave hydrograph has a steeper water surface slope than that of equilibrium flow, leading to greater flows and lower stages. Conversely, the receding limb has a milder water surface slope, resulting in smaller flows and higher stages; thus the rationale for the loop's presence. The loop effect, however, is likely to be small and is usually neglected on practical grounds. Where increased accuracy is required, unsteady flow modeling can be used to account for the looped rating (Chapter 9). Sin embargo, otras condiciones de flujo, específicamente no uniformidad (varió gradualmente flujo constante) y la inestabilidad (por ejemplo, gradualmente variado flujo no permanente), puede causar desviaciones de la calificación de equilibrio estable. Estas desviaciones son menos manejable. En particular, la teoría de onda de crecida justifica la presencia de un bucle en la calificación, como se muestra en la Fig. 2067. Intuitivamente, la rama ascendente del hidrograma de onda de inundación tiene una inclinación de la superficie del agua más pronunciado que el de flujo de equilibrio, lo que lleva a mayores flujos y etapas inferiores. Por el contrario, la extremidad del retroceso tiene una pendiente más suave la superficie del agua, dando lugar a flujos más pequeños y etapas superiores; por lo tanto la razón de la presencia del bucle. El efecto de bucle, sin embargo, es probable que sea pequeña y por lo general se descuida por motivos prácticos. Cuando se requiere una mayor precisión, el modelado de flujo no permanente se puede utilizar para dar cuenta de la calificación de bucle (capítulo 9). Fig. 2-67  Una curva de bucle. Two other processes related to sedimentation have a bearing in the evaluation of stage-discharge relations: (1) the short-term effects, and (2) long-term effects. The short-term effects are due to the fact that the amount of boundary friction varies with flow rate. Rivers flowing on loose boundaries composed of gravel, sand, and silt constantly try to minimize their changes in stage. This is accomplished through the following mechanism: During low flow, the bed friction consists not only of grain friction but also of form friction, caused by bed features such as ripples and dunes (Chapter 15). During high flows, the swiftness of the current acts to obliterate the bed features, reducing form friction to a minimum, essentially with only grain friction remaining. The reduced friction during high flows gives rivers the capability to carry a greater discharge for a given stage. This explains the demonstrated shift from low-flow rating to high-flow rating in natural river channels (Fig. 2-63). Otros dos procesos relacionados con la sedimentación tienen una influencia en la evaluación de las relaciones nivel-caudal: efectos (1) a corto plazo, y (2) los efectos a largo plazo. Los efectos a corto plazo son debidos al hecho de que la cantidad de fricción límite varía con la velocidad de flujo. Los ríos que fluyen en los límites sueltas compuestas de grava, arena y limo constantemente tratan de minimizar sus cambios en el escenario. Esto se logra a través del siguiente mecanismo: Durante bajo caudal, la fricción cama consiste no sólo en la fricción del grano, sino también de forma fricción, causada por las características de la cama como ondulaciones y dunas (Capítulo 15). Durante flujos altos, la velocidad de la corriente actúa para destruir las características de la cama, lo que reduce la fricción forma a un mínimo, esencialmente sólo con fricción grano restante. La fricción reducida durante los fuertes flujos de ríos da la capacidad para llevar una descarga mayor para una etapa determinada. Esto explica el cambio demostrado de calificación de bajo flujo a la calificación de alto flujo en los canales fluviales naturales (Fig. 2-63). The long-term sedimentation effect is due to the fact that rivers continuously subject their boundaries to recurring cycles of erosion and deposition, depending on the sediment load they carry (Chapter 15). Some very active rivers may be eroding; others may be aggrading. Moreover, some geomorphologically active rivers may substantially change their cross sections during major floods. Invariably, shifts in rating are the net result of these natural geomorphic processes. El efecto de sedimentación a largo plazo es debido al hecho de que los ríos someten continuamente sus límites a los ciclos de erosión y deposición recurrentes, dependiendo de la carga de sedimentos que llevan (Capítulo 15). Algunos ríos muy activos pueden estar erosionando; otros pueden ser de agradación. Por otra parte, algunos ríos geomorfológicamente activos pueden cambiar sustancialmente sus secciones transversales durante las grandes inundaciones. Invariablemente, los cambios en la calificación son el resultado neto de estos procesos geomorfológicos naturales. Rating Curve Formulas. In spite of the apparent complexities, rating curves are a useful and practical tool in hydrologic analysis, allowing the direct conversion of stage to discharge and vice versa. Discharge can be obtained from the rating by the simple procedure of measuring the stage. Conversely, if discharge is known, for instance, at a catchment outlet, stage at the outlet can be readily determined from a suitable rating. Fórmulas Clasificación curva. A pesar de las complejidades aparentes, curvas de gasto son una herramienta útil y práctica en el análisis hidrológico, lo que permite la conversión directa de la etapa de descargar y viceversa. Discharge se puede obtener de la calificación por el simple procedimiento de medición de la etapa. A la inversa, si se conoce la descarga, por ejemplo, en una toma de corriente de captación, la etapa en la salida se puede determinar fácilmente a partir de una clasificación adecuada. There are several ways to determine an equation for the rating. Invariably, they are based on curve-fitting stage-discharge data. A widely used equation is the following [45]: Hay varias formas para determinar una ecuación para la calificación. Invariablemente, que se basan en datos de nivel-caudal de ajuste de curvas. Una ecuación muy utilizado es el siguiente [45]: Q  =  a (h - ho ) b (2-70) in which Q = discharge; h = gage height; ho = reference height; and a and b are constants. Several values of reference height are tried. The proper value of reference height is that which makes the stage-discharge data plot as close as possible to a straight line on logarithmic paper. Subsequently, the values of the constants a and b are determined by regression analysis (Chapter 7). en la que Q = descarga; h = altura del medidor; ho = altura de referencia; y a y b son constantes. Varios valores de altura de referencia son juzgados. El valor apropiado de altura de referencia es la que hace que la trama de datos altura-caudal lo más cerca posible a una línea recta en papel logarítmico. Posteriormente, los valores de las constantes a y b se determinan por análisis de regresión (Capítulo 7). Streamflow Variability / La variabilidad de caudales The study of streamflow variability is the cornerstone of engineering hydrology. Streamflow and river flow vary not only seasonally, but also annually, multiannually, and with climate and geographic location. Global climate change may also affect streamflow variability. Over the long term, the total amount of streamflow is directly related to the amount of environmental moisture, i.e., the moisture present in soil and air. The inland advection of water vapor supplies the moisture which eventually constitutes precipitation. Whether this moisture reaches the catchment outlet remains to be determined by further analysis. El estudio de la variabilidad del caudal es la piedra angular de la hidrología de la ingeniería. Caudal y caudal del río no sólo varían estacionalmente, sino también anualmente, multiannually, y con el clima y la ubicación geográfica. El cambio climático global también puede afectar la variabilidad del caudal. En el largo plazo, la cantidad total de caudal está directamente relacionada con la cantidad de humedad ambiental, es decir, la humedad presente en el suelo y el aire. La advección hacia el interior de vapor de agua proporciona la humedad que finalmente constituye precipitación. Si esta humedad alcanza la salida de captación queda por determinar por su posterior análisis. On an average global basis, mean annual runoff, measured at the mouths of peripheral continental basins, amounts to about 39 percent of total precipitation. Most of the remainder, about 59 percent, is accounted for by the long-term abstractive processes of evaporation and evapotranspiration, which include evaporation from water bodies, evaporation from soil and bare ground, and evapotranspiration from vegetation. A small percentage, about 2 percent, percolates deep enough into the ground to bypass the surface waters, eventually discharging into the ocean (Fig. 2-68). Sobre una base media global, la escorrentía media anual, medido en las desembocaduras de las cuencas continentales periféricos, asciende a cerca del 39 por ciento de la precipitación total. La mayor parte del resto, alrededor del 59 por ciento, se explica por los procesos abstractivos a largo plazo de la evaporación y la evapotranspiración, que incluyen la evaporación de los cuerpos de agua, la evaporación del suelo y el suelo desnudo, y la evapotranspiración de la vegetación. Un pequeño porcentaje, alrededor del 2 por ciento, se filtra lo suficientemente profundo en el suelo para evitar las aguas superficiales, con el tiempo de descarga en el océano (Fig. 2-68). Fig. 2-68  Componentes globales promedio del balance hídrico. Seasonal Variability. A typical catchment in a subhumid region may show runoff rates and volumes varying throughout the year, with a tendency to low flows during the dry season and high flows during the wet season. However, a catchment in a more extreme climate will show a quite different behavior. In the ephemeral streams typical of arid regions, runoff is nonexistent during periods of no precipitation; for these streams, runoff occurs only in direct response to precipitation. On the other hand, in humid and extremely humid climates, rivers show substantial amounts of runoff throughout the year, with relatively little variability between the seasons. Variabilidad estacional. Una cuenca típica en una región subhúmeda puede mostrar tasas de escorrentía y los volúmenes que varían a lo largo del año, con una tendencia a flujos bajos durante la estación seca y los altos flujos durante la estación húmeda. Sin embargo, una cuenca en un clima más extremo mostrará un comportamiento muy diferente. En los arroyos efímeros típicos de las regiones áridas, la escorrentía es inexistente durante los períodos de ausencia de precipitación; de estas corrientes, la escorrentía se produce sólo en respuesta directa a la precipitación. Por otro lado, en climas húmedos y muy húmedos, ríos muestran cantidades sustanciales de escorrentía a lo largo del año, con relativamente poca variabilidad entre las estaciones. The reason for the seasonal variability of streamflow lies in the relative contributions of direct (surface flow) and indirect runoff (baseflow). In subhumid regions, indirect runoff is a small, but nevertheless measurable, fraction of total runoff. On the other hand, in arid regions, particularly for ephemeral streams, indirect runoff is either zero or negligible. Furthermore, in humid regions, indirect runoff is substantial throughout the year, often being a sizable fraction of total runoff. La razón de la variabilidad estacional de caudal se encuentra en las contribuciones relativas de (flujo superficial) y la escorrentía directa indirecta (flujo de base). En las regiones subhúmedas, escorrentía indirecta es una pequeña, pero sin embargo, medible, fracción de escorrentía total. Por otro lado, en las regiones áridas, en particular para los flujos efímeros, la escorrentía indirecto es cero o insignificante. Por otra parte, en las regiones húmedas, la escorrentía indirecta es importante durante todo el año, siendo a menudo una fracción considerable de escorrentía total. The phenomenon described above can be further explained in the following way: Groundwater reservoirs act to store large amounts of water, which are slowly transported to lower elevations. The bulk of this water (about 98% on a global basis) is eventually released back to the surface waters. With seepage being the dominant process, the flow of groundwater is slow and, therefore, subject to a substantial amount of diffusion. The net effect is that of a permanent contribution from groundwater to surface water in the form of baseflow, or the dry-weather flow of rivers (Fig. 2-69). To evaluate the seasonal variability of streamflow, it is therefore necessary to examine the relationship between surface water and groundwater. El fenómeno descrito anteriormente se puede explicar más de la siguiente manera: reservorios de agua subterránea actúan para almacenar grandes cantidades de agua, que son transportados lentamente a elevaciones más bajas. La mayor parte de esta agua (alrededor del 98% a nivel mundial) es finalmente liberado de nuevo a las aguas superficiales. Con la filtración ser el proceso dominante, el flujo de las aguas subterráneas es lento y, por lo tanto, sujeto a una cantidad sustancial de difusión. El efecto neto es el de una contribución permanente de las aguas subterráneas a la superficie del agua en forma de flujo de base, o el flujo de estiaje de los ríos (Fig. 2-69). Para evaluar la variabilidad estacional de caudal, por lo tanto, es necesario examinar la relación entre el agua superficial y subterránea. Fig. 2-69  Large spring contributing to baseflow. / Gran primavera contribuir al caudal base. Annual Variability. Year-to-year streamflow variability shows some of the same features as those of seasonal streamflow variability. For instance, large catchments show runoff variability from one year to the next as a function of the state of moisture at the end of the first year and of the precipitation amounts added during the second year. As in the case of seasonal variability, annual streamflow variability is linked to the relative contributions of direct and indirect runoff. During dry years, precipitation goes on to replenish the catchment's soil moisture deficit, with little of it showing as direct runoff. This results in the low levels of runoff that characterize dry years. Conversely, during wet years, the catchment's moisture storage capacity fills up quickly, and any additional precipitation is almost entirely converted into surface runoff. This produces the high streamflow levels that characterize wet years. Annual streamflow variability is, therefore, intrinsically connected to the relative contributions of direct and indirect runoff. La variabilidad anual. Año a año la variabilidad del caudal muestra algunas de las mismas características que las de la variabilidad del caudal estacional. Por ejemplo, las grandes cuencas muestran escorrentía variabilidad de un año a otro en función del estado de la humedad al final del primer año y de las cantidades de precipitación añadidas durante el segundo año. Como en el caso de la variabilidad estacional, variabilidad anual caudal está vinculada a las contribuciones relativas de la escorrentía directa e indirecta. Durante los años de sequía, las precipitaciones se enciende para reponer el déficit de humedad del suelo de la cuenca, con poco de ella mostrando el escurrimiento directo. Esto da lugar a los bajos niveles de escorrentía que caracterizan años secos. Por el contrario, durante los años húmedos, la capacidad de almacenamiento de humedad de la cuenca se llena rápidamente, y cualquier precipitación adicional se convierte casi en su totalidad en la escorrentía superficial. Esto produce los niveles altos de caudal que caracterizan años húmedos. La variabilidad del caudal anual es, por lo tanto, intrínsecamente conectada a las contribuciones relativas de la escorrentía directa e indirecta. An increasingly popular line of inquiry is to focus on the mechanics of surface flow, interflow, and groundwater flow, while accounting for the spatial and temporal variability of the various physical, chemical, and biological processes involved at the various scales. However, the dearth of reliable data for all phases of the hydrologic cycle makes the evaluation of streamflow using a purely mechanistic approach a rather complex undertaking. Recent progress has been made in the coupling of mathematical models with geographic information systems, digital elevation models, and other related software. Una línea cada vez más popular de la investigación consiste en centrarse en la mecánica de flujo superficial, subsuperficial y flujo de agua subterránea, mientras que la contabilidad de la variabilidad espacial y temporal de las distintas propiedades físicas, químicas y procesos biológicos implicados en las distintas escalas. Sin embargo, la escasez de datos fiables para todas las fases del ciclo hidrológico hace que la evaluación de caudales utilizando un enfoque puramente mecanicista una tarea bastante compleja. Se han logrado avances recientes en el acoplamiento de modelos matemáticos con los sistemas de información geográfica, modelos digitales de elevación y otro software relacionado. A practical alternative which has enjoyed wide acceptance in applications of flood hydrology is the reliance on statistical tools to compensate for the incomplete knowledge of the physical processes. Over the years, this has given rise to the concept of flow frequency, or commonly, flood frequency, expressed as the average period of time (i.e., the return period) that it will take a certain flood level to recur at a given location. An annual flood series is abstracted from daily discharge measurements at a given gaging station. This is accomplished by either selecting the maximum daily flow for each of n years of record (the annual maxima series), or by selecting the n greatest flow values in the entire n-year record, regardless of when they occurred (the annual exceedance series) (Chapter 6). The statistical analysis of the flood series permits the calculation of the flow rates associated with one or more chosen frequencies. Una alternativa práctica que ha disfrutado de una amplia aceptación en las aplicaciones de la hidrología inundación es la dependencia de herramientas estadísticas para compensar el conocimiento incompleto de los procesos físicos. Con los años, esto ha dado lugar al concepto de frecuencia de flujo, o comúnmente, la frecuencia de inundaciones, expresada como el período medio de tiempo (es decir, el período de retorno) que tomará un cierto nivel de inundación que se repita en un lugar determinado. Una serie anual de inundaciones se abstrae de las mediciones diarias de descarga en una estación de aforo determinado. Esto se logra ya sea seleccionando el caudal máximo diario para cada uno de n años de registro (la serie anual maxima), o mediante la selección de las n mayores valores de flujo en todo el registro n-año, independientemente del momento en que se produjeron (la serie anual de excedencia ) (Capítulo 6). El análisis estadístico de la serie de inundación permite el cálculo de los caudales asociados a una o más frecuencias elegidas. The procedure is relatively straightforward, but it is limited by the record length. Its predictive capability decreases sharply when used to evaluate floods with return periods substantially in excess of the record length. An advantage of the method is its reproducibility, which means that two persons are likely to arrive at the same result when using the same methodology. This is a significant asset when comparing the relative merits of competing water resources projects. Methods for flood frequency analysis are discussed in Chapter 6. El procedimiento es relativamente sencillo, pero está limitada por la longitud de registro. Su capacidad predictiva disminuye drásticamente cuando se utiliza para evaluar las inundaciones con períodos de retorno sustancialmente superiores a la longitud del registro. Una ventaja del método es su reproducibilidad, lo que significa que dos personas son propensos a llegar al mismo resultado cuando se utiliza la misma metodología. Este es un activo importante al comparar los méritos relativos de competir proyectos de recursos hídricos. Métodos para el análisis de frecuencia de crecidas se discuten en el Capítulo 6. Recently, a complicating factor has arisen in flood frequency analysis. Global climate change promises to change the long-term depth-duration-frequency precipitation relations and, therefore, the magnitude and frequency of floods. Then, a historical flood record, however long, would have essentially lost its pristine character and could only serve as a rough indication for present and future analyses. Recientemente, un factor de complicación ha surgido en el análisis de frecuencia de crecidas. El cambio climático global promete cambiar los a largo plazo las relaciones de precipitaciones profundidad-duración-frecuencia y, por lo tanto, la magnitud y la frecuencia de las inundaciones. Entonces, un récord histórico de inundaciones, sin importar el tiempo, habría perdido esencialmente su carácter prístino y sólo podría servir como una indicación aproximada de análisis presente y futuro. Daily-flow Analysis. The variability of streamflow can also be expressed in terms of the day-to-day fluctuation of flow rates at a given station. Some streams show great variability from day to day, with high peaks and low valleys succeeding one another endlessly. Other streams show very little day-to-day variability, with high flows being not very different from low flows. Análisis diario de flujo. La variabilidad del caudal también se puede expresar en términos de la fluctuación del día a día de las tasas de flujo en una estación dada. Algunas corrientes muestran una gran variabilidad de día a día, con picos altos y valles bajos se suceden sin cesar. Otras corrientes muestran muy poca variabilidad día a día, con no ser muy diferente de flujos bajos flujos altos. The reason for this difference in behavior can be attributed to differences in the nature of catchment response. Small and midsize catchments are likely to have steep gradients and therefore to concentrate flows with negligible runoff diffusion, producing hydrographs that show a large number of high peaks and corresponding low valleys. Conversely, large catchments are likely to have milder gradients and therefore to concentrate flows with substantial runoff diffusion. The diffusion mechanism acts to spread the flows in time and space, resulting in a succession of smooth hydrographs showing low peaks and comparatively high valleys. La razón de esta diferencia de comportamiento se puede atribuir a las diferencias en la naturaleza de la respuesta de captación. Cuencas pequeñas y medianas empresas puedan tener pendientes pronunciadas y por lo tanto concentrar flujos con la difusión de escorrentía insignificante, produciendo hidrogramas que muestran un gran número de altas cumbres y los correspondientes valles bajos. Por el contrario, grandes zonas de captación es probable que tengan gradientes suaves y por lo tanto concentrar flujos de difusión sustancial con la escorrentía. El mecanismo de difusión actúa para difundir los flujos en tiempo y espacio, lo que resulta en una sucesión de hidrogramas lisas que muestran picos bajos y comparativamente altos valles. Daily flow data may not be sufficient to allow calculation of the runoff volumes produced by small watersheds. In cases where accuracy is required, hourly flows (or perhaps flows measured at 3-h intervals) may be necessary to describe adequately the temporal variability of the flow. Datos de flujo diarias pueden no ser suficientes para permitir el cálculo de los volúmenes de escorrentía producidas por pequeñas cuencas. En los casos donde se requiere precisión, los flujos por hora (o tal vez los flujos medidos a intervalos de 3 h) que sean necesarias para describir adecuadamente la variabilidad temporal del flujo. In the past four decades, the development of stochastic models of streamflow variability has resulted in a substantial body of knowledge referred to as stochastic hydrology. For a detailed treatment of this subject, see [8, 70, 89]. En las últimas cuatro décadas, el desarrollo de modelos estocásticos de la variabilidad del caudal se ha traducido en un importante cuerpo de conocimiento a que se refiere la hidrología como estocástico. Para un tratamiento detallado de este tema, ver [8, 70, 89]. Flow-duration Curve. A practical way to evaluate day-to-day streamflow variability is the flow-duration curve. To determine this curve for a particular location, it is necessary to obtain daily flow data for a certain period of time. either 1 y or a number of years. The length of the record indicates the total number of days in the series. The daily flow series is sequenced in decreasing order, from the highest to the lowest flow value. with each flow value being assigned an order number. For instance, the highest flow value would have order number one; the lowest flow value would have the last order number, equal to the total number of days. For each flow value, the percent time is defined as the ratio of its order number to the total number of days, expressed in percentage. The flow-duration curve is obtained by plotting flow versus percent time, with percent time in the abscissas and flow in the ordinates (Fig. 2-70). Flujo duración Curve. Una forma práctica de evaluar la variabilidad del caudal del día a día es la curva flujo-duración. Para determinar esta curva para una ubicación particular, es necesario obtener datos de flujo diarias durante un cierto período de tiempo. ya sea 1 y o un número de años. La longitud del registro indica el número total de días en la serie. La serie flujo diario se secuencia en orden decreciente, desde el más alto hasta el valor de caudal bajo. con cada valor de flujo que se le asigne un número de orden. Por ejemplo, el valor de flujo más alto tendría para el número uno; el valor de flujo más bajo tendría el último número de la orden, igual al número total de días. Para cada valor de flujo, el tiempo por ciento se define como la relación entre su número de pedido para el número total de días, expresado en porcentaje. La curva de flujo-duración se obtiene mediante el trazado de flujo en función del tiempo por ciento, con el tiempo por ciento en las abscisas y las ordenadas en el flujo (Fig. 2-70). Fig. 2-70  urva de duración de caudales. A flow-duration curve allows the evaluation of the permanence of characteristic low-flow levels. For instance, the flow expected to be exceeded 90 percent of the time can be readily determined from a flow-duration curve. The permanence of low flows is increased with streamflow regulation. The usual aim is to be able to assure the permanence of a certain low-flow level 100 percent of the time. Regulation causes a shift in the flow-duration curve by increasing the permanence of low flows while decreasing that of high flows (Fig. 2-67). Streamflow regulation is accomplished with storage reservoirs. Una curva flujo-duración permite la evaluación de la permanencia de los niveles de bajo flujo característicos. Por ejemplo, el flujo esperado que se exceda 90 por ciento del tiempo puede determinarse fácilmente a partir de una curva de flujo de duración. La permanencia de los caudales bajos se incrementa con la regulación de caudales. El objetivo habitual es ser capaz de asegurar la permanencia de un cierto nivel de bajo flujo 100 por ciento del tiempo. Reglamento provoca un desplazamiento en la curva de flujo duración mediante el aumento de la permanencia de los caudales bajos, mientras que la disminución de los caudales altos (Fig. 2-67). La regulación de caudales se logra con depósitos de almacenamiento. The flow-duration curve is helpful in the planning and design of water resources projects. In particular, for hydropower studies, the flow-duration curve serves to determine the potential for firm power generation. In the case of a run-of-the-river plant, with no storage facilities, the firm power is usually assumed on the basis of flow available 90 to 97 percent of the time. La curva flujo-duración es de gran ayuda en la planificación y diseño de proyectos de recursos hídricos. En particular, para los estudios de energía hidroeléctrica, la curva de flujo duración sirve para determinar el potencial para la generación de potencia firme. En el caso de una central de pasada el río, sin instalaciones de almacenamiento, la potencia firme se supone por lo general sobre la base del flujo disponible 90-97 por ciento del tiempo. Flow-mass Curve. Another way to evaluate day-to-day (and seasonal) streamflow variability is the flow-mass curve. A mass curve of daily values of a variable is a plot of time in the abscissas versus cumulative values of the variable in the ordinates. When using flow values, such a plot is referred to as the flow-mass curve. Masa de flujo de la curva. Otra forma de evaluar día a día (y de temporada) la variabilidad del caudal es la curva de masa de flujo. Una curva de masa de valores diarios de una variable es un gráfico de tiempo en las abscisas frente a los valores acumulados de la variable en las ordenadas. Cuando se utilizan valores de flujo, una parcela tal se conoce como la curva de flujo de masa. For daily flow records in cubic meters per second, the ordinates of the flow mass curve are in cubic meters or cubic hectometers (1 cubic hectometer = 1 million cubic meters). For any given day, the ordinate of the flow-mass curve is the accumulated runoff volume up to that day. According to Chow [10], the flow-mass curve is believed to have been first suggested by Rippl [69]; hence the name Rippl curve. The shape of the flow-mass curve resembles that of the letter S (Fig. 2-71); therefore, it is also referred to as the S-curve. Para los registros de caudal diario en metros cúbicos por segundo, las ordenadas de la curva de flujo de masa están en metros cúbicos o hectómetros cúbicos (1 hectómetro cúbico = 1 millón de metros cúbicos). Para un día cualquiera, la ordenada de la curva de flujo de masa es el volumen de escorrentía acumulada hasta ese día. Según Chow [10], se cree que la curva de flujo de masa que ha sido sugerido por primera vez por Rippl [69]; de ahí el nombre de la curva Rippl. La forma de la curva de flujo de masa se parece al de la letra S (Figura 2-71.); por lo tanto, también se refiere como la curva S. Applications of flow-mass curves are to reservoir design and operation, including the determination of reservoir capacity and the establishment of operating rules for storage reservoirs. Figure 2-70 shows a typical flow-mass curve. At any given time, the slope of the mass curve is a measure of the instantaneous flow rate. The slope of the line PQ, drawn between the points P and Q, represents the average flow between the two points. The slope of the line AB, drawn between the starting point A and the ending point B, is the average flow for the entire period. Aplicaciones de las curvas de masa de flujo son de diseño y operación de los embalses, incluyendo la determinación de la capacidad del depósito y el establecimiento de normas de funcionamiento para los depósitos de almacenamiento. La figura 2-70 muestra una curva de masa de flujo típico. En cualquier momento dado, la pendiente de la curva de la masa es una medida de la velocidad de flujo instantáneo. La pendiente de la línea PQ, trazada entre los puntos P y Q, representa el flujo medio entre los dos puntos. La pendiente de la línea AB, elaborado entre el punto A de inicio y el punto final B, es el flujo promedio para todo el periodo. Fig. 2-71  Una curva de masa. To use the flow-mass curve for reservoir design, two lines parallel to line AB and tangent to the flow-mass curve are drawn (Fig. 2-71). The first one, A'B', is tangent to the mass curve at the highest tangent point C. The second one, A"B", is tangent to the mass curve at the lowest tangent point D. The vertical difference between these two tangent lines, in cubic meters, is the storage volume required to release a constant flow rate. This constant release rate is equal to the slope of the line AB. A reservoir with a volume equal to AA" at the start would be full at C and empty at D, with no spill (excess volume) or shortage (deficit). A reservoir that is empty at the start has water while the S curve remains above the AB line and is empty (show a deficit) when the S curve moves below that line. A reservoir that is full at the start will spill water (excess volume) as long as the inflow remains greater than the outflow (from A to C). Para utilizar la curva de flujo de masa para el diseño del depósito, dos líneas paralelas a la línea AB y tangente a la curva de masa de flujo se dibujan (Fig. 2-71). La primera de ellas, A'B ', es tangente a la curva de la masa en el punto tangente más alto C. El segundo, una "B", es tangente a la curva de la masa en el punto tangente más bajo D. La diferencia vertical entre estos dos líneas tangentes, en metros cúbicos, es el volumen de almacenamiento requerido para liberar un caudal constante. Esta velocidad de liberación constante es igual a la pendiente de la línea AB. Un depósito con un volumen igual a AA "al comienzo sería completo en C y vacío en D, sin derrame (exceso de volumen) o la escasez (déficit). Un embalse que está vacía en el inicio tiene agua, mientras que los restos de la curva S por encima de la línea AB y está vacía (un déficit) cuando la curva S se mueve por debajo de esa línea. un embalse que está llena al inicio se derrame agua (exceso de volumen), siempre y cuando la entrada sigue siendo mayor que el de salida (de la A a C). The draft rate (or demand rate) is the release rate required to fulfill downstream needs, such as irrigation or power generation. A line having a slope equal to the draft rate is the draft line. The draft rate need not be necessarily constant. In practice, reservoir withdrawals are variable, leading to a variable draft rate and variable draft line, which amounts to an outflow mass curve. The superposition of inflow and outflow mass curves enables the detailed analysis of reservoir storage. El proyecto de tasa (o tasa de demanda) es la velocidad de liberación requerida para satisfacer las necesidades de aguas abajo, como el riego o generación de energía. Una línea tiene una pendiente igual a la velocidad de proyecto es el proyecto de la línea. El proyecto de la tasa no tiene que ser necesariamente constante. En la práctica, los retiros de depósito son variables, dando lugar a un proyecto de tipo de interés variable y el proyecto de línea de variable, lo que equivale a una curva de la masa de salida. La superposición de flujo de entrada y flujo de salida de masa curvas permite el análisis detallado de almacenamiento de depósito. The residual mass curve is a plot of the differences between the S curve ordinates and the corresponding ordinates from line AB. The ordinates of the residual mass curve can be either positive or negative. The residual mass curve accentuates the peaks and valleys of the cumulative flow record. La curva de masa residual es una gráfica de las diferencias entre las ordenadas de la curva S y las ordenadas correspondientes de la línea AB. Las ordenadas de la curva de la masa residual puede ser positivo o negativo. La curva de masa residual acentúa los picos y los valles del registro de flujo acumulativo. Range is the difference between the maximum and minimum ordinates of the residual mass curve for a given period. Range analysis was pioneered by Hurst [31, 32] who proposed the following formula for the calculation of maximum range: El rango es la diferencia entre las coordenadas máximos y mínimos de la curva de la masa residual durante un período determinado. Análisis Range fue iniciado por Hurst [31, 32], quien propuso la siguiente fórmula para el cálculo de alcance máximo:                   N R  =   s ( _____ ) 0.73                   2 (2-71) in which R = reservoir storage volume required to guarantee a constant release rate equal to the mean of the data (annual runoff volume) over a period of N years, and s = the standard deviation of the data (annual runoff volume) (Chapter 6) (Fig. 2-72). en el que el volumen de R = almacenamiento de depósito necesario para garantizar una velocidad constante de liberación igual a la media de los datos (volumen anual de escorrentía) durante un período de N años, y s = la desviación estándar de los datos (volumen anual de escorrentía) (Capítulo 6 ) (Fig. 2-72). Fig. 2-72  Lake Oroville, California. / Lago Oroville, California. Equation 2-71 was derived by curve-fitting data for a wide variety of natural phenomena. The exponent 0.73 was the mean of values varying between 0.46 and 0.96. A theoretical analysis based on the normal probability distribution (Chapter 6) showed that the exponent of Eq 2-71 should be 0.5 instead of 0.73. This apparent discrepancy between theory and data, known as the Hurst phenomenon, has been the subject of numerous studies [47]. Ecuación 2-71 se derivó por los datos de ajuste de curva para una amplia variedad de fenómenos naturales. El exponente 0,73 fue la media de los valores que varían entre 0,46 y 0,96. Un análisis teórico basado en la distribución de probabilidad normal (Capítulo 6) mostró que el exponente de la ecuación 2-71 debe ser 0,5 en lugar de 0,73. Esta aparente discrepancia entre la teoría y los datos, conocido como el fenómeno Hurst, ha sido el objeto de numerosos estudios [47]. Geographical Variability of Streamflow. Streamflow varies from one catchment to another and from one geographical region of a certain climate to another of a different climate. Moreover, exorheic and endorheic drainages have quite different streamflow patterns. While the outflow from an exorheic drainage is finite (nonzero), that of an endorheic drainage is zero, i.e., in the latter, no surface flow has a chance to leave the basin. Variabilidad geográfica de Tránsito. Caudal varía de una cuenca a otra y de una región geográfica de un cierto clima a otro de un clima diferente. Por otra parte, drenajes exorreicas y endorreicas tienen muy diferentes patrones de flujo fluvial. Mientras que el flujo de salida de drenaje exorreicos es finita (distinta de cero), la de drenaje endorheic es cero, es decir, en este último, no hay flujo de superficie tiene una oportunidad de salir de la cuenca. In exorheic drainages, the geographical variability of streamflow can be explained in terms of: En drenajes exorreicas, la variabilidad geográfica de caudal puede ser explicado en términos de: Catchment area, Área de influencia, Precipitation rates, amounts, seasonality, and climate, and El índice de precipitación, las cantidades, la estacionalidad, y el clima, y Temporal frame of reference. Marco temporal de referencia. Intuitively, the volume available for runoff is directly proportional to the catchment area. This, however, is tempered by the available precipitation, which is conditioned by the prevailing climate. The temporal frame refers to whether the streamflow evaluation is for short-term runoff (event, or storm, runoff) or long-term runoff (annual water yield). Intuitivamente, el volumen disponible para el escurrimiento es directamente proporcional a la zona de captación. Esto, sin embargo, se ve atenuada por la precipitación disponible, que está condicionada por el clima predominante. El marco temporal se refiere a si la evaluación de caudales es para el escurrimiento de corto plazo (evento, o una tormenta, la escorrentía) o el escurrimiento a largo plazo (rendimiento anual de agua). The catchment area is important in short-term evaluations, not only because of the potential runoff volume, but also because larger catchments tend to have milder overall gradients. (This is because the upper limit to catchment relief is in the thousands of meters, while the upper limit to catchment length is in the thousands of kilometers; a three order-of-magnitude difference). The generally milder gradients of large catchments lead to increased runoff diffusion, while enhancing the chances for infiltration and loss of surface water to groundwater. In flood hydrology applications, the net effect is a decrease in peak discharge per unit area. El área de influencia es importante en las evaluaciones a corto plazo, las cuencas no sólo por el volumen potencial de escurrimiento, sino también porque más grandes tienden a tener gradientes en general leves. (Esto se debe a que el límite superior para el alivio de captación está en los miles de metros, mientras que el límite superior a la longitud de captación está en los miles de kilómetros; una diferencia de tres orden de magnitud). Los gradientes generalmente más leves de grandes cuencas conducen a una mayor difusión de la escorrentía, al tiempo que mejora las posibilidades de infiltración y la pérdida de agua superficial al agua subterránea. En las aplicaciones de la hidrología de las inundaciones, el efecto neto es una disminución de caudal máximo por unidad de área. The above reasoning is supported by data showing peak flows to be directly related to catchment area, as shown in Eq. 2-49. Consequently, the peak discharge per unit area is: El razonamiento anterior es apoyado por datos que mostraron que los flujos máximos estar directamente relacionado con la zona de influencia, como se muestra en la ecuación. 2-49. En consecuencia, el caudal máximo por unidad de área es:              c qp  =  _____             Am (2-72) in which qp = peak discharge per unit area, in m3 s-1 km-2 (or alternatively, in ft3 s-1 mi-2); A = catchment area, in km2 (or mi2), and c and m are empirical constants, with m = 1 - n. Since n is generally less than 1, it follows that m is also generally less than 1. Equation 2-72 confirms that peak discharge per unit area is inversely related to drainage area. An example of such a trend is given by the classical Creager curves, shown in Fig. 2-73 [14]: en el que qp = caudal máximo por unidad de área, en m3 s-1 KM-2 (o, alternativamente, en m3 s-1 mi-2); A = área de captación, en km2 (o MI2), y c y m son constantes empíricas, con m = 1 - n. Dado que n es generalmente menor que 1, se deduce que m también es generalmente inferior a 1. Ecuación 2-72 confirma que el pico de descarga por unidad de área está inversamente relacionada con el área de drenaje. Un ejemplo de esta tendencia está dada por las curvas clásicas Creager, mostrados en la Fig. 2-73 [14]: qp  =  46 C A ( 0.894 A - 0.048  -  1 ) (2-73) Values of C in the range 30-100 encompass most of the flood data compiled by Creager et al. [14]. This range can be taken as a measure of the regional variability of flood discharges. Equation 2-73, however, limits itself to providing a peak discharge per unit area, wIth no connotation of frequency attached to the calculated values. Los valores de C en el rango de 30 a 100 abarcan la mayor parte de los datos recopilados por las inundaciones Creager et al. [14]. Este rango puede ser tomado como una medida de la variabilidad regional de los vertidos de inundación. Ecuación 2-73, sin embargo, se limita a proporcionar un caudal máximo por unidad de superficie, sin connotación de frecuencia unida a los valores calculados. Fig. 2-73  Creager curves:  Curvas de Creager: descarga de inundación por unidad de área vs área de drenaje (Haga clic -aquí- para desplegar). For short-term (event or storm) runoff evaluations, the precipitation rate and catchment abstractive capability determine the streamflow variability. In small catchments, runoff is characterized by the event runoff coefficient C, i.e., the ratio of storm runoff depth to storm rainfall depth (Chapter 4). This ratio increases with the impermeability of the catchment surface, from values close to zero (0.10 ≤ C ≤ 015) for highly permeable surfaces, to values close to one (0.80 ≤ C ≤ 0.95) for highly impermeable surfaces. This underscores the role of infiltration as the leading abstracting mechanism in the short term (storm event). Para corto plazo (evento o tormenta) evaluaciones de escorrentía, la tasa de precipitación y de captación capacidad abstractiva determinar la variabilidad de caudales. En las pequeñas cuencas, la escorrentía se caracteriza por el coeficiente de escorrentía evento C, es decir, la relación de la tormenta profundidad escorrentía de tormenta profundidad precipitaciones (capítulo 4). Esta relación aumenta con la impermeabilidad de la superficie de captación, desde valores cercanos a cero (0,10 d C d 015) para superficies altamente permeables, a valores cercanos a uno (0,80 d C d 0,95) para superficies altamente impermeables. Esto pone de relieve el papel de la infiltración como el mecanismo de abstracción que lleva en el corto plazo (evento de tormenta). For long-term (water yield) runoff evaluations, geographical location and associated climate determine to a large extent the seasonal and annual variability of streamflow. In the typical exorheic drainage, mean annual runoff increases with environmental moisture, i.e., the moisture present in soil and air. The mean annual runoff coefficient K, i.e., the ratio of mean annual runoff to mean annual rainfall, varies from 0.02 ≤ K ≤ 0.15 in arid and semiarid regions, to 0.5 ≤ K ≤ 0.7 in humid and extremely humid regions. Thus, in arid and semiarid regions, a larger fraction of total precipitation (0.85-0.98) is returned to the atmosphere, mostly via evaporation from soil and bare ground. Conversely, in humid and extremely humid regions, a smaller fraction of total precipitation (0.3-0.5) is returned to the atmosphere, primarily through evaporation from water bodies and evapotranspiration from vegetation. This depicts the importance of evaporation and evapotranspiration as the leading abstractive mechanisms in the long term (water yield). Para largo plazo (producción de agua) las evaluaciones de escorrentía, la ubicación geográfica y el clima asociado determinará en gran medida la variabilidad estacional y anual de caudales. En el drenaje típica exorreicos, significará un aumento anual de escorrentía con la humedad ambiental, es decir, la humedad presente en el suelo y el aire. La media anual de coeficiente de escorrentía K, es decir, la relación de la escorrentía media anual de precipitación media anual, varía de 0,02 d K d 0,15 en las regiones áridas y semiáridas, a 0,5 d K d 0,7 en las regiones húmedas y muy húmedas. Por lo tanto, en las regiones áridas y semiáridas, una mayor fracción de la precipitación total (0,85 hasta 0,98) se devuelve a la atmósfera, sobre todo a través de la evaporación del suelo y el suelo desnudo. Por el contrario, en las regiones húmedas y muy húmedas, una fracción más pequeña de la precipitación total (0,3-0,5) se devuelve a la atmósfera, principalmente a través de la evaporación de los cuerpos de agua y la evapotranspiración de la vegetación. Esto representa la importancia de la evaporación y la evapotranspiración como los mecanismos abstractivos líderes en el largo plazo (producción de agua). PREGUNTAS [Problemas]   [Bibliografía]   •   [Arriba]   [Precipitación]   [Abstracciones Hidrológicas]   [Características de la Cuenca]   [Escurrimiento]   Describe the frontal lifting of air masses. Describa el levantamiento frontal de masas de aire. What is orographic lifting? What is thermal lifting? ¿Qué es la elevación orográfica? ¿Qué es la elevación térmica? Describe the concept of rainfall frequency. Describa el concepto de frecuencia de precipitaciones. What is the PMP? What is the PMF? ¿qué es la PMP? ¿Qué es el PMF? In what case is the isohyetal method preferred over the Thiessen polygons method? ¿En qué instancia se prefiere el método de isoyetas sobre el método de polígonos Thiessen? When is an IDF curve used? When is a Depth-Duration-Frequency value used? Cuando se utiliza una curva IDF? Cuando se utiliza un valor de profundidad-Duración-Frecuencia? How does average annual precipitation affect climate? ¿Cómo afecta la precipitación media anual al clima? When is the normal ratio method used to fill in missing precipitation records? ¿Cuándo se utiliza el método de taza normal para suplir la falta de registros de precipitación? What is a double-mass analysis? ¿Qué es un análisis de masa doble? What type of storm is likely to be subtantially abstracted by interception? ¿Qué tipo de tormenta tiene tendencia a ser abstraída sustancialmente mediante la interceptación? What factors affect the process of infiltration? ¿Qué factores afectan el proceso de infiltración? Compare the Horton and Philip infiltration formulas. Compare las fórmulas de infiltración de Horton y Philip. What type of application justifies the use of a φ-index? ¿Qué tipo de aplicación justifica el uso de un índice φ? In what case is depression storage likely to be important in runoff evaluation? ¿En qué caso puede ser importante la depresión de almacenamiento en la evaluación de la escorrentía? What is the basis of the energy budget method for determining reservoir evaporation? ¿Cuál es la base del método de balance de energía en la determinación la evaporación de un depósito? What is albedo? What is the albedo of a forest? Of a desert? ¿Qué es el albedo? ¿Cuál es el albedo de un bosque? De un desierto? What assumptions did Penman use in deriving his evaporation formula? ¿Qué suposiciones hizo Penman al derivar su fórmula de evaporación? What is transpiration? Why is it considered a hydrologic abstraction? ¿Qué es la transpiración? ¿Por qué se considera una abstracción hidrológica? What is potential evapotranspiration? What is actual evapotranspiration? ¿Qué es evapotranspiración potencial? ¿Qué es evapotranspiración real? What is reference crop evapotranspiration? ¿Qué es evapotranspiración de cultivo de referencia? What is the rationale for using evaporation formulas in the evaluation of evapotranspiration? ¿Cuál es la justificación del uso de fórmulas de evaporación en la evaluación de la evapotranspiración? What are the various types of surface flow that can occur in nature? ¿Cuáles son los distintos tipos de flujo superficial que pueden ocurrir en la naturaleza? What is a hypsometric curve? When is it used? ¿Qué es una curva hipsométrica? Cuando se utiliza? Derive the formula for equivalent slope (Eq. 2-52). State any assumptions used. Derive la fórmula para la pendiente equivalente (Ec. 2-52). Indique cualquier supuesto utilizado. What is interflow? What is groundwater flow? ¿Qué es interflujo? ¿Qué es flujo de agua subterránea? What is direct runoff? What is indirect runoff? ¿Cuál es la escorrentía directa? ¿Cuál es la escorrentía indirecta? How does an ephemeral stream differ from an intermittent stream? ¿Cómo difieren la corriente efímera y la corriente intermitente? Why is the catchment's antecedent moisture important in flood hydrology? ¿Por qué es importante la humedad antecedente de la cuenca en la hidrología de inundaciones? What is catchment response? What is runoff concentration? What is runoff diffusion? ¿Qué es la respuesta de captación? ¿Que es la concentración de la escorrentía? ¿Qué es la difusión de escorrentía? Why do single-storm streamflow hydrographs generally exhibit a long tail? ¿Por qué los hidrogramas de caudal de una sola tormenta generalmente exhiben una cola larga? Why is the Manning equation preferred over the Chezy equation in practice? ¿Por qué en la práctica se prefiere la ecuación de Manning sobre la ecuación Chezy? What is the advantage of the Chezy equation? ¿Cuál es la ventaja de la ecuación Chezy? Discuss low flows and high flows in connection with arid and humid climates. Discuta flujos bajos y altos flujos en relación con los climas áridos y húmedos. What is a rating curve? What are the various processes likely to affect a rating? ¿Qué es una curva de gastos? ¿Cuáles son los diferentes procesos que pueden afectar a una curva de gastos? How can seasonal and annual streamflow variability be explained? ¿Cómo se puede explicar la variabilidad estacional y anual de caudales? What is the reason for the high peaks and low valleys of typical daily streamflows of small upland catchments? ¿Cuál es la razón de las altas cumbres y valles bajos de los caudales diarios típicos de las pequeñas cuencas de montaña? What is a flow-duration curve? For what is it used? ¿Qué es una curva de flujo-duración? ¿Para qué se utiliza? What is a flow-mass curve? For what is it used? ¿Qué es una curva de flujo-masa? ¿Para qué se utiliza? What is the Hurst phenomenon? ¿Qué es el fenómeno Hurst? How does peak discharge per unit area vary with catchment size? Why? ¿Cómo varía la descarga máxima por unidad de superficie de acuerdo al tamaño de la cuenca? ¿Por qué? PROBLEMAS [Bibliografía]   •   [Arriba]   [Precipitación]   [Abstracciones Hidrológicas]   [Características de la Cuenca]   [Escurrimiento]   [Preguntas]   A 465-km2 catchment has mean annual precipitation of 775 mm and mean annual flow of 3.8 m3/s. What percentage of total precipitation is abstracted by the catchment? Una cuenca de 465 km2 tiene una precipitación media anual de 775 mm y un flujo medio anual de 3.8 m3/s. ¿Qué porcentaje de la precipitación total se abstrae por la cuenca? A 9250-km2 catchment has mean annual precipitation of 645 mm and mean annual flow of 37.3 m3/s. What is the precipitation depth abstracted by the catchment? Una cuenca de 9,250 km2 con precipitación media anual de 645 mm y flujo medio anual de 37.3 m3/s. ¿Cuál es la profundidad de la precipitación abstraída por la cuenca? Using the dimensionless temporal rainfall distribution shown in Fig. 2-5, calculate a hyetograph for an 18-cm, 12-h storm, defined at l-h intervals. Usando la distribución de precipitaciones temporal adimensional que se muestra en la Fig. 2-5, calcule un pluviograma para una tormenta de 18 cm y 12-h, definida en intervalos de 1-hora. A 100-km2 catchment is instrumented with 13 rain gages located as shown in Fig. P-2-4. Immediately after a certain precipitation event, the rainfall amounts accumulated in each gage are as shown in the figure. Calculate the average precipitation over the catchment by the following methods: (a) average rainfall, (b) Thiessen polygons, and (c) isohyetal method. Una cuenca de 100 km2 está equipada con 13 pluviómetros situados como se muestra en la Fig. P-2-4. Inmediatamente después de un determinado evento de precipitación, las cantidades de lluvia acumuladas en cada instrumento son como se muestra en la figura. Calcular la precipitación media de la cuenca por medio de los siguientes métodos: (a) la precipitación media, (b) los polígonos de Thiessen, y (c) el método de isoyetas. 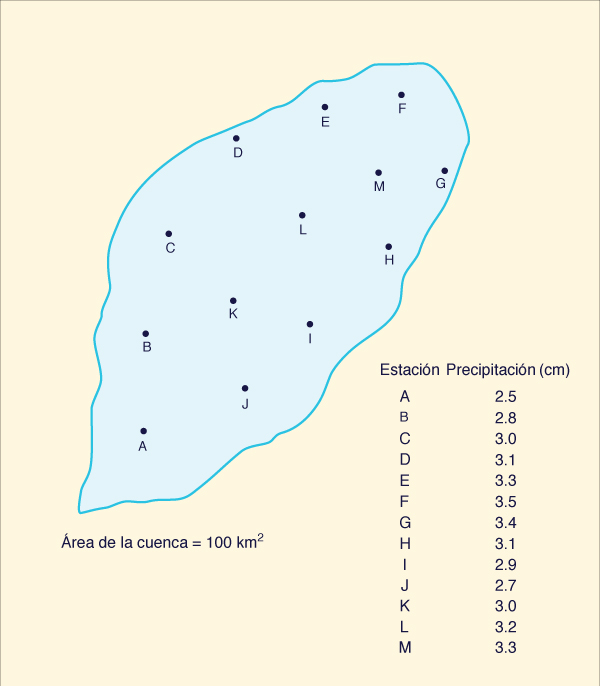Fig. P-2-4  Fig. Distribución espacial de pluviómetros para Problema 2-4. A certain catchment experienced a rainfall event with the following incremental depths: Una cuenca determinada experimentó un evento de precipitación con las siguientes profundidades incrementales: Time (h) / Tiempo (h) 0-3 3-6 6-9 9-12 Rainfall (cm) / Precipitación (cm) 0.4 0.8 1.6 0.2 Determine: (a) the average rainfall intensity in the first 6 h, (b) the average rainfall intensity for the entire duration of the storm. Determine: (a) la intensidad media de lluvia en las primeras 6 h, (b) la intensidad media de lluvia para la duración completa de la tormenta. The following dimensionless temporal rainfall distribution has been determined for a local storm: La siguiente distribución temporal adimensional de precipitaciones se ha determinado para una tormenta local: Time (%) / Tiempo (%) 0 10 20 30 40 50 60 70 80 90 100 Rainfall depth (%) / Profundidad de precipitación (%) 0 5 10 25 50 75 90 95 97 99 100 Calculate a design hyetograph for a 12-cm, 6-h storm. Express in terms of hourly rainfall depths. Calcule un pluviometro de diseño para una tormenta de 12 cm y 6-horas. Exprese en términos de profundidad de lluvia por hora. Given the following intensity-duration data, find the a and m constants of Eq. 2-5. Calcule las constantes a y m de la Ec. 2-5, de acuerdo a los siguientes datos de intensidad-duración. Intensity (mm/h) / Intensidad (mm/h) 50 30 Duration (h) / Duración (h) 0.5 1.0 Given the following intensity-duration data, find the constants a and b of Eq. 2-6. Dados los siguientes datos de intensidad-duración, encontrar las constantes a y b de la ecuación. 2-6. Intensity (mm/h) / Intensidad (mm/h) 60 40 Duration (h) / Duración (h) 1 2 Construct a depth-area curve for the 6-h duration isohyetal map shown in Fig. P-2-9. Construya una curva de profundidad-área para el mapa de isoyetas de 6 horas de duración que se muestra en la Fig. P-2-9. 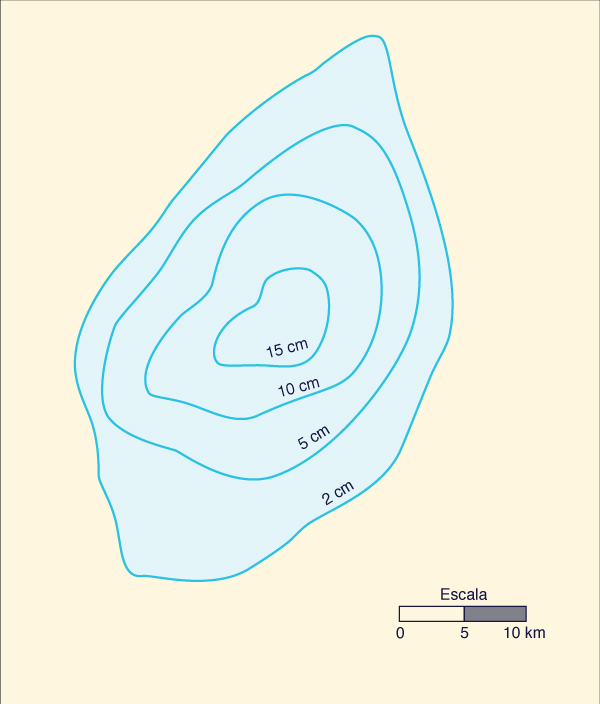Fig. P-2-9  Mapa de isoyetas para el problema 2-9. The precipitation gage for station X was inoperative during part of the month of January. During that same period, the precipitation depths measured at three index stations A, B, and C were 25, 28, and 27 mm, respectively. Estimate the missing precipitation data at X. given the following average annual precipitation at X, A, B, and C: 285, 250, 225, and 275 mm, respectively. El medidor de precipitación estuvo fuera de servicio durante parte del mes de enero. Durante ese mismo período, las profundidades de precipitaciones medidas en tres estaciones de índice A, B, y C fueron 25, 28 y 27 mm, respectivamente. Estime los datos de precipitación que faltantes en X. La precipitación media anual en X, A, B, y C fue: 285, 250, 225 y 275 mm, respectivamente. The precipitation gage for station Y was inoperative during a few days in February. During that same period, the precipitation at four index stations, each located in one of four quadrants (Fig. 2-15), is the following: El medidor de precipitación de la estación Y estuvo fuera de servicio durante varios días en febrero. (Fig. 2-15) Durante ese mismo período, la precipitación en cuatro estaciones de índice, cada uno situado en uno de los cuatro cuadrantes, es la siguiente: Quadrant) / Cuadrante Precipitation / Precipitación (mm) Distance / Distancia (km) I 25 8.5 II 28 6.2 III 27 3.7 IV 30 15.0 Estimate the missing precipitation data at station Y. Estime los datos de precipitación que faltan en la estación Y. The annual precipitation at station Z and the average annual precipitation at 10 neighboring stations are as follows: La precipitación anual en la estación Z y la precipitación media anual en 10 estaciones cercanas se muestra a continuación: Year / Año Precipitation at Z (mm) / Precipitación en Z (mm) 10-station average (mm) / Promedio de 10 estaciones (mm) 1972 35 28 1973 37 29 1974 39 31 1975 35 27 1976 30 25 1978 25 21 1979 20 17 1980 24 21 Year / Año Precipitation at Z (mm) / Precipitación en Z (mm) 10-station average / Promedio de 10 estaciones (mm) (mm) 1981 30 26 1982 31 31 1983 35 36 1984 38 39 1985 40 44 1984 28 32 1985 25 30 1985 21 23 Use double-mass analysis to correct for any data inconsistencies at station Z. Utilice el análisis de masa doble para corregir las inconsistencias de datos en la estación Z. Calculate the interception loss for a storm lasting 30 min, with interception storage 0.3 mm, ratio of evaporating foliage surface to its horizontal projection K = 1.3, and evaporation rate E = 0.4 mm/h. Calcular la pérdida por intercepción para una tormenta que dura 30 min, con almacenamiento de intercepción de 0.3 mm, la proporción de superficie de evaporación de follaje a proyección horizontal es K = 1.3, y velocidad de evaporación E = 0.4 mm/h. Show that F = (fo - fc)/k, in which F is the total infiltration depth above the f = fc line, Eq. 2-13. Demuestre que F = (fo - fc)/k, en la cual F es la profundidad total de infiltración por encima de la línea de f = fc, Ec. 2-13. Fit a Horton infiltration formula to the following measurements: Use las siguientes medidas para derivar una fórmula de infiltración de Horton: Time (h) / Tiempo (h) f (mm/h) 1 2.35 3 1.27 ∞ 1.00 Given the following measurements, determine the parameters of the Philip infiltration equation. Dadas las siguientes mediciones, determinar los parámetros de la ecuación de infiltración de Philip. Time (h) / Tiempo (h) f (mm/h) 2 1.7 4 1.5 The following rainfall distribution was measured during a 12-h storm: La siguiente distribución de precipitaciones se midió durante una tormenta de 12 horas: Time (h) / Tiempo (h) 0-2 2-4 4-6 6-8 8-10 10-12 Rainfall intensity (cm/h) / Intensidad de la lluvia (cm / h) 1.0 2.0 4.0 3.0 0.5 1.5 Runoff depth was 16 cm. Calculate the φ-index for this storm. La escorrentía de profundidad fue de 16 cm. Calcule el-índice φ para esta tormenta. Using the data of Problem 2-17, calculate the W-index, assuming the sum of interception loss and depth of surface storage is S = 1 cm. Utilizando los datos del problema 2-17 calcule el índice W, suponiendo que la suma de la pérdida de intercepción y la profundidad de almacenamiento en superficie es S = 1 cm. A certain catchment has a depression storage capacity of Sd = 2 mm. Calculate the equivalent depth of depression storage for the following values of precipitation excess: (a) 1 mm, (b) 5 mm, and (c) 20 mm. Una cuenca determinda tiene una capacidad de almacenamiento en la depresión de Sd = 2 mm. Calcule la profundidad equivalente de almacenamiento en la depresión para los siguientes valores de exceso de precipitación: (a) 1 mm, (b) 5 mm, y (c) 20 mm. Use the Meyer equation to calculate monthly evaporation for a large lake, given the following data: month of July, mean monthly air temperature 70°F, mean monthly relative humidity 60%, monthly mean wind speed at 25-ft height, 20 mi/h. Utilice la ecuación de Meyer para calcular la evaporación mensual de un lago extenso, dados los siguientes datos: para el mes de julio, la temperatura media mensual del aire es 70°C, humedad relativa media mensual de 60%, la velocidad del viento media mensual en la altura de 25 pies igual a 20 millas/h. Derive the Penman equation (Eq. 2-36). Derive la Ecuación de Penman (Ec. 2-36). Use the Penman method to calculate the evaporation rate for the following atmospheric conditions: air temperature, 25°C; net radiation, 578 cal/cm2/d, wind speed at 2-m above the surface, v2 = 150 km/d; relative humidity, 50%. Utilice el método de Penman para calcular la velocidad de evaporación para las siguientes condiciones atmosféricas: temperatura del aire = 25°C; radiación neta = 578 cal/ cm2/día: la velocidad del viento a 2 m por encima de la superficie, v2 = 150 km/d; humedad relativa = 50%. Use the Penman method (together with the Meyer equation) to calculate the evaporation rate (in inches per day) for the following atmospheric conditions: air temperature, 70°F, water surface temperature, 50°F, daily mean wind speed at 25-ft height, W = 15 mi/h, relative humidity 30%, net radiation, Qn = 15 Btu/ in.2/ d. Assume a large lake to use Eq. 2-27 (b). Utilice el método de Penman (junto con la ecuación de Meyer) para calcular la tasa de evaporación (en pulgadas por día) para las siguientes condiciones atmosféricas: temperatura del aire = 70°C, temperatura de la superficie del agua = 50°C, velocidad del viento media diaria a 25 pies de altura, W = 15 millas/h; humedad relativa de 30%, radiación neta, Qn = 15 Btu/pulg2/d. Asuma un lago extenso y utilice la Ec. 2-27 (b). Use the Blaney-Criddle method (with corrections due to Doorenbos and Pruitt) to calculate reference crop evapotranspiration during the month of July for a geographic location at 40°N, with mean daily temperature of 25°C. Assume high actual insolation time, 70% minimum relative humidity, and 1 m/s daytime wind speed. Utilice el método de Blaney-Criddle (con las correcciones de Doorenbos y Pruitt) para calcular la evapotranspiración del cultivo de referencia durante el mes de julio para una ubicación geográfica situadaa 40°N, con una temperatura media diaria de 25°C. Asumir una hora de insolación real alta, una humedad relativa mínima de 70%, y velocidad del viento durante el día de 1m/s. Use the Thornthwaite method to calculate the potential evapotranspiration during the month of May for a geographic location at 35°N, with the following mean monthly temperatures, in degrees Celsius. Utilice el método Thornthwaite para calcular la evapotranspiración potencial durante el mes de mayo para una ubicación geográfica situada a 35°N, con las siguientes temperaturas medias mensuales, en grados Celsius. Ene Feb Mar Abr May Jun Jul Ago Sep Oct Nov Dic 6 8 10 12 15 20 25 20 16 12 10 8 Use the Priestley and Taylor formula to calculate the potential evapotranspiration for a site with air temperature of 15°C and net radiation of 560 cal/cm2/d. Use la fórmula de Priestley y Taylor para calcular la evapotranspiración potencial en un sitio con temperatura de aire de 15°C y radiación neta de 560 cal/cm2/d. The following data have been obtained by planimetering a 135-km2 catchment: Los siguientes datos se han obtenido por planimetría para una cuenca de 135 km2: Elevation (m) / Elevación (m) Subarea above indicated elevation (km2) / Subárea anterior elevación indicada (km2) 1010 135 1020 85 1030 65 1040 30 1050 12 1060 4 1070 0 Calculate a hypsometric curve for this catchment. Calcule una curva hipsométrica para la cuenca. Derive the formula for the compactness ratio Kc (Eq. 2-51). Derive la fórmula para la relación de compacidad Kc (Ec. 2-51). Given the following longitudinal profile of a river channel, calculate the following slopes: (a) S1, (b) S2, and (c) S3. Dado el perfil longitudinal siguiente de un canal de río, calcular los siguientes pistas: (a) S1, (b) S2, y (c) S3. Distance (km) / Distancia (km) 0 50 100 150 200 250 300 Elevation (m) 10 30 60 100 150 220 350 The bottom of a certain 100-km reach of a river can be described by the following longitudinal profile: La parte inferior de un cierto 100-km alcance de un río puede ser descrita por el siguiente perfil longitudinal: y = 100 e -0.00001 x in which y = elevation with reference to an arbitrary datum, in meters; and x = horizontal distance measured from upstream end of the reach, in meters. Calculate the S2 slope. en la que y = elevación con referencia a un dato arbitrario, en metros; y x = distancia horizontal medida a partir de extremo aguas arriba del alcance, en metros. Calcular la pendiente S2. Given the following 14-d record of daily precipitation, calculate the antecedent precipitation index API. Assume the starting value of the index to be equal to 0 and the recession constant K = 0.85. Dada la siguiente ficha 14-d de precipitación diaria, calcule el antecedente API índice de precipitación. Suponga que el valor inicial del índice sea igual a 0 y la constante K recesión = 0,85. Day / Día Precipitation (cm) / Precipitación (cm) 1 0.0 2 0.1 3 0.3 4 0.4 5 0.2 Day / Día Precipitation (cm) /Precipitación (cm) 6 0.0 7 0.0 8 0.7 9 0.8 10 0.9 Day / Día Precipitation (cm) / Precipitación (cm) 11 1.2 12 0.5 13 0.0 14 0.0     A 35-ha catchment experiences 5 cm of precipitation, uniformly distributed in 2 h. If the time of concentration is 1 h, what is the maximum possible flow rate at the catchment outlet? A 35-ha experiencias de captación de 5 cm de precipitaciones, uniformemente distribuidos en 2 h. Si el tiempo de concentración es de 1 h, ¿cuál es el caudal máximo posible en la salida de la cuenca? Calculate hourly ordinates of a gamma hydrograph with the following characteristics: peak flow, 1000 m3/s; baseflow, 0 m3/s; time-to-peak, 3 h; and time-to-centroid, 6 h. Calcula ordenadas por hora de un hidrograma gamma con las siguientes características: el flujo máximo, 1.000 m3 / s; caudal base, 0 m3 / s; tiempo hasta el pico, 3 h; y tiempo de salida al centroide, 6 h. The following data have been measured in a river: mean velocity V = 1.8 m/s, hydraulic radius R = 3.2 m, channel slope S = 0.0005. Calculate the Manning and Chezy coefficients. Los siguientes datos se han medido en un río: velocidad media V = 1,8 m / s, el radio R hidráulica = 3,2 m, pendiente del canal S = 0.0005. Calcular los coeficientes de Manning y Chezy. The Chezy coefficient for a wide channel is C = 49 m1/2/s and the bottom slope is S = 0.00037. What is the Froude number of the uniform (i.e., steady equilibrium) flow? El coeficiente Chezy para un canal de ancho es C = 49 m1 / 2 / s, y la pendiente del fondo es S = 0,00037. ¿Cuál es el número de Froude del uniforme (es decir, el equilibrio estable) fluya? The flow duration characteristics of a certain stream can be expressed as follows: Las características de duración de flujo de una determinada corriente se pueden expresar como sigue: Q = ( 950 /T )  +  10 in which Q = discharge in cubic meters per second, and T = percent time, restricted to the range 1-100%. What flow can be expected to be exceeded: (a) 90% of the time, (b) 95% of the time, and (c) 100% of the time? en la que Q = descarga en metros cúbicos por segundo, y el tiempo T = ciento, restringido a la gama de 1-100%. Lo flujo se puede esperar que se supere: (a) 90% del tiempo, (b) 95% del tiempo, y (c) 100% del tiempo? A reservoir has the following average monthly inflows, in cubic hectometers (million of cubic meters): Un depósito tiene las siguientes entradas mensuales promedio, en hectómetros cúbicos (millones de metros cúbicos): Jan / Ene Feb Mar Apr / Abr May Jun Jul Aug / Ago Sep Oct Nov Dec / Dic 30 34 35 48 72 85 72 55 51 40 34 32 Determine the reservoir storage volume required to release a constant draft rate throughout the year. Determinar el volumen de almacenamiento del depósito necesario para lanzar un proyecto de tasa constante durante todo el año. The analysis of 43 y of runoff data at a reservoir site in a large river has led to the following: mean annual runoff volume, 24 km3; standard deviation, 7 km3. What is the reservoir storage volume required to guarantee a constant release rate equal to the mean of the data? El análisis de los 43 y de los datos de escorrentía en un sitio de depósito en un gran río ha dado lugar a lo siguiente: volumen medio anual de escurrimiento, 24 km3; desviación estándar, 7 km3. ¿Cuál es el volumen de almacenamiento del depósito necesario para garantizar una velocidad de liberación constante igual a la media de los datos? Calculate the peak discharge for a 1,000-mi2 drainage area using the Creager formula (Eq. 2-73) with (a) C = 30, and (b) C = 100. Calcular el caudal máximo para un área de drenaje de 1.000 km2 utilizando la fórmula Creager (Ec. 2-73) con (a) C = 30, y (b) C = 100. BIBLIOGRAFÍA •   [Arriba]   [Precipitación]   [Abstracciones Hidrológicas]   [Características de la Cuenca]   [Escurrimiento]   [Preguntas]   [Problemas]   American Society of Civil Engineers. (1949). "Hydrology Handbook," Manual of Engineering Practice No. 28. American Society of Civil Engineers. (1960). "Design and Construction of Sanitary Storm Sewers," Manual of Engineering Practice No. 37. American Society of Civil Engineers. (1990). "Evapotranspiration and Irrigation Water Requirements," Manual of Engineering Practice No. 70. Barnes, H. H., Jr. (1967). "Roughness Characteristics of Natural Channels," U.S. Geological Survey Water Supply Paper No. 1849. Blaney, H. F., and W. D. Criddle. (1950). "Determining Water Requirements in Irrigated Areas from Climatological and Irrigation Data," USDA Irrigation and Water Conservation, SCS TP-96. August. Blaney, H. F., and W. D. Criddle. (1962). "Determining Consumptive Use of Irrigation Water Requirements," USDA Technical Bulletin No. 1275, Washington, D.C. Bowen, I. S. (1926). "The Ratio of Heat Losses by Conduction and by Evaporation from any Water Surface," Physics Review, Vol. 27, pp. 779-787. Bras, R., and I. Rodriguez-Iturbe. (1985). Random Functions and Hydrology. Reading, Mass.: Addison-Wesley. Bruce, J. P., and G. K. Rodgers. (1962). "Water Balance in the Great Lakes System, Great Lakes Basin," American Association for the Advancement of Science, Publication No. 71, Washington, D.C. Bruce, J. P. , and R. H. Clark. (1966). Introduction to Hydrometeorology. Elmsford, NY: Pergamon Press. Bull, W. B. (1991). Geomorphic Response to Climatic Change. Oxford University Press, New York. Chow, V. T. (1964). Handbook of Applied Hydrology. New York: McGraw-Hili. Cook, H. L. (1946). "The Infiltration Approach to the Calculation of Surface Runoff," Transactions, American Geophysical Union, Vol. 27, No. V, October, pp. 726-747. Creager, W. P., J. D. Justin, and J. Hinds. (1945). Engineering for Dams. Vol. 1, General Design. New York: John Wiley. Dalton, J. (1802). "Experimental Essays on the Constitution of Mixed Gases; on the Force of Steam or Vapor from Water and Other Liquids, Both in a Torricellian Vacuum and in Air; on Evaporation; and on the Expansion of Gases by Heat," Manchester Literary and Philosophical Society Proceedings, Vol. 5, pp. 536-602. Doorenbos J., and W. O. Pruitt. (1977). "Guidelines for Predicting Crop Water Requirements," Irrigation and Drainage Paper No. 24, FAO, Rome. Dunne, T., and L. B. Leopold. (1978). Water in Environmental Planning. San Francisco: Freeman and Co. Environmental Data Service, Environmental Science Services Administration, U.S. Department of Commerce, "Climatic Atlas of the United States," 1968. Fread, D. L. (1985). "Channel Routing," in Hydrological Forecasting, M. G. Anderson and T. P. Burt, eds. New York: John Wiley. Frevert, D. K., R. W. Hill, and B. C. Braten. (1983). "Estimation of FAO Evapotranspiration Coefficients," J. Irrigation Drainage Engrg., ASCE, Vol. 109, No. IR2, pp. 265-270. Green, W. H. and G. A. Ampt. (1911). "Studies on Soil Physics. 1. The Flow of Air and Water Through Soils," Journal of Agricultural Soils, Vol. 4, pp. 1-24. Hathaway, G. A. (1945). "Design of Drainage Facilities," Transactions, ASCE, Vol. 110, pp. 697-730. Hicks, W. I. (1944). "A Method of Computing Urban Runoff," Transactions, ASCE, Vol. 109, pp. 1217-1233. Hillel, D. (1971). Soil and Water, Physical Principles and Processes. New York: Academic Press. Horton, R. E. (1919). "Rainfall Interception," Monthly Weather Review, Vol. 47, September, pp. 603-623. Horton, R. E. (1932). "Drainage Basin Characteristics," Transactions, American Geophysical Union, Vol. 13, pp. 350-361. Horton, R. E. (1933). "The Role of Infiltration in the Hydrologic Cycle," Transactions, American Geophysical Union, Vol. 14, pp. 446-460. Horton, R. E. (1941). "Sheet Erosion, Present and Past," Transactions, American Geophysical Union, Vol. 22, pp. 299-305. Houghton, H. G. (1959). "Cloud Physics," Science, Vol. 129, No. 3345, February pp 307-313. Howe, R. H. L. (1960). "The Application of Aerial Photographic Interpretation to the Investigation of Hydrologic Problems," Photogrametric Engineering, Vol. 26, pp. 85-95. Hurst, H. E. (1951). "Long-term Storage Capacity of Reservoirs," Transactions, ASCE, Vol. 116, pp. 770-799. Hurst, H. E. (1956). "Methods of Using Long-term Storage in Reservoirs," Proceedings, Institution of Civil Engineers, London, England, Vol. 5, pt. 1, No. S, September, pp. Hydrometeorological Report No. 39. (1963). "Probable Maximum Precipitation in the Hawaiian Islands." NOAA National Weather Service, Silver Spring, Maryland. Hydrometeorological Report No. 42. (1966). "Meteorological Conditions for the Probable Maximum Flood on the Yukon River Above Rampart, Alaska, " NOAA National Weather Service, Silver Spring, Maryland. Hydrometeorological Report No. 49. (1977). "Probable Maximum Precipitation Estimates, Colorado River and Great Basin Drainages," NOAA National Weather Service, Silver Spring, Maryland. Hydrometeorological Report No. 50. (1981). ''Meteorology of Important Rainstorms in the Colorado River and Great Basin Drainages," NOAA National Weather Service, Silver Spring, Maryland. Hydrometeorological Report No. 51. (1978). "Probable Maximum Precipitation Estimates, United States East of the 105th Meridian," NOAA National Weather Service, Silver Spring, Maryland. Hydrometeorological Report No. 52. (1982). "Application of Probable Maximum Precipitation Estimates--United States East of the 105th Meridian," NOAA National Weather Service, Silver Spring, Maryland. Hydrometeorological Report No. 53. (1980). "Seasonal Variation of 10-Square Mile Probable Maximum Precipitation Estimates, United States East of the 105th Meridian," NOAA National Weather Service, Silver Spring, Maryland. Hydrometeorological Report No. 54. (1983). "Probable Maximum Precipitation and Snowmelt Criteria for Southeast Alaska," NOAA National Weather Service, Silver Spring, Maryland. Hydrometeorological Report No. 55A. (1988). "Probable Maximum Precipitation Estimates United States Between the Continental Divide and the 103rd Meridian," NOAA National Weather Service, Silver Spring, Maryland. Hydrometeorological Report No. 56. (1986). "Probable Maximum and TVA Precipitation Estimates With Areal Distribution for Tennessee River Drainages Less Than 3,000 Mi2 in Area," NOAA National Weather Service, Silver Spring, Maryland. Hydrometeorological Report No. 57. (1994). "Probable Maximum Precipitation- acific Northwest States: Columbia River (including portions of Canada), Snake River, and Pacific Coastal Drainages," NOAA National Weather Service, Silver Spring, Maryland. Hydrometeoroiogicai Report No. 58. (1997). "Probable Maximum Precipitation in California," NOAA National Weather Service, Silver Spring, Maryland. Kennedy, E. 1. (1984). "Discharge Ratings at Gaging Stations," U.S. Geological Survey, Techniques oj Water Resources Investigations, Book 3, Chapter A10. Kirpich, Z. P. (1940). "Time of Concentration of Small Agricultural Watersheds," Civil Engineering, Vol. 10, June, p. 362. Klemes, V. (1974). "The Hurst Phenomenon: A Puzzle?" Water Resources Research, Vol 10, No.4, pp. 675-688. Knapp, B. J. (1978). "Infiltration and Storage of Soil Water," in Hillslope Hydrology, M. J. Kirkby, ed. New York: John Wiley. Kohler, M. A., T. J. Nordenson, and W. E. Fox. (1955). "Evaporation from Pans and Lakes," Weather Bureau, U.S. Department of Commerce, Research Paper No. 38. Kohler, M. A., and M. M. Richards. (1962). "Multicapacity Basin Accounting for PredictIng Runoff from Storm Precipitation," Journal of Geophysical Research, Vol. 67, pp. 5187-5197. Lamoreaux, W. W. (1962). "Modern Evaporation Formula Adapted to Computer Use," Monthly Weather Review, Vol. 90, No. 1, pp. 26-28. Langbein, W. B., et al. (1947). "Topographic Characteristics of Drainage Basins," U.S. Geological Survey Water Supply Paper No. 968-C. Linsley, R. K. , M. A. Kohler, and 1. L. H. Paulhus. (1982). Hydrology for Engineers. 3d. Ed. New York: McGraw-Hill. Meyer, A. F. (1915). "Computing Runoff from Rainfall and Other Physical Data," Transactions, ASCE, Vol. 79, pp. 1056-1224. Meyer, A. F. (1944). "Evaporation from Lakes and Reservoirs," Minnesota Resources Commission, St. Paul, Minnesota, June. Monteith, J. L. (1959). "The Reflection of Short Wave Radiation by Vegetation," Quarterly Journal oj the Royal Meteorological Society, Vol. 85, pp. 586-592. Monteith, J. L. (1965). "Evaporation and the Environment," Symp. Soc. Expl. Biol., Vol. 19, pp. 205-234 . NOAA National Weather Service. (1972). "National Weather Service River Forecast System. Forecast Procedures," Technical Memorandum NWS-HYDRO 14, Dec. , pp. 3.1-3.14. NOAA National Weather Service. (1973). "Atlas 2: Precipitation Atlas of the Western United States." NOAA National Weather Service. (1977). "Five- to 60-Minute Precipitation Frequency for the Eastern and Central United States," Technical Memorandum NWS HYDRO-35. Osmolski, Z. (1985). "Estimating Potential Evapotranspiration from Climatological Data in an Arid Environment," Ph.D. Diss., School of Renewable and Natural Resources, University of Arizona, Tucson. Overton, D. E. , and M. E. Meadows. (1976). Stormwater Modeling. New York: Academic Press. Papadakis, C. N., and M. N. Kazan. (1987). "Time of Concentration in Small Rural Watersheds," Proceedings of the Engineering Hydrology Symposium, ASCE, Williamsburg, Virginia, August 3-7, pp. 633-638. Paulhus, J. L. H., and M. A. Kohler. (1952). "Interpolation of Missing Precipitation Records," Monthly Weather Review, Vol. 80, No. 8, August, pp. 129-133. Penman, H. L. (1948). "Natural Evaporation from Open Water, Bare Soil and Grass," Proceedings of the Royal Society, London, Vol. 193, pp. 120-145. Penman, H. L. (1952). "The Physical Basis of Irrigation Control," Proceedings, 13th International Horticulture Congress, London. Philip, I. R. (1957), (1958). "The Theory of Infiltration," Soil Science, Vol. 83, 1957, pp. 345-357; and 1958, pp. 435-458. Priestley, C. H. B., and R. J. Taylor. (1972). "On the Assessment of Surface Heat Flux and Evaporation Using Large Scale Parameters," Monthly Weather Review, Vol. 100, pp. 81-92 . Ragunath, H. M. (1985). Hydrology. New Delhi: Halsted Press. Rippl, W. (1883). "The Capacity of Storage Reservoirs for Water Supply," Proceedings, Institution oj Civil Engineers, London, England, Vol. 71, pp. 270-278. Salas, J. D., J. W. Delleur, V. Yevjevich, and W. L. Lane. (1980). Applied Modeling of Hydrologic Time Series. Littleton, Colo.: Water Resources Publications. Sartor, D. (1954). "A Laboratory Investigation of Collision Efficiencies, Coalescence and Electrical Charging of Simulated Cloud Particles," Journal of Meteorology, Vol. 11, No. 2, April, pp. 91-103. Schroeder, M. J., and C. C. Buck. (1970). "Fire Weather," Agriculture Handbook 360, Forest Service. Schumm, S. A. (1956). "Evolution of Drainage Systems and Slopes in Perth Amboy, New Jersey," Geological Society of America Bulletin, Vol. 67, pp. 597-646. Shuttleworth, W. J., and J. S. Wallace (1984). "Evaporatlon from Sparse Crops-An Energy Combination Theory," Quarterly Journal of the Royal Meteorological Society, Vol. 111, pp. 839-855. Shuttleworth, W. J. (1993). "Evaporation," Maidment, ed., McGraw-Hill, New York. Stanhill, G. (1975). "The Concept of Potential Evapotranspiration in Arid-Zone Agriculture," Proceedings, Montpelier Symposium in Arid Zone Research, UNESCO, Paris, Vol. 25, pp. 109-171. Tholin, A. L. , and C. J. Keifer. (1960). "The Hydrology of Urban Runoff," Transactions, ASCE, Vol. 125, pp. 1308-1379. Thornthwaite, C. W., H. G. Wilm, et al. (1944). "Report of The Committee on Transpiration and Evaporation, 1943-1944," Transactions, American Geophysical Union, Vol. 25, pt. V, pp. 683-693 . USDA Soil Conservation Service. (1985). National Engineering Handbook. No. 4: Hydrology, Washington, D.C. U.S. Geological Survey. (1952). "Water Loss Investigations: Vol. I-Lake Hefner Studies, Circular No. 229. U.S. Geological Survey. (1954). "The Water Budget Control," in Water Loss Investigations, Lake Hefner Studies, ProfessiOnal Paper No. 269. Viessman, W., J. W. Knapp, G. L. Lewis, and T. E. Harbaugh. (1977). Introduction to Hydrology. 2d. ed. New York: Harper & Row. Weather Bureau, U.S. Department of Commerce. (1955). "Rainfall Intensity-Duratlon-Frequency Curves," Technical Paper No. 25. Weather Bureau, U.S. Department of Commerce. (1962). "Generalized Estimates of Probable Maximum Precipitation and Rainfall Frequency Data for Puerto Rico and Virgin Islands for Areas to 400 Square Miles, Durations to 24 Hours, and Return Periods from 1 to 100 Years," Technical Paper No. 42. Weather Bureau, U.S. Department of Commerce. (1962). "Rainfall Frequency Atlas of Hawaiian Islands for Areas to 200 Square Miles, Durations to 24 Hours, and Return Periods from 1 to 100 Years," Technical Paper No. 43. Weather Bureau, U.S. Department of Commerce. (1963). "Rainfall Frequency Atlas of the United States for Durations from 30 Minutes to 24 Hours and Return Periods from 1 to 100 Years," Technical Paper No. 40. Weather Bureau, U.S. Department of Commerce. (1963). "Probable Maximum Precipitation and Rainfall Frequency Data for Alaska for Areas to 400 Square Miles, Durations to 24 Hours, and Return Periods from 1 to 100 Years," Technical Paper No. 47. Weather Bureau, U.S. Department of Commerce. (1964). "Two-to-Ten Day Precipitation for Return Periods of 2 to 100 Years in the Contiguous United States," Technical Paper No. 49. Yevjevich, V. (1972). Stochastic Processes in Hydrology, Fort Collins, Colo.: Water Resources Publications. http://engineeringhydrology.sdsu.edu 190226 09:45