|
|
|
CAPÍTULO 4: HIDROLOGÍA DE CUENCAS PEQUEÑAS |
|
"Roll waves are possible in the neighborhood of a uniform flow regime only when the Seddon celerity exceeds the Lagrange celerity."
"Olas rollo son posibles en las cercan&iaacute;s de un régimen de flujo uniforme
|
|
This chapter deals with the hydrology of small catchments. It is divided into two sections. Section 4.1 describes the rational method and its application to urban storm drainage design. Section 4.2 discusses overland flow theory and applications. The choice of method is one scale, aided by individual preference and experience. Este capítulo trata de la hidrología de cuencas pequeñas. Se divide en dos secciones. Sección 4.1 se describe el método racional y su aplicación al diseño de drenaje urbano. Sección 4.2 discute la teoría de flujo superficial y aplicaciones. La elección del método es una escala, con la ayuda de preferencia y experiencia individual. |
4.1 EL MÉTODO RACIONAL
|
|
Small Catchments / Pequeñas Cuencas
A small catchment is described by the following features:
Una pequeña cuenca se describe mediante las siguientes características:
Storm rainfall can be assumed to be uniformly distributed in time,
Las precipitaciones tormenta pueden asumirse que están uniformemente distribuidas en el tiempo,
Storm rainfall can be assumed to be uniformly distributed in space,
Las precipitaciones tormenta pueden asumirse que están uniformemente distribuidas en el espacio,
Storm duration typically exceeds time of concentration,
La duración de la tormenta típicamente excede tiempo de concentración,
Runoff is primarily by overland flow, and
La escorrentía es principalmente por el flujo superficial, y
Channel slopes are steep enough so that channel storage processes are negligible.
Las pendientes del canal son bastante empinadas, así que los procesos de almacenamiento del canal son insignificantes.
A catchment possessing some or all of the above properties is small in a hydrologic sense. Its runoff response may be described using relatively simple parametric or empirical methods, which lump all the relevant hydrologic processes into a few key descriptors such as rainfall intensity and catchment area. When increased detail is required, small catchments may be analyzed using the more complex overland flow techniques, which can be either spatially lumped (the conceptual storage model, or storage concept) or distributed (a deterministic model of the kinematic or diffusion wave types). For routine applications, all that is usually required is the simple parametric approach. Exceptions may be warranted in certain specialized applications, e.g., when coupling water quantity and water quality models.
Una cuenca de captación que posea alguna o todas las propiedades anteriores es pequeña en un sentido hidrológico. Su respuesta de la escorrentía puede describirse utilizando métodos paramétricos o empíricos relativamente simples, que engloban todos los procesos hidrológicos pertinentes en unos descriptores clave como la intensidad de la lluvia y el área de influencia. Cuando se requiere un mayor detalle, las cuencas pequeñas pueden ser analizadas usando las técnicas más complejas de flujo superficial, que pueden ser espacialmente englobadas (el modelo de almacenamiento conceptual, o concepto de almacenamiento) o distribuido (un modelo determinista de los tipos de onda cinemática o difusión). Para aplicaciones de rutina, todo lo que normalmente se requiere es el enfoque paramétrico simple. Las excepciones pueden justificarse en ciertas aplicaciones especializadas, por ejemplo, cuando el acoplamiento de modelos de cantidad de agua y la calidad del agua.
It is difficult to set the upper limit of a small catchment without being arbitrary to some degree. Given the natural variability in catchment slopes, vegetation cover, and so on, no single value is universally applicable. In practice, both time of concentration and catchment area have been used to define the upper limit of a small catchment. Some authorities regard a catchment with a time of concentration of 1 h or less as a small catchment. For others, a catchment of 2.5 km2 or less is considered small. Any such limit is bound to be arbitrary, reflecting the accumulated body of experience in runoff response.
Es difícil establecer el límite superior de una pequeña cuenca sin ser arbitrario en algún grado. Teniendo en cuenta la variabilidad natural en las laderas de captación, la cubierta vegetal, y así sucesivamente, sin valor único es de aplicación universal. En la práctica, tanto el tiempo de la concentración y el área de captación se han utilizado para definir el límite superior de una pequeña captación. Algunas autoridades consideran una cuenca con un tiempo de concentración de 1 h o menos como una pequeña cuenca. Para otros, una cuenca de 2.5 km2 o menos es considerada pequeña. Dicho límite está destinada a ser arbitraria, lo que refleja el cuerpo acumulado de experiencia en respuesta escorrentía.
Rational Method / Método Racional
The rational method is the most widely used method for the analysis of runoff response from small catchments. It has particular application in urban storm drainage, where it is used to calculate peak runoff rates for the design of storm sewers and small drainage facilities. The popularity of the rational method is attributed to its simplicity, although reasonable care is necessary in order to use the method effectively.
El método racional es el método más utilizado para el análisis de la respuesta de la escorrentía de las cuencas pequeñas. Cuenta con una aplicación particular en drenaje pluvial urbano, donde se utiliza para calcular las tasas de escorrentía pico para el diseño de alcantarillas y pequeñas instalaciones de drenaje. La popularidad del método racional se atribuye a su simplicidad, aunque un cuidado razonable es necesario con el fin de utilizar el método de eficacia.
The rational method takes into account the following hydrologic characteristics or processes:
El método racional tiene en cuenta las siguientes características o procesos hidrológicos:
- Rainfall intensity,
Intensidad de la lluvia,
- Rainfall duration,
Duración de lluvia,
- Rainfall frequency,
Frecuencia de las precipitaciones,
- Catchment area,
Área de captación,
- Hydrologic abstractions,
Abstracciones hidrológicas,
- Runoff concentration, and
Concentración de la escorrentía, y
- Runoff diffusion.
Difusión de escorrentía.
In general, the rational method provides only a peak discharge, although in the absence of runoff diffusion it is possible to obtain an isosceles-triangle-shaped runoff hydrograph. The peak discharge is the product of:
En general, el método racional proporciona sólo una descarga máxima, aunque en ausencia de difusión de escorrentía es posible obtener un hidrograma de escorrentía en forma de triángulo isósceles. El caudal máximo es el producto de:
- Runoff coefficient,
Coeficiente de escorrentía,
- Rainfall intensity, and
Intensidad de la lluvia, y
- Catchment area.
Área de captación.
All processes are lumped into these three parameters. Rainfall intensity contains information on rainfall duration and frequency. In turn, rainfall duration is related to time of concentration, i.e., to the runoff concentration properties of the catchment. The runoff coefficient accounts for hydrologic abstractions and runoff diffusion, and may also be used to account for frequency. In this way, all the major hydrologic processes responsible for runoff response are embodied in the rational formula.
Todos los procesos se agrupan en estos tres parámetros. La intensidad de la lluvia contiene información sobre la duración y la frecuencia de las precipitaciones. A su vez, la duración de las precipitaciones se relaciona con el tiempo de la concentración, es decir, a las propiedades de concentración de escorrentía de la cuenca. El coeficiente de escurrimiento representa abstracciones hidrológicas y difusión de escorrentía, y también puede ser utilizado para tener en cuenta la frecuencia. De esta manera, todos los principales procesos hidrológicos responsables de la respuesta de escorrentía están incorporados en la fórmula racional.
The rational method does not take into account the following characteristics or processes:
El método racional no toma en cuenta las siguientes características o procesos:
- Spatial or temporal variations in either total or effective rainfall,
Las variaciones espaciales o temporales, ya sea en la precipitación total o efectiva,
- Time of concentration much greater than storm duration, and
Tiempo de concentración mucho mayor que la duración de tormenta, y
- A significant portion of runoff occurring in the form of streamflow.
Una parte significativa de la escorrentía que ocurre en la forma de caudal.
In addition, the rational method does not explicitly account for the catchment's antecedent moisture condition; however, the latter may be implicitly accounted for by varying the runoff coefficient.
Además, el método racional no tiene en cuenta de manera explícita la condición de humedad antecedente de la cuenca; sin embargo, este último puede explicarse implícitamente mediante la variación del coeficiente de escorrentía.
The above conditions dictate that the rational method be restricted to small catchments. To start, the assumption of constant rainfall in space and time can only be justified for small catchments. Furthermore, in a small catchment, storm duration typically exceeds the time of concentration. Finally, in a small catchment, surface runoff processes are usually dominated by overland flow.
Las condiciones anteriores dictan que el método racional se limita a pequeñas cuencas de captación. Para empezar, la asunción de la lluvia constante en el espacio y el tiempo sólo puede justificarse para las pequeñas cuencas de captació. Además, en una pequeña captación, la duración de la tormenta típicamente excede el tiempo de concentración. Por último, en una pequeña cuenca, los procesos de escorrentía superficial son generalmente dominados por flujo superficial.
There is no consensus regarding the upper limit of a small catchment. Values ranging from 0.625 to 12.5 km2 have been quoted in the literature [2, 26]. The current trend is to use 1.25 to 2.5 km2 as the upper limit for the applicability of the rational method. There is no theoretical lower limit, however, and catchments as small as 1 ha or less may be analyzed by the rational method.
No hay consenso respecto del límite superior de una pequeña cuenca de captación. Los valores que van desde 0.625 a 12.5 km2 han sido citados en la literatura [2, 26]. La tendencia actual es usar 1.25 a 2.5 km2 como el límite superior para la aplicabilidad del método racional. No hay un límite inferior teórico, sin embargo, y las cuencas de captación tan pequeñas como 1 ha o menos puede ser analizada por el método racional.
The rational method is based on the following formula:
El método racional se basa en la siguiente fórmula:
| Qp = C I A | (4-1) |
in which Qp = peak discharge corresponding to a given rainfall intensity, duration, and frequency; C = runoff coefficient, a dimensionless empirical coefficient related to the abstractive and diffusive properties of the catchment; I = rainfall intensity, averaged in time and space; and A = catchment area.
en el que Qp = caudal máximo correspondiente a una intensidad de precipitación dada, duración y frecuencia; C = coeficiente de escorrentía, un coeficiente empírico sin dimensión relacionada con las propiedades abstractivos y difusivos de la cuenca; I = intensidad de la lluvia, promediado en el tiempo y espacio; y A = área de influencia.
In SI Units, for rainfall intensity in millimeters per hour, catchment area in square kilometers, and peak discharge in cubic meters per second, the formula for the rational method is the following:
En unidades SI, por la intensidad de las precipitaciones en milímetros por hora, área de influencia en kilómetros cuadrados, y el caudal máximo en metros cúbicos por segundo, la fórmula para el método racional es la siguiente:
| Qp = 0.2778 C I A | (4-2) |
For rainfall intensity in millimeters per hour, catchment area in hectares, and peak discharge in liters per second, the formula is:
Por la intensidad de las precipitaciones en milímetros por hora, zona de influencia en hectáreas y caudal máximo en litros por segundo, la fórmula es:
| Qp = 2.778 C I A | (4-3) |
In U.S. Customary units, for rainfall intensity in inches per hour, catchment area in acres, and peak discharge in cubic feet per second, the formula is:
En las unidades de costumbre en EE.UU., por la intensidad de las precipitaciones en pulgadas por hora, área de influencia en acres y descarga máxima en pies cúbicos por segundo, la fórmula es:
| Qp = 1.008 C I A | (4-4) |
The unit conversion coefficient 1.008 is usually neglected on practical grounds.
El coeficiente de conversión de unidades 1.008 pasa a menudo desapercibida por motivos prácticos.
Methodology / Metodología
The first requirement of the rational method is that the catchment be small. Once the size requirement has been met, the three components of the formula are evaluated. The catchment area is determined by planimetering or other suitable means. Boundaries may be established from topographic maps or aerial photographs. The drainage area survey should also include:
El primer requisito del método racional es que la cuenca sea pequeña. Una vez que se ha cumplido el requisito de tamaño, se evalúan los tres componentes de la fórmula. El área de captación está determinada por planimetría u otros medios adecuados. Los límites pueden establecerse a partir de mapas topográficos o fotografías aéreas. La encuesta del área de drenaje también debe incluir:
Land use and land use changes,
Cambios del uso de la tierra y del suelo,
Percentage of imperviousness,
Porcentaje de impermeabilidad,
Characteristics of soil and vegetative cover that may affect the runoff coefficient, and
Las características de los suelos y la cubierta vegetal que pueden afectar el coeficiente de escorrentía, y
General magnitude of ground slopes and catchment gradient necessary to determine time of concentration.
La magnitud general de las pendientes del terreno y del gradiente de captación necesaria para determinar el tiempo de la concentración.
The evaluation of rainfall intensity is a function of several factors. First, it is necessary to determine the time of concentration. Normally, this is accomplished either:
La evaluación de la intensidad de la lluvia es una función de varios factores. En primer lugar, es necesario determinar el tiempo de concentración. Normalmente, esto se logra ya sea:
By using an empirical formula,
Mediante el uso de una fórmula empírica,
By assuming a flow velocity based on hydraulic properties and calculating the travel time through the catchment's hydraulic length, or
Suponiendo una velocidad de flujo basado en las propiedades hidráulicas y calculando el tiempo de viaje a través de la longitud hidráulica de la cuenca, o
By calculating the steady equilibrium flow velocity (using the Manning equation) and associated travel time through the hydraulic length.
Mediante el cálculo de la velocidad de flujo constante de equilibrio (utilizando la ecuación de Manning) y tiempo de viaje asociado a través de la longitud hidráulica.
Procedures to calculate time of concentration are not very well defined, often involving crucial assumptions such as flow level, channel shape, friction coefficients, and so on. Nevertheless, a value of time of concentration can usually be developed for practical use.
Los procedimientos para calcular el tiempo de concentración no están muy bien definidos, a menudo con supuestos cruciales tales como el nivel de flujo, forma de canal, coeficientes de fricción, y así sucesivamente. Sin embargo, un valor de tiempo de concentración por lo general puede ser desarrollado para el uso práctico.
For urban storm-sewer design, time of concentration at a point is the sum of two parts:
Para el diseño de drenaje pluvial urbano, el tiempo de concentración en un punto es la suma de dos partes:
- Inlet time, and
El tiempo de entrada, y
- Time of flow in the storm sewer up to that point.
Tiempo de flujo en la tormenta de alcantarillado hasta ese momento.
Inlet time is the longest time required for runoff to flow over the catchment surface to the nearest sewer inlet (Fig. 4-1). Time of flow in the sewer, from inlet to point of interest, is calculated using hydraulic flow formulas.
El tiempo de entrada es el tiempo más largo requerido para que la escorrentía fluya sobre la superficie de captación a la entrada de la alcantarilla más cercana (Fig. 4-1). Tiempo de flujo en la alcantarilla, desde la entrada al punto de interés, se calcula utilizando las fórmulas de flujo hidráulico.
Figure 4-1 Urban drainage inlet (University of Suth Queensland, Australia). / Entrada de drenaje urbano (Universidad del Sur de Queensland, Australia). |
Once time of concentration has been determined, the design storm duration is made equal to the time of concentration. This amounts to an assumption of concentrated catchment flow (Section 2.4). Subsequently, a rainfall frequency applicable to the given design condition is chosen. Frequencies (and return periods) vary with the type of project and degree of protection desired. Commonly used return periods are:
Una vez que el tiempo de concentración se ha determinado, la duración de la tormenta de diseño se hace igual al tiempo de la concentración. Esto equivale a una suposición de flujo de captación concentrado (Sección 2.4). Posteriormente, se elige una frecuencia de precipitaciones aplicable a la condición de diseño dada. Frecuencias (y períodos de retorno) varían en función del tipo de proyecto y el grado de protección deseado. Los períodos de retorno más utilizados son:
- 5 to 10 y for storm sewers in residential areas,
5 a 10 años para las alcantarillas de tormenta en áreas residenciales,
- 10 to 50 y for storm sewers in commercial areas, and
10 a 50 años para las alcantarillas de tormenta en las áreas comerciales, y
- 50 to 100 y for regional flood protection works.
50 a 100 años para las obras de protección contra inundaciones regionales.
The size and importance of the project, as well as design criteria established by federal, state and local agencies, have a bearing in the selection of design frequency. The longer the return period (i.e., the smaller the frequency), the greater the peak discharge calculated by the rational formula.
El tamaño y la importancia del proyecto, así como los criterios de diseño establecidos por las agencias federales, estatales y locales, tienen una influencia en la selección de frecuencia de diseño. El más largo es el período de retorno (es decir, cuanto menor es la frecuencia), mayor es el caudal máximo calculado por la fórmula racional.
Rainfall frequency versus peak flow frequency. The question of whether rainfall frequency and peak flow frequency are equivalent is an elusive one. The rational method bases the calculation of peak flow on a chosen rainfall frequency. In nature, however, the frequencies of storms and floods are not necessarily the same, largely due to the effect of antecedent moisture condition, variability in channel transmission losses, overbank storage, and the like. In practice, runoff coefficients are usually adjusted upward to reflect postulated decreases in runoff frequency. This procedure, while empirical, has seemed to work well.
La frecuencia de las precipitaciones frente a la frecuencia de flujo máximo. La cuestión de si la frecuencia de las precipitaciones y la frecuencia de flujo máximo sean equivalentes no es fácil. El método racional basa el cálculo del flujo máximo en una frecuencia de precipitaciones elegido. En la naturaleza, sin embargo, las frecuencias de las tormentas y las inundaciones no son necesariamente los mismos, en gran parte debido al efecto de la condición antecedente de humedad, la variabilidad en las pérdidas de transmisión de canal, el almacenamiento del flujo fuera de los bancos, y similares. En la práctica, los coeficientes de escorrentía son generalmente ajustados hacia arriba para reflejar una disminución en la frecuencia de la escorrentía que se ha postulado. Este procedimiento, si bien empírica, ha parecido que funciona bien.
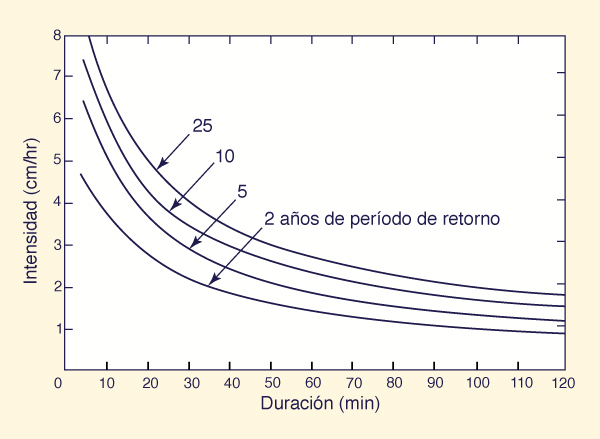
Once rainfall duration and frequency have been determined, the corresponding rainfall intensity is obtained from the appropriate intensity-duration-frequency (IDF) curve. An example of IDF curve is shown in Fig. 4-2. The applicable curve can usually be obtained from cognizant government agencies. Where IDF curves are nonexistent, they can be developed from regional isopluvial maps containing depth-duration-frequency data. These maps are published by the National Weather Service [20, 21, 28].
Una vez que la duración y la frecuencia de las lluvias se han determinado, la intensidad de la lluvia correspondiente se obtiene a partir de la curva de intensidad-duración-frecuencia apropiada (IDF). Un ejemplo de curva IDF se muestra en la Fig. 4-2. La curva de aplicación puede usualmente obtener de las agencias gubernamentales competentes. Donde las curvas IDF son inexistentes, que se pueden desarrollar a partir de mapas isopluvial regionales que contengan datos de profundidad-duración-frecuencia. Estos mapas son publicados por el Servicio Meteorológico Nacional [20, 21, 28].
Figure 4-2 Una curva de intensidad-duración-frecuencia. |
Due to the hyperbolic nature of the intensity-duration curve, an error in rainfall duration causes an error of opposite sign in rainfall intensity. For instance, if the rainfall duration is too long (i.e., time of concentration too long), the calculated rainfall intensity will be too low, and vice versa.
Debido a la naturaleza hiperbólica de la curva de intensidad-duración, un error en la duración de precipitaciones provoca un error de signo opuesto en la intensidad de lluvia. Por ejemplo, si la duración de precipitaciones es demasiado larga (es decir, el tiempo de concentración demasiado largo), la intensidad de lluvia calculada será demasiado baja, y viceversa.
Once rainfall intensity and catchment area have been obtained, a runoff coefficient applicable to the given design condition is selected.
Runoff coefficients are theoretically restricted in the range
Una vez obtenidos la intensidad de la lluvia y el área de influencia, se selecciona un coeficiente
de escorrentía aplicable a la condición de diseño dado. Los coeficientes de
escorrentía son teóricamente restringidos en el rango
- Hydrologic abstractions, and
Abstracciones hidrológicas, y
- Runoff diffusion.
Difusión de escorrentía.
In urban drainage design, hydrologic abstractions include interception, infiltration, and surface storage (Section 2.2). Runoff diffusion is a measure of the catchment's ability to attenuate the flood peaks (Section 2.4).
En el diseño del drenaje urbano, abstracciones hidrológicas incluyen intercepción, infiltración y almacenamiento en la superficie (Sección 2.2). La difusión de escorrentía es una medida de la capacidad de la cuenca para atenuar los picos de inundación (Sección 2.4).
In essence, the runoff coefficient is the ratio of the actual
(calculated) peak runoff rate to the maximum possible runoff rate.
For C = 1, the calculated peak discharge is equal to the maximum possible discharge.
Typical values of runoff coefficients for a wide variety of conditions are given in design manuals and other reference books; see for instance Tables 4-1 (a) and (b).
These values reflect the reduction in peak runoff that is likely to be produced by a given combination of rainfall abstraction and runoff diffusion.
For instance, in Table 4-1 (a), a lawn with a steep gradient (greater than 7 percent) in a heavy (clayey) soil might have C = 0.3,
but a lawn with a mild gradient (less than 2 percent) in a sandy soil might have C = 0.1, reflecting the prevailing abstractive and diffusive rates.
Furthermore, an asphaltic street (of negligible abstractive capability) might have
En esencia, el coeficiente de escurrimiento es la relación de la velocidad
de la escorrentía pico actual (calculada) a la velocidad de la escorrentía máxima posible.
Para C = 1, el caudal máximo calculado es igual al caudal máximo posible.
Los valores típicos de los coeficientes de escorrentía para una amplia variedad de condiciones
están dadas en los manuales de diseño y otros libros de referencia; véase, por ejemplo,
las Tablas 4-1 (a) y (b).
Estos valores reflejan la reducción de la escorrentía pico que es probable que sea producida
por una determinada combinación de abstracción de precipitaciones y la difusión de escorrentía.
Por ejemplo, en la Tabla 4-1 (a), un césped con una pendiente (mayor de 7 por ciento) en un suelo pesado
(arcilloso) podría tener C = 0.3, pero un césped con un gradiente suave (menos de 2 por ciento) en un suelo arenoso podría tener C = 0.1, lo que refleja las velocidades abstractivas y difusivas predominantes. Por otra parte, una calle de asfalto (de la capacidad de abstracción despreciable) podría tener
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The runoff coefficients shown in Table 4-1 (a) are applicable to storms of 5- to 10-y return period. Less frequent storms (e.g., 50-y return period) require the use of higher coefficients because infiltration and other abstractions have a reduced role for the larger storms. The coefficients shown in Table 4-1 (a) represent average antecedent moisture conditions and are not designed to account for multiple storms, or storms of very long duration. Special design cases usually warrant the use of higher runoff coefficients to simulate the existence of wet antecedent moisture conditions in the catchment. Experimental evidence has shown that runoff coefficients tend to increase from one storm to another occurring shortly thereafter, with runoff coefficients tending to increase with storm duration.
Los coeficientes de escorrentía que se muestran en la Tabla 4-1 (a) son aplicables a las tormentas
de período de retorno de 5 a 10-y. Tormentas menos frecuentes (por ejemplo, período de
retorno de 50-y) requieren el uso de coeficientes más altos debido a la infiltración y
otras abstracciones tienen una función reducida para las tormentas más grandes.
Los coeficientes mostrados en la Tabla 4-1 (a) representan condiciones medias de humedad antecedentes y no están diseñados para tener en cuenta múltiples tormentas, o tormentas de muy larga
duración. Los casos especiales de diseño por lo general justifican el uso de coeficientes
de escorrentía para simular la existencia de las condiciones de humedad antecedentes húmedas en la cuenca. La evidencia experimental ha demostrado que los coeficientes de escorrentía
tienden a aumentar de una a otra tormenta que ocurre poco después, con coeficientes de
escorrentía que tiende a aumentar con la duración de la tormenta.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
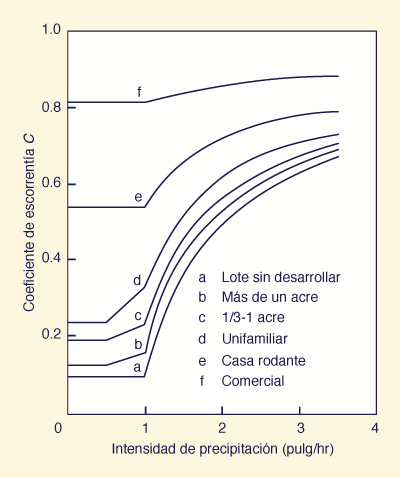
Design values of runoff coefficients are usually a function of rainfall intensity and, therefore, of rainfall frequency. Higher values of runoff coefficient are applicable for higher values of rainfall intensity and return period. A typical C versus I curve is shown in Fig. 4-3 [5]. Alternate ways of expressing the variation of runoff coefficient with rainfall frequency are shown in Figs. 4-4 and 4-5 [6, 25].
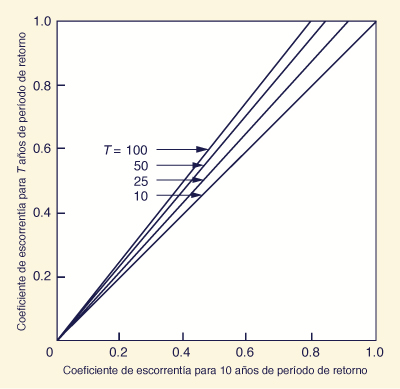
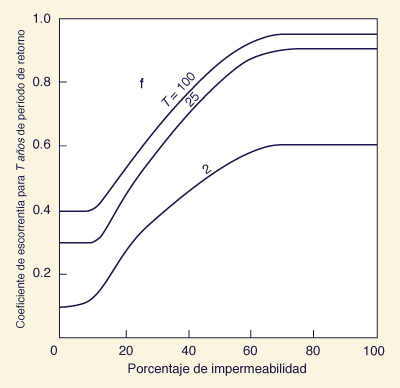
Valores de cálculo de los coeficientes de escorrentía son generalmente una función de la intensidad de la lluvia y, por tanto, de la frecuencia de las precipitaciones. Los valores más altos de coeficiente de escorrentía son aplicables para los valores más altos de intensidad de la lluvia y el período de retorno. Una C típica contra la curva I se muestra en la Fig. 4-3 [5]. Las formas alternativas de expresar la variación del coeficiente de escorrentía con frecuencia de las lluvias se muestran en las figuras. 4.4 y 4.5 [6, 25].
Figure 4-3 Variación del coeficiente de escorrentía con la intensidad de las lluvias [5]. |
Figure 4-4 Variación del coeficiente de escorrentía con frecuencia de precipitaciones [6]. |
Figurq 4-5 Variación del coeficiente de escorrentía con el porcentaje de impermeabilidad y el período de retorno [25]. |
With runoff coefficient, rainfall intensity, and catchment area determined, the peak discharge is calculated by Eq. 4-1. The apparent simplicity of the procedure, however, is misleading. For one thing, there is a range of possible runoff coefficients for each surface condition. Therefore, the chosen C value is usually based on additional field information or designer's experience.
Con coeficiente de escorrentía, intensidad de la lluvia, y el área de influencia determinada, el caudal máximo se calcula por la Ec. 4-1. La simplicidad aparente del procedimiento, sin embargo, es engañosa. Por un lado, hay una gama de posibles coeficientes de escorrentía para cada condición de la superficie. Por lo tanto, el valor C elegido suele basarse en información de campo adicional o experiencia del diseñador.
The effect of frequency and/or antecedent moisture condition needs to be evaluated carefully. Furthermore, there is no absolute certainty that the calculated time of concentration (and, therefore, the rainfall duration) is correct, or even that it remains constant throughout the range of possible frequencies. In fact, since larger flows generally travel with greater velocities (perhaps excepting the case of mild overbank flows, see Fig. 9-3), time of concentration tends to decrease with an increase in return period. Notwithstanding these complexities, the rational method remains a practical way to calculate peak discharge for small catchments based on a few relevant parameters.
El efecto de la frecuencia y / o condición de humedad antecedente debe ser evaluado cuidadosamente. Además, no existe la certeza absoluta de que el tiempo calculado de la concentración (y, por lo tanto, la duración de precipitaciones) sea correcta, o incluso que se mantiene constante durante todo el rango de posibles frecuencias. De hecho, puesto que los flujos más grandes generalmente viajan con mayores velocidades (quizás exceptuando el caso de los flujos de desbordamiento leves, véase Fig. 9-3), el tiempo de concentración tiende a disminuir con el aumento de período de retorno. A pesar de estas complejidades, el método racional sigue siendo una forma práctica para el cálculo del caudal máximo para las pequeñas cuencas en base a unos parámetros pertinentes.
Example 4-1. / Ejemplo 4-1.
Calculate the peak flow Qp by the rational method for the following data: C = 0.6, I =
10 mm/h, and A = 15 ha (hectares). / Calcular el flujo máximo Qp
por el método racional para los siguientes datos: C = 0.6, I = 10 mm/h, y A = 15 ha (hectáreas).
The peak flow is:
El flujo máximo es:
Qp = C I A
Qp = ( 0.6 × 10 mm/h ×
0.001 m/mm × 15 ha × 10000 m2/ha × 1000 L/m3)
/ (3600 s/h) = 250 L/s.
ONLINE CALCULATION. Using the
RATIONAL online calculator,
the peak flow for the given data is: Qp = 250 L/s.
EL CÁLCULO EN LÍNEA. El uso de la calculadora
RACIONAL en línea, el flujo máximo
para los datos dados es: Qp = 250 L/s.
|
Theory of the Rational Method / Teoría del Método Racional
The rational method is based on the principles of runoff concentration and diffusion. For simplicity, the process can be explained in two parts:
El método racional se basa en los principios de concentración de la escorrentía y la difusión. Para simplificar, el proceso puede explicarse en dos partes:
- Concentration without diffusion, and
Concentración sin difusión, y
- Concentration with diffusion.
Concentración con difusión.
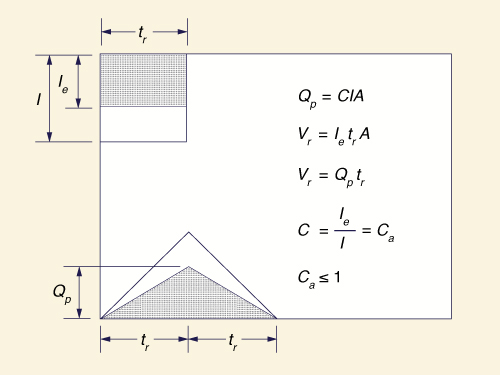
Runoff Concentration Without Diffusion. In the absence of diffusion, a catchment concentrates the flow at the outlet, attaining the maximum possible flow (i.e., the equilibrium flow rate) at the time of concentration. By setting the design rainfall duration equal to the time of concentration, concentrated catchment flow is obtained at the outlet. Since there is no diffusion, the method gives not only a peak flow but also a hydrograph corresponding to that of concentrated catchment flow (Fig. 4-6), with recession time equal to rising time. The runoff coefficient is then simply the ratio of effective rainfall to total rainfall. A mass balance of effective rainfall and runoff leads to:
Concentración de escorrentía sin difusión. En ausencia de difusión, una cuenca concentra el flujo en la salida, alcanzando el flujo máximo posible (es decir, la velocidad de flujo de equilibrio) en el momento de la concentración. Al establecer la duración de precipitaciones de diseño igual al tiempo de concentración, el flujo de captación concentrado se obtiene en la salida. Puesto que no hay difusión, el método proporciona no sólo un flujo máximo sino también un hidrograma correspondiente a la de flujo de captación concentrado (Fig. 4-6), con el tiempo recesión igual al tiempo de ascenso. El coeficiente de escorrentía es simplemente la proporción de precipitación efectiva a la de precipitación total. Un balance de masa de las precipitaciones y la escorrentía efectiva conduce a:
| Vr = Ie tr A = C I A tr | (4-5) |
in which Vr = runoff volume; Ie = effective rainfall; and tr = rainfall duration (either effective or total). Equation 4-5 leads to:
en el que el Vr = volumen de escurrimiento; Ie = precipitación efectiva; y tr = duración de precipitaciones (ya sea efectiva o total). Ecuación 4-5 conduce a:
Ie
|
C = Ca = ___ I | (4-6) |
in which Ca = runoff coefficient due only to abstraction (Ca ≤ 1).
en el que Ca = coeficiente de escorrentía debido sólo a la abstracción (Ca ≤ 1).
Figure 4-6 Rational method: Método racional: concentración de flujo sin difusión. |
Runoff concentration without diffusion is typical of steep catchments, with slopes greater than 0.01, where the momentum balance is dominated by the gravitational and frictional forces. For catchments of milder slope (say, less than 0.001), the role of the flow depth gradient increases, and runoff diffusion becomes increasingly important. In the extreme case, for a hypothetical catchment of zero ground slope, the diffusion effect is theoretically the only one present.
Concentración de escorrentía sin difusión es típico de las cuencas empinadas, con pendientes de más de 0.01, donde el balance de momento está dominado por las fuerzas gravitatorias y de fricción. Para las cuencas de captación de pendiente más suave (por ejemplo, menos de 0.001), el papel del gradiente de profundidad de flujo aumenta, y la difusión de escorrentía se convierte en cada vez más importante. En el caso extremo, por una cuenca hipotética de la pendiente del punto cero, el efecto de difusión es teóricamente el único presente.
Runoff Concentration With Diffusion.
When diffusion is present, the rational method accounts for it in the runoff coefficient.
Thus, the runoff coefficient is used to model not only abstraction but also diffusion.
Diffusion modifies the catchment response in such a way as to increase the recession time and decrease the peak flow.
Therefore, a hydrograph shape can no longer be obtained directly from a mass balance as in the
case of runoff concentration without diffusion.
The lack of a hydrograph shape does not impede the use of the rational method,
because the diffusion can be represented directly in the peak flow formula, by lowering the runoff
coefficient below that due only to abstraction
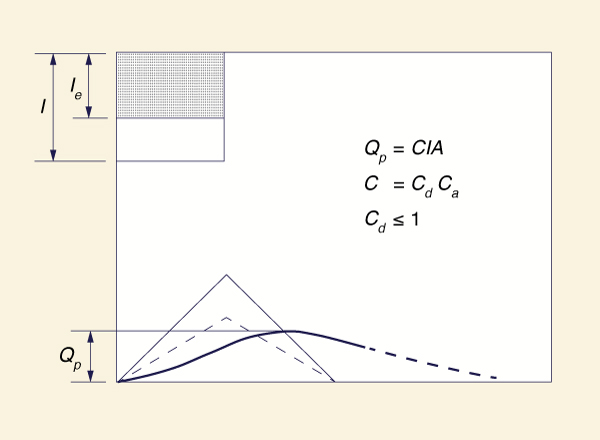
La concentración de escorrentía con difusión. Cuando la difusión está presente, el método racional se representa en el coeficiente de escorrentía. Por lo tanto, el coeficiente de escorrentía se utiliza para modelar no sólo la abstracción sino también la difusión. La difusión modifica la respuesta de captación de una manera tal como para aumentar el tiempo de recesión y disminuir el flujo máximo. Por lo tanto, una forma de hidrograma ya no se puede obtener directamente a partir de un balance de masas como en el caso de la concentración de la escorrentía sin difusión. La falta de una forma de hidrograma no impide el uso del método racional, porque la difusión se puede representar directamente en la fórmula de flujo máximo, mediante la reducción del coeficiente de escorrentía abajo que se debe sólo a la abstracción (Fig. 4-7).
The reduction in the runoff coefficient amounts to:
La reducción en el coeficiente de escorrentía asciende a:
| C = Cd Ca | (4-7) |
in which C = runoff coefficient and Cd = component of runoff coefficient accounting only for diffusion (Cd ≤ 1).
en la que C = coeficiente de escorrentía y Cd = componente del coeficiente de escorrentía que representa sólo la difusión (Cd ≤ 1).
Figura 4-7 Método racional: la concentración de flujo con la difusión. |
The question of whether the peak is reached before, at, or after the time of concentration, as
La cuestión de si el pico se alcanza antes, durante o después del tiempo de la concentración, como muestra la Fig. 4-7 (b), es irrelevante, ya que el método no proporciona la forma del hidrograma, limitándose a proporcionar una descarga máxima.
In the absence of diffusion, Cd = 1 and C = Ca.
Likewise, in the absence of abstraction, Ca = 1 and
En ausencia de la difusión, Cd = 1 y C = Ca.
Del mismo modo, en ausencia de la abstracción, Ca = 1 and
In practice, no quantitative distinction is made between the abstractive and diffusive components of the runoff coefficient. Usage, however, reflects the fact that runoff diffusion is implicitly being considered; see, for instance, the marked change in runoff coefficient with surface slope shown in Table 4-1.
En la práctica, no se hace distinción cuantitativa entre los componentes abstractivos y difusivos del coeficiente de escorrentía. El uso, sin embargo, refleja el hecho de que la difusión de escorrentía está siendo considerada implícitamente; váase, por ejemplo, el marcado cambio en el coeficiente de escorrentía con pendiente de la superficie se muestra en la Tabla 4-1.
Further Developments / Nuevos desarrollos
Attempts to analyze the behavior of the rational method have led to the concept of peak flow per unit area [27]:
Los intentos de analizar el comportamiento del método racional han llevado al concepto de flujo máximo por unidad de superficie [27]:
Qp
|
qp = ____ = C I A | (4-8) |
in which qp = peak flow per unit area. Rainfall intensity varies with rainfall duration and frequency. Likewise, runoff coefficient also varies with rainfall duration and frequency. Therefore, a relation linking peak flow per unit area to rainfall duration and frequency can be obtained:
en el que qp = flujo máximo por unidad de área. La intensidad de precipitaciones varían con la duración de las precipitaciones y de la frecuencia. Del mismo modo, el coeficiente de escorrentía también varía con la duración y la frecuencia de las precipitaciones. Por lo tanto, una relación que une el flujo máximo por unidad de área a la duración y la frecuencia de precipitaciones se pueden obtener:
| qp = f ( tr, T ) | (4-9) |
in which T = return period.
en la que T = período de retorno.
Another approach is based on expressing the rational formula in the following form:
Otro enfoque se basa en la expresión de la fórmula racional en la forma siguiente:
Qp
|
C = _____ I A | (4-10) |
where now the runoff coefficient may be interpreted as dimensionless peak flow, or peak flow per unit area per unit rainfall intensity. It follows that dimensionless peak flow is related to the abstractive and diffusive properties of the catchment.
donde ahora el coeficiente de escorrentía puede ser interpretado como el flujo máximo adimensional, o de flujo máximo por unidad de superficie por unidad de intensidad de las precipitaciones. De ello se deduce que el flujo máximo adimensional se relaciona con las propiedades abstractivas y difusivas de la cuenca.
A similar concept is used in the Natural Resources Conservation Service TR-55 method (Section 5.3). In this method, a unit peak flow is defined as the peak flow per unit area per unit rainfall depth. In the TR-55 graphical method included, the unit peak flow is a function of time of concentration, abstraction parameter, and temporal storm pattern. The fact that unit peak flow is a function of temporal storm pattern qualifies the TR-55 graphical method as an extension of the rational method to midsize catchments. While no upper limit to catchment size is indicated, the method is restricted to a time of concentration less than or equal to 10 h.
Un concepto similar se utiliza en el Método TR-55 del Servicio de Conservación de Recursos Naturales (Sección 5.3). En este método, una unidad de flujo máximo se define como el flujo máximo por unidad de área por unidad de profundidad de precipitaciones. En el método gráfico TR-55 se incluye, la unidad de flujo máximo es una función del tiempo de concentración, el parámetro de abstracción, y el patrón de tormenta temporal. El hecho de que la unidad de flujo máximo es una función del patrón de la tormenta temporal califica el método gráfico TR-55 como una extensión del método racional para las cuencas de tamaño medio. Mientras no se indique ningún límite superior al tamaño de la cuenca, el método se limita a un tiempo de concentración inferior o igual a 10 h.
Applications of the Rational Method / Aplicaciones del Método Racional
Relation Between Runoff Coefficient and φ-index. The runoff coefficient can be related to total rainfall intensity and φ-index, provided the following assumptions are satisfied:
Relación entre el coeficiente de escorrentía y φ-índice. El coeficiente de escorrentía puede estar relacionado con la intensidad de la precipitación total y φ-índice, proporcionó los siguientes supuestos que se cumplen:
- Catchment response occurs under negligible diffusion, and
La respuesta de captación se produce bajo la difusión despreciable, y
- Total and effective rainfall intensities are constant in time.
Las intensidades totales y efectivas de precipitaciones son constantes en el tiempo.
The first assumption is valid for steep catchments, whereas the second assumption is implicit in the application of the rational method. For catchment response without diffusion:
La primera hipótesis es válida para cuencas empinadas, mientras que el segundo supuesto está implícito en la aplicación del método racional. Para una respuesta de captación sin difusión:
Ie
|
C = Ca = ___ I | (4-11) |
For constant rainfall intensities:
Para intensidades de precipitaciones constantes:
| Ie = I - φ | (4-12) |
Combining Eqs. 4-11 and 4-12:
Combinando las ecuaciones. 4-11 y 4-12:
I - φ
|
C = _________ I | (4-13) |
Areal Weighing of Runoff Coefficients. Values of runoff coefficients may vary within a given catchment. When a clear pattern of variation is apparent, a weighted value of runoff coefficient should be used. For this purpose, the individual subareas are delineated and their respective runoff coefficients are identified. The weighted value is obtained by weighing the runoff coefficients in proportion to their respective subareas. This leads to:
Ponderación aérea de los Coeficientes de Escorrentía. Los valores de los coeficientes de escorrentía pueden variar dentro de una cuenca determinada. Cuando un patrón claro de variación es aparente, se debe utilizar un valor ponderado del coeficiente de escorrentía. Para este propósito, las subáreas individuales están delineadas y sus respectivos coeficientes de escorrentía se identifican. El valor ponderado se obtiene ponderando los coeficientes de escorrentía en proporción a sus respectivas subáreas. Esto lleva a:
|
Qp = 0.2778 I Σ ( Ci Ai ) i | (4-14) |
in which Ci = runoff coefficient of i th subarea and Ai = drainage area of i th subarea. Applicable units are those of Eq. 4-2.
en el que Ci = coeficiente de escorrentía de orden i subárea y Ai = área de drenaje de orden i subárea. Unidades aplicables son las de la Ec. 4-2.
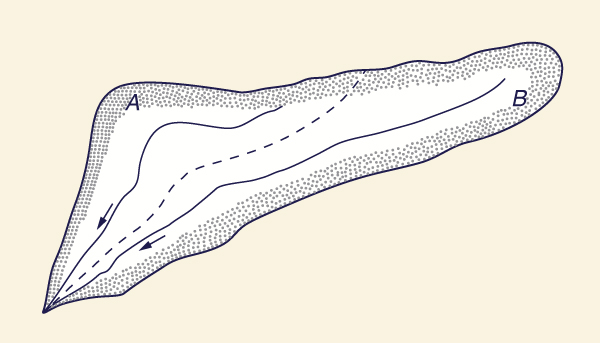
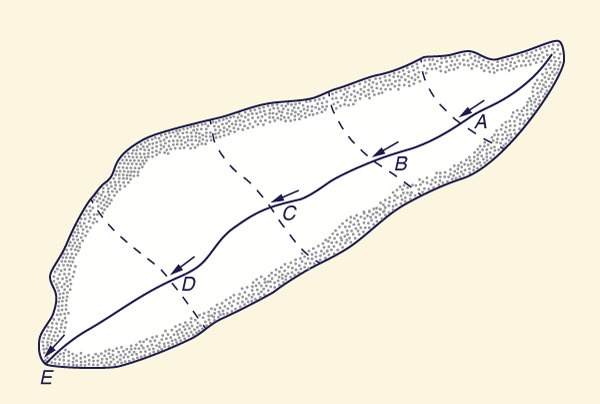
Composite Catchments. A composite catchment is one that drains two or more adjacent subareas of widely differing characteristics. For instance, assume that a catchment has two subareas A and B with times of concentration tA and tB, respectively, with tA being much less than tB (Fig. 4-8).
Las cuencas compuestas. Una cuenca compuesta es una que drena dos o más subáreas adyacentes de características muy diferentes. Por ejemplo, supongamos que una cuenca tiene dos subáreas A y B con tiempos de concentración tA y tB, respectivamente, con tA siendo mucho menos que tB (Fig. 4-8).
Figure 4-8 Rational method: A composite catchment. / Figura 4.8 Método Racional: Una cuenca compuesta. |
To apply the rational method to this composite catchment, several rainfall durations are chosen, ranging from tA to tB. in suitable increments. The calculation proceeds by trial and error, with each trial associated with each rainfall duration. To calculate the partial contribution from subarea B, an assumption must be made regarding the rate at which the flow is concentrated at the catchment outlet. The rainfall duration that gives the highest combined peak flow (A plus B ) is taken as the design rainfall duration. The procedure is illustrated by the following example.
Para aplicar el método racional a esta cuenca compuesta, varias duraciones de precipitaciones son elegidos, que van desde tA a tB. en incrementos adecuados. El cálculo procede por ensayo y error, con cada ensayo asociado con cada duración de las precipitaciones. Para el cálculo de la contribución parcial de la subárea B, se debe hacer una suposición sobre la velocidad a la que el flujo se concentra en la salida de la cuenca. La duración de las precipitaciones que da el caudal máximo combinado más alto (A más B) se toma como la duración de diseño de precipitaciones. El procedimiento se ilustra mediante el siguiente ejemplo.
Example 4-2. / Ejemplo 4-2.
Calculate the peak discharge by the rational method for a 1-km2 composite catchment with the following characteristics:
Calcular el caudal máximo por el método racional para una cuenca compuesta
de 1-km2 con las siguientes características:
Assume a return period T = 10 y and the following IDF function:
Asumir un período de retorno T = 10 y la siguiente función de las IDF:
1000T 0.2
in which I = rainfall intensity, in millimeters per hour; T = return period, in years; and tr = rainfall duration, in minutes.
To compute the contribution of subarea B, assume that the flow concentrates linearly at the outlet, i.e., each equal increment of time causes an equal increment of area contributing to the flow at the outlet.
en la que I = intensidad de las precipitaciones, en milímetros por hora;
T = período de retorno, en años; y
tr = duración de precipitaciones, en minutos.
Para calcular la contribución de la subárea B, se supone que el flujo se concentra linealmente en la salida, es decir, cada incremento igual de tiempo provoca un incremento igual de área que contribuye
al flujo en la salida.
First, choose rainfall durations between 20 min and 60 min at 10-min intervals.
For each rainfall duration, rainfall intensity is calculated by Eq. 4-15.
The assumption of linear concentration for subarea B leads to the following:
En primer lugar, seleccionar las duraciones de las precipitaciones entre 20 min y 60 min a intervalos de 10 min.
Para cada duración de precipitaciones, la intensidad de las precipitaciones se calcula por la Ec. 4-15.
La suposición de la concentración lineal por subárea B conduce a lo siguiente:
For tr = 20 min, the peak flow is (Eq. 4-14):
Para tr = 20 min, el flujo máximo es (Ec. 4-14.):
Successive trials for rainfall durations of 30, 40, 50, and 60 min result in lower peak flows.
Therefore, the peak flow is 9.986 m3/s and the design rainfall duration is 20 min.
Los ensayos sucesivos para duraciones de precipitaciones de 30, 40, 50, y 60 min
resulta en flujos máximos más bajos. Por lo tanto,
el flujo máximo es 9.986 m3/s, y la duración de las
precipitaciones de diseño es de 20 min.
ONLINE CALCULATION. Using the
ONLINE
RATIONAL COMPOSITE calculator,
the peak flow for the given data is: Qp = 9.9856 m3/s.
CÁLCULO EN LÍNEA. Usando la calculadora
COMPUESTO RACIONAL EN LÍNEA
el flujo máximo para el dato dado es: Qp = 9.9856 m3/s.
|
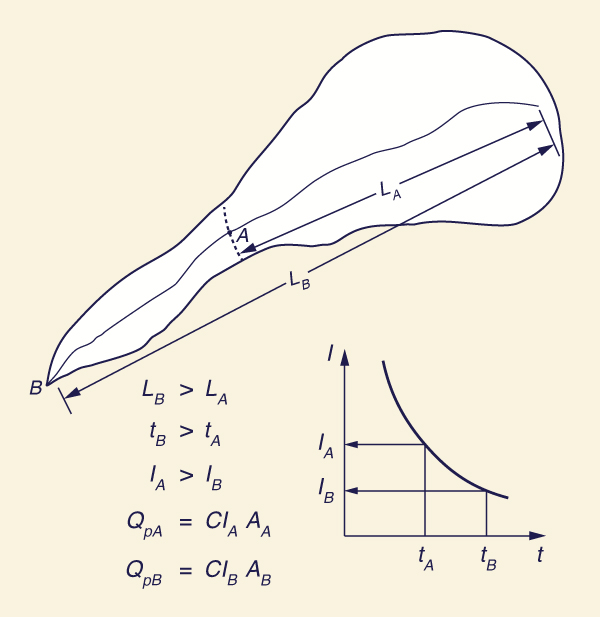
Effect of Catchment Shape. The rational method is suited to catchments where drainage area increases more or less linearly with catchment length. If this is not the case, the peak flow may not increase with an increase in catchment area. To illustrate, take the catchment shown in Fig. 4-9. The time of concentration to point A is tA; the time of concentration to point B is tB; and tB is greater than tA. Therefore, IA is greater than IB.
Efecto de la forma de captación. El método racional se adapta a las cuencas donde el área de drenaje aumenta más o menos linealmente con la longitud de captación. Si este no es el caso, el flujo máximo no puede aumentar con un aumento en el área de captación. Para ilustrar, tome la cuenca que se muestra en la Fig. 4-9. El tiempo de concentración al punto A is tA; el tiempo de concentración al punto B es tB; y tB es mayor que tA. Por lo tanto, IA es mayor que IB.
Figure 4-9 Rational method: Effect of catchment shape / Figura 4.9 Método Racional: Efecto de la forma de captación |
The drainage area to point A is AA, and the drainage area to point B is AB, and AB is greater than AA. Assuming the same runoff coefficient for the partial area (to point A) and the total area (to point B), the peak flow at A is: QpA = CIAAA. Likewise, the peak flow at B is: QpB = CIBAB. For QpB to be greater than QpA, it is necessary that (AB / AA) be greater than (IA / IB). In other words, the drainage area must grow in the downstream direction at least as fast as the decrease in corresponding rainfall intensity. Otherwise, the peak discharge at A would be greater than that at B. The situation is illustrated by the following example.
El área de drenaje al punto A es AA, y el área de drenaje al punto B es AB, y AB es mayor que AA. Suponiendo el mismo coeficiente de escorrentíla de la zona parcial (al punto A) y el área total (al punto B), el flujo máximo en A es: QpA = CIAAA. Igualmente, el flujo máximo en B is: QpB = CIBAB. Para QpB sea mayor que QpA, es necesario que (AB / AA) sea mayor que (IA / IB). En otras palabras, el área de drenaje debe crecer en la dirección aguas abajo al menos tan rápido como la disminución de la correspondiente intensidad de lluvia. De lo contrario, el caudal máximo en A sería mayor que en B. La situación se ilustra mediante el siguiente ejemplo.
Example 4-3. / Ejemplo 4-3.
Assume that the drainage area at A (Fig. 4-9) has a time of concentration such that the applicable rainfall intensity is 50 mm/h, and that from point A to point B the time of concentration increases, thereby decreasing the
applicable rainfall intensity for the drainage area at B to 40 mm/h.
Assume that the drainage area at A = 0.8 km2 and at B = 0.9 km2.
Compute the peak flow at points A and B. Assume C = 0.5.
Suponer que el área de drenaje en A (Fig. 4-9) tiene un tiempo de concentración
tal que la intensidad de la precipitación aplicable es de 50 mm / h, y que desde el punto A
al punto B el tiempo de concentración aumenta, disminuyendo así
la intensidad de la precipitación aplicable para el área de drenaje en
B a 40 mm/h. Suponer que el área de drenaje en
A = 0.8 km2 and at B = 0.9 km2.
Calcule el flujo máximo en los puntos A and B. Asumir C = 0.5.
The peak flow at A is (Eq. 4-2): QpA = 0.278 × 0.5 × 50 × 0.8 = 5.56 m3/s.
The peak flow at B is: QpB =
El flujo máximo en A es (Ec. 4-2): QpA = 0.278 × 0.5 × 50 × 0.8 = 5.56 m3/s.
El flujo máximo en B is: QpB = |
Modified Rational Method. The application of the rational method to large urban catchments, i.e., those featuring well-defined conveyance channels and drainage areas greater than 1.3 km2 but less than 2.5 km2, requires special techniques. For one thing, the flow is likely to vary widely along the main channel, ranging from small at the upstream reaches to larger at the downstream reaches. In this case, it may be difficult to determine an average value of time of concentration.
Método Racional Modificado. La aplicación del método racional a grandes cuencas urbanas, es decir, aquellos con canales de transporte bien definidos y áreas de drenaje mayor que 1.3 km2 pero menos de 2.5 km2, requiere técnicas especiales. Por un lado, es probable que varíe ampliamente a lo largo del canal principal, que van desde pequeños en los tramos aguas arriba a mayor en los tramos aguas abajo del flujo. En este caso, puede ser difícil determinar un valor promedio de tiempo de concentración.
An alternative is to apply the rational method incrementally, using a technique known as the modified rational method. The method requires the subdivision of the catchment into several subcatchments, as shown in Fig. 4-10. First, the time of concentration tA is estimated and used to calculate the peak flow QpA at A, using Eq. 4-2. With the aid of open channel flow formulas, QpA is conveyed through the main channel from A to B, and the travel time tAB calculated. The time of concentration, tB = tA + tAB, is used to calculate the peak flow QpB at B, again using Eq. 4-2. The procedure continues in the downstream direction until the peak flow QpE is calculated. If the runoff coefficients are different for each subcatchment, Eq. 4-14 can be used in lieu of Eq. 4-2. While the procedure is relatively straightforward, it may result in peak flows decreasing in the downstream direction (due to the effect of catchment shape).
Una alternativa es aplicar el método racional de forma incremental, utilizando una técnica conocida como el método racional modificado. El método requiere la subdivisión de la cuenca de captación en varias subcuencas, como se muestra en la Fig. 4-10. En primer lugar, el tiempo de concentración tA se estima y se utiliza para calcular el flujo máximo QpA en A, usando la Ec. 4-2. Con la ayuda de las fórmulas de flujo de canales abiertos, QpA se transmite a través del canal principal de A a B, y el tiempo de viaje tAB calculado. El tiempo de concentración, tB = tA + tAB, se utiliza para calcular el flujo máximo QpB en B, de nuevo utilizando la Ec. 4-2. El procedimiento continúa en la dirección aguas abajo hasta que el flujo máximo QpE es calculado. Si los coeficientes de escorrentía son diferentes para cada subcuenca, la Ec. 4-14 se puede utilizar en lugar de la Ec. 4-2. Si bien el procedimiento es relativamente sencillo, que puede dar lugar a flujos máximos decrecientes en la dirección aguas abajo (debido al efecto de la forma de captación).
Figure 4-10 Catchment subdivision in the modified rational method. / Figura 4.10 Subdivisión de la cuenca de captación en el método racional modificado. |
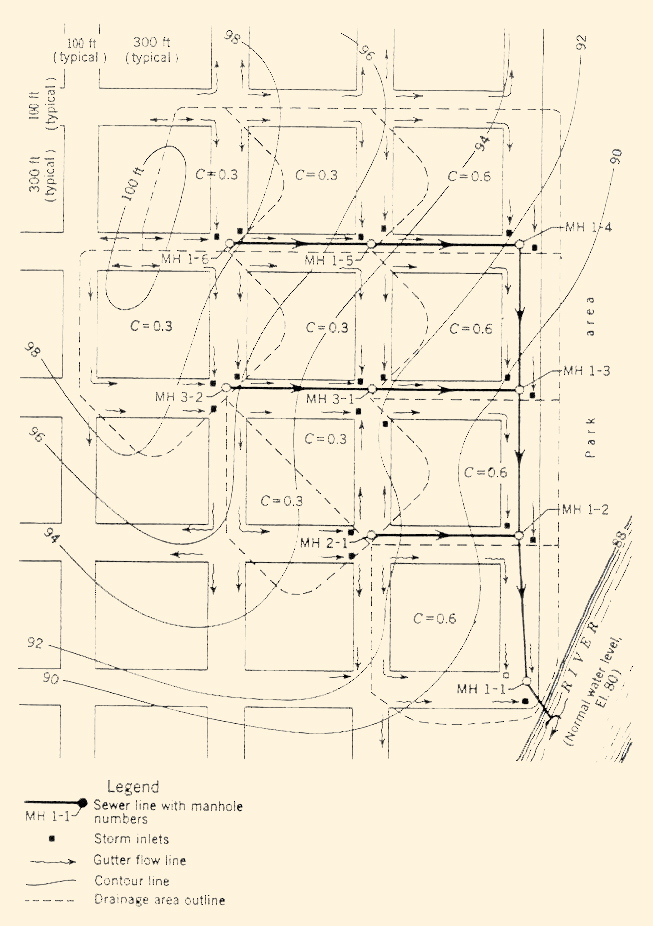
Application to Storm-sewer Design. A typical plan for design of a small storm-sewer project is shown in Fig. 4-11. Table 4-2 shows a summary of the computations illustrating the application of the rational method to determine design flows. The example is based on the following conditions:
Aplicación al Diseño de Dreanje Pluvial. Un plan típico para el diseño de un pequeño proyecto de drenaje pluvial se muestra en la Fig. 4-11. La Tabla 4-2 muestra un resumen de los cálculos que ilustran la aplicación del método racional para determinar los flujos de diseño. El ejemplo se basa en las siguientes condiciones:
- Runoff Coefficients /
Coeficientes de escorrentía
- Resident area / Área residencial: C = 0.3
- Business area / Área de negocios: C = 0.6
- Areal weighing of runoff coefficients where required. / Ponderación superficial de los coeficientes de escorrentía donde se requiera.
- Intensity-Duration-Frequency curve shown in Fig. 2-12 (a). Selected design frequency: 5 y.
La curva de intensidad-duración-frecuencia se muestra en la Fig. 2-12 (a). Frecuencia de diseño seleccionada: 5 y.
- Inlet time: 20 min.
Tiempo de entrada: 20 min.
- Manning n in sewer: 0.013.
Manning n en alcantarilla: 0.013.
- Free outfall to river at elevation 80.
Desagüe libre al río en la elevación 80.
-
A drop of 0.1 ft across each manhole where no change in pipe size occurs (to account for head losses).
When a change in pipe size occurs, set the elevation of 0.8 of pipe depths equal, and provide corresponding fall in manhole invert.
(Note: In larger systems, a more rigorous analysis of hydraulic losses through manholes, transitions, and changes in direction is required for adequate hydraulic design).
Una caída de 0.1 pies a través de cada pozo de registro, donde ningún cambio ocurre en el tamaño de la tubería (a la cuenta de pérdidas de carga). Cuando se produce un cambio en el tamaño de la tubería, ajuste la elevación de 0.8 de las profundidades de tubería iguales, y proporcionar una caída correspondiente en el pozo de registro invertido. (Nota: En los sistemas más grandes, se requiere un análisis más riguroso de las pérdidas hidráulicas a través del pozo de registro, transiciones y cambios de dirección para el diseño hidráulico adecuado).
Figure 4-11 Typical storm-sewer design plan [2]. / Figura 4-11 Plan de diseño de drenaje pluvial típica [2]. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This example is extracted from Design and Construction of Sanitary and Storm Sewers, ASCE Manual of Engineering Practice No. 37, 1960 [2].
Este ejemplo se extrae de Design and Construction of Sanitary and Storm Sewers, ASCE Manual of Engineering Practice No. 37, 1960 [2].
4.2 FLUJO DE SUPERFICIE
|
|
Overland flow is surface runoff that occurs in the form of sheet flow on the land surface without concentrating in clearly defined channels. This type of flow is the first manifestation of surface runoff, since the latter occurs first as overland flow before it has a chance to flow into channels and become streamflow.
Flujo superficial es la escorrentía superficial que se produce en forma de flujo laminar en la superficie de la tierra sin concentrarse en los canales claramente definidos. Este tipo de flujo es la primera manifestación de la escorrentía superficial, ya que este último se produce por primera vez como flujo superficial antes de que tenga la oportunidad de fluir en los canales y convertirse en el caudal.
Overland flow theory uses deterministic methods to describe surface runoff in overland flow planes. The theory is based on established principles of fluid mechanics such as laminar and turbulent flow, mass and momentum conservation, and unsteady free surface flow. The spatial and temporal description leads to differential equations and to their solution by either analytical or numerical means. For certain applications, simplified conceptual models can be developed for practical use.
La teoría del flujo superficial utiliza métodos deterministas para describir la escorrentía superficial en planos de flujo superficial. La teoría se basa en los principios establecidos de la mecánica de fluidos, tales como flujo laminar y turbulento, la masa y conservación del momento, y el flujo superficial libre inestable. La descripción espacial y temporal conduce a las ecuaciones diferenciales y de su solución ya sea por medios analíticos o numéricos. Para ciertas aplicaciones, los modelos conceptuales simplificados pueden ser desarrollados para su uso práctico.
Overland flow theory seeks to find an answer to the problem of catchment response: What is the hydrograph that will be produced at a catchment's outlet, subject to a given effective rainfall? In overland flow applications, effective rainfall is also referred to as rainfall excess. Unlike the rational method, which generally does not produce a hydrograph, overland flow models have the capability to account not only for runoff concentration but also for runoff diffusion. Another advantage of overland flow models is their distributed nature, i.e., the fact that rainfall excess can be allowed to vary in space and time if necessary. Overland flow models, then, are a more powerful tool than parametric models such as the rational method. However, the complexity increases in direct relation to their greater level of detail.
La teoría del flujo superficial busca encontrar una respuesta al problema de la respuesta de captación: ¿Cuál es el hidrograma que se producirá en la salida de una cuenca, sujeto a una precipitación efectiva dado? En aplicaciones de flujo superficial, la lluvia efectiva también se conoce como el exceso de precipitaciones. A diferencia del método racional, que por lo general no produce un hidrograma, modelos de flujo por tierra tienen la capacidad de dar cuenta no sólo de la concentración de la escorrentía, sino también para la difusión de escorrentía. Otra ventaja de los modelos de flujo por tierra es su naturaleza distribuida, es decir, el hecho de que el exceso de precipitación se puede permitir que variar en el espacio y el tiempo si es necesario. Modelos de flujo superficial, entonces, son una herramienta más potente que los modelos paramétricos, como el método racional. Sin embargo, la complejidad aumenta en relación directa a su mayor nivel de detalle.
As with the rational method, a question that must be addressed at the outset is the following: What size catchment can be analyzed with overland flow techniques? Here again, the answer is not very well defined. Intuitively, overland flow computations should be applicable to small catchments, primarily because overland flow is the main surface-flow feature of small catchments. The method, however, is not necessarily restricted to small catchments. Midsize catchments may also benefit from the increased detail of overland flow models. The actual limit is a practical one. Computations need to be performed in modules of relatively small size; otherwise, it is likely that the terrain's topographic, frictional, and vegetative features will not be properly represented in the overland flow model. In practice, overland flow techniques are restricted to catchments for which the surface features can be adequately represented within the model's topological structure. Otherwise, the amount of lumping introduced (i.e., temporal and spatial averaging) would interfere with the method's ability to predict the occurrence of flows in a distributed context.
Al igual que con el método racional, una pregunta que debe ser abordado desde el principio es la siguiente: ¿Qué tamaño de captación puede ser analizada con técnicas de flujo superficial? Una vez más, la respuesta no está muy bien definida. Intuitivamente, los cálculos de flujo superficial deben ser aplicables a las pequeñas cuencas, principalmente por el flujo superficial es la función del flujo superficial principal de pequeñas cuencas. El método, sin embargo, no necesariamente se limita a pequeñas cuencas. Las cuencas medianas también pueden beneficiarse del incremento del detalle de los modelos de flujo superficial. El límite real es de carácter práctico. Los cálculos deben realizarse en módulos de tamaño relativamente pequeño; de lo contrario, es probable que la topografía del terreno, fricción, y características vegetativas no estarán representados adecuadamente en el modelo de flujo superficial. En la práctica, las técnicas de flujo superficial se restringen a zonas de captación para los que las características de la superficie pueden ser adecuadamente representados dentro de la estructura topológica del modelo. De lo contrario, la cantidad de formación de grumos introducido (es decir, de promedio temporal y espacial) interferiría con la capacidad del método para predecir la ocurrencia de los flujos en un contexto distribuido.
Overland flow techniques often form part of computer models that simulate all relevant phases of the hydrologic cycle. These models use overland flow techniques in their catchment routing component. The fundamentals of overland flow theory are presented here. Catchment routing methods are described in Chapter 10.
Las técnicas de flujo superficial a menudo forman parte de modelos informáticos que simulan todas las fases pertinentes del ciclo hidrológico. Estos modelos utilizan técnicas de flujo superficial en sus componentes de enrutamiento de captación. Los fundamentos de la teoría de flujo superficial se presentan aquí. Los métodos de enrutamiento de captación se describen en el Capítulo 10.
Overland Flow Theory / Teoría del Flujo Superficial
The mathematical description of overland flow begins with the equation of mass conservation of fluid mechanics, also referred to as the continuity equation.
In one-dimensional flow, this equation states that the change in flow per unit length
in a control volume is balanced by the change in fiow area per unit time:
La descripción matemática del flujo superficial comienza con la ecuación de conservación de la masa de mecánica de fluidos, también conocido como la ecuación de continuidad. En el flujo unidimensional, esta ecuación establece que el cambio en el flujo por unidad de longitud en un volumen de control es equilibrada por el cambio en el área de flujo por unidad de tiempo:
∂Q ∂A
| ____ + ____ = 0 ∂x ∂t | (4-16) |
This equation does not include sources or sinks. Inclusion of the latter leads to:
Esta ecuación no incluye las fuentes o sumideros. La inclusión de este último conduce a:
∂Q ∂A
| ____ + ____ =
qL ∂x ∂t | (4-17) |
in which qL = lateral inflow or outflow (inflow positive, outflow negative), or net lateral flow per unit length, in L2 T -1 units.
en el que qL = flujo de entrada lateral o de salida (flujo de entrada positiva, la salida negativa), o flujo lateral neta por unidad de longitud, en unidades L2 T -1.
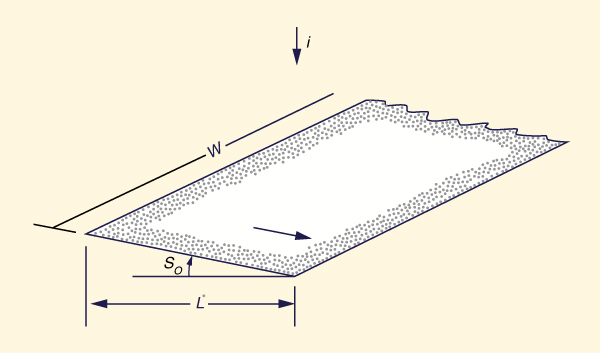
In small catchment hydrology, overland flow is assumed to take place on the overland flow plane. This is a plane of length L (in the flow direction), slope So, and of sufficiently large width W (Fig. 4-12). Therefore, a unit-width analysis is appropriate. For a unit width, Eq. 4-17 is converted to:
En hidrología de cuencas pequeñas, se supone que el flujo superficial que tendrá lugar en el plano de flujo superficial. Este es un plano de longitud L (en la dirección de flujo), la pendiente So, y suficientemente de gran anchura W (Fig. 4-12). Por lo tanto, un análisis de ancho unitario es apropiado. Para una unidad de anchura, Ec. 4-17 se convierte en:
∂q ∂h
| ____ + ____ =
i ∂x ∂t | (4-18) |
in which q = flow rate per unit width; h = flow depth; and i = lateral inflow (rainfall excess), or inflow per unit area, in L T -1 units. While lateral inflow can vary in time and space, a first approximation is to consider it constant.
en el que q = velocidad de flujo por unidad de ancho; h = profundidad de flujo; y i = entrada lateral (exceso de lluvia), o entrada de flujo por unidad de área, en unidades L T -1. Mientras el flujo de entrada lateral puede variar en el tiempo y el espacio, en una primera aproximación consiste en considerarlo constante.
Figure 4-12 Overland flow plane. / Plano de flujo superficial. |
Flow over the plane. Flow over the plane can be described as follows: As excess rainfall begins, water accumulates on the plane surface and begins to flow out of the plane at its lower end. Flow at the outlet (i.e., the outflow) increases gradually from zero, while the total volume of water stored over the plane also increases gradually. Eventually, if rainfall excess continues, both outflow and total volume of water stored over the plane reach a constant value. These constants are referred to as equilibrium outflow and equilibrium storage volume. For continuing rainfall excess, outflow and storage volume remain constant and equal to the equilibrium value. Immediately after excess rainfall ceases, outflow begins to draw water from storage, gradually decreasing while depleting the storage volume. Eventually, outflow returns to zero as the storage volume is completely drained.
Flujo sobre el plano. Flujo sobre el plano se puede describir como sigue: Cuando comienza el exceso de lluvias, el agua se acumula sobre la superficie plana y comienza a fluir fuera del plano en su extremo inferior. El flujo en la salida (es decir, el flujo de salida) aumenta gradualmente desde cero, mientras que el volumen total de agua almacenada sobre el plano también aumenta gradualmente. Finalmente, si el exceso de precipitaciones continúa, tanto en la salida y el volumen total de agua almacenada sobre el plano alcanza un valor constante. Estas constantes se denominan flujo de salida de equilibrio y el volumen de almacenamiento de equilibrio. Para continuar el exceso de lluvia, la salida y el volumen de almacenamiento se mantienen constantes e igual al valor de equilibrio. Inmediatamente después de que cese el exceso de precipitaciones, la salida comienza a sacar agua de almacenamiento, disminuyendo gradualmente mientras que agotan el volumen de almacenamiento. Con el tiempo, la salida vuelve a cero como el volumen de almacenamiento está completamente agotada.
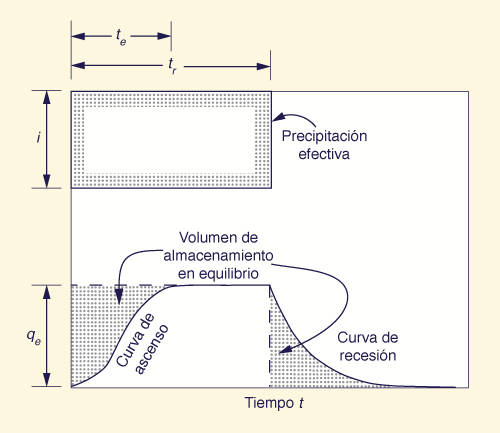
The process is depicted in Fig. 4-13. The flow from start to equilibrium is called the rising limb of the overland flow hydrograph. The flow from equilibrium back to zero is called the receding limb of the hydrograph. The equilibrium outflow can be calculated by recognizing that at equilibrium state, the outflow must equal the inflow (i.e., rainfall excess). Therefore,
El proceso se representa en la Fig. 4-13. El flujo desde el principio al equilibrio se llama curva ascendente del hidrograma del flujo superficial. El flujo del equilibrio regresa a cero se llama curva de retroceso del hidrograma. El flujo de salida de equilibrio se puede calcular mediante el reconocimiento que en estado de equilibrio, el flujo de salida debe ser igual al flujo de entrada (es decir, exceso de lluvia). Por consiguiente,
|
i qe = ( _______ ) L 3600 | (4-19) |
in which qe = equilibrium outflow, in liters per second per meter; i = rainfall excess, in millimeters per hour; and L = plane length, in meters.
en el que qe = flujo de salida de equilibrio, en litros por segundo por metro; i = exceso de lluvia, en milímetros por hora; y L = longitud del plano, en metros.
Figura 4-13 Plano del hidrograma de flujo superficial. |
Equation 4-19 is essentially a statement of runoff concentration, similar to Eq. 2-58 or to Eq. 4-1 with C = 1. Whether the flow actually does concentrate and reach its equilibrium value will depend upon the duration of the rainfall excess tr relative to the time te required to reach equilibrium. If tr > te, equilibrium is reached.
La ecuación 4-19 es esencialmente una declaración de la concentración de la escorrentía, similar a la Ec. 2-58 o para la Ec. 4-1 con C = 1. Si el flujo en realidad se concentra y alcanza su valor de equilibrio dependerá de la duración del exceso de precipitación relativo tr a el tiempo te requerido para alcanzar el equilibrio. Si tr > te, se alcanza el equilibrio.
The volume of storage is the area below the line q = qe, and above the rising limb of the overland flow hydrograph, as shown in Fig. 4-13. As a first approximation, the shaded area above the rising limb may be assumed to be equal to the area below the rising limb. In this case, the equilibrium storage volume is:
El volumen de almacenamiento es el área debajo de la línea q = qe, y por encima de la curva ascendente del hidrograma de flujo superficial, como se muestra en la Fig. 4-13. Como una primera aproximación, el área sombreada por encima de la curva ascendente puede suponerse que es igual al área por debajo de la curva ascendente En este caso, el volumen de almacenamiento de equilibrio es:
|
qe te Se = ________ 2 | (4-20) |
in which Se = equilibrium storage volume, in liters per meter; qe = equilibrium outflow, in liters per second per meter; and te = time to equilibrium, in seconds.
en el que Se = volumen de almacenamiento de equilibrio, en litros por metro; qe = salida de equilibrio, en litros por segundo por metro; y te = tiempo de equilibrio, en segundos.
In practice, surface and other irregularities cause the equilibrium state to be approached asymptotically and, therefore, the actual time to equilibrium is not clearly defined. A value of time t corresponding to q = 0.98qe may be taken as a practical measure of te. Then, Eq. 4-20 is only an approximation of the actual storage volume.
En la práctica, la superficie y otras irregularidades causan el estado de equilibrio a ser abordado asintóticamente y, por lo tanto, el tiempo real de equilibrio no está claramente definida. Un valor de tiempo t correspondiente a q = 0.98qe puede tomarse como una medida práctica de q = 0.98qe. Entonces, la Ec. 04-20 es sólo una aproximación del volumen de almacenamiento real.
The equation of continuity, Eq. 4-18, can also be expressed in the following form:
La ecuación de continuidad, Ec. 4-18, también se puede expresar de la siguiente forma:
|
1 ∂h u ∂h h ∂u ( ___ ) _____ + ( ____ ) _____ + ( ___ ) _____ = 1 i ∂t i ∂x i ∂x | (4-21) |
in which u = q/h = mean velocity.
en el que u = q/h = velocidad media.
The value of equilibrium outflow was obtained from Eq. 4-19 based on continuity considerations. However, the shape of the rising and receding limbs and the time to equilibrium remain to be elucidated. This can be obtained through the equation of momentum conservation (or equation of motion), following established principles of unsteady open channel flow [3, 9, 18]. The equation of motion, however, is a nonlinear partial differential equation. A form of this equation with u and h as dependent variables is [18]:
El valor de flujo de salida de equilibrio se obtuvo de la Ec. 4-19 sobre la base de consideraciones de continuidad. Sin embargo, la forma de las curvas ascendente y retroceso y el tiempo al equilibrio permanecen estar aclarados. Esto se puede obtener a través de la ecuación de conservación del momento (o ecuación de movimiento), siguiendo los principios establecidos de flujo de canal abierto inestable [3, 9, 18]. La ecuación de movimiento, sin embargo, es una ecuación diferencial parcial no lineal. Una forma de esta ecuación con u and h como variables dependientes es [18]:
|
1 ∂u u ∂h h ∂u iu ( __ ) ____ + ( __ ) ____ + ( ___ ) ____ + Sf - So + ____ = 0 i ∂ t i ∂x i ∂x gh | (4-22) |
in which Sf = friction slope, So = plane slope, g = gravitational acceleration, and all other terms have been previously defined. All terms in Eqs. 4-21 and 4-22 are dimensionless.
en el que la Sf = pendiente de fricción, So = pendiente plana, g = aceleración de la gravedad, y todos los demás términos se han definido previamente. Todos los términos en las ecuaciones 4-21 y 4-22 son adimensionales.
The solution of Eqs. 4-21 and 4-22 can be attempted in a variety of ways. Analytical solutions are usually based on an assumption of linearity [1, 22]. Numerical solutions have been extensively applied to stream and river flow problems [16, 18]. To date, overland flow problems have been solved with one of the following approaches:
La soluci&oaacute;n de las ecuaciones 4-21 y 4-22 se puede intentar en una variedad de maneras. las soluciones analíticas se basan generalmente en la suposición de linealidad [1, 22]. Las soluciones numéricas se han aplicado ampliamente para los problemas de flujo en arroyos y ríos [16, 18]. Hasta la fecha, los problemas de flujo superficial se han resuelto con uno de los siguientes enfoques:
- Storage concept,
Concepto de almacenamiento,
- Kinematic wave technique,
Técnica de la onda cinemática,
- Diffusion wave technique, and
Técnica de onda de difusión, y
- Dynamic wave technique.
Técnica de onda dinámica.
The storage concept is similar to that used in reservoir routing (Chapter 8). The kinematic wave technique simulates runoff concentration in the absence of diffusion. The diffusion wave technique simulates runoff concentration in the presence of small amounts of diffusion. The dynamic wave technique solves the complete set of governing equations, Eqs. 4-21 and 4-22, including runoff concentration, diffusion, and dispersion (third order) processes [23]. For practical applications, the storage concept and kinematic and diffusion wave techniques can be shown to be useful approximations to the complete equations.
El concepto de almacenamiento es similar al utilizado en el enrutamiento reservorio (capítulo 8). La técnica de onda cinemática simula la concentración de la escorrentía en la ausencia de difusión. La técnica de la onda de difusión simula la concentración de la escorrentía en presencia de pequeñas cantidades de difusión. La técnica de onda dinámica resuelve el conjunto completo de ecuaciones de gobierno, las ecuaciones 4-21 y 4-22, incluyendo los procesos de concentración de la escorrentía, la difusión y dispersión (tercer orden) [23]. Para aplicaciones prácticas, el concepto de almacenamiento y técnicas de onda cinemática y de difusión puede demostrarse que son aproximaciones útiles a las ecuaciones completas.
In principle, the kinematic wave is an improvement over the storage concept; in turn, the diffusion wave is an improvement over the kinematic wave, whereas the dynamic wave is an improvement over the diffusion wave. Invariably, the effort involved in obtaining a solution increases in direct relation to the complexity of the equations being solved, including initial and boundary conditions. The storage and kinematic wave techniques are described in the following sections. A brief introduction to the diffusion wave technique is also given. The dynamic wave solution for overland flow is outside the scope of this ebook [4].
En principio, la onda cinemática es una mejora sobre el concepto de almacenamiento; a su vez, la onda de difusión es una mejora sobre la onda cinemática, mientras que la onda dinámica es una mejora con respecto a la onda de difusión. Invariablemente, el esfuerzo que supone la obtención de una solución aumenta en relación directa con la complejidad de las ecuaciones resueltas, incluidas las condiciones iniciales y de contorno. Las técnicas de almacenamiento y de onda cinemática se describen en las siguientes secciones. También se da una breve introducción a la técnica de ondas de difusión. La solución de onda dinámica de flujo superficial se encuentra fuera del alcance de este libro electrónico [4].
Overland Flow Solution Based on Storage Concept / Solución de flujo superficial basado en el concepto de almacenamiento
Early approaches to solve the overland flow problem are attributed to Horton [10] and Izzard [13, 14]. In particular, Horton noticed that experimental data justified a relationship between equilibrium outflow and equilibrium storage volume of the following form:
Los primeros enfoques para resolver el problema de flujo superficial se atribuyen a Horton [10] e Izzard [13, 14]. En particular, Horton se dio cuenta de que los datos experimentales justifican una relación entre el flujo de salida de equilibrio y el volumen de almacenamiento de equilibrio de la siguiente forma:
| qe = a Sem | (4-23) |
in which a and m are empirical constants. A mean flow depth he is defined in the following way:
en la que a y m son constantes empíricas. Una profundidad de flujo medio he se define de la siguiente manera:
Se
|
he = _____ L | (4-24) |
Combining Eqs. 4-23 and 4-24:
Combinando las ecuaciones 4-23 y 4-24:
| qe = b hem | (4-25) |
in which b = aLm, another constant. The value of the exponent m is a function of flow regime, depending on whether the latter is laminar, turbulent (either Manning or Chezy), or mixed laminar-turbulent. Typical values of m are shown in Table 4-3.
en la que b = aLm, otra constante. El valor del exponente m es una función del régimen de flujo, dependiendo de si el último es laminar, turbulento (ya sea Manning o Chezy), o laminar-turbulento mixto. Los valores típicos de m se muestran en la Tabla 4-3.
| ||||||||||||||||||||||||||||||||||
A conceptual estimate of time to equilibrium can be obtained by combining Eqs. 4-20 and 4-23 and solving for te:
Una estimación conceptual de tiempo para el equilibrio se puede obtener mediante la combinación de las Ecs. 4-20 y 4-23 y despejando te:
|
2 te = ________________ qe (m -1)/m a 1/m | (4-26) |
For laminar flow conditions, b = aLm = CL, where CL is defined as follows [3]:
Para las condiciones de flujo laminar, b = aLm = CL, donde CL se define como sigue [3]:
|
gSo CL = _________ 3 ν | (4-27) |
and ν = kinematic viscosity, a function of water temperature (see Tables A-1 and A-2, Appendix A).
The units of CL are L-1T -1.
Furthermore, with qe = iL, Eq. 4-26 reduces to the following for the case of
y ν = viscosidad cinemática, una función de la temperatura del agua
(véanse las Tablas A-1 y A-2, Apéndice A).
Las unidades de CL son L-1T -1.
Por otra parte, con qe = iL, Ec. 4-26 se reduce a lo siguiente para el caso
de
|
2 L 1/3 te = _____________ i 2/3 CL1/3 | (4-28) |
in which te = time to equilibrium, in seconds; L = length of overland flow plane, in meters; and
en el que te = tiempo de equilibrio, en segundos; L = longitud del plano de flujo superficial, en metros; y
For turbulent Manning flow conditions, b = aLm = (1/n) So1/2, in which n is the Manning friction coefficient. With qe = iL, Eq. 4-26 reduces to the following for the case of mixed laminar-turbulent flow (5/3 < m < 3):
Para las condiciones de flujo turbulentas de Manning, b = aLm = (1/n) So1/2, en la que n es el coeficiente de fricción de Manning. Con qe = iL, la Ec. 4-26 se reduce a lo siguiente para el caso de flujo laminar-turbulento mixto (5/3 < m < 3):
|
2 (nL) 1/m te = ___________________ i (m - 1)/m So 1/(2m) | (4-29) |
with the same units as Eq. 4-28 (te in seconds, L in meters, i in meters per second). As expected, time to equilibrium increases with bottom friction and plane length, and decreases with effective rainfall intensity and plane slope.
con las mismas unidades que la Ec. 4-28 (te en segundos, L en metros, i en metros por segundo). Como era de esperar, el tiempo de equilibrio aumenta con la fricción de fondo y la longitud plana, y disminuye con la intensidad de la precipitación efectiva y pendiente plana.
Equation 4-29 was developed by assuming the Manning formula in the rating. Therefore, it is strictly applicable only to m = 5/3. In practice, however, this equation is also used for mixed laminar-turbulent flow (5/3 < m < 3). In addition, the very shallow depths that usually prevail in overland flow calculations result in a substantial increase in friction. These differences are accounted for by using an effective roughness parameter N in lieu of the Manning friction coefficient [11]. Typical values of N are given in Table 4-4.
La ecuación 4-29 se desarrolló asumiendo la fórmula de Manning en la valoración. Por lo tanto, es estrictamente aplicable sólo para m = 5/3. En la práctica, sin embargo, esta ecuación también se utiliza para el flujo laminar turbulento mixto (5/3 < m < 3). Además, las profundidades muy poco profundas que generalmente prevalecen en cálculos de flujo superficial resultan en un incremento sustancial en la fricción. Estas diferencias se explican por el uso de un parámetro de rugosidad efectiva N en lugar del coeficiente de fricción de Manning [11]. Los valores típicos de N se dan en la Tabla 4-4.
| ||||||||||||||||||||||||||||||||||
Rising limb of the overland flow hydrograph. The Horton-Izzard solution to the overland flow problem is based on the assumption that Eq. 4-23 is valid not only at equilibrium but also at any other time:
La curva de aumento del hidrograma de flujo superficial. La solución Horton-Izzard al problema de flujo superficial se basa en la suposición de que la Ec. 4-23 es válida no sólo en el equilibrio, sino también en cualquier otro momento:
| q = a S m | (4-30) |
in which q = outflow at time t, and S = storage volume at time t. This assumption is convenient because it allows an analytical solution for the shape of the overland flow hydrograph. Equation 4-30 is the formula for a nonlinear reservoir, i.e., a function relating outflow and storage volume in a nonlinear way (m ≠ 1). Therefore, a nonlinear reservoir is being used to model the equation of motion, Eq. 4-22. In essence, a deterministic model (Eq. 4-22) has been replaced by a conceptual model (Eq. 4-30).
en el que q = flujo de salida en el tiempo t, y S = volumen de almacenamiento en el tiempo t. Este supuesto es conveniente porque permite una solución analítica para la forma del hidrograma flujo superficial. La Ecuación 4-30 es la fórmula para un depósito no lineal, es decir, una función que relaciona la salida y el volumen de almacenamiento de una manera no lineal (m ≠ 1). Por lo tanto, un reservorio no lineal se utiliza para modelar la ecuación de movimiento, la Ec. 4.22. En esencia, un modelo determinista (Ec. 4-22) ha sido reemplazado por un modelo conceptual (Ec. 4-30).
Equation 4-16 can be expressed in one space increment Δx to yield:
La Ecuación 4-16 se puede expresar en un incremento de espacio Δx para producir:
|
dS I - O = _____ dt | (4-31) |
in which I = inflow to the control volume, O = outflow from the control volume, and dS/dt = rate of change of storage in control volume (Fig. 4-14).
For the overland flow case, I = iL and
en la que I = flujo de entrada para el volumen de control,
O = flujo de salida del volumen de control, y dS/dt = velocidad de cambio de almacenamiento en el volumen de control (Fig. 4-14). Para el caso de flujo superficial,
I = iL and
|
dS iL - q = _____ dt | (4-32) |
which through Eqs. 4-19, 4-23, and 4-30 leads to:
que a través de las Ecs. 4-19, y 4-30 conduce a:
|
dS a Sem - a S m = ______ dt | (4-33) |
Figure 4-14 Inflow, outflow, and rate of change of storage in a control volume. / Figura 4-14 flujo de entrada, flujo de salida, y la velocidad de cambio de almacenamiento en un volumen de control. |
Integrating Eq. 4-33:
La integración de la ecuación 4-33:
|
1 1 t = ____ ∫ ____________ dS a Se m - S m | (4-34) |
and, through additional algebraic manipulation [1]:
y, a través de la manipulación algebraica adicional [1]:
|
1 1 t = _________________ ∫ ________________ d ( q /qe ) 1/m a 1/m qe (m - 1)/m 1 - ( q /qe ) | (4-35) |
Using Eq. 4-26, Eq. 4-35 reduces to:
Utilizando la Ec. 4.26, la Ec. 4-35 se reduce a:
|
t 1 1 ____ = ___ ∫ ______________ d ( q /qe ) 1/m te 2 1 - ( q /qe ) | (4-36) |
For m = 2, which describes a flow regime that is 75% turbulent (between laminar, for which m = 3, and 100% turbulent Manning, for which m = 5/3), the solution of Eq. 4-36 is:
Para m = 2, el cual describe un régimen de flujo que es 75% turbulento (entre laminar, para el que m = 3, y 100% Manning turbulento, para los que m = 5/3), la solución de la Ec. 4-36 es:
|
t 1 1 + ( q /qe )1/2 ____ = ___ ln [ ___________________ ] te 4 1 - ( q /qe )1/2 | (4-37) |
which was expressed by Horton with time as independent variable as follows [1]:
que se expresó por Horton con el tiempo como variable independiente como la siguiente [1]:
|
q t ____ = tanh 2 [ 2 ( ____ ) ] qe te | (4-38) |
For m = 3 (laminar flow), the solution of Eq. 4-36 is [24]:
Para m = 3 (flujo laminar), la solución de la ecuación 4-36 es [24]:
|
t 1 1 + (q/qe)1/3 + (q/qe)2/3 ___ = ____ ln { __________________________ } te 12 [ (q/qe)1/3 -1 ] 2 |
|
1 π 1 - ______ { ____ + arctan { - _____ [ 1 + 2 (q / qe)1/3 ] } } 2√3 6 √3 | (4-39) |
With the aid of Eq. 4-38, and Eq. 4-19 for qe and Eq. 4-29 for te,
the rising limb of the overland flow hydrograph for m = 2 can be calculated.
Likewise, with the aid of
Con la ayuda de la ecuación. 4-38, y la Ec. 4-19 para qe y la Ec. 4.29 para
te, la curva ascendente del hidrograma de flujo superficial para
m = 2 se puede calcular.
Del mismo modo, con la ayuda de la
Receding limb. For m > 1, the receding limb of the overland flow hydrograph can be calculated by the following formula [24]:
La curva de retroceso. Para m > 1, la curva de retroceso del hidrograma de flujo superficial se puede calcular por la siguiente fórmula [24]:
|
t 1 _____ = ____________ [ (q /qe ) (1 - m )/m - 1 ] te 2 (m - 1) | (4-40) |
where q /qe = 1 for t /te = 0, i.e., the outflow is at equilibrium at the start of the recession.
donde q /qe = 1 para t /te = 0, es decir, el flujo de salida está en equilibrio en el inicio de la recesión.
Likewise, for m = 1, the hydrograph recession is as follows [24]:
Asimismo, para m = 1, la recesión del hidrograma es como sigue [24]:
|
t 1 _____ = _____ ln (q /qe ) te 2 | (4-41) |
where q /qe = 1 for t /te = 0.
donde q /qe = 1 para t /te = 0.
Limitations. Several assumptions limit the applicability of the Horton-Izzard solution. The most important one is the nonlinear form of the storage equation, Eqs. 4-23 and 4-30. Izzard has suggested that the method should be restricted to cases where the product of rainfall intensity (in millimeters per hour) and plane length (in meters) (iL) does not exceed 3000. Notwithstanding the apparent limitations, the Horton-Izzard solution of overland flow has been extensively used in the past, particularly in the design of airport drainage [3, 7].
Limitaciones. Varios supuestos limitan la aplicabilidad de la solución de Horton-Izzard. La más importante es la forma no lineal de la ecuación de almacenamiento, las Ecs. 4-23 y 4-30. Izzard ha sugerido que el método debe limitarse a los casos en que el producto de la intensidad de la lluvia (en milímetros por hora) y la longitud plana (en metros) (iL) no sea superior a 3000. A pesar de las limitaciones aparentes, la solución Horton-Izzard de flujo superficial se ha utilizado ampliamente en el pasado, en particular en el diseño de drenaje de aeropuertos [3, 7].
Overland Flow Solution Based on Kinematic Wave Theory / Solución del Flujo Superficial Basado en la Teoría de la Onda Cinemática
According to this theory, Eq. 4-22 can be approximated by a single-valued flow-depth rating at any point, leading to:
De acuerdo con esta teoría, la Ec. 4.22 se puede aproximar por una valoración de un solo valor de flujo de profundidad en cualquier punto, lo que lleva a:
| q = b h m | (4-42) |
in which b and m are constants analogous to those of Eq. 4-25. Unlike Horton's approach, which bases the rating on the storage volume on the entire plane (Eqs. 4-23 and 4-30), the kinematic wave approach bases the rating on flow depths at individual cross sections. This difference has substantial implications for computer modeling because whereas the Horton approach is lumped in space, the kinematic approach is not, and therefore it is better suited to distributed computation.
en la que b and m son constantes análogos a los de la Ec. 4.25. A diferencia de enfoque de Horton, que se basa en la valoración en el volumen de almacenamiento en todo el plano (Ecs. 4.23 y 4.30), la onda cinemática de aproximación basa la valoración en profundidades de flujo en secciones transversales individuales. Esta diferencia tiene implicaciones sustanciales para el modelado de computadora porque mientras que el enfoque Horton se agrupa en el espacio, el enfoque cinemático no, y por lo tanto es más adecuado para la computación distribuida.
Reservoirs and channels. The difference between a rating based on storage volume and one based on flow depth merits further discussion. There are two distinct features in free surface flow in natural catchments:
Los reservorios y canales. La diferencia entre una clasificación basada en el volumen de almacenamiento y uno basado en la profundidad de flujo merita más discusión. Hay dos características distintas en el flujo de superficie libre en las cuencas naturales:
- Reservoirs, and
Reservorios y
- Channels.
Canales
In an ideal reservoir, the water surface slope is zero [Fig. 4-15 (a)], and, therefore, outflow and storage volume are uniquely related. If an outflow rating is desired, storage volume can be uniquely related to stage; consequently, outflow can be uniquely related to stage and flow depth. On the other hand, in an ideal channel, the water surface slope is nonzero [Fig. 4-15 (b)], and, in general, storage is a nonunique function of inflow and outflow. If a flow rating is desired, the only practical way of obtaining it is to relate flow to its depth.
En un reservorio ideal, el pendiente de la superficie del agua es cero [Fig. 4-15 (a)], y, por lo tanto, la salida del flujo y el volumen de almacenamiento están únicamente relacionados. Si se desea una valoració del flujo de salida, el volumen de almacenamiento puede ser singularmente relacionada con la etapa; en consecuencia, la salida de flujo puede estar únicamente relacionada con el estadio y la profundidad de flujo. Por otra parte, en un canal ideal, la pendiente de la superficie del agua es distinto de cero [Fig. 4-15 (b)], y, en general, el almacenamiento es una función no única del flujo de entrada y salida. Si se desea una clasificación de flujo, la única manera práctica de obtenerlo es relacionar el flujo a su profundidad.
Figure 4-15 (a) Ideal reservoir; (b) ideal channel. / Figura 4-15 (a) Reservorio Ideal; (b) el canal ideal. |
In the Horton approach, outflow is related to storage volume and, by extension, to the mean flow depth on the overland plane. In contrast, in the kinematic wave approach, outflow is related to the outflow depth. Since the typical overland flow problem has a nonzero water surface slope, it is more likely to behave as a channel rather than a reservoir. Therefore, it would appear that the kinematic wave approach is a better model of the physical process than the storage concept. Further analysis has shown, however, that while the kinematic wave lacks diffusion, the storage concept does not. In this sense, the storage concept may well be a better model than the kinematic wave approach for cases featuring significant amounts of runoff diffusion.
En el enfoque Horton, el flujo de salida está relacionada con el volumen de almacenamiento y, por extensión, a la profundidad media de flujo en el plano suprficial. Por el contrario, en el enfoque de onda cinemática, el flujo de salida está relacionada con la profundidad flujo de salida. Dado que el problema típico de flujo superficial tiene una pendiente superficial del agua distinto de cero, es más probable que se comporte como un canal en lugar de un reservorio. Por lo tanto, parecería que el enfoque de onda cinemática es un modelo mejor del proceso físico que el concepto de almacenamiento. Un análisis más detallado ha demostrado, sin embargo, que mientras que la onda cinemática carece de difusión, el concepto de almacenamiento no. En este sentido, el concepto de almacenamiento bien puede ser un modelo mejor que el enfoque de la onda cinemática para casos que ofrecen cantidades significativas de difusión de escorrentía.
The kinematic wave assumption, Eq. 4-42, amounts to substituting a uniform flow formula (such as Manning's) for the equation of motion, Eq. 4-22. In essence, it says that as far as momentum is concerned, the flow is steady. The unsteadiness of the phenomena, however, is preserved through the continuity equation, Eq. 4-18, or Eq. 4-21. The implication of the kinematic wave assumption is that unsteady flow may be visualized as a succession of steady uniform flows, with the water surface slope remaining constant at all times. This, of course, can be reconciled with reality only if the flow unsteadiness is very mild; that is, if the changes in stage occur very gradually.
La suposición de onda cinemática, la Ec. 4-42, equivale a la sustitución de una fórmula flujo uniforme (por ejemplo de Manning) para la ecuación de movimiento, la Ec. 4.22. En esencia, se dice que, en lo que se refiere a momento, el flujo es constante. La inestabilidad de los fenómenos, sin embargo, se conserva a través de la ecuación de continuidad, Ec. 4-18 o la Ec. 4-21. La implicación de la suposición de onda cinemática es que el flujo inestable puede ser visualizado como una sucesión de flujos uniformes estables, con la pendiente de la superficie del agua que permanece constante en todo momento. Esto, por supuesto, se puede conciliar con la realidad sólo si la inestabilidad de flujo es muy suave; es decir, si los cambios en la etapa ocurren muy gradualmente.
In practice, a necessary condition for the applicability of Eq. 4-42 to unsteady flows is that the changes in momentum be negligible compared to the force driving the steady flow, i.e., gravity (the plane or channel slope). The kinematic flow number used in overland flow applications (Eq. 4-56) serves as a quantitative measure of how kinematic a given unsteady flow condition is; that is, of the extent to which Eq. 4-42 a good surrogate of Eq. 4-22 and, therefore, a valid description of the unsteady flow phenomena.
En la práctica, una condición necesaria para la aplicabilidad de la Ec. 4-42 a los flujos inestables es que los cambios en el momento son insignificantes en comparación con la fuerza impulsora del flujo constante, es decir, la gravedad (el plano o la pendiente del canal). El número de flujo cinemático utilizado en aplicaciones de flujo superficial (Ec. 4-56) sirve como una medida cuantitativa de cómo la cinemática una condición de flujo inestable dada es; es decir, de la medida en que la Ec. 4-42 un buen sustituto de la Ec. 4-22 y, por lo tanto, una descripción válida de los fenómenos de flujo no estacionario.
Kinematic wave solution. The application of kinematic wave theory to the overland flow problem begins with Eq. 4-18, repeated here for convenience:
Solución de la onda cinemática. La aplicación de la teoría de la onda cinemática al problema flujo superficial comienza con la Ec. 4-18, repetida aquí por conveniencia:
∂q ∂h
| ____ + ____ =
i ∂x ∂t | (4-18) |
Differentiating Eq. 4-42 with respect to flow depth, assuming that b and m are constants (a wide channel of constant friction) gives:
Diferenciando la Ec. 4-42 con respecto al flujo de profundidad, suponiendo que b y m son constantes (una amplio canal de fricción constante) da:
|
∂q q ____ = mbh m - 1 = m ( ____ ) = mu = c ∂h h | (4-43) |
in which c = celerity of a kinematic wave. Since in overland flow m > 1 (Table 4-3), the celerity of a kinematic wave is greater than the mean flow velocity.
en la que c = celeridad de una onda cinemática. Puesto que en el flujo superficial m > 1 (Tabla 4-3), la celeridad de una onda cinemática es mayor que la velocidad media del flujo.
Multiplying Eqs. 4-18 and 4-43 and using the chain rule,
Multiplicando las ecuaciones 4-18 y 4-43 y usando la regla de la cadena,
|
∂q ∂q ____ + c ____ = ci ∂t ∂x | (4-44) |
which is a form of the kinematic wave equation with q as the dependent variable.
que es una forma de la ecuación de onda cinemática con q como la variable dependiente.
Using the same approach, an expression for kinematic flow in terms of flow depth can be derived:
Utilizando el mismo enfoque, una expresión para el flujo cinemático en términos de profundidad de flujo se puede derivar:
|
∂h ∂h ____ + c ____ = i ∂t ∂x | (4-45) |
With c = dx/dt, i.e., the slope of the characteristic lines on an x-t plane (Fig. 4-16), the left side of
Con c = dx/dt, es decir, la pendiente de las líneas características en un plano x-t (Fig. 4-16), el lado izquierdo de las
|
dq ____ = ci dt | (4-46) |
|
dq ____ = i dx | (4-47) |
|
dh ____ = i dt | (4-48) |
|
dh i ____ = ____ dx c | (4-49) |
Figure 4-16 Characteristic lines on the x-t plane. / Líneas características en el plano x-t. |
In particular, Eq. 4-48 can be integrated to yield:
En particular, la Ec. 4-48 se pueden integrar para producir:
| h = i t | (4-50) |
which implies that the flow depth at any point along the plane increases linearly with time, provided that rainfall excess i remains constant.
que implica que la profundidad de flujo en cualquier punto a lo largo del plano aumenta linealmente con el tiempo, a condición de que el exceso de precipitaciones i permanece constante.
The overland flow solution under the kinematic wave assumption resembles that of the storage concept, with a rising limb, an equilibrium state, and a receding limb. Although the equilibrium flow is the same (qe = i L), the time to equilibrium is notably different, as is the shape of rising and receding limbs.
La solución de flujo superficial bajo la suposición de onda cinemática se asemeja a la del concepto de almacenamiento, con una curva ascendente, un estado de equilibrio, y una curva de retroceso. Aunque el flujo de equilibrio es el mismo (qe = i L), el tiempo para el equilibrio es notablemente diferente, como lo es la forma de las curvas ascendentes y de retroceso.
To derive the kinematic wave solution, Eq. 4-42 is expressed in terms of equilibrium outflow:
Para derivar la solución de onda cinemática, la Ec. 4-42 se expresa en términos del flujo de salida de equilibrio:
| qe = b hem | (4-51) |
in which, unlike in Eqs. 4-24 and 4-25, he is now interpreted as the equilibrium flow depth at the catchment outlet. Dividing Eq. 4-42 by Eq. 4-50 leads to:
en el que, a diferencia de las ecuaciones 4-24 y 4-25, he es ahora interpretada como la profundidad de flujo de equilibrio en la toma de captación. Dividiendo la Ec. 4-42 por la Ec. 4-50 conduce a:
|
q h m ___ = ( ___ ) qe he | (4-52) |
Since h = it (Eq. 4-50), this leads to:
Dado h = it (Ec. 4-50), esto conduce a:
|
q t m ___ = ( ___ ) qe tk | (4-53) |
in which tk = kinematic time parameter, defined as:
en el que tk = parámetro de tiempo cinemático, definido como:
|
he tk = _____ i | (4-54) |
Equation 4-53 is applicable for t ≤ tk. Otherwise, the flow would exceed the equilibrium value, which is clearly a physical impossibility. Thus, the kinematic time parameter may be interpreted as a kinematic time-to-equilibrium.
La ecuación 4-53 es aplicable para t ≤ tk. De lo contrario, el flujo excedería el valor de equilibrio, que es claramente una imposibilidad física. Por lo tanto, el parámetro de tiempo cinemático puede ser interpretado como un tiempo de equilibrio cinemático.
With Eq. 4-51, and since qe = iL and b = (1/n) So1/2 (for turbulent Manning friction in wide channels), the kinematic time parameter may be expressed as follows:
Con la Ec. 4-51, y desde qe = iL and b = (1/n) So1/2 (para la fricción de Manning turbulento en canales anchos), el parámetro de tiempo cinemático se puede expresar como sigue:
|
(nL) 1/m tk = ___________________ i (m - 1)/m So 1/(2m) | (4-55) |
which is the same as Eq. 4-29, albeit without the factor 2. In other words, the analytical solution to the kinematic wave equation is a parabola (Eq. 4-53), whereas the analytical solution of the storage concept is a hyperbolic trigonometric function (see, for instance, Eq. 4-38, applicable for m = 2).
que es la misma que la ecuació 4-29, aunque sin el factor de 2. En otras palabras, la solución analítica para la ecuación de la onda cinemática es una parábola (Ec. 4-53), mientras que la solución analítica del concepto de almacenamiento es una función trigonométrica hiperbólica (véase, por ejemplo, la Ec. 4-38, aplicable para m = 2).
Wooding's open book. The kinematic approach to the solution of the overland flow problem was studied in detail by Iwagaki [12], Henderson and Wooding [8], Wooding [29, 30, 31], and Woolhiser and Liggett [32], among others. Wooding developed the concept of the open book shown in Fig. 4-17, which has been extensively used in catchment modeling (Chapter 10). The open book is formed by two overland flow planes; the outflow from the planes is lateral inflow to the channel, which conveys the flow to the catchment outlet.
Libro abierto de Wooding. El enfoque cinemático a la solución del problema del flujo superficial se estudió en detalle por Iwagaki [12], Henderson y Wooding [8], Wooding [29, 30, 31], y Woolhiser y Liggett [32], entre otros. Wooding desarrolló el concepto del libro abierto se muestra en la Fig. 4-17, que ha sido utilizado ampliamente en el modelado de cuencas de captación (Capítulo 10). El libro abierto está formado por dos planos de flujo superficial; el flujo de salida de los planos es el flujo de entrada lateral para el canal, que transmite el flujo a la salida de captación.
Figure 4-17 Esquema de un libro abierto de captación de Wooding. [27]. |
Applicability of kinematic waves. Woolhiser and Liggett calculated the shape of the rising hydrograph under kinematic flow. Furthermore, they established the limit for the applicability of the kinematic wave in terms of the kinematic flow number, defined as follows:
Aplicabilidad de las ondas cinemáticas. Woolhiser y Liggett calcularon la forma del aumento del hidrograma bajo el flujo cinemático. Además, se estableció el límite para la aplicabilidad de la onda cinemática en términos del número de flujo cinemático, definido como sigue:
|
So L K = __________ F 2 ho | (4-56) |
in which K = kinematic flow number, a dimensionless number; F = Froude number corresponding to the equilibrium flow at the outlet; and ho = equilibrium flow depth at the outlet (i.e., he). Values of K greater than 20 describe kinematic flow, while lower values do not [18]. In other words, for low K values, Eq. 4-41 is no longer a good approximation of Eq. 4-22.
en el que el número K = número del flujo cinemático, un número adimensional; F = número de Froude correspondiente al flujo de equilibrio en la salida; y ho = profundidad de flujo de equilibrio en la salida (es decir, he). Los valores de K mayores que 20 describen el flujo de cinemático, mientras que los valores más bajos no lo hacen[18]. En otras palabras, para valores bajos de K, la Ec. 4-41 ya no es una buena aproximación de la Ec. 4.22.
In particular, since So is likely to vary within a wider range than either L, F, or ho, Eq. 4-56 could be interpreted to mean that the property of a wave being kinematic is directly related to plane slope: the steeper the slope, the greater the K value and the more kinematic the resulting flow should be. Conversely, the milder the slope, the lower the K value and the less kinematic the flow. The reason for this inability of the kinematic wave to account for a wide range of slopes is apparent from the nature of Eq. 4-22. The kinematic wave accounts only for friction and plane slopes. All other terms are excluded from the formulation and are, therefore, absent from the solution. For very mild plane slopes, the importance of these terms may be promoted to the point where neglecting them is no longer justified.
En particular, puesto que So es probable que varíe dentro de un rango más amplio que cualquiera de L, F, or ho, la Ec. 4-56 podría interpretarse en el sentido de que la propiedad de una onda siendo cinemática está directamente relacionada con la pendiente del plano: cuanto más pronunciada es la pendiente, mayor será el valor K y más cinemático el flujo resultante debe ser. A la inversa, cuanto más suave la pendiente, menor será el valor K y menos cinemático será el flujo. La razón de esta incapacidad de la onda cinemática a la cuenta para una amplia variedad de pendientes es evidente a partir de la naturaleza de la Ec. 4.22. La onda cinemática explica sólo para las pendientes de fricción y planas. Todos los demás términos son excluidos de la formulación y son, por lo tanto, ausentes de la solución. Para pendientes planas muy leves, la importancia de estos términos puede ser promovidos a tal punto que descuidarlos ya no se justifica.
While this appears to impose stringent limitations, the situation in practice is quite different. Most overland flow problems have steep slopes, on the order of So = 0.01 or more, resulting in the flow being essentially kinematic, as confirmed by their kinematic flow number (Eq. 4-56). However, much milder slopes, less than So = 0.001, result in very low kinematic flow numbers; for these cases, the kinematic wave solution may not be justified.
Si bien esto parece imponer limitaciones estrictas, la situación en la práctica es muy diferente. La mayoría de los problemas de flujo superficial tienen pendientes pronunciadas, del orden de So = 0.01 o más, lo que resulta en el flujo esencialmente cinemático, como lo confirma su número de flujo cinemático (Ec. 4-56). Sin embargo, las pistas mucho más suaves, menos de So = 0.001, dan lugar a números de flujo cinemáticos muy bajos; para estos casos, la solución de onda cinemática no puede justificarse.
Kinematic shock.
A source of complexity in kinematic wave solutions arises from the fact that the wave celerity in
Choque cinemático.
Una fuente de complejidad en soluciones de onda cinemática surge del hecho de que la celeridad de la onda en la
"...While the shock wave phenomenon may arise under highly selective physical circumstances, it is looked upon in this study as a property of the mathematical equations used to explore the overland flow problem rather than an observable feature of this hydrodynamic process."
"...Si bien el fenómeno de ondas de choque puede surgir en circunstancias físicas altamente selectivos, que es visto en este estudio como una propiedad de las ecuaciones matemáticas que se utilizan para explorar el problema de flujo superficial en lugar de una característica observable de este proceso hidrodinámico."
In nature, small amounts of diffusion and other irregularities usually act in such a way as to control and arrest shock development. An analytical solution, however, has no such imperfections. In essence, the total absence of diffusion in the analytical solution permits the uncontrolled development of the kinematic shock. Numerical solutions, however, usually have small amounts of diffusion and are, therefore, not perfect, with the shock being a rare occurrence in this case. This fact gives rise to practical implications for stream channel and catchment routing (Chapters 9 and 10).
En la naturaleza, las pequeñas cantidades de difusión y otras irregularidades suelen actuar de una manera tal como para controlar y detener el desarrollo de shock. Una solución analítica, sin embargo, no tiene esas imperfecciones. En esencia, la ausencia total de difusión en la solución analítica permite el desarrollo incontrolado de la cinemática de choque. Las soluciones numéricas, sin embargo, por lo general tienen pequeñas cantidades de difusión y son, por lo tanto, no perfectas, con ser el choque un hecho poco habitual en este caso. Este hecho da lugar a consecuencias prácticas para canal de flujo y el enrutamiento de captación (Capítulos 9 y 10).
Comparison of storage and kinematic wave solutions. Figure 4-18 shows dimensionless rising hydrographs of storage-concept overland flow solutions for values of 1 ≤ m ≤ 3. Note that dimensionless discharge is defined as: q* = q /qe, and dimensionless time as: t* = t /te. For comparison, the rising hydrograph of the kinematic wave (KW) is also shown in Fig. 4-18. This figure clearly shows that the response of the kinematic wave solution is about twice as fast as that of the storage concept (compare Eq. 4-29 for the storage concept with Eq. 4-54 for the kinematic wave).
Comparativa de almacenamiento y soluciones de onda cinemática. Figura 4-18 muestra hidrogramas crecientes adimensionales de soluciones de flujo superficial de almacenamiento de concepto para valores de 1 ≤ m ≤ 3. Tenga en cuenta que la descarga adimensional se define como: q* = q /qe, y tiempo adimensional como: t* = t /te. Para la comparación, el aumento del hidrograma de la onda cinemática (KW) también se muestra en la Fig. 4-18. Esta figura muestra claramente que la respuesta de la solución de onda cinemática es aproximadamente dos veces más rápido que el del concepto de almacenamiento (comparar la Ec. 4-29 para el concepto de almacenamiento con la Ec. 4-54 para la onda cinemática).
Figure 4-18 Dimensionless rising hydrographs of overland flow using the storage concept [24]. / Figura 4-18 Hidrogramas crecientes adimensionales de flujo superficial utilizando el concepto de almacenamiento [24]. |
Figure 4-19 shows dimensionless receding hydrographs of storage-concept overland flow solutions for values of 1 ≤ m ≤ 3.
La Figura 4-19 muestra hidrogramas retroceso adimensionales de soluciones de flujo superficial de almacenamiento concepto para los valores de 1 ≤ m ≤ 3.
Figure 4-19 Dimensionless receding hydrographs of overland flow [24]. / Hidrogramas retroceso adimensionales de flujo superficial [24]. |
Overland Flow Solution Based on Diffusion Wave Theory / Solución del Flujo Superficial Basado en la Teoría de Onda de Difusión
According to diffusion wave theory, the flow depth gradient ∂h/∂x in Eq. 4-22 is largely responsible for the diffusion mechanism, which is naturally present in unsteady free surface flows. Therefore, its inclusion in the analysis should provide runoff concentration with diffusion.
Según la teoría de onda de difusión, el gradiente de profundidad de flujo ∂h/∂x en la Ec. 4-22 es en gran parte responsable del mecanismo de difusión, que está naturalmente presente en los flujos de superficie libre inestables. Por lo tanto, su inclusión en el análisis debe proporcionar concentración de escorrentí con la difusión.
The inclusion of the depth gradient term substantially increases the difficulty of obtaining a solution. An established procedure is to linearize the governing equations, Eqs. 4-21 and 4-22, around reference flow values. This entails using small-perturbation theory to develop linear analogs of these equations. This procedure, while heuristic, has worked well in a number of applications.
La inclusión del término gradiente de profundidad aumenta sustancialmente la dificultad de obtener una solución. Un procedimiento establecido es para linealizar las ecuaciones que gobiernan, las ecuaciones 4-21 y 4-22, en torno a los valores de flujo de referencia. Esto implica el uso de la teoría de pequeña perturbación para desarrollar análogos lineales de estas ecuaciones. Este procedimiento, mientras heurístico, ha funcionado bien en una serie de aplicaciones.
Following Lighthill and Whitham [17], the linear analogs of Eqs. 4-21 and 4-22, neglecting the inertia terms (the first two terms of Eq. 4-22) and the momentum source term for simplicity, are, respectively,
Siguiendo Lighthill y Whitham [17], los análogos lineales de ecuaciones 4-21 y 4-22, dejando de lado los términos de inercia (los dos primeros t&eacue;rminos de la Ec. 4-22) y el término fuente de momento para la simplicidad, son, respectivamente,
|
∂h ∂h ∂u ___ + uo ___ + ho ___ = i ∂t ∂x ∂x | (4-57) |
|
∂h u 4 h ___ + So [ 2 (___) - (__)(___) ] = 0 ∂x uo 3 ho | (4-58) |
The coefficients of Eq 4-57 are constant, being the reference flow velocity uo and depth ho, respectively. The second term of Eq. 4-58 represents a combined linear version of the friction slope Sf and channel slope So. Furthermore, in Eq. 4-58 friction is described by the Manning formula. If the Chezy formula is used, the factor 4/3 is replaced by 1.
Los coeficientes de la Ec. 4-57 son constantes, siendo la referencia la velocidad de flujo uo y profundidad ho, respectivamente. El segundo término de la Ec. 4-58 representa una versión lineal combinada de la pendiente de fricción Sf y la pendiente del canal So. Además, en la Ec. 4-58 de fricción se describe por la fórmula de Manning. Si la fórmula de Chezy se usa, el factor 4/3 se sustituye por 1.
Differentiating Eq. 4-58 with respect to space and eliminating the term ∂u/∂x from the resulting equation (with the aid of Eq. 4-57), the following is obtained:
Diferenciando la Ec. 4-58 con respecto al espacio y eliminando el término ∂u/∂x apartir de la ecuación resultante (con la ayuda de la Ec. 4-57), se obtiene la siguiente:
|
∂h 5 ∂h uo ho ∂ 2h ___ + (___) uo ____ = i + (________) ______ ∂t 3 ∂x 2So ∂x 2 | (4-59) |
A similar expression with discharge as dependent variable may also be derived, albeit at the cost of increased algebraic manipulation (Chapter 9).
Una expresión similar con descarga como variable dependiente puede derivarse también, aunque a costa de una mayor manipulación algebraica (Capítulo 9).
Unlike the kinematic wave equation (Eq. 4-44), which has no second-order term, the diffusion wave equation (Eq. 4-59) has a second-order term. Therefore, the latter can describe not only runoff concentration but also diffusion. Equation 4-59 can be expressed in the following form:
A diferencia de la ecuación de onda cinemática (Ec. 4-44), que no tiene término de segundo orden, la ecuación de onda de difusión (Ec. 4-59) tiene un término de segundo orden. Por lo tanto, este último se puede describir no sólo la concentración de escorrentía sino también la difusión. La ecuación 4-59 se puede expresar de la siguiente forma:
|
∂h ∂h ∂ 2h ___ + c ___ = i + νh ______ ∂t ∂x ∂x 2 | (4-60) |
in which
en el cual
| c = (5/3) uo | (4-61) |
is the celerity of a diffusion wave, for turbulent Manning friction in hydraulically wide channels (overland flow), and
es la celeridad de una ola de difusión, por la fricción de Manning turbulento en canales anchos hidráulicamente (flujo superficial), y
|
uo ho νh = ________ 2So | (4-62) |
is the hydraulic diffusivity, or channel diffusivity.
es la difusividad hidráulica, o difusividad del canal.
Equation 4-59 implies that the diffusion component (second-order term) is small compared with the concentration component (first-order terms) and that the channel diffusivity controls the diffusion contribution to the flow. In effect, for very low values of So, channel diffusivity is very large. In the limit, as channel slope approaches zero, channel diffusivity grows unbounded and Eq. 4-59 is no longer applicable. However, for realistic mild slopes (approximately in the range 0.001-0.0001), the contribution of the diffusion term can be quite significant. Diffusion wave theory, then, applies for the milder slopes for which kinematic wave theory is not sufficient. Its application to catchment routing and hydrologic models of overland flow is discussed in Chapter 10.
La ecuación 4-59 implica que el componente de difusión (término de segundo orden) es pequeño en comparación con el componente de la concentración (términos de primer orden) y que la difusividad del canal controla la contribución de difusión para el flujo. En efecto, para valores muy bajos de So, la difusividad del canal es muy grande. En el límite, como canal de pendiente se aproxima a cero, la difusividad del canal crece sin límites y la Ec. 4-59 ya no es aplicable. Sin embargo, para pendientes suaves realistas (aproximadamente en el rango de 0.001 - 0-0001), la contribución del término de difusión puede ser muy significativo. La teoría de la onda de difusión, a continuación, se aplica a las pendientes más suaves para los que la teoría de la onda cinemática no es suficiente. Su aplicación al enrutamiento de captación y modelos hidrológicos de flujo superficial se discute en el Capítulo 10.
In summary, overland flow techniques can provide more detail than the rational method in describing the peak and timing of outflow hydrographs from small catchments. The increase in detail, however, is invariably associated with greater complexity. In practice, it is reckoned that rainfall and abstraction modules must be coupled with the overland flow module in order to arrive at a meaningful model. Ideally, these modules should be as detailed as the overland flow module. However, due to the complex spatial and temporal variability of rainfall and hydrologic abstractions, this consistency between model components is not always possible (Fig. 4-20).
En resumen, las técnicas de flujo superficial pueden proporcionar más detalle que el método racional para describir el pico y el momento de hidrogramas de salida de flujo desde pequeñas cuencas. El aumento en detalle, sin embargo, se asocia invariablemente con mayor complejidad. En la práctica, se calcula que los módulos de las precipitaciones y de extracción deben acoplarse con el módulo de flujo superficial con el fin de llegar a un modelo significativo. Idealmente, estos módulos deben ser tan detallado como el módulo de flujo superficial. Sin embargo, debido a la variabilidad espacial compleja y temporal de las precipitaciones y abstracciones hidrológicas abstracciones, esta coherencia entre los componentes del modelo no siempre es posible (Fig. 4-20).
Figure 4-20 Rural watershed showing the spatial variability of infiltration. / Cuenca rural mostrando la variabilidad espacial de la infiltración. |
PREGUNTAS
|
|
Name three properties that characterize a small catchment. Explain each one of them.
Nombre tres propiedades que caracterizan a una pequeña cuenca. Explicar cada uno de ellos.
What hydrologic processes does the rational method account for? Explain how they affect runoff.
¿Qué procesos hidrológicos representa el método racional? Explicar cómo afectan a la escorrentía.
What processes are not considered in the rational method? Explain.
¿Qué procesos no está considerados en el método racional? Explicar.
How are the frequencies of storms and floods related? How does the rational method account for this difference?
¿Cómo son las frecuencias de las tormentas e inundaciones relacionadas? ¿Cómo explica el método racional para esta diferencia?
What processes are included in the runoff coefficient?
¿Qué procesos están incluidos en el coeficiente de escorrentía?
Under what assumption does the rational method provide the shape of the outflow hydrograph?
Bajo qué hipótesis el método racional proporciona la forma del hidrograma de salida?
Describe the phenomenon of overland flow. Contrast overland flow analysis with the rational method approach.
Describir el fenómeno de flujo superficial. Análisis de flujo superficial contrasta con el enfoque del método racional.
What crucial assumption makes the storage solution of overland flow different from the kinematic wave solution?
¿Qué suposición fundamental hace que la solución de almacenamiento de flujo superficial sea diferente de la solución de onda cinemática?
Why is overland flow likely to be of mixed laminar-turbulent nature? How is this modeled in practice?
¿Por qué es probable que el flujo superficial sea de carácter mixto laminar turbulento? ¿Cómo se modela en la práctica?
What is the difference between the time of concentation (or time to equilibrium) in storage-concept and kinematic-wave overland flow models?
¿Cuál es la diferencia entre el tiempo de concentración (o tiempo de equilibrio) en modelos de flujo superficial de onda cinemática y de almacenamiento-concepto?
What is an ideal reservoir? An ideal channel? Contrast these two concepts.
¿Qué es un reservorio ideal? Un canal ideal? Contrastar estos dos conceptos.
What is the kinematic wave celerity? Why is it generally greater than the flow velocity?
¿Cuál es la celeridad de la onda cinemática? ¿Por qué es generalmente mayor que la velocidad de flujo?
What is the kinematic flow number? What does it describe? For what kind of channel slope is it likely that the kinematic wave solution would not be applicable?
¿Cuál es el número de flujo cinemático? ¿Qué se describe? ¿Para qué tipo de pendiente de canal es probable que la solución de onda cinemática no fuera aplicable?
What is kinematic shock? Why does it often occur in analytic kinematic wave solutions while it is seldom present in numerical solutions?
¿Qué es el choque cinemático? ¿Por qué a menudo se producen en las soluciones de onda cinem&aacue;ticas analíticas mientras que es rara vez que se presente en las soluciones numéricas?
Contrast kinematic and diffusion wave approaches to overland flow.
El contraste cinemático y la onda de difusión se acerca al flujo superficial.
Why does Eq. 4-59 describe runoff diffusion, while Eq. 4-43 does not?
¿Por qué la Ec. 4-59 describe la difusión de escurrimiento, mientras que la Ec. 4-43 no lo hace?
What is hydraulic diffusivity?
¿Qué es la difusividad hidráulica?
PROBLEMAS
|
|
Rain falls on a 150-ha catchment with intensity 2 cm/h and duration 2 h. Use the rational method to calculate the peak runoff, assuming runoff coefficient C = 0.6 and time of concentration
tc = 1.5 h. La lluvia cae en una cuenca de 150 hectáreas con una intensidad de 2 cm / h y la duración de 2 h. Utilizar el método racional para calcular la escorrentía pico, asumiendo el coeficiente de escorrentía C = 0.6 y el tiempo de concentración
tc = 1.5 h. Rain falls on a 300-ac watershed with intensity 0.5 in./h and duration 2 h. Use the rational method to calculate the peak runoff, assuming runoff coefficient C = 0.4 and time of concentration tc = 2 h.
La lluvia cae en una cuenca de 300 ac con una intensidad de 0.5 in./h y la duración de 2 h. Utilizar el método racional para calcular la escorrentía pico, asumiendo el coeficiente escorrentía C = 0.4 y tiempo de concentración tc = 2 h.
Rain falls on a 545-ha catchment with intensity 45 mm/h and duration 1 h. Use the rational method to calculate the peak runoff for the following conditions:
La lluvia cae en una cuenca de 545 ha con una intensidad de 45 mm / h y la duración de 1 h. Utilizar el método racional para calcular la escorrentía pico para las siguientes condiciones:
- Natural, with time of concentration 2 h and C = 0.4;
Natural, con el tiempo de concentración de 2 h y C = 0.4;
- Improved, partially paved area, with time of concentration tc = 1 h and C = 0.7.
Mejorado, área parcialmente pavimentada, con tiempo de concentración tc = 1 h y C = 0.7.
State any assumptions used.
Indicar la existencia de los supuestos utilizados.
- Natural, with time of concentration 2 h and C = 0.4;
Rain falls on a 1.5-km2 watershed with intensity 20 mm/h and duration 2 h. Use the rational method to calculate the peak runoff for the following two conditions:
La lluvia cae en una cuenca de 1.5-km2 con una intensidad de 20 mm / h y la duración de 2 h. Utilizar el método racional para calcular la escorrentía pico para las dos condiciones siguientes:
- Vegetated (natural) watershed with time of concentration tc = 3 h and C = 0.3; and
Cuencas (natural) con vegetación con tiempo de concentración tc = 3 h y C = 0.3; y
- Improved, partially paved area with time of concentration tc = 2 h and C = 0.6.
Mejorada, área parcialmente pavimentada con tiempo de concentración tc = 2 h and C = 0.6.
State any assumptions used.
Indicar la existencia de los supuestos utilizados.
- Vegetated (natural) watershed with time of concentration tc = 3 h and C = 0.3; and
Rain falls on a catchment with intensity 35 mm/h and duration 2 h. The catchment area is 250 ha, with time of concentration tc = 2 hand φ = 15 mm/h. Calculate the peak runoff. State any assumptions used.
La lluvia cae en una cuenca con una intensidad de 35 mm / h y la duración de 2 h. El área de influencia es de 250 ha, con tiempo de concentración tc = 2 hand φ = 15 mm/h. Calcular la escorrentía máxima. Indicar la existencia de los supuestos utilizados.
Rain falls on a watershed with intensity 1 in./h and duration 3 h. The watershed area is 500 ac, with time of concentration tc = 2 h and φ = 0.3 in./h. Calculate the peak runoff. State any assumptions used.
La lluvia cae en una cuenca con una intensidad de 1 in./h y la duración de 3 h. El área de la cuenca es de 500 ac, con tiempo de concentración tc = 2 h and φ = 0.3 in./h. Calcular la escorrentía máxima. Indicar la existencia de los supuestos utilizados.
Rain falls on a watershed with intensity 30 mm/h and duration 1 h. The watershed area is 0.8 km2 with time of concentration tc = 2 h and φ = 15 mm/h. Use the rational method to calculate the peak runoff. State any assumptions used.
La lluvia cae en una cuenca con una intensidad de 30 mm / h y la duración de 1 h. El área de la cuenca es de km2 con tiempo de concentración tc = 2 h and φ = 15 mm/h. Utilizar el método racional para calcular la escorrentía máxima. Indicar la existencia de los supuestos utilizados.
Rain falls on a 125-ha catchment with the following characteristics:
La lluvia cae en una cuenca de 125 ha con las siguientes características:
- 20%, C = 0.3;
- 30%, C = 0.4;
- 50%, C = 0.6.
Calculate the peak runoff due to a storm of 45 mm/h intensity lasting 1 h. Assume time of concentration tc = 30 min.
Calcular la escorrentía máxima debido a una tormenta de 45 mm / h de intensidad que dura 1 h. Supongamos tiempo de concentración es de tc = 30 min.
Rain falls on a 90-ha catchment with the following characteristics:
La lluvia cae en una cuenca de 90 ha con las siguientes características:
- 12 ha, C = 0.3;
- 48 ha, C = 0.7;
- 30 ha, C = 0.9.
Calculate the peak runoff from a 50 mm/h storm lasting 2 h. Assume time of concentration tc = 2 h.
Calcular el escurrimiento máximo de un tormenta de 50 mm / h que dura 2 h. Supongamos el tiempo de concentración tc = 2 h.
Rain falls on a 300-ha composite catchment which drains two subareas, as follows:
La lluvia cae en una cuenca compuesta de 300 ha que drena dos subáreas, de la siguiente manera:
- Subarea A, steep, draining 20%, with time of concentration 10 min and C = 0.8; and
Subárea A, empinada, el drenaje de 20%, con el tiempo de concentración de 10 min y C = 0.8; y
- Subarea B, milder steep, draining 80%, with time of concentration 60 min and C= 0.4.
Subárea B, empinada más suave, el drenaje de 80%, con el tiempo de la concentración de 60 min y C= 0.4.
Calculate the peak runoff corresponding to the 25-y-frequency. Use the following IDF function:
Calcular la escorrentía máxima correspondiente a la frecuencia 25-y. Utilizar la siguiente función de IDF:
800T 0.2
I = ______________
(tr + 15) 0.7in which I = rainfall intensity in millimeters per hour, T = return period in years, and tr = rainfall duration in minutes. Assume linear flow concentration at the catchment outlet.
en la que I = intensidad de la lluvia en milímetros por hora, T = período de retorno en años, y tr = duración de precipitaciones en minutos. Asumir la concentración de flujo lineal en la salida de la cuenca.
- Subarea A, steep, draining 20%, with time of concentration 10 min and C = 0.8; and
- Rain falls on a 150-ha composite catchment, which drains two subareas, as follows:
La lluvia cae en una cuenca compuesta de 150 ha, que drena dos subáreas, de la siguiente manera:
- Subarea A, steep, draining 30%, with time of concentration 20 min; and
Subárea A, empinada, el drenaje de 30%, con el tiempo de la concentración de 20 min; y
- Subarea B, milder steep, draining 70%, with time of concentration 60 min.
Subárea B, empinada más leve, el drenaje de 70%, con el tiempo de la concentración de 60 min.
The hydrologic abstraction is given in terms of φ = 25 mm/h. Calculate the 100-y-frequency peak flow. Use the following IDF function:
La abstracción hidrológica se da en términos de φ = 25 mm/h.. Calcular el flujo máximo de 100-y-frecuencia. Utilizar la siguiente función de IDF:
650T 0.22
I = _______________
(tr + 18) 0.75in which I = rainfall intensity in millimeters per hour, T = return period in years, and tr = rainfall duration in minutes. Assume linear flow concentration at the catchment outlet. State any other assumptions used.
en la que I = intensidad de la lluvia en milímetros por hora, T = período de retorno en años, y tr = duración de precipitaciones en minutos. Asumir la concentración de flujo lineal en la salida de la cuenca. Indicar la existencia de otros supuestos utilizados.
- Subarea A, steep, draining 30%, with time of concentration 20 min; and
Rain falls on a composite catchment, which drains two subareas, as follows:
La lluvia cae en una cuenca compuesta, que drena dos subáreas, de la siguiente manera:
- Subarea A, draining 84 ha, C = 0.4, time of concentration 30 min;
Subárea A, drenaje de 84 ha, C = 0.4, el tiempo de la concentración de 30 min;
- Subarea B, draining 180 ha, C = 0.6, time of concentration 60 min.
Subárea B, drenaje de 180 ha, C = 0.6, tiempo de concentración de 60 min.
The runoff concentration for subarea B is a nonlinear function expressed as follows:
La concentración de la escorrentía para la subárea B es una función no lineal expresa como sigue:
% of time
of concentration / % de tiempo de concentración0 10 20 30 40 50 60 70 80 90 100 % of maximum
discharge / % de descarga máxima descarga0 5 10 20 30 50 70 80 90 95 100 Calculate the 50-yr-frequency peak flow. Use the following IDF function:
Calcular el flujo máximo de 50-yr-frecuencia. Utilizar la siguiente función de IDF:
52T 0.24
I = ______________
(tr + 22) 0.8in which I = rainfall intensity in millimeters per hour, T = return period in years, and tr = rainfall duration in minutes.
en la que I = intensidad de la lluvia en milímetros por hora, T = período de retorno en años, y tr = duración de precipitaciones en minutos.
- Subarea A, draining 84 ha, C = 0.4, time of concentration 30 min;
A developed catchment is divided into five subareas, as sketched in Fig. 4-10, with the following data:
Una cuenca desarrollada se divide en cinco subáreas, como esquema en la Fig. 4-10, con los siguientes datos:
Collection Point / Punto de Colección Subarea Increment / Incremento Subárea
(ha)Travel Time / Tiempo de viaje
(min)C A 25 10 0.6 B 40 15 0.6 C 60 20 0.5 D 50 25 0.5 E 25 20 0.4 Calculate the 10-y-frequency peak flow. Use the following IDF function:
Calcular el flujo máximo de 10-y-frecuencia. Utilizar la siguiente función de IDF:
500T 0.18
I = _______________
(tr + 20) 0.78in which I = rainfall intensity in millimeters per hour, T = return period in years, and tr = rainfall duration in minutes.
en la que I = intensidad de la lluvia en milímetros por hora, T = período de retorno en años, y tr = duración de precipitaciones en minutos.
A developed catchment is divided into five subareas, as sketched in Fig. 4-10, with the following data:
Una cuenca desarrollada se divide en cinco subáreas, como esquema en la Fig. 4-10 con los siguientes datos:
Collection Point / Punto de Colección Subarea Increment / Incremento de Subárea
(ha)Travel Time / Tiempo de viaje
(min)C A 15 5 0.7 B 30 10 0.6 C 20 15 0.4 D 10 15 0.7 E 15 15 0.9 Calculate the 10-y-frequency peak flow. Use the following IDF function:
Calcular el flujo máximo de 10-y-frecuencia. Utilizar la siguiente función de IDF:
750T 0.2
I = ______________
( tr + 25) 0.7in which I = rainfall intensity in millimeters per hour, T = return period in years, and tr = rainfall duration in minutes.
en la que I = intensidad de la lluvia en milímetros por hora, T = período de retorno en años, y tr = duración de precipitaciones en minutos.
The length of an overland flow plane is L = 90 m. Determine the equilibrium outflow corresponding to a rainfall excess i = 35 mm/h.
La longitud de un plano de flujo superficial es L = 90 m. Determinar el flujo de salida de equilibrio que corresponde a un exceso de lluvia i = 35 mm/h.
An overland flow plane is 100 m long and 200 m wide, with time to equilibrium equal to 1 h. Estimate the equilibrium storage volume (in cubic meters) for a rainfall excess i = 54 mm/h.
Un plano de flujo superficial es de 100 m de largo y 200 m de ancho, con el tiempo al equilibrio igual a 1 h. Estimar el volumen de almacenamiento de equilibrio (en metros cúbicos) por un exceso de lluvia i = 54 mm/h.
Use the storage concept to calculate the time to equilibrium for an overland flow plane with the following characteristics: 100% laminar flow, plane length L = 75 m, plane slope So = 0.01, rainfall excess i = 72 mm/h, water temperature 20°C.
Utilizar el concepto de almacenamiento para calcular el tiempo hasta el equilibrio para un plano de flujo superficial con las siguientes características: 100% de flujo laminar, la longitud del plano L = 75 m, pendiente del plano So = 0.01, exceso de precipitaciones i = 72 mm/h, temperatura del agua de 20°C.
Calculate the mean overland flow depth (at equilibrium) under a laminar flow regime for a plane length L = 80 m, rainfall excess i = 30 mm/h, and plane slope So = 0.012. Use water temperature T = 15°C. What would be the mean overland flow depth if the water temperature increased to 25°C?
Calcular la profundidad de flujo superficial medio (en equilibrio) bajo un régimen de flujo laminar para una longitud plana L = 80 m, exceso de lluvia i = 30 mm/h, y la pendiente plana So = 0.012. Usar la temperatura del agua T = 15°C. ¿Cuál sería la profundidad de flujo superficial media si la temperatura del agua se incrementó a 25°C?
Use the storage concept to calculate the time to equilibrium for an overland flow plane with the following characteristics: turbulent Manning friction with n = 0.06, plane length L = 50 m, plane slope So = 0.02, rainfall excess i = 72 mm/h.
Utilizar el concepto de almacenamiento para calcular el tiempo hasta el equilibrio de un plano de flujo superficial con las siguientes características: la fricción de Manning turbulenta con n = 0.06, longitud del plano L = 50 m, pendiente del plano So = 0.02, exceso de precipitaciones i = 72 mm / h.
Calculate the rising limb of an overland flow hydrograph using Horton's equation (Eq. 4-37) assuming 75% turbulent flow. Use: Manning n = 0.06, plane length L = 60 m, plane slope So = 0.015, rainfall excess i = 30 mm/h.
Calcular la curva ascendente de un hidrograma de flujo superficial utilizando la ecuación de Horton (Ec. 4-37), suponiendo el 75% del flujo turbulento. Usar: Manning n = 0.06, la longitud del plano L = 60 m, pendiente del plano So = 0.015, exceso de precipitación i = 30 mm/h.
Calculate the rising limb of an overland flow hydrograph using Izzard's equation (Eq. 4-39). Use: L = 60 m, So = 0.015, i = 30 mm/h, and ν = 1 cs (water temperature T = 20°C).
Calcular la curva ascendente de un hidrograma de flujo superficial usando la ecuación de Izzard (Ec. 4-39). Usar: L = 60 m, So = 0.015, i = 30 mm/h, y ν = 1 cs (temperatura del agua T = 20°C).
Prove that Eqs. 4-37 and 4-38 are equivalent.
Demostrar que las ecuaciones 4-37 y 4-38 son equivalentes.
Calculate the receding limb of an overland flow hydrograph, using m = 3, L = 50 m, So = 0.02, i = 33 mm/h, and ν = 1 cs.
Calcular la curva descendente de un hidrograma de flujo superficial, usando m = 3, L = 50 m, So = 0.02, i = 33 mm/h, y ν = 1 cs.
Derive the formula for the kinematic time parameter for 100% laminar flow (m = 3).
Deducir la fórmula para el parámetro de tiempo cinemático para el 100 % de flujo laminar (m = 3).
Using the formula derived in Problem 4-24, calculate the rising limb of an overland flow hydrograph using the kinematic wave approach, assuming plane length L = 100 m, plane slope So = 0.01 , rainfall excess i = 25 mm/ h, and water temperature T = 20°C.
Utilizando la fórmula derivada en el Problema 4-24, calcular la curva ascendente de un hidrograma de flujo superficial utilizando el enfoque de onda cinemática, asumiendo la longitud del plano L = 100 m, pendiente del plano So = 0.01 , exceso de precipitación i = 25 mm/ h, y temperatura del agua T = 20°C.
An overland flow plane has the following characteristics: plane length L = 35 m, plane slope So = 0.008, Manning n = 0.08, rainfall excess i = 55 mm/ h. Determine if the kinematic wave approximation is applicable to this set of overland flow conditions.
Un plano de flujo superficial tiene las siguientes características: longitud del plano L = 35 m, pendiente del plano So = 0.008, Manning n = 0.08, exceso de precipitación i = 55 mm/ h. Determinar si la aproximación de la onda cinemática es aplicable a este conjunto de condiciones de flujo superficial.
Calculate the hydraulic (channel) diffusivity for each of the following two flow conditions:
Calcular la difusividad (canal) hidráulica para cada una de las dos condiciones de flujo siguientes:
Bed slope So = 0.005, mean flow depth ho = 0.01 m. and mean velocity uo = 0.05 m/ s; and
Pendiente del lecho So = 0.005, profundidad del flujo medio ho = 0.01 m. y la velocidad media uo = 0.05 m/ s; y
Bed slope So = 0.00005, mean flow depth ho = 0.02 m, and mean velocity uo = 0.1 m/ s.
Pendiente del lecho So = 0.00005, profundidad del flujo medio ho = 0.02 m, y velocidad media uo = 0.1 m/ s.
BIBLIOGRAFÍA
|
|
Agricultural Research Service. U.S. Department of Agriculture. (1973). "Linear Theory of Hydrologic Systems," Technical Bulletin No. 1468, (J. C. 1. Dooge, author). Washington, D.C.
American Society of Civil Engineers. (1960). "Design and Construction of Sanitary and Storm Sewers," Manual of Engineering Practice No. 37, also Water Pollution Control Federation Manual of Practice No. 9.
Chow, V. T. (1959). Open Channel Hydraulics. New York: McGraw-Hill.
Chow, V. T., and A. Ben-Zvi. (1973). "Hydrodynamic Modeling of Two-dimensional Watershed Flow," Journal of the Hydraulics Division, ASCE, Vol. 99, No. HYll, Nov. pp. 2023-2040.
County of Kern, California. (1985). "Revision of Coefficient of Runoff Charts," Office Memo, dated January 18, 1985.
County of Solano, California. (1977). "Hydrology and Drainage Design Procedure," prepared by Water Resources Engineers, Inc., Walnut Creek, California, October.
Hathaway, G. A. (1945). "Design of Drainage Facilities," in Military Airfields, A Symposium, Transactions, American Society of Civil Engineers. Vol. 110, pp. 697-733.
Henderson, F. M., and R. A. Wooding. (1964). "Overland Flow and Groundwater Flow from a Steady Rainfali of Finite Duration," Journal of Geophysical Research. Vol. 69, No.8, April, pp. 1531-1540.
Henderson, F. M. (1965). Open Channel Flow. New York: MacMillan.
Horton, R. E. (1938). "The Interpretation and Application of Runoff Plot Experiments with Reference to Soil Erosion Problems," Proceedings, Soil Science Society of America. Vol. 3, pp. 340-349.
Hydrologic Engineering Center, U.S. Army Corps of Engineers. (1998). "HEC-1, Flood Hydrograph Package, Users Manual," September 1981, revised January 1985, revised 1998.
Iwagaki, Y. (1955). "Fundamental Studies on the Runoff Analysis by Characteristics," Bulletin, Disaster Prevention Research Institute, Vol. 10, Kyoto University, December.
Izzard, C. F. (1944). "The Surface Profile of Overland Flow," Transactions. American Geophysical Union, Vol. 25, No.6, pp. 959-968.
Izzard, C. F. (1946). "Hydraulics of Runoff from Developed Surfaces," Proceedings. Highway Research Board, Washington, D.C., Vol. 26, pp. 129-146.
Kibler, D. F., and D. A. Woolhiser. (1970). "The kinematic cascade as a hydrologic model," Hydrology Paper No. 39, Colorado State University, Fort Collins, Colo., March.
Lai, C. (1986). "Numerical Modeling of Unsteady Qpen Channel Flow," in Advances in Hydroscience. Vol. 14. Orlando: Academic Press.
Lighthill. M. H., and G. B. Whitham. (1955). "On Kinematic Waves. 1. Flood Movement in Long Rivers," Proceedings, Royal Society. London, Vol. A229, May, pp. 281-316.
Mahmood, K., and Yevjevich, V. (1975). Unsteady Flow in Open Channels, in 3 volumes. Fort Collins, Colo.: Water Resources Publications.
Miller, W. A., and Cunge, J. A. (1975). "Simplified Equations of Unsteady Flow," in Unsteady Flow in Open Channels, K. Mahmood and V. Yevjevich, eds. , Fort Collins, Colo. : Water Resources Publications.
NOAA National Weather Service. (1973). Atlas 2: Precipitation Atlas of the Western United States.
NOAA National Weather Service. (1977). "Five- to 60-Minute Precipitation Frequency for the Eastern and Central United States," Technical Memorandum NWS HYDRO-35.
Ponce, V. M., and D. B. Simons. (1977). "Shallow Wave Propagation in Open Channel Flow," Journal of the Hydraulics Division, ASCE, Vol. 103, No. HY12, December, pp. 1461-1476.
Ponce, V. M. (1994). "New perspective on the convection-diffusion-dispersion equation," Water Resources Research, Vol. 30, No. 5, May, pp. 1619-1620.
Ponce, V. M., O. I. Cordero-Braña, and S. Y. Hasenin. (1997). "Generalized conceptual modeling of dimensionless overland flow hydrographs," Journal of Hydrology, 200, pp. 222-227.
Rantz, S. E. (1971). "Suggested Criteria for Hydrologic Design of Storm-drainage Facilities in the San Francisco Bay Region, California," U. S. Geological Survey Open-file Report, Menlo Park, California.
San Diego County. (1985). Hydrology Manual, San Diego, California, revised January.
Schaake, Jr., J. C., Geyer, and 1. W. Knapp. (1967). "Experimental Examination of the 'Rational Method," Journal of the Hydraulics Division, ASCE, Vol. 93, No. HY6, November, pp. 353-370.
Weather Bureau, U.S. Dept. of Commerce. (1963). "Rainfall Frequency Atlas of the United States for Durations from 30 Minutes to 24 Hours and Return Periods from 1 to 100 Years," Technical Paper No. 40.
Wooding, R. A. (1965) "A Hydraulic Model for the Catchment-stream Problem, I. Kinematic Wave Theory," Journal of Hydrology, Vol. 3, Nos. 3/4, pp. 254-267.
Wooding, R. A. (1965) "A Hydraulic Model for the Catchment-stream Problem, II. Numerical Solutions," Journal of Hydrology, Vol. 3, Nos. 3/4, pp. 268-282.
Wooding, R. A. (1965) "A Hydraulic Model for the Catchment-stream Problem, III. Comparison with Runoff Observations," Journal of Hydrology, Vol. 4, pp. 21-37.
Woolhiser, D. A., and Liggett, J. A. (1967). "Unsteady One-dimensional Flow Over a Plane: The Rising Hydrograph," Water Resources Research, Vol. 3, pp. 753-771.
| http://engineeringhydrology.sdsu.edu |
|
171204 23:00 |