|
|
|
CAPÍTULO 6: ANÁLISIS DE FRECUENCIA |
|
"If the sediment load in a stream is reduced, equilibrium can be restored if the water discharge
or the bottom slope are reduced, or if the sediment diameter increases the proper amount." Emory W. Lane (1955)
"Si se reduce la carga de sedimentos en una corriente, el equilibrio puede ser restaurado si la descarga de agua o la pendiente del fondo se reducen, o si el diámetro de sedimentos aumenta la cantidad adecuada.."
| Emory W. Lane (1955) |
|
This chapter is divided into three sections. Section 6.1 contains a review of statistics and probability concepts useful in engineering hydrology. Section 6.2 describes techniques of flood #frecuency analysis. Section 6.3 discusses low-flow frequency and droughts. |
|
Este capítulo se divide en tres secciones. Las sección 6.1 contiene un resumen de conceptos de probabilidad y estadística útil en la ingeniería hidrológica. La sección 6.2 describe técnicas de analisis de frecuencia de avenidas. La sección 6.3 trata sobre las frecuencias de flujos bajos y de seqías. |
6.1 CONCEPTOS DE ESTADÍSTICA
|
|
Introducción
The term frequency analysis refers to the techniques whose objective is to analyze the occurrence of hydrologic variables within a statistical framework, i.e., by using measured data and basing predictions on statistical laws. These techniques are applicable to the study of statistical properties of either rainfall or runoff (flow) series. In engineering hydrology, however, frequency analysis is commonly used to calculate flood discharges.
El término análisis de frecuencia se refiere a las técnicas cuyo objetivo es analizar la incidencia de las variables hidrológicas dentro de un marco estadístico, es decir, mediante el uso de datos medidos y basar las predicciones sobre leyes estadísticas. Estas técnicas son aplicables al estudio de las propiedades estadísticas de cualquiera de de las series de precipitaciones o escorrentía (flujo). En ingeniería hidrológica, sin embargo, el análisis de frecuencia es de uso común para el cálculo de las descargas de avenida.
In principle, techniques of frequency analysis are applicable to gaged catchments with long periods of streamflow record. In practice, these techniques are primarily used for large catchments, because these are more likely to be gaged and have longer record periods. Frequency analysis is also applicable to midsize catchments, provided the record length is adequate. For ungaged catchments (either midsize or large), frequency analysis can be used in a regional context to develop flow characteristics applicable to hydrologically homogeneous regions. These techniques comprise what is referred to as regional analysis (Chapter 7).
En principio, las técnicas de análisis de frecuencia son aplicables a las cuencas amordazada con largos períodos de registro de caudal. En la práctica, estas técnicas son principalmente usados para las grandes cuencas, ya que estos son más propensos a ser amordazada y tienen periodos de registro más largos. El análisis de frecuencia es también aplicable a las cuencas de tamaño medio, siempre que la longitud del registro es adecuada. Para cuencas ungaged (ya sea de tamaño mediano o grande), análisis de frecuencia se puede utilizar en un contexto regional para desarrollar características de flujo aplicables a regiones hidrológicamente homogéneas. Estas técnicas comprenden lo que se conoce como análisis regional (capítulo 7).
The question to be answered by flow frequency analysis can be stated as follows: Given n years of daily streamflow records for stream S, what is the maximum (or minimum) flow Q that is likely to recur with a frequency of once in T years on the average? Or, what is the maximum flow Q associated with a T-year return period? Alternatively, frequency analysis seeks to answer the inverse question: What is the return period T associated with a maximum (or minimum) flow Q?
La pregunta a responder por los análisis de frecuencia de flujo puede enunciarse de la siguiente manera: Dadas n años de registros de caudales diarios de corriente S, ¿cuál es el flujo máximo (o mínimo) Q que es probable que se repita con una frecuencia de una vez en T años en la media? O, cuál es el flujo máximo Q asociado con un periodo de retorno T-año? Por otra parte, el análisis de frecuencia trata de responder a la pregunta inversa: ¿Cuál es el período de retorno T asociado con un flujo máximo (o mínimo) Q?
In more general terms, the preceding questions can be stated as follows: Given n years of streamflow data for stream S and L years of design life of a certain structure, what is the probability P of a discharge Q being exceeded at least once during the design life L? Alternatively, what is the discharge Q which has the probability P of being exceeded during the design life L?
En términos más generales, las preguntas anteriores pueden expresarse de la siguiente manera: Dadas n años de datos de caudal para la corriente S y L años de vida de diseño de una determinada estructura, ¿cuál es la probabilidad P de una descarga Q se exceda por lo menos una vez durante la vida de diseño L? Por otra parte, ¿cuál es la descarga Q que tiene la probabilidad P de que se superen durante la vida de diseño L?
Random Variables
Variables Aleatorias
Frequency analysis uses random variables and probability distributions. A random variable follows a certain probability distribution. A probability distribution is a function that expresses in mathematical terms the relative chance of occurrence of each of all possible outcomes of the random variable. In statistical notation, P (X = x1) is the probability P that the random variable X takes on the outcome x1. A shorter notation is P (x1).
El análisis de frecuencia utiliza variables aleatorias y distribuciones de probabilidad. Una variable aleatoria sigue una cierta distribución de probabilidad. Una distribución de probabilidad es una función que expresa en términos matemáticos la oportunidad relativa de ocurrencia de cada uno de todos los posibles resultados de la variable aleatoria. En la notación estadística, P (X = x1) es la probabilidad P de que la variable aleatoria X toma el resultado x1. Una notación más corta es P (x1).
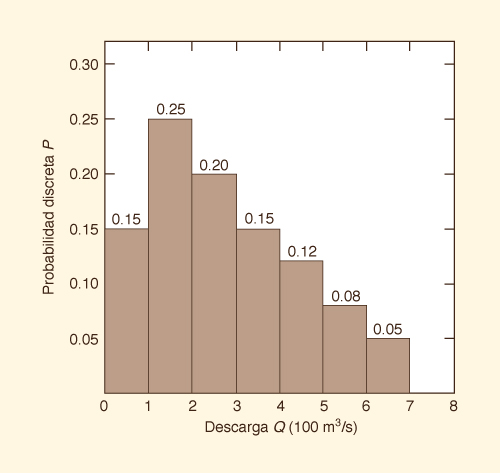
An example of random variable and probability distribution is shown in Fig. 6-1. This is a discrete probability distribution because the possible outcomes have been arranged into groups (or classes). The random variable is discharge Q; the possible outcomes are seven discharge classes, from 0-100 m3/s to 600-700 m3/s. In Fig. 6-1, the probability that Q is in the class 100-200 m3/s is 0.25. The sum of probabilities of all possible outcomes is equal to 1.
Un ejemplo de la variable aleatoria y la dsitribución de probabilidad se muestra en la Fig. 6-1. Esta es una distribución de probabilidad discreta porque los posibles resultados se han organizado en grupos (o clases). La variable aleatoria es la descarga Q; los posibles resultados son siete clases de descarga, de 0-100 m3/s a 600-700 m3/s. En la Fig. 6-1, la probabilidad de que Q está en la clase 100 a 200 m3/s is 0.25. La suma de las probabilidades de todos los resultados posibles es igual a 1.
Figure 6-1 Discrete Probability Distribution. / Distribución de Probabilidad Discreta. |
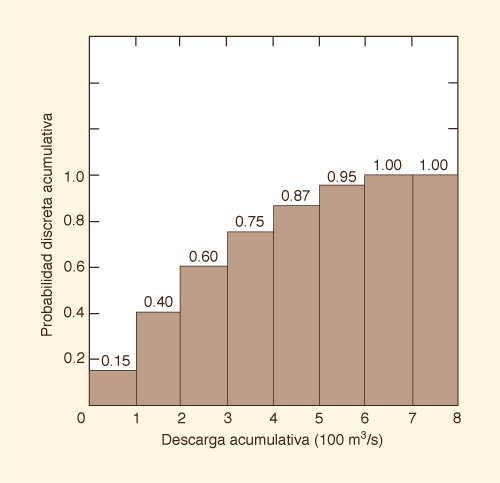
A cumulative discrete distribution, corresponding to the discrete probability distribution of Fig. 6-1, is shown in Fig. 6-2. In this figure, the probability that Q is in a class less than or equal to the 100-200 m3/s class is 0.40. The maximum value of probability of the cumulative distribution is 1.
Una distribución discreta acumulativa, correspondiente a la distribución de probabilidad discreta de la Fig. 6-1, se muestra en la Fig. 6-2. En esta figura, la probabilidad de que Q está en una clase inferior o igual a la clase de 100-200 m3/s es 0.40. El valor máximo de la probabilidad de la distribución acumulativa es 1.
Figure 6-2 Cumulative Discrete Probability Distribution./ Distribución de Probabilidad Discreta Acumulativa. |
Properties of Statistical Distributions
Propiedades de las Distribuciones Estadísticas
The properties of statistical distributions are described by the following measures: Las propiedades de las distribuciones estadísticas se describen mediante las siguientes medidas:
- Central tendency,
Tendencia central,
- Variability, and
Variabilidad y
- Skewness.
Oblicuidad.
Statistical distributions are described in terms of moments. The first moment describes central tendency, the second moment describes variability, and the third moment describes skewness. Higher order moments are possible but are seldom used in practical applications.
Las distribuciones estadísticas se describen en términos de momentos. El primer momento describe la tendencia central, el segundo momento describe la variabilidad y el tercer momento describe la asimetría. Momentos de orden superior son posibles, pero rara vez se utilizan en aplicaciones prácticas.
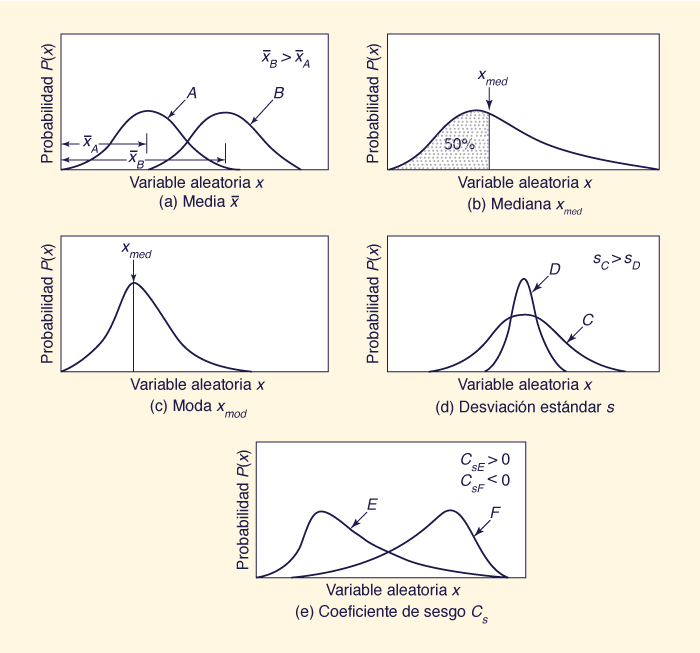
The first moment about the origin is the arithmetic mean, or mean. It expresses the distance from the origin to the centroid of the distribution, as shown in Fig. 6-3 (a):
El primer momento sobre el origen es la media aritmética, o media. Expresa la distancia desde el origen al centroide de la distribución, como se muestra en la Fig. 6-3 (a):
|
1 n x̄ = ____ Σ xi n i =1 | (6-1) |
in which x̄ is the mean, xi is the random variable, and n is the number of values.
en la que x̄ es la media, xi es la variable aleatoria, y n es el número de valores.
The geometric mean is the nth root of the product of n terms:
La media geométrica es la raíz enésima del producto de n términos:
| x̄ = (x1 x2 x3 . . . xn)1/n | (6-2) |
The logarithm of the geometric mean is the mean of the logarithms of the individual values. The geometric mean is to the lognormal probability distribution what the arithmetic mean is to the normal probability distribution.
El logaritmo de la media geométrica es la media de los logaritmos de los valores individuales. La media geométrica es la distribución de probabilidad logarítmica normal lo que es la media aritmética de la distribución de probabilidad normal.
The median is the value of the variable that divides the probability distribution into two equal portions (or areas); see Fig. 6-3 (b). For certain skewed distributions (i.e., one with third moment other than zero), the median is a better indication of central tendency than the mean. Another measure of central tendency is the mode, defined as the value of the variable that occurs most frequently; see Fig. 6-3 (c).
La mediana es el valor de la variable que divide la distribución de probabilidad en dos porciones iguales (o áreas); véase la Fig. 6-3 (b). Para ciertas distribuciones asimétricas (es decir, uno con tercer momento distinto de cero), la mediana es una mejor indicación de la tendencia central que la media. Otra medida de la tendencia central es el modo, que se define como el valor de la variable que se produce con más frecuencia; véase la Fig. 6-3 (c).
Fig. 6-3 Properties of statistical distributions./ Propiedades de las distribuciones estadísticas. |
Statistical moments can be defined about axes other than the origin. The second moment about the mean is the variance, defined as
Momentos estadísticos se pueden definir alrededor de ejes que no sean el origen. El segundo momento respecto a la media es la varianza, definida como
|
1 n s 2 = ________ Σ ( xi - x̄ ) 2 n - 1 i =1 | (6-3) |
in which s 2 is the variance. The square root of the variance, s, is the standard deviation. The variance coefficient (or coefficient of variation) is defined as
en el que s2 es la varianza. La raíz cuadrada de la varianza, s, es la desviación estándar. El coeficiente de varianza (o coeficiente de variación) se define como
|
s Cv = ____ x̄ | (6-4) |
The standard deviation and variance coefficient are useful in comparing relative variability among distributions. The larger the standard deviation and variance coefficient, the larger the spread of the distribution; see Fig. 6-3 (d).
La desviación estándar y el coeficiente de varianza son útiles en la comparación de la variabilidad relativa entre distribuciones. Cuanto mayor sea la desviación estándar y el coeficiente de varianza, mayor es la dispersión de la distribución; véase la fig. 6-3 (d).
The third moment about the mean is the skewness, defined as follows:
El tercer momento alrededor de la media es la asimetría, definido como sigue:
|
n n a = _______________ Σ ( xi - x̄ )3 (n - 1)(n - 2) i =1 | (6-5) |
in which a is the skewness. The skew coefficient is defined as
en la que a es la asimetría. El coeficiente de asimetría se define como
|
a Cs = ____ s3 | (6-6) |
For symmetrical distributions, the skewness is 0 and Cs = 0. For right skewness (distributions with the long tail to the right), Cs > 0; for left skewness (long tail to the left), Cs < 0; see Fig. 6-3 (e).
Para distribuciones simétricas, la asimetría es 0 y Cs = 0. Para la asimetría derecha (distribuciones con la larga cola a la derecha), Cs > 0; de la asimetría izquierda (larga cola a la izquierda), Cs < 0; véase la Fig. 6-3 (e).
Another measure of skewness is Pearson's skewness, defined as the ratio of the difference between mean and mode to the standard deviation.
Otra medida de la asimetría es la asimetría de Pearson, definida como la relación de la diferencia entre la media y el modo de la desviación estándar.
*****1609022230****
Example 6-1.
Calculate the mean, standard deviation, and skew coefficient for the following flood series:
4580, 3490, 7260, 9350, 2510, 3720, 4070, 5400, 6220, 4350, and 5930 m3/ s.
Calcula la media, la desviación estándar y el coeficiente de asimetría para la siguiente serie de avenidas: 4580, 3490, 7260, 9350, 2510, 3720, 4070, 5400, 6220, 4350 y 5930 m3/ s.
The calculations are shown in Table 6-1.
Column 1 shows the year and Col. 2 shows the annual maximum flows.
The mean (Eq. 6-1) is calculated by summing up Col. 2 and dividing the sum by n = 11.
This results in x̄ = 5171 m3/s.
Column 3 shows the flow deviations from the mean, xi - x̄.
Column 4 shows the square of the flow deviations, (xi - x̄ )2.
The variance (Eq. 6-3) is calculated by summing up Col. 4 and dividing the sum by (n - 1) = 10.
This results in: s 2 = 3,780,449 m6/ s2.
The square root of the variance is the standard deviation: s = 1944 m3/s.
The variance coefficient (Eq. 6-4) is Cv = 0.376.
Column 5 shows the cube of the flow deviations, ( xi - x̄ )3.
The skewness (Eq. 6-5) is calculated by summing up Col. 5 and multiplying
the sum by n / [(n - 1)(n - 2)] = 11/90.
This results in a = 6,717,359,675 m9/s3.
The skew coefficient (Eq. 6-6) is equal to the skewness divided by the cube of the standard deviation.
This results in Cs = 0.914.
Los cálculos se muestran en la Tabla 6-1.
La Columna 1 muestra el año y Col. 2 muestra los caudales máximos anuales.
La media (Ec. 6-1) se calcula mediante la suma de Col. 2 y dividiendo la suma por n = 11.
Esto resulta en x̄ = 5171 m3/s.
Columna 3 muestra las desviaciones del flujo de la media, xi - x̄.
La Columna 4 muestra el cuadrado de las desviaciones de flujo,
(xi - x̄ )2.
La varianza (Ec. 6-3) se calcula mediante la suma de la Col. 4 y dividiendo la suma por (n - 1) = 10.
Esto se traduce en: s 2 = 3,780,449 m6/ s2.
La raíz cuadrada de la varianza es la desviación estándar: s = 1944 m 3/s.
El coeficiente de variación (Ec. 6-4) es Cv = 0.376.
La columna 5 muestra el cubo de las desviaciones de flujo,
( xi - x̄ )3.
La asimetría (Ec. 6-5) se calcula mediante la suma de la Col. 5 y multiplicando
la suma por n / [(n - 1)(n - 2)] = 11/90.
Esto se traduce en a = 6,717,359,675 m9/s3.
El coeficiente de asimetría (Ec. 6-6) es igual a la asimetría dividida por el cubo de la desviación estándar.
Esto se traduce en Cs = 0.914.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Continuous Probability Distributions
Distribuciones de Probabilidad Continuas
A continuous probability distribution is referred to as a probability density function (PDF). A PDF is an equation relating probability, random variable, and parameters of the distribution. Selected PDFs useful in engineering hydrology are described in this section.
Una distribución de probabilidad continua se conoce como una función de densidad de probabilidad (PDF). Un PDF es una ecuación que relaciona la probabilidad, variable aleatoria, y los parámetros de la distribución. Los PDFs seleccionados son útiles en la ingeniería hidrológica se describen en esta sección.
Normal Distribution. The normal distribution is a symmetrical, bell-shaped PDF also known as the Gaussian distribution, or the natural law of errors. It has two parameters: the mean μ, and the standard deviation σ, of the population. In practical applications, the mean x̄ and the standard deviation s derived from sample data are substituted for μ and σ, respectively. The PDF of the normal distribution is:
Distribución Normal. La distribución normal es simétrica, en forma de campana PDF también conocida como la distribución de Gauss, o la ley natural de errores. Tiene dos parámetros: la media μ y la desviación estándar σ de la población. En las aplicaciones prácticas, la media x̄ y la desviación estándar s derivado de datos de la muestra se sustituyen por μ y σ, respectivamente. El PDF de la distribución normal es:
|
1 f (x) = __________ e - (x - μ)2 / (2σ2) σ (2π)1/2 | (6-7) |
in which x is the random variable and f (x) is the continuous probability.
en la que x es la variable aleatoria y f (x) es la probabilidad continua.
By means of the transformation
Por medio de la transformación
|
x - μ z = ________ σ | (6-8) |
the normal distribution can be converted into a one-parameter distribution, as follows:
la distribución normal se puede convertir en una distribución de un parámetro, como sigue:
|
1 f (z) = ________ e-z 2/2 (2π)1/2 | (6-9) |
in which z is the standard unit, which is normally distributed with zero mean and unit standard deviation.
en el que z es la unidad estándar, que se distribuye normalmente con una media cero y una desviación estándar unitaria.
From Eq. 6-8:
****1609051610***
| x = μ + z σ | (6-10) |
in which z, the standard unit, is the frequency factor of the normal distribution. In general, the frequency factor of a statistical distribution is referred to as K.
en la que z, la unidad estándar, es el factor de frecuencia de la distribución normal. En general, el factor de frecuencia de una distribución estadística se conoce como K.
A cumulative density function (CDF) can be derived by integrating the probability density function. From Eq. 6-9, integration leads to
Una función de densidad acumulativa (CDF) se puede derivar mediante la integración de la función de densidad de probabilidad. A partir de la Ec. 6-9, la integración conduce a
|
1 z F (z) = ________ ∫ e-u 2/2 du (2π)1/2 -∞ | (6-11) |
in which F(z) denotes cumulative probability and u is a dummy variable of integration. The distribution is symmetrical with respect to the origin; therefore, only half of the distribution needs to be evaluated. Table A-5 (Appendix A) shows values of F(z) versus z, in which F(z) is integrated from the origin to z.
en la que F(z) denota la probabilidad acumulativa y u es una variable ficticia de la integración. La distribución es simétrica con respecto al origen; por lo tanto, sólo la mitad de la distribución debe ser evaluado. Table A-5 (Apéndice A) muestra los valores de F(z) versus z, en la que F(z) está integrado desde el origen hasta z.
Example 6-2./
The annual maximum flows of a certain stream have been found to be normally distributed, with mean 90 m3/s and standard deviation 30 m3/s.
Calcuiate the probability that a flow larger that 150 m3/s will occur.
Se han encontrado los caudales máximos anuales de un determinado flujo que se distribuye normalmente, con una media de 90 m 3/s y la desviación estándar de 30 m3/s.
Calcuiate la probabilidad de que un mayor flujo que 150 m3/s ocurrirá.
To enter Table A-5, it is necessary to calculate the standard unit.
For a flow of 150 m3/s, the standard unit (Eq. 6-8) is: z = (150 - 90)/ 30 = 2.
This means that the flow of 150 m3/s is located two standard deviations to the right of the mean (had z been negative, the flow would have been located to the left of the mean).
In Table A-5, for z = 2, F(z) = 0.4772.
This value is the cumulative probability measured from z = 0 to z = 2, i.e.,
from the mean (90 m3/s) to the value being considered (150 m3/s).
Because the normal distribution is symmetrical with respect to the origin, the cumulative probability measured from z = - ∞ to z = 0, is 0.5.
Therefore, the cumulative probability measured from z = -∞ to z = 2, is F(z) = 0.5 + 0.4772 = 0.9772.
This is the probability that the flow is less than 150 m3/s.
To find the probability that the flow is larger than 150 m3/s,
the complementary cumulative probability is calculated: G(z)= 1 - F(z) = 0.0228.
Therefore, there is a (0.0228 × 100) = 2.28% chance that the annual maximum flow for the given stream will be larger than 150 m3/s.
Para entrar en la Tabla A-5, es necesario calcular la unidad estándar.
Para un flujo de 150 m 3/s, la unidad estándar (Ec. 6-8.) Es: z = (150-90)/ 30 = 2. Esto significa que el flujo de 150 m 3/s sitúa dos desviaciones estándar a la derecha de la media (había z sido negativo, el flujo se habría situado a la la izquierda de la media). En la Tabla A-5, para z = 2, F(z) = 0.4772.
Este valor mide la probabilidad acumulativa de z = 0 y z = 2, es decir,
a partir de la media (90 m3/ s) para el valor que se considera (150 m3/s).
Debido a la distribución normal es simétrica con respecto al origen, la probabilidad acumulada se mide desde z = - ∞ de z = 0, es de 0.5.
Por lo tanto, la probabilidad acumulada se mide desde z = - ∞ a z = 2, es F(z) = 0.5 + 0.4772 = 0.9772.
Esta es la probabilidad de que el flujo es menos de 150 m 3/s.
Para encontrar la probabilidad de que el flujo es mayor que 150 m3/s,
la probabilidad acumulativa complementaria se calcula: G (z) = 1 - F(z) = 0.0228.
Por lo tanto, hay un (0.0228 × 100) = 2.28% de probabilidad de que el flujo máximo anual para el flujo dado será mayor que 150 m 3/s.
|
****1609051700*****
Lognormal Distribution. / Distribución Logarítmica Normal For certain natural phenomena, values of random variables do not follow a normal distribution, but their logarithms do. In this case, a suitable PDF can be obtained by substituting y for x in the equation for the normal distribution, Eq. 6-7, in which y = ln (x). The parameters of the lognormal distribution are the mean and standard deviation of y : μy and σy.
Para ciertos fenómenos naturales, los valores de variables aleatorias no siguen una distribución normal, pero sus logaritmos hacen. En este caso, una PDF adecuada se puede obtener mediante sustitución y para x en la ecuación para la distribución normal, la Ec. 6-7, en la que y = ln (x). Los parámetros de la distribución lognormal son la media y la desviación estándar de y : μy y σy.
Gamma Distribution. / Distribución Gamma.
The gamma distribution is used in many applications of engineering hydrology. The PDF of the gamma distribution is the following:
La distribución gamma se utiliza en muchas aplicaciones de ingeniería hidrológica. El PDF de la distribución gamma es el siguiente:
|
x γ - 1 e-x/β f (x) = _____________ β γ Γ(γ) | (6-12) |
for 0 < x < ∞, β > 0, and γ > 0. The parameter γ is known as the shape parameter, since it most influences the peakedness of the distribution, while the parameter β is called the scale parameter, since most of its influence is on the spread of the distribution [4].
para 0 < x < ∞, β > 0, y γ > 0. El parámetro γ se conoce como el parámetro de forma, ya que más influye en el apuntamiento de la distribución, mientras que el parámetro β se llama el parámetro de escala, ya que la mayor parte de su influencia está en la propagación de la distribución de [4].
The mean of the gamma distribution is βγ, the variance is β2γ, and the skewness is 2/γ1/2. The term Γ(γ) = (γ - 1)! , in which γ is a positive integer, is an important definite integral referred to as the gamma function, defined as follows:
La media de la distribución gamma es βγ, la varianza es β2γ, y la asimetría es 2/γ1/2. El término Γ(γ) = (γ - 1)! , En la que γ es un entero positivo, es una integral definida importante denominada la función gamma, se define como sigue:
|
∞ Γ(γ) = ∫ x γ - 1 e-x dx 0 | (6-13) |
Pearson Distributions./ Distribuciones de Pearson. Pearson [24] has derived a series of probability functions to fit virtually any distribution. These functions have been widely used in practical statistics to define the shape of many distribution curves.The general PDF of the Pearson distributions is the following [6]:
Pearson [24] ha derivado una serie de funciones de probabilidad para adaptarse virtualmente a cualquier distribución. Estas funciones han sido ampliamente utilizados en las estadísticas prácticas para definir la forma de muchas curvas de distribución. El PDF general de las distribuciones de Pearson es el siguiente [6]:
|
x ∫ [( a + x ) / ( b0 + b1x + b2x2 )] dx -∞ f (x) = e | (6-14) |
in which a, b0 , b1, b2 are constants. The criterion for determining the type of distribution is κ, defined as follows:
en el que a, b0, b1, b2 son constantes. El criterio para determinar el tipo de distribución es κ, definida como sigue:
|
β1( β2 + 3)2 κ = ________________________________ 4 (4β2 - 3β1) (2β2 - 3β1 - 6) | (6-15) |
in which β1 = μ32/μ23 and β2 = μ4/μ22, with μ2, μ3, and μ4 being the second, third, and fourth moments about the mean. With μ3 = 0 (i.e., zero skewness), β1 = 0, κ = 0, and the Pearson distribution reduces to the normal distribution.
en el cual β1 = μ32/μ23 y β2 = μ4/μ 22, con μ2, μ3, y μ4 siendo el segundo, tercer y cuarto momentos con respecto a la media. Con μ3 = 0 (es decir, cero asimetría), β1 = 0, κ = 0, y la distribución Pearson reduce a la distribución normal.
The Pearson Type III distribution has been widely used in flood frequency analysis. In the Pearson Type III distribution, κ = ∞, which implies that 2β2 = (3β1 + 6). This is a three-parameter skewed distribution with the following PDF:
La distribución Pearson Tipo III ha sido ampliamente utilizado en el análisis de frecuencia de avenida. En la distribución Pearson Tipo III, κ = ∞, lo que implica que 2β2 = (3β1 + 6). Se trata de una distribución asimétrica de tres parámetros con el siguiente PDF:
|
(x - xo)γ - 1 e - (x - xo) /β f (x) = _________________________ βγ Γ(γ) | (6-16) |
and parameters β, γ, and xo. For xo = 0, the Pearson Type III distribution reduces to the gamma distribution (Eq. 6-12). For γ = 1, the Pearson Type III distribution reduces to the exponential distribution, with the following PDF:
y los parámetros β, γ, y xo. Para xo = 0, la distribución Pearson Tipo III se reduce a la distribución gamma (Ec. 6-12). For γ = 1, la distribución de Pearson Tipo III se reduce a la distribución exponencial, con el siguiente PDF:
|
1 f (x) = (____) e- (x - xo) /β β | (6-17) |
The mean of the Pearson Type III distribution is: xo + βγ;
the variance is: β2γ; and
the skewness is:
La media de la distribución Pearson Tipo III es: xo + βγ;
la varianza es: β2γ; y
la asimetría es:
Extreme Value Distributions. / Distribuciones de Valor Extremo The extreme value distributions Types I, II, and III are based on the theory of extreme values. Frechet (on Type II) in 1927 [8] and Fisher and Tippett (on Types I and III) in 1928 [8] independently studied the statistical distribution of extreme values. Extreme value theory implies that if a random variable Q is the maximum in a sample of size n from some population of x values, then, provided n is sufficiently large, the distribution of Q is one of three asymptotic types (I, II, or III), depending on the distribution of x.
Las distribuciones de valor extremo Tipos I, II, y III se basan en la teoría de los valores extremos. Frechet (el tipo II) en 1927 [8] y Fisher y Tippett (en los tipos I y III) en 1928 [8] estudiaron de forma independiente la distribución estadística de valores extremos. La teoría del valor extremo implica que si una variable aleatoria Q es el máximo en una muestra de tamaño n de alguna población de valores de x, entonces, siempre que n es suficientemente grande, la distribución de Q es uno de los tres tipos asintóticas (I, II, o III), dependiendo de la distribución de x.
The extreme value distributions can be combined into one and expressed as a general extreme value (GEV) distribution [23]. The cumulative density function of the GEV distribution is:
Las distribuciones de valores extremos se pueden combinar en uno y se expresaron como un valor extremo general (GEV) de distribución [23]. La función de densidad acumulada de la distribución GEV es:
| F ( x ) = e - [1 - k ( x - u ) / α]1/k | (6-18) |
in which k, u and α are parameters. The parameter k defines the type of distribution, u is a location parameter, and α is a scale parameter. For k = 0, the GEV distribution reduces to the extreme value Type I (EV1), or Gumbel distribution. For k < 0, the GEV distribution is the extreme value Type II (EV2), or Frechet distribution. For k > 0, the GEV distribution is the extreme value Type III (EV3), or Weibull distribution. The GEV distribution is useful in applications where an extreme value distribution is being considered but its type is not known a priori.
en la que k, u y α son parámetros. El parámetro k define el tipo de distribución, u es un parámetro de localización, y α un parámetro de escala. Para k = 0, la distribución GEV reduce al valor extrema Tipo I (EV1), o la distribución Gumbel. Para k < 0, la distribución GEV es la extrema Tipo de valor II (EV2), o la distribución Fréchet. Para k > 0, la distribución GEV es la extrema Tipo de valor III (EV3), o la distribución de Weibull. La distribución GEV es útil en aplicaciones en las que se está considerando una distribución de valor extremo, pero su tipo no se conoce a priori.
Gumbel [13, 14, 15, 16] has fitted the extreme value Type I distribution to long records of river flows from many countries. The cumulative density function (CDF) of the Gumbel distribution is the following double exponential function:
Gumbel [13, 14, 15, 16] ha ajustado la distribución Tipo I de valor extremo para registros largos del flujo del río de varios países. La función de densidad acumulativa (CDF) de la distribución Gumbel es la siguiente función exponencial doble:
| F ( x ) = e -e -y | (6-19) |
in which y = (x - u)/α is the Gumbel (reduced) variate.
en la que y = (x - u)/α es la variable Gumbel (reducido).
The mean ȳn and standard deviation σn of the Gumbel variate are functions of record length n. Values of ȳn and σn as a function of n are given in Table A-8 (Appendix A). When the record length approaches ∞, the mean ȳn approaches the value of the Euler constant (0.5772) [29], and the standard deviation σn approaches the value π /61/2. The skew coefficient of the Gumbel distribution is 1.14.
El media ȳ n y desviación estándar σn de la variable Gumbel son funciones de la longitud de registro n. Los valores de ȳn y σn como una función de n se dan en la Tabla A-8(Apéndice A). Cuando la longitud de registro se aproxima ∞, la media ȳn se acerca al valor de la constante de Euler (0.5772) [29], y la desviación estándar σnn se acerca al valor π /61/2. El coeficiente de asimetría de la distribución Gumbel es 1.14.
The extreme value Type II distribution is also known as the log Gumbel. Its cumulative density function is:
La distribución de valores extremos Tipo II también se conoce como el logaritmo de Gumbel. Su función de densidad acumulativa es:
| F ( x ) = e -y 1/k | (6-20) |
for k < 0.
para k < 0.
The extreme value Type III distribution has the same CDF as the Type II, but in this case k > 0. As k approaches 0, the EV2 and EV3 distributions converge to the EV1 distribution.
El valor extremo de distribución Tipo III tiene el mismo CDF como el Tipo II, pero en este caso k > 0. Como k se aproxima a 0, las distribuciones EV2 y EV3 convergen a la distribución EV1.
6.2 ANÁLISIS DE FRECUENCIA
|
|
Flood frequency analysis refers to the application of frequency analysis to study the occurrence of floods. Historically, many probability distributions have been used for this purpose. The normal distribution was first used by Horton [19] in 1913, and shortly thereafter by Fuller [11]. Hazen [17] used the lognormal distribution to reduce skewness, whereas Foster [9] preferred to use the skewed Pearson distributions.
Los análisis de frecuencia de avenida se refiere a la aplicación de análisis de frecuencia para estudiar la incidencia de avenidas. Históricamente, muchas distribuciones de probabilidad se han utilizado para este propósito. La distribución normal se utilizó por primera vez por Horton [19] en 1913, y poco después por Fuller [11]. Hazen [17] utiliza la distribución lognormal para reducir la asimetría, mientras que Foster [9] prefiere usar las distribuciones asimétricas de Pearson.
The logarithmic version of the Pearson Type III distribution, i.e., the log Pearson III, has been endorsed by the U.S. Interagency Advisory Committee on Water Data for general use in the United States [31]. The Gumbel distribution (extreme value Type I, or EVl) is also widely used in the United States and throughout the world. The log Pearson III and Gumbel methods are described in this section.
La versión logarítmica de la distribución Tipo III de Pearson, es decir, el logaritmo de Pearson III, ha sido aprobado por el Comité Consultivo Interinstitucional de EE.UU. en Datos sobre el Agua para uso general en los Estados Unidos [31]. La distribución Gumbel (valor extremo Tipo I, o EVI) también es ampliamente utilizado en los Estados Unidos y en todo el mundo. Los métodos de logaritmo de Pearson III y Gumbel se describen en esta sección.
Selection of Data Series / La Selección de Series de Datos
The complete record of streamflows at a given gaging station is called the complete duration series. To perform a flood frequency analysis, it is necessary to select a flood series, i.e., a sample of flood events extracted from the complete duration series.
El registro completo de los caudales en la estación de aforo determinado se llama series de duración completas. Para realizar un análisis de frecuencia de avenida, es necesario seleccionar una serie de avenidas , es decir, una muestra de los eventos de avenidas extraídos de la serie de duración completa.
There are two types of flood series: (1) the partial duration series and (2) the extreme value series. The partial duration (or peaks-over-a-threshold (POT) [23] series consists of floods whose magnitude is greater than a certain base value. When the base value is such that the number of events in the series is equal to the number of years of record, the series is called an annual exceedance series.
Hay dos tipos de series de avenidas: (1) las series de duración parcial y (2) la serie de valores extremos. Las series de duración parcial (o picos-sobre-un-umbral (POT) [23] serie consta de avenidas cuya magnitud es mayor que un valor base determinado. Cuando el valor de base es tal que el número de eventos de la serie es igual a la número de años de registro, la serie se llama una serie anual de excedencia.
In the extreme value series, every year of record contributes one value to the extreme value series, either the maximum value (as in the case of flood frequency analysis) or the minimum value (as in the case of low-flow frequency analysis). The former is the annual maxima series; the latter is the annual minima series.
En la serie de valores extremos, cada año de registro contribuye con un valor a la serie de valores extremos, ya sea el valor máximo (como en el caso del análisis de frecuencia de avenida) o el valor mínimo (como en el caso del análisis de frecuencia de bajo flujo). El primero son las series máximas anuales; esta última es la serie mínima anual.
****1609061230****
The annual exceedance series takes into account all extreme events above a certain base value, regardless of when they occurred. However, the annual maxima series considers only one extreme event per yearly period. The difference between the two series is likely to be more marked for short records in which the second largest annual events may strongly influence the character of the annual exceedance series. In practice, the annual exceedance series is used for frequency analyses involving short return periods, ranging from 2 to 10 y. For longer return periods the difference between annual exceedance and annual maxima series is small. The annual maxima series is used for return periods ranging from 10 to 100 y and more.
La serie anual de excedencia tiene en cuenta todos los eventos extremos por encima de cierto valor base, independientemente del momento en que ocurrieron. Sin embargo, la serie máxima anual considera sólo un evento extremo por período anual. La diferencia entre las dos series es probable que sea más marcado para los registros cortos en los que los segundos eventos anuales mayores pueden influir fuertemente el carácter de la serie anual de excedencia. En la práctica, la serie anual de excedencia se usa para los análisis de frecuencia que implica períodos de retorno cortos, que van desde 2 a 10 y. Para períodos de retorno más largos la diferencia entre excedencia anual y serie máxima anual es pequeño. La serie máxima anual se utiliza para períodos de retorno de 10 a 100 y más.
Return Period, Frequency, and Risk/ Período de Retorno, Frecuencia, y Riesgo
The time elapsed between successive peak flows exceeding a certain flow Q is a random variable whose mean value is called the return period T (or recurrence interval) of the flow Q. The relationship between probability and return period is the following:
El tiempo transcurrido entre los flujos pico sucesivos superior a un cierto flujo de Q es una variable aleatoria cuyo valor medio se llama el período de retorno T (o intervalo de recurrencia) del flujo de Q. La relación entre la probabilidad y el período de retorno es el siguiente:
*****1609061424*****
|
1 P(Q) = ____ T | (6-21) |
in which P(Q) is the probability of exceedance of Q, or frequency. The terms frequency and return period are often used interchangeably, although strictly speaking, frequency is the reciprocal of return period. A frequency of 1/T, or one in T years, corresponds to a return period of T years.
en el que P(Q) es la probabilidad de excedencia de Q, o frecuencia. La frecuencia de los términos y período de retorno se usan indistintamente, aunque estrictamente hablando, la frecuencia es la inversa del periodo de retorno. Una frecuencia de 1/T, o uno en T años, corresponde a un periodo de retorno de T años.
The probability of nonexceedance P(Q̄) is the complementary probability of the probability of exceedance P(Q), defined as
La probabilidad de no excedencia P(Q̄) es la probabilidad complementaria de la probabilidad de excedencia de P(Q), definida como
|
1 P(Q̄) = 1 - P(Q) = 1 - ____ T | (6-22) |
The probability of nonexceedance in n successive years is
La probabilidad de no excedencia en n años sucesivos es
|
1 n P(Q̄) = ( 1 - _____ ) T | (6-23) |
Therefore, the probability, or risk, that Q will occur at least once in n successive years is
Por lo tanto, la probabilidad, o riesgo, que Q se producirá al menos una vez en n años sucesivos es
|
1 n R = 1 - P(Q̄) = 1 - ( 1 - _____ ) T | (6-24) |
Plotting Positions/ Posiciones de Ploteo
Frequency distributions are plotted using probability papers. One of the scales on a probability paper is a probability scale; the other is either an arithmetic or logarithmic scale. Normal and extreme value probability distributions are most often used in probability papers.
Distribuciones de frecuencias se representan utilizando papeles de probabilidad. Una de las escalas de un papel de probabilidad es una escala de probabilidad; el otro es o bien una aritmética o escala logarítmica. Distribuciones de probabilidad normal y valor extremo son los más utilizados en los papeles de probabilidad. ***********************
An arithmetic probability paper has a normal probability scale and an arithmetic scale. This type of paper is used for plotting normal and Pearson distributions. A log probability paper has a normal probability scale and a logarithmic scale and is used for plotting lognormal and log Pearson distributions. An extreme value probability paper has an extreme value scale and an arithmetic scale and is used for plotting extreme value distributions.
Un papel de probabilidad aritmética tiene una escala de probabilidad normal y una escala aritmética. Este tipo de papel se utiliza para plotear las distribuciones normales y de Pearson. Un papel de probabilidad logarítmica tiene una escala de probabilidad normal y una escala logarítmica y se utiliza para plotear distribuciones de valor extremo. Un papel de probabilidad de valor extremo tiene una escala de valor extremo y una escala aritmética y se utiliza para plotear las distribuciones de valores extremos.
Data fitting a normal distribution plot as a straight line on arithmetic probability paper. Likewise, data fitting a lognormal distribution plot as a straight line on log probability paper, and data fitting the Gumbel distribution plot as a straight line on extreme value probability paper.
Los datos se ajustan a un ploteo de distribución normal como una línea recta en el papel de probabilidad aritmética. Del mismo modo, los datos de ajuste de un ploteo de distribución lognormal como una línea recta en el papel de probabilidad logarítmica, y los datos de ajustan al ploteo de distribución de Gumbel como una línea recta en el papel de probabilidad de valor extremo.
For plotting purposes, the probability of an individual event can be obtained directly from the flood series. For a series of n annual maxima, the following ratio holds:
Para los propósitos de ploteo, la probabilidad de un evento individual se puede obtener directamente de la serie de avenida. Para una serie de n máxima anual, la siguiente relación se tiene:
|
x̄ m ___ = _______ N n + 1 | (6-25) |
in which x̄ = mean number of exceedances; N = number of trials; n = number of values in the series; and m = the rank of descending values, with largest equal to 1.
en la que x̄ = media del número de superaciones; N = número de ensayos; n = número de valores en la serie; y m = el rango de valores descendentes, con mayor igual a 1.
For example, if n = 79, the second largest value in the series (m = 2) will be exceeded twice on the average (x̄ = 2) in 80 trials (N = 80). Likewise, the largest value in the series (m = 1) will be exceeded once on the average (x̄ = 1) after 80 trials (N = 80). Since return period T is associated with x̄ = 1, Eq. 6-25 can be expressed as follows:
Por ejemplo, si n = 79, el valor de la segunda mayor en la serie (m = 2) se superará el doble del promedio (x̄ = 2) en 80 ensayos (N = 80). Del mismo modo, el valor más grande de la serie (m = 1) se superará una vez en la media (x̄ = 1) después de 80 ensayos (N = 80). Desde el período de retorno T se asocia con x̄ = 1, la Ec. 6-25 se puede expresar como sigue:
|
1 m ___ = P = _______ T n + 1 | (6-26) |
in which P = exceedance probability.
en la que P = probabilidad de excedencia.
Equation 6-26 is known as the Weibull plotting position formula. This equation is commonly used in hydrologic applications, particularly for computing plotting positions for unspecified distributions [1]. A general plotting position formula is of the following form [12]:
La ecuación 6-26 se conoce como la fórmula de posición de ploteo de Weibull. Esta ecuación se utiliza comúnmente en aplicaciones hidrológicas, en particular para el cálculo de las posiciones de ploteo para distribuciones no especificadas [1]. Una fórmula general de posición de ploteo es de la siguiente forma [12]:
|
1 m - a ___ = P = _____________ T n + 1 - 2a | (6-27) |
in which a = parameter. Cunnane [7] performed a detailed study of the accuracy of different plotting position formulas and concluded that the Blom formula [3], with a = 0.375 in Eq. 6-27, is most appropriate for the normal distribution, whereas the Gringorten formula, with a = 0.44, should be used in connection with the Gumbel distribution. According to Cunnane, the Weibull formula, for which a = 0, is most appropriate for a uniform distribution.
en la que a = parámetro. Cunnane [7] realizó un estudio detallado de la exactitud de las diferentes fórmulas de posición de ploteo y llegó a la conclusión de que la fórmula Blom [3], con a = 0.375 en la Ec. 6-27, es el más apropiado para la distribución normal, mientras que la fórmula Gringorten, con a = 0.44, debe ser usada en relación con la distribución Gumbel. Según Cunnane, la fórmula de Weibull, para los que a = 0, es el más apropiado para una distribución uniforme.
In computing plotting positions, when the ranking of values is in descending order (from highest to lowest), P is the probability of exceedance, or the probability of a value being greater than or equal to the ranked value. When the ranking of values is in ascending order (from lowest to highest), P is the probability of nonexceedance, or the probability of a value being less than or equal to the ranked value. The computation of plotting positions is illustrated by the following example.
Al calcular las posiciones de ploteo, cuando la clasificación de valores está en orden descendente (de mayor a menor) descendente, P es la probabilidad de excedencia, o la probabilidad de un valor siendo mayor que o igual al valor clasificado. Cuando la clasificación de los valores es en orden ascendente (de menor a mayor), P es la probabilidad de no excedencia, o la probabilidad de un valor inferior o igual al valor clasificado. El cálculo de las posiciones de ploteo se ilustra con el siguiente ejemplo.
Example 6-3.
Use Eq. 6-26 to calculate the plotting positions for the flood series (annual maxima) shown in Table 6-2,
Utilizar la Ec. 6-26 para calcular las posiciones de ploteo para la serie de avenidas (máxima anual) que se muestra en la Tabla 6-2,
The solution is shown in Table 6-2, Cols. 3-5. Column 3 shows the ranked values, from highest to lowest.
Column 4 shows the rank of each value, from 1 to 16 (n = 16), with the highest value ranked as 1 and the lowest value ranked as 16.
Column 5 shows the probability calculated by Eq. 6-26 (expressed in percent).
Because the ranking was done in descending order, Col. 5 shows the probability that a value of flood discharge will be greater than or equal to the ranked value.
To illustrate, there is a 5.88% probability that a value of flood discharge will be greater than or equal to 3320 m3/s.
Conversely, there is a 94.12% probability that the value of flood discharge will be greater than or equal to 690 m3/s.
Column 6 shows the return period calculated by Eq. 6-26.
La solución se muestra en la Tabla 6-2, Cols. 3-5. La Columna 3 muestra los valores clasificados, de mayor a menor. La Colum 4 muestra el rango de cada valor, desde 1 a 16 (n = 16), con el valor más alto clasificado como 1 y el valor más bajo clasificado como 16. La Columna 5 muestra la probabilidad calculada por la Ec. 6-26 (expresado en porcentaje). Debido a que la clasificación se realizó en orden descendente, la Col. 5 muestra la probabilidad de que un valor de la descarga de avenida será mayor que o igual al valor clasificado. Para ilustrar esto, hay una probabilidad de 5.88% de que un valor de descarga de avenida será mayor que o igual a 3320 m3/s. Por el contrario, existe una probabilidad 94.12% de que el valor de la descarga de avenida será mayor que o igual a 690 m3/s. La Columna 6 muestra el período de retorno calculada por la Ec. 6-26.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Curve Fitting / Ajuste de Curvas
Once the data have been plotted on probability paper, the next step is to fit a curve through the plotted points. Curve fitting can be accomplished by any of the following methods: (1) graphical, (2) least square, (3) moments, and (4) maximum likelihood. The graphical method consists of fitting a function visually to the data. This method, however, has the disadvantage that the results are highly dependent on the skills of the person doing the fitting. A more consistent procedure is to use either the least square, moments, or maximum likelihood methods.
Una vez que los datos han sido ploteados en papel de probabilidad, el siguiente paso es para ajustar una curva a través de los puntos ploteados. El ajuste de curvas se puede lograr mediante cualquiera de los métodos siguientes: (1) gráfica, (2) los mínimos cuadrados, (3) momentos, y (4) de máxima verosimilitud. El método gráfico consiste en el ajuste de una función visualmente a los datos. Este método, sin embargo, tiene la desventaja de que los resultados dependen en gran medida de las habilidades de la persona que realiza la instalación. Un procedimiento más coherente es usar cualquiera de los mínimos cuadrados, momentos, o métodos de máxima verosimilitud.
In the least square method, the sum of the squares of the differences between observed data and fitted values is minimized. The minimization condition leads to a set of m normal equations, where m is the number of parameters to be estimated. The simultaneous solution of the normal equations leads to the parameters describing the fitting (Chapter 7).
En el método de mínimos cuadrados, la suma de los cuadrados de las diferencias entre los datos observados y los valores ajustados se minimizan. La condición de minimización conduce a un conjunto de m ecuaciones normales, donde m es el número de parámetros a estimar. La solución simultánea de las ecuaciones normales conduce a los parámetros que describen el ajuste (Capítulo 7).
To apply the method of moments, it is first necessary to select a distribution; then, the moments of the distribution are calculated based on the data. The method provides an exact theoretical fitting, but the accuracy is substantially affected by errors in the tail of the distribution (i.e., events of long return period). A disadvantage of the method is the uncertainty regarding the adequacy of the chosen probability distribution.
Para aplicar el método de los momentos, es primero necesario seleccionar una distribución; a continuación, los momentos de la distribución se calculan en base a los datos. El método proporciona una conexión teórica exacta, pero la precisión se ve afectada sustancialmente por errores en la cola de la distribución (es decir, acontecimientos del período de retorno de largo). Una desventaja del método es la incertidumbre en cuanto a la adecuación de la distribución de probabilidad elegida.
In the method of maximum likelihood, the distribution parameters are estimated in such a way that the product of probabilities (i.e., the joint probability, or likelihood) is maximized. This is obtained in a similar manner to the least square method by partially differentiating the likelihood with respect to each of the parameters and equating the result to zero.
En el método de máxima verosimilitud, los parámetros de la distribución se calculan de tal manera que el producto de las probabilidades (es decir, la probabilidad conjunta, o la probabilidad) se maximiza. Esto se obtiene de una manera similar al método de mínimos cuadrados diferenciando parcialmente la probabilidad con respecto a cada uno de los parámetros e igualando el resultado a cero.
The four fitting methods can be rated in ascending order of effectiveness: graphical, least square, moments, and maximum likelihood. The latter, however, is somewhat more difficult to apply [6, 21]. In practice, the method of moments is the most commonly used curve fitting method (see, for instance, the log Pearson III and Gumbel methods described later in this section).
Los cuatro métodos de ajuste pueden estar clasificados en orden ascendente de la eficacia: gráfica, mínimos cuadrados, momentos y de máxima verosimilitud. El último, sin embargo, es algo más difícil de aplicar [6, 21]. En la práctica, el método de momentos que es el más comúnmente utilizado es el método del ajuste de la curva (véase, por ejemplo, los métodos de Pearson logarítmico III y Gumbel descritos más adelante en esta sección).
Frequency Factors
Los factores de frecuencia
Any value of a random variable may be represented in the following form:
Cualquier valor de una variable aleatoria puede ser representado de la siguiente forma:
| x = x̄ + Δx | (6-28) |
in which x = value of random variable; x̄ = mean of the distribution, and Δx = departure from the mean, a function of return period and statistical properties of the distribution. This departure from the mean can be expressed in terms of the product of the standard deviation s and a frequency factor K such that Δx = K s. The frequency factor is a function of return period and probability distribution to be used in the analysis. Therefore, Eq. 6-28 can be written in the following form:
en la que x = valor de la variable aleatoria; x̄ = media de la distribución, y Δx = salida de la media, una función de período de retorno y las propiedades estadísticas de la distribución. Esta salida de la media se puede expresar en términos del producto de la desviación estándar s y un factor de frecuencia K de tal manera Δx = K s. El factor de frecuencia es una función del período de retorno y distribución de probabilidad para ser utilizado en el análisis. Por lo tanto, la Ec. 6-28 puede escribirse de la siguiente forma:
| x = x̄ + K s | (6-29) |
or, alternatively,
o alternativamente,
|
x ___ = 1 + K Cv x̄ | (6-30) |
in which Cv = variance coefficient.
en el que Cv = coeficiente de varianza.
Equation 6-29 was proposed by Chow [5] as a general equation for hydrologic frequency analysis. For any probability distribution, a relationship can be determined between frequency factor and return period. This relationship can be expressed in analytical terms, in the form of tables, or by K-T curves. In using the procedure, the statistical parameters are first determined from the analysis of the flood series. For a given return period, the frequency factor is determined from the curves or tables and the flood magnitude computed by Eq. 6-29.
La Ecuación 6-29 fue propuesto por Chow [5] como una ecuación general para el análisis de frecuencia hidrológico. Para cualquier distribución de probabilidad, una relación puede ser determinada entre el factor de frecuencia y período de retorno. Esta relación se puede expresar en términos analíticos, en forma de tablas, o por las curvas K-T. Utilizando el procedimiento, los parámetros estadísticos se determinan primero a partir del análisis de la serie de avenida. Para un período de retorno dado, el factor de frecuencia se determina a partir de las curvas o tablas y la magnitud de avenida calculada por la Ec. 6-29.
Log Pearson III Method / El Método de Log Pearson III
The log Pearson III method of flood frequency analysis is described in Bulletin 17B: Guidelines for Determining Flood Flow Frequency, published by the U.S. Interagency Advisory Committee on Water Data, Reston, Virginia [31].
El método de Log Pearson III del análisis de frecuencia de avenidas se describe en el Boletín 17B: Directrices para la Determinación de Frecuencia del Flujo de Avenida, publicado por el Comité Consultivo Interinstitucional sobre EE.UU. sobre Datos del Agua, Reston, Virginia [31].
Methodology. To apply the method, the following steps are necessary:
Metodología. Para aplicar el método, los siguientes pasos son necesarios:
Assemble the annual flood series xi.
Ensamblar la serie de avenida anual xi.
Calculate the logarithms of the annual flood series:
Calcular los logaritmos de la serie anual de avenida:
yi = log xi (6-31) Calculate the mean ȳ, standard deviation sy, and skew coefficient Csy of the logarithms yi.
Calcular la media ȳ, la desviación estándar sy, y el coeficiente de asimetría Csy de los logaritmos yi.
Calculate the logarithms of the flood discharges, log Qj for each of several chosen probability levels Pj using the following frequency formula:
Calcular los logaritmos de las descargas de avenida, log Qj para cada uno de varios niveles de probabilidad sleccionados Pj utilizando la siguiente fórmula de frecuencia:
log Qj = ȳ + Kj sy (6-32) in which Kj is the frequency factor, a function of the probability Pj and the skew coefficient Csy. Table A-6 (Appendix A) shows frequency factors K for ten selected probability levels in the range 0.5 to 95 percent (and corresponding return periods in the range 200 to 1.05 y) and skew coefficients in the range -3.0 to 3.0.
en el que Kj es el factor de frecuencia, una función de la probabilidad Pj y el coeficiente de asimetría Csy. Tabla A-6 (Apéndice A) muestra los factores de frecuencia K para diez niveles de probabilidad selectas en el intervalo de 0.5 a 95 por ciento (y períodos de retorno correspondientes en el intervalo de 200 a 1.05 y) y los coeficientes de asimetría en el rango de -3,0 a 3.0.
Calculate the flood discharges Qj for each Pj probability level (or return period Tj) by taking the antilogarithms of the log Qj values.
Calcular la descargas de avenida Qj para cada nivel de probabilidad Pj (o período de retorno Tj) mediante la adopción de los antilogaritmos de los valores del logaritmo Qj.
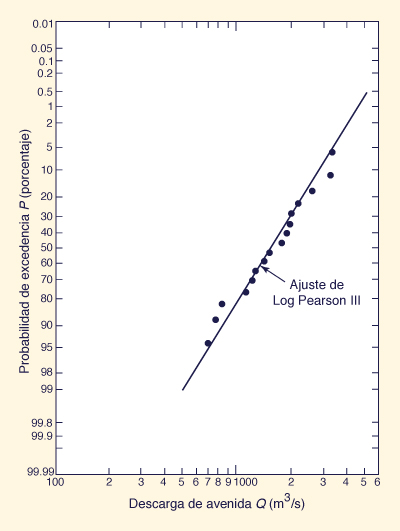
Plot the flood discharges Qj against probabilities Pj on log probability paper, with discharges in the log scale and probabilities in the probability scale. The log Pearson III fit to the data is obtained by linking the points with a smooth curve. For Csy = 0, the curve reduces to a straight line.
El ploteo de las descargas de avenida Qj contra probabilidades Pj en papel de probabilidad logarítmica, con descargas en la escala logarítmica y probabilidades en la escala de probabilidad. El logaritmo de Pearson III se ajusta a los datos obtenidos mediante la vinculación de los puntos con una curva suave. Para Csy = 0, la curva se reduce a una línea recta.
The procedure is illustrated by the following example.
El procedimiento se ilustra mediante el siguiente ejemplo.
Example 6-4.
Apply the log Pearson III method to the flood series of Example 6-3.
Plot the results on log probability paper along with the plotting positions calculated in Example 6-3.
Aplicar el método de logaritmo de Pearson III para la serie de avenida del Ejemplo 6-3.
Plotear gráficamente los resultados en papel de probabilidad logarítmica junto con las posiciones de
ploteo calculados en el Ejemplo 6-3.
The discharge values, Table 6-2, Col. 2, are converted to logarithms, and the mean, standard deviation, and skew coefficient of the logarithms calculated.
This results in ȳ = 3.187, sy = 0.207, and Csy = -0.116.
The computations are summarized in Table 6-3.
Column 1 shows selected return periods, and Col. 2 shows the associated probabilities in percent (exceedance probability).
Column 3 shows the frequency factors K for
Los valores de descarga, Tabla 6-2, Col. 2, se convierten en logaritmos, y la media, la desviación estándar y el coeficiente de asimetría de los logaritmos calculados.
Esto se traduce en ȳ = 3.187, sy = 0.207, and Csy = -0.116.
Los cálculos se resumen en la Tabla 6-3. La Columna 1 muestran los períodos de retorno seleccionados, y Col. 2 muestra las probabilidades asociadas en porcentaje (probabilidad de excedencia).
La columna 3 muestra los factores de frecuencia K
ONLINE CALCULATION. Using ONLINE PEARSON,
the results are essentially the same, varying from Q = 691 m3/s for T = 1.05 y, to Q = 4984 m3/s for T = 200 y.
CÁLCULO EN LÍNEA. Usando ONLINE PEARSON, los resultados son esencialmente los mismos, variando de Q = 691 m3/s para T = 1.05 y, a Q = 4984 m3/s para T = 200 y.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
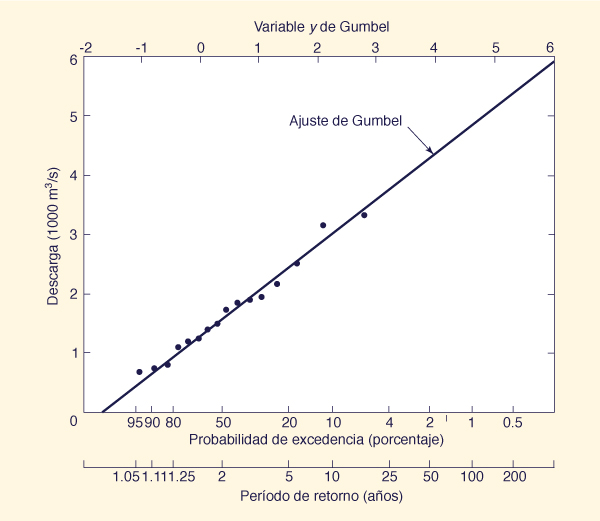
Figure 6-4 Log Pearson III fit: Example 6-4 [31]./ logaritmo de Pearson III: Ejemplo 6-4 [31]. |
Regional Skew Characteristics / Características Asimétricas Regionales
The skew coefficient of the flood series (i.e., the station skew) is sensitive to extreme events. The overall accuracy of the method is improved by using a weighted value of skew in lieu of the station skew. First, a value of regional skew is obtained, and the weighted skew is calculated by weighing station and regional skews in inverse proportion to their mean square errors (MSE). The formula for weighted skew is the following:
El coeficiente de asimetría de la serie de avenidas (es decir, la asimetría de la estación) es sensible a los fenómenos extremos. La precisión global del método se mejora mediante el uso de un valor ponderado de asimetría en lugar de la inclinación de la estación. En primer lugar, se obtiene un valor de asimetría regional, y la asimetría ponderada se calcula por la estación ponderada y las asimetrías regionales en proporción inversa a sus errores cuadráticos medios (MSE). La fórmula para la asimetría ponderada es la siguiente:
|
(MSE)sr Csy + (MSE)sy Csr Csw = ________________________________ (MSE)sr + (MSE)sy | (6-33) |
in which Csw = weighted skew; Csy = station skew; Csr = regional skew; (MSE)sy = mean square error of the station skew; and (MSE)sr = mean square error of the regional skew.
en el que Csw = asimetría ponderada; Csy = estación asimétrica; Csr = asimetría regional; (MSE)sy = error de la media cuadrada de la asimetría regional.
To develop a value of regional skew, it is necessary to assemble data from at least 40 stations or, alternatively, all stations within a 160-km radius. The stations should have at least 25 y of record. In certain cases, the paucity of data may require a relaxation of these criteria. The procedure includes analysis by three methods: (1) skew isolines map, (2) skew prediction equation, and (3) statistics of station skews.
Para desarrollar un valor de asimetría regional, es necesario reunir datos de al menos 40 estaciones o, en su defecto, todas las estaciones dentro de un radio de 160-km. Las estaciones deben tener al menos 25 años de registro. En ciertos casos, la escasez de datos puede requerir una relajación de estos criterios. El procedimiento incluye el análisis por tres métodos: (1) mapa de isolíneas asimétricas, (2) ecuación de predicción asimétrica, y (3) las estadísticas de la estación asimétrica.
To develop a skew isolines map, each station skew is plotted on a map at the centroid of its catchment area, and the plotted data are examined to identify any geographic or topographic trends. If a pattern is evident, isolines (lines of equal skew) are drawn and the MSE is computed. The MSE is the mean of the square of the differences between observed skews and isoline skews. If no pattern is evident, an isoline map cannot be developed, and this method is not considered further.
Para desarrollar un mapa de isolíneas de inclinación, cada estación inclinada se plotea en un mapa en el centro de gravedad de su área de la cuenca, y los datos ploteados se examinan para identificar cualquier tendencia geográficas o topográficas. Si un patrón es evidente, las isolíneas (líneas de igual inclinación) se dibujan y el MSE se calcula. El MSE es la media de los cuadrados de las diferencias entre las inclinaciones observadas y las isolíneas inclinadas. Si no hay patrón es evidente, un mapa de isolíneas no puede desarrollarse, y este método no se considera aún más.
In the second method, a prediction equation is used to relate station skew to catchment properties and climatological variables. The MSE is the mean of the square of the differences between observed and predicted skews.
En el segundo método, una ecuación de predicción se utiliza para relacionar la estación de inclinación a las propiedades de la cuenca y variables climatológicas. El MSE es la media de los cuadrados de las diferencias entre las inclinaciones observadas y pronosticadas.
In the third method, the mean and variance of the station skews are calculated. In some cases, the variability of runoff may be such that all the stations may not be hydrologically homogeneous. If this is the case, the values of about 20 stations can be used to calculate the mean and variance of the data.
En el tercer método, la media y la varianza de las inclinaciones de estación se calculan. En algunos casos, la variabilidad de la escorrentía puede ser tal que todas las estaciones pueden no ser hidrológicamente homogénea. Si este es el caso, los valores de alrededor de 20 estaciones se pueden utilizar para calcular la media y la varianza de los datos.
Of the three methods, the one providing the most accurate estimate of skew coefficient is selected. First a comparison of the MSEs from the isolines map and prediction equations is made. Then the smaller MSE is compared to the variance of the data. If the smaller MSE is significantly smaller than the variance, it should be used in Eq. 6-33 as (MSE)sr. If this is not the case, the variance should be used as (MSE)sr, with the mean of the station skews used as regional skew (Csr).
De los tres métodos, se selecciona la que proporciona la estimación más precisa del coeficiente de inclinación. En primer lugar una comparación de las MPE del mapa de isolíneas y se hace ecuaciones de predicción. A continuación, el MSE más pequeño se compara con la varianza de los datos. Si el MSE más pequeño es significativamente menor que la varianza, que debe ser usado en la ecuación. 6-33 como (MSE)sr. Si este no es el caso, la varianza se debe utilizar como (MSE)sr, con la media de la estación de inclinaciones se utiliza como inclinación regional (CSR).
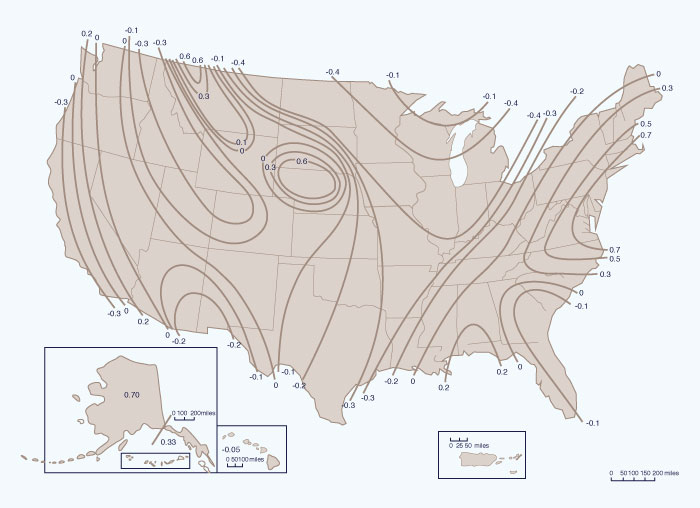
In the absence of regional skew studies, generalized values of regional skew for use in Eq. 6-33 can be obtained from Fig. 6-5. When regional skew is obtained from this figure, the mean square error of the regional skew is MSEsr = 0.302. The mean square error of the station skew is approximated by the following formula:
En ausencia de estudios de inclinación regionales, los valores generalizados de inclinación regional para su uso en la Ec. 6-33 se puede obtener de la Fig. 6-5. Cuando la inclinación regional se obtiene de esta figura, el error cuadrático medio de la inclinación regional es MSEsr = 0.302. El error cuadrático medio de la estación de inclinación se aproxima por la siguiente fórmula:
| (MSE)sy = 10 A - B log (n/10) | (6-34) |
in which
en el cual
| A = - 0.33 + 0.08G, para G < 0.9 | (6-34a) |
| A = 0.52 + 0.30G, para G ≥ 0.9 | (6-34b) |
| B = 0.94 - 0.26G, para G < 1.5 | (6-34c) |
| B = 0.55, for G ≥ 1.5 | (6-34d) |
with G = absolute value of the station skew, and n = record length in years.
con G = valor absolute de la estación de inclinación, y n = historial de longitud en años.
Figure 6-5 Generalized skew coefficient of logarithms of annual maximum streamflow [31] / Coeficiente de inclinación generalizado de logaritmos del caudal máximo anual [31] (Click -here- to display). |
Example 6-5./ Ejemplo 6-5.
A station in San Diego, California, has flood records for 34 y, with station skew Csy = - 0.1.
Calculate a weighted skew following Eq. 6-33 and Fig. 6-5.
Una estación en San Diego, California, cuenta con registros de avenida de 34 años,
con la estación de inclinación Csy = - 0.1. Calcular la siguiente inclinación ponderada Ec. 6-33 y Fig. 6-5.
From Fig. 6-5, the generalized value of regional skew is Csr = -0.3.
The MSE of the station skew is calculated by Eq. 6-34, with G = 0.1: (MSE)sy = 0.156.
Therefore, the weighted skew is (Eq. 6-33):
De la Fig. 6-5, el valor generalizado de la inclinación regional es Csr = -0.3. El MSE de la estación de inclinación se calcula por la Ec. 6-34, con G = 0.1:
(MSE)sy = 0.156.
Por lo tanto, la inclinación ponderada es (Ec. 6-33.):
|
Treatment of Outliers. Outliers are data points that depart significantly from the overall trend of the data. The treatment of these outliers (i.e., their retention, modification, or deletion) may have a significant effect on the value of the statistical parameters computed from the data, particularly for small samples. Procedures for treatment of outliers invariably require judgment involving mathematical and hydrologic considerations.
El tratamiento de los valores extremos. Los valores extremos son los puntos de datos que se apartan significativamente de la tendencia general de los datos. El tratamiento de estos valores extremos (es decir, su retención, modificación o supresión) puede tener un efecto significativo en el valor de los parámetros estadísticos calculados a partir de los datos, en particular para muestras pequeñas. Los procedimientos para el tratamiento de los valores extremos, invariablemente, requieren de un juicio que involucra consideraciones matemáticas e hidrológicos.
The detection and treatment of high and low outliers in the log Pearson III method is performed in the following way [31]. For station skew greater than +0.4, tests for high outliers are considered first. For station skew less than -0.4, tests for low outliers are considered first. For station skew in the range -0.4 to +0.4, tests for high and low outliers are considered simultaneously, without eliminating any outliers from the data.
La detección y el tratamiento de los valores extremos de alta y baja en el método del logaritmo de Pearson III se lleva a cabo de la siguiente manera [31]. Para la estación de inclinación superior a +0.4, las pruebas para altos valores extremos se consideran en primer lugar. Para la estación de inclinación menor que -0.4, las pruebas de valores extremos bajos se consideran en primer lugar. Para la estación de inclinación en el rango de -0.4 a +0.4, las pruebas para los valores extremos altos y bajos se consideran simultáneamente, sin eliminar valores extremos de los datos.
The following equation is used to detect high outliers:
La siguiente ecuación se usa para detectar valores extremos altos:
| yH = ȳ + Kn sy | (6-35) |
in which yH = high outlier threshold (in log units); and Kn = outlier frequency factor, a function of record length n. Values of yH are given in Table A-7 (Appendix A).
en el que yH = límites de valores extremos altos (en unidades logarítmicas); y Kn = factor de frecuencia de valores extremos, una función de la longitud de registro n. Los valores de yH se dan en Tabla A-7 (Apéndice A).
Values of yi (logarithms of the flood series) greater than yH are considered to be high outliers. If there is sufficient evidence to indicate that a high outlier is a maximum in an extended period of time, it is treated as historical data. Otherwise, it is retained as part of the flood series.
Los valores de yi (logaritmos de la serie de avenidas) mayor que yH se consideran altos valores extremos. Si hay evidencia suficiente para indicar que un alto valor extremo es un máximo en un periodo de tiempo prolongado, se trata como datos históricos. De lo contrario, se retiene como parte de la serie de avenida.
Historical data refers to flood information outside of the flood series, which may be used to extend the record to a period much longer than that of the flood series. Historical knowledge is used to define the historical period H, which is longer than the record period n. The number z of events that are known to be the largest in the historical period are given a weight of 1. The remaining n events from the flood series are given a weight of (H - z)/n. For instance, for a record length n = 44 y, a historical period H = 77 y, and a number of peaks in the historical period z = 3, the weight applied to the three historical peaks would be 1, and the weight applied to the remaining flood series would be (77 - 3)/44 = 1.68. In other words, the record is extended to 77 y, and the 44 y of flood series (excluding outliers that have been considered part of the historical data) represent 74 y of data in the historical period of 77 y [31].
Los datos históricos se refiere a la información de avenida fuera de la serie de avenidas, que se puede utilizar para extender el registro a un período mucho más largo que el de la serie de avenida. El conocimiento histórico se utiliza para definir el período histórico H, que es más largo que el período de registro n. El número z de eventos que son conocidos por ser los más grandes en el período histórico se les da un peso de 1. Los n eventos restantes de la serie de avenidas se les da un peso de (H - z)/n. Por ejemplo, para una longitud de registro n = 44 y, un período histórico H = 77 y, y un número de picos en el período histórico z = 3, el peso aplicado a los tres picos históricos sería 1, y el peso aplicado a la serie de avenidas restante sería (77 - 3) / 44 = 1.68. En otras palabras, el registro se amplía a 77 y, y la 44 y de la serie de avenidas (excluyendo los valores extremos que se han considerado parte de los datos históricos) representan 74 y de los datos en el período histórico de 77 y [31].
The following equation is used to detect low outliers:
La siguiente ecuación se utiliza para detectar los valores extremos bajos:
| yL = ȳ - Kn sy | (6-36) |
in which yL = low outlier threshold (in log units) and other terms are as defined previously. If an adjustment for historical data has been previously made, the values on the right-hand side of Eq. 6-36 are those previously used in the historically weighted computation. Values of yi smaller than yL are considered to be low outliers and deleted from the flood series [31].
en el que yL = límite de los valores extremos bajos (en unidades logarítmicas) y otros términos son los definidos previamente. Si un ajuste para los datos históricos se ha hecho anteriormente, los valores en el lado derecho de la Ec. 6-36 son las utilizadas previamente en el cálculo históricamente ponderado. Los valores de yi más pequeños que yL se consideran valores extremos bajos y borrados desde la serie de avenidas [31].
Complements to Flood Frequency Estimates. The accuracy of flood estimates based on frequency analysis deteriorates for values of probability much greater than the record length. This is due to sampling error and to the fact that the underlying distribution is not known with certainty. Alternative procedures that complement the information provided by flood frequency analysis are recommended. These procedures include flood estimates from precipitation data (e.g., unit hydrograph, Chapter 5) and comparison with catchments of similar hydrologic characteristics (regional analysis, Chapter 7). Table 6-4 shows the relationship between the various types of analysis used in flood frequency studies.
Complementos de las estimaciones de frecuencia de avenidas. La precisión de las estimaciones de avenida basado en el análisis de frecuencia se deteriora para valores de probabilidad mucho mayor que la longitud de registro. Esto es debido al error de muestreo y al hecho de que la distribución subyacente no se conoce con certeza. Se recomiendan los procedimientos alternativos que complementan la información proporcionada por el análisis de frecuencia de avenida. Estos procedimientos incluyen las estimaciones de avenida de los datos de precipitación (por ejemplo, hidrograma unitario, Capítulo 5) y comparación con las cuencas de características hidrológicas similares (análisis regional, Capítulo 7). Tabla 6-4 muestra la relación entre los diversos tipos de análisis utilizados en los estudios de frecuencia de avenida.
| |||||||||||||||||||||||
Gumbel's Extreme Value Type I Method / Método de Valor Extremo de Gumbel Tipo I
The extreme value Type I distribution, also known as the Gumbel method [16], or EVl, has been widely used in the United States and other countries. The method is a special case of the three-parameter GEV distribution described in the British Flood Studies Report [23].
La distribución del valor extremo Tipo I, también conocido como el método de Gumbel [16], o EVL, ha sido ampliamente utilizado en los Estados Unidos y otros países. El método es un caso especial de la distribución GEV de tres parámetros descritos en el Reporte de Estudios de Avenida Británico [23].
The cumulative density function F(x) of the Gumbel method is the double exponential, Eq. 6-19, repeated here for convenience:
La función de densidad acumulativa F(x) del método de Gumbel es el doble exponencial, la Ec. 6-19, que se repite aquí por conveniencia:
| F(x) = e -e -y | (6-19) |
in which F(x) is the probability of nonexceedance. In flood frequency analysis, the probability of interest is the probability of exceedance, i.e., the complementary probability to F(x):
en la que F(x) es la probabilidad de no excedencia. En el análisis de frecuencia de avenida, la probabilidad de interés es la probabilidad de excedencia, es decir, la probabilidad complementaria a F(x):
| G(x ) = 1 - F(x ) | (6-37) |
The return period T is the reciprocal of the probability of exceedance. Therefore,
El período de retorno T es el inverso de la probabilidad de excedencia. Por lo tanto,
|
1 _____ = 1 - e -e -y T | (6-38) |
From Eq. 6-38:
De la Ec. 6-38:
|
T y = - ln ln _______ T - 1 | (6-39) |
In the Gumbel method, values of flood discharge are obtained from the frequency formula, Eq. 6-29, repeated here for convenience:
En el método de Gumbel, los valores de descarga de avenida se obtienen de la fórmula de frecuencia, la Ec. 6-29, que se repite aquí por conveniencia:
| x = x̄ + K s | (6-29) |
The frequency factor K is evaluated with the frequency formula:
El factor de frecuencia K se evalúa con la fórmula de frecuencia:
| y = ȳn + K σn | (6-40) |
in which y = Gumbel (reduced) variate, a function of return period (Eq. 6-39); and ȳn and σn are the mean and standard deviation of the Gumbel variate, respectively. These values are a function of record length n (see Table A-8, Appendix A).
en la que y = variable aleatoria de Gumbel (reducido), una función del período de retorno (Ec. 6-39.); y ȳn y σn son la media y la desviación estándar de la variable aleatoria de Gumbel, respectivamente. Estos valores son una función de la longitud de registro n (véase Table A-8, Apéndice A).
In Eq. 6-29, for K = 0, x is equal to the mean annual flood x̄. Likewise, in Eq. 6-40, for K = 0, the Gumbel variate y is equal to its mean ȳn. The limiting value of ȳn, for n → ∞ is the Euler constant, 0.5772 [28]. In Eq. 6-38, for y = 0.5772: T = 2.33 years. Therefore, the return period of 2.33 y is taken as the return period of the mean annual flood.
En la Ec. 6-29, para K = 0, x es igual a la media de la avenida anual x̄. Del mismo modo, en la Ec. 6-40, para K = 0, la variable aleatoria de Gumbel y es igual a media ȳn. El valor límite de ȳn, for n → ∞ es la constante Euler, 0.5772 [28]. En la Ec. 6-38, para y = 0.5772: T = 2.33 años. Por lo tanto, el período de retorno de 2.33 y se toma como el período de retorno de la media de la avenida anual.
From Eqs. 6-29 and 6-40:
A partir de las Ecs. 6-29 y 6-40:
|
y - ȳn x = x̄ + ___________ s σn | (6-41) |
and with Eq. 6-39:
y con la Ec. 6-39:
|
ln ln [T / (T - 1)] + ȳn x = x̄ - __________________________ s σn | (6-42) |
The following steps are necessary to apply the Gumbel method:
Los pasos siguientes son necesarios para aplicar el Metodo de Gumbel:
Assemble the flood series.
Ensamblar la serie de avenidas.
Calculate the mean x̄ and standard deviation s of the flood series.
Calcular las medias x̄ y la desviación estándar s de la serie de avenidas.
Use Table A-8 to determine the mean ȳn and standard deviation σn of the Gumbel variate as a function of record length n.
Utilizar la Tabla A-8 para determinar la media ȳn y la desviación estándar σn de la variable aleatoria de Gumbel como una función de la longitud de registro n.
Select several return periods Tj and associated exceedance probabilities Pj.
Seleccionar varios períodos de retorno Tj y probabilidades de excedencia asociados Pj.
Calculate the Gumbel variates yj corresponding to the return periods Tj by using Eq. 6-39, and calculate the flood discharge Qj = xj for each Gumbel variate (and associated return period) using Eq. 6-41. Alternatively, the flood discharges can be calculated directly for each return period by using Eq. 6-42.
Calcular las variables aleatorias de Gumbel yj correspondientes a los períodos de retorno Tj por medio de la Ec. 6-39, y calcular la descarga de Qj = xj para cada variable aleatoria de Gumbel (y el periodo de retorno asociado) usando la Ec. 6-41. Alternativamente, las descargas de avenida se pueden calcular directamente para cada periodo de retorno mediante el uso de la Ec. 6-42.
Values of Q are plotted against y or T (or P) on Gumbel probability paper, and a straight line is drawn through the points. Gumbel probability paper has an arithmetic scale of Gumbel variate y in the abscissas and an arithmetic scale of flood discharge Q in the ordinates. To facilitate the reading of frequencies and probabilities, Eq. 6-38 may be used to superimpose a scale of return period T (or probability P) on the arithmetic scale of Gumbel variate y.
Los valores de Q se plotean frente y or T (or P) sobre papel de probabilidad de GUmbel, y una línea recta se dibuja a través de los puntos. el papel de probabilidad de Gumbel tiene una escala aritmética de variables aleatorias de Gumbel y en las abscisas y una escala aritmética de la descarga de avenida Q en las ordenadas. Para facilitar la lectura de las frecuencias y probabilidades, la Eq. 6-38 puede utilizarse para superponer una escala de período de retorno T (o probabilidad P) en la escala aritmética de las variables aleatorias de Gumbel y.
Example 6-6.
Apply the Gumbel method to the flood series of Example 6-3.
Plot the results on Gumbel paper along with the plotting positions calculated in Example 6-3.
Aplicar el método de Gumbel a la serie de avenida del Ejemplo 6-3.
Graficar los resultados sobre el papel de Gumbel junto con las posiciones del ploteo
calculados en el Ejemplo 6-3.
The mean and standard deviation of the flood series are: x̄ = 1704 m3/s and s = 795 m3/s. From Table A-8. for n = 16, the mean and standard deviation of the Gumbel variate are ȳ = 0.5157 and σn = 1.0316.
The results are shown in Table 6-5.
Columns 1 and 2 show selected return periods T and associated exceedance probabilities (in percent). Column 3 shows the values of Gumbel variate calculated by Eq. 6-39.
Column 4 shows the flood discharge Q calculated by Eq. 6-41 for each variate y, return period T, and associated exceedance probability P.
The flood discharges define a straight line when plotted versus return period on Gumbel paper, as shown by the solid line of Fig. 6-6. Plotting positions calculated by Example 6-3 are shown for comparison purposes.
La media y la desviación estándar de las series de avenida son:
x̄ = 1704 m3/s and s = 795 m3/s.
A partir de la Tabla A-8. para n = 16, la media y la desviación estándar de la variable aleatoria de Gumbel son ȳ = 0.5157 and σn = 1.0316.
Los resultados se muestran en la Tabla 6-5.
Las Columnas 1 y 2 muestran períodos de retorno seleccionados T y las probabilidades de excedencia asociados (en porcentaje).
La Columna 3 muestra los valores de la variable aleatoria Gumbel calculado por la Ec. 6-39.
La Columna 4 muestra la descarga de avenida Q calculado por la Ec. 6-41 para cada variable aleatoria y, período de retorno T, y la probabilidad de excedencia asociada
P.
Las descargas de avenida define una línea recta cuando se representa gráficamente frente al período de retorno en el papel de Gumbel, como se muestra por la línea continua de la Fig. 6-6.
Representando gráficamente las posiciones calculadas en el Ejemplo 6-3 se muestran para propósitos de comparación.
ONLINE CALCULATION. Using ONLINE GUMBEL,
the results are essentially the same, varying from Q = 447 m3/s for T = 1.05 y, to Q = 5396 m3/s for T = 200 y.
CÁLCULO EN LÍNEA. Usando ONLINE GUMBEL, los resultados son esencialmente el mismo,
variando de Q = 447 m3/s para T = 1.05 y, a Q = 5396 m3/s para T = 200 y.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Figure 6-6 Flood frequency analysis by Gumbel method: Example 6-6. / Análisis de la frecuencia de avenida por el Método de Gumbel: Ejemplo 6-6. |
Modifications to the Gumbel Method. Since its inception in the 1940s, several modifications to the Gumbel method have been proposed. Gringorten [12] has shown that the Gumbel distribution does not follow the Weibull plotting rule, Eq. 6- 26 (or Eq. 6-27 with a = 0). He recommended a = 0.44, which led to the Gringorten plotting position formula:
Las modificaciones al método de Gumbel. Desde sus inicios en la década de 1940, se han propuesto varias modificaciones en el método de Gumbel. Gringorten [12] ha demostrado que la distribución de Gumbel no sigue la regla de trazado de Weibull, la Ec. 6- 26 (o la Ec. 6-27 con a = 0). Se recomienda a = 0.44, lo que llevó a la fórmula de posición del trazado de Gringorten:
|
1 m - 0.44 ____ = P = _______________ T n + 0.12 | (6-43) |
Lettenmaier and Burges [22] have suggested that better flood estimates are obtained by using the limiting values of mean and standard deviation of the Gumbel
variate (i.e., those corresponding to
Lettenmaier y Burges [22] han sugerido que una mejor estimación de la avenida se obtienen mediante el uso de los valores límite de la media y la desviación estándar de la variable aleatoria de Gumbel (es decir, los correspondientes a
| x = x̄ + (0.78 y - 0.45) s | (6-44) |
and Eq. 6-42 reduces to
y la Ec. 6-42 se reduce a
|
T x = x̄ + (0.78 ln ln _______ + 0.45) s T - 1 | (6-45) |
Lettenmaier and Burges [22] have also suggested that a biased variance estimate, using n as the divisor in Eq. 6-3, yields better estimates of extreme events that the usual unbiased estimate, that is, the divisor n - 1.
Lettenmaier y Burges [22] también han sugerido que una estimación de la varianza parcial, usando n como el divisor en la Ec. 6-3, proporciona mejores cálculos de los eventos extremos que la estimación no parcial de costumbre, es decir, el divisor n - 1.
Comparison Between Flood Frequency Methods
Comparación entre los Métodos de Frecuencia de Avenida
In 1966, the Hydrology Subcommittee of the U.S. Water Resources Council began work on selecting a suitable method of flood frequency analysis that could be recommended for general use in the United States.
En 1966, el Subcomité de Hidrología del Consejo de Recursos Hídricos de EE.UU. comenzó a trabajar en la selección de un método adecuado de análisis de frecuencia de avenida que podrían recomendarse para uso general en los Estados Unidos.
The committee tested the goodness of fit of six distributions: (1) lognormal, (2) log Pearson III, (3) Hazen, (4) gamma, (5) Gumbel (EV1) and (6) log Gumbel (EV2). The study included ten sets of records, the shortest of which was 40 y. The findings showed that the first three distributions had smaller average deviations that the last three. Since the Hazen distribution is a type of lognormal distribution and the lognormal is a special case of the log Pearson III, the Committee concluded that the latter was the most appropriate of the three, and hence recommended it for general use.
El comité puso a prueba la bondad de ajuste de seis distribuciones: (1) logaritmo normal, (2) logaritmo de Pearson III, (3) Hazen, (4) gamma, (5) Gumbel (EV1) y (6) logaritmo de Gumbel (EV2). El estudio incluyó a diez conjuntos de registros, el menor de los cuales era 40 años. Los resultados mostraron que las tres primeras distribuciones tenían desviaciones medias más pequeñas que las tres últimas. Dado que la distribución de Hazen es un tipo de distribución logarítmica normal y el logaritmo normal es un caso especial del logaritmo de Pearson III, el Comité llegó a la conclusión de que este último era el más apropiado de los tres, y por lo tanto se recomienda para el uso general.
The same type of analysis was repeated for six sets of records in the United Kingdom, the shortest of which was 32 y [2]. The methods were: (1) gamma, (2) log gamma, (3) lognormal, (4) Gumbel (EV1), (5) GEV, (6) Pearson Type III, and (7) log Pearson III. At low return periods (from 2 to 5 y), the GEV and Pearson Type III showed the smallest average deviations, whereas for return periods exceeding 10 y the log Pearson III method had the smallest average deviations.
El mismo tipo de análisis se repitió para los seis conjuntos de registros en el Reino Unido, el menor de los cuales era 32 y [2]. Los métodos fueron: (1) gamma, (2) logaritmo gamma, (3) logaritmo normal, (4) Gumbel (EV1), (5) GEV, (6) Tipo de Pearson III, y logaritmo de Pearson III. En períodos de retorno bajos (del 2 al 5 y), el GEV y Tipo Pearson III mostraron las desviaciones medias más pequeños, mientras que para los períodos de retorno superiores a 10 y el método del logaritmo de Pearson III tenía las desviaciones medias más pequeñas.
Similar comparative studies were reported in the British Flood Studies Report [23]. The study concluded that the three-parameter distributions (GEV, Pearson Type III, and log Pearson III) provided a better fit than the two-parameter distributions (Gumbel, lognormal, gamma, log gamma). Based on mean absolute deviation criteria, the study rated the log Pearson III method better than the GEV and the latter better than the Pearson Type III. However, based on root mean square deviation, it rated the Pearson Type III better than both the log Pearson III and GEV distributions.
Se informaron estudios comparativos similares en el Reporte de Estudios de Avenida Británico [23]. El estudio concluyó que las distribuciones de tres parámetros (GEV, Pearson Tipo III, y logaritmo de Pearson III) proporcionan un mejor ajuste de las distribuciones de dos parámetros (Gumbel, logaritmo normal, gamma, y logaritmo gamma). Sobre la base de criterios absolutos de la desviación media, el estudio tiene el método de logaritmo de Pearson III mejor que el GEV y los segundos mejor que Pearson Tipo III. Sin embargo, basado en la raíz de la desviación cuadrática media, es calificado como Pearson Tipo III mejor que ambas distribuciones el logaritmo Pearson III y GEV.
Although in general, the three-parameter methods seemed to fare better than the two-parameter methods, the latter should not be completely discarded. The British Flood Studies Report [23] observed that their use in connection with short record lengths often leads to results which are more sensible than those obtained by fitting three-parameter distributions. A three-parameter distribution fitted to a small sample may in some cases imply that there is an upper bound to the flood discharge equal to about twice the mean annual flood. While there may be an upper limit to flood magnitude, it is certainly higher than twice the mean annual flood.
Aunque, en general, los métodos de tres parámetros parecieron pasarlo mejor que los métodos de dos parámetros, este último no debe ser completamente descartada. El Reporte de los Estudios de Avenida Británico [23] observó que su uso en conexión con longitudes de registro cortos a menudo conduce a resultados que son más sensibles que los obtenidos por las distribuciones de tres parámetros de ajuste. Una distribución de tres parámetros montado en una muestra pequeña puede en algunos casos implica que exista un límite superior a la descarga de avenida igual a aproximadamente el doble de la avenida anual media. Si bien puede haber un límite superior a la magnitud de las avenidas, sin duda es mayor que el doble de la avenida anual media.
6.3 FRECUENCIA DE FLUJO BAJO
|
|
Whereas high flows lead to floods, sustained low flows can lead to droughts. A drought is defined as a lack of rainfall so great and continuing so long as to affect the plant and animal life of a region adversely and to deplete domestic and industrial water supplies, especially in those regions where rainfall is normally sufficient for such purposes [18].
Mientras que los flujos altos conducen a avenidas, los flujos bajos sostenidos pueden dar lugar a sequías. Una sequía se define como la falta de lluvias tan grande y continua, siempre que pueda afectar a la vida animal y vegetal de una región de manera adversa y para agotar los suministros de agua doméstica e industrial, especialmente en aquellas regiones donde la lluvia es normalmente suficiente para tales fines [18 ].
In practice, a drought refers to a period of unusually low water supplies, regardless of the water demand. The regions most subject to droughts are those with the greatest variability in annual rainfall. Studies have shown that regions where the variance coefficient of annual rainfall exceeds 0.35 are more likely to have frequent droughts [6]. Low annual rainfall and high annual rainfall variability are typical of arid and semiarid regions. Therefore, these regions are more likely to be prone to droughts.
En la práctica, una sequía se refiere a un período de suministros inusualmente bajos de agua, independientemente de la demanda de agua. Las regiones más afectadas por la sequía son los que tienen mayor variabilidad en las precipitaciones anuales. Los estudios han demostrado que las regiones donde el coeficiente de varianza de la precipitación anual excede 0.35 son más propensos a tener frecuentes sequías [6]. La variabilidad de la precipitación anual baja y la precipitación anual alta son típicas de las regiones áridas y semiáridas. Por lo tanto, estas regiones son más propensas a ser propensos a las sequías.
Studies of tree rings, which document long term trends of rainfall, show clear patterns of periods of wet and dry weather [30]. While there is no apparent explanation for the cycles of wet and dry weather, the dry years must be considered in planning water resource projects. Analysis of long records has shown that there is a tendency for dry years to group together. This indicates that the sequence of dry years is not random, with dry years tending to follow other dry years. It is therefore necessary to consider both the severity and duration of a drought period.
Los estudios de anillos de los árboles, que documentan las tendencias a largo plazo de las precipitaciones, muestran patrones claros de períodos de clima húmedo y seco [30]. Si bien no hay una explicación evidente para los ciclos de clima húmedo y seco, los años secos se deben considerar en la planificación de proyectos de recursos hídricos. El análisis de los registros de tiempo ha demostrado que existe una tendencia a que los años secos se agrupen. Esto indica que la secuencia de años secos no es al azar, con los años secos tienden a seguir a otros años secos. Por tanto, es necesario tener en cuenta tanto la severidad y la duración de un período de sequía.
The severity of droughts can be established by measuring:
The deficiency in rainfall and runoff,
The decline of soil moisture, and/or
The decrease in groundwater levels.
La severidad de las sequías se puede establecer mediante la medición:
La deficiencia en la precipitación y escorrentía,
La disminución de la humedad del suelo, y/o
La disminución de los niveles de agua subterránea.
Alternatively, low-flow-frequency analysis can be used in the assessment of the probability of occurrence of droughts of different durations.
Por otra parte, el análisis de frecuencia de flujo bajo se puede utilizar en la evaluación de la probabilidad de ocurrencia de sequías de diferentes duraciones.
Figure 6-7 Curvas de Frecuencia de Flujo Bajo [28]. |
Methods of low-flow frequency analysis are based on an assumption of invariance of meteorological conditions. The absence of long records, however, imposes a stringent limitation on low-flow frequency analysis. When records of sufficient length are available, analysis begins with the identification of the low-flow series. Either the annual minima or the annual exceedance series are used. In a monthly analysis, the annual minima series is formed by the lowest monthly flow volumes in each year of record. If the annual exceedance method is chosen, the lowest monthly flow volumes in the record are selected, regardless of when they occurred. In the latter method, the number of values in the series need not be equal to the number of years of record.
Los métodos de análisis de frecuencia de flujo bajo se basan en la hipótesis de invariancia de las condiciones meteorológicas. La ausencia de registros de tiempo, sin embargo, impone una limitación estricta en el análisis de frecuencia de bajo flujo. Cuando los registros de suficiente longitud están disponibles, el análisis comienza con la identificación de la serie de bajo flujo. O bien se utilizan los mínimos anuales o la serie de excedencia anual. En un análisis mensual, las serie mínima anual está formada por los volúmenes de los flujos mensuales más bajos de cada año de registro. Si se elige el método de excedencia anual, los volúmenes de flujo mensual más baja en el registro se seleccionan, independientemente del momento en que ocurrieron. En el último método, el número de valores en la serie no tiene que ser igual al número de años de registro.
A flow duration curve can be used to give an indication of the severity of low flows. Such a curve, however, does not contain information on the sequence of low flows or the duration of possible droughts. The analysis is made more meaningful by abstracting the minimum flows over a period of several consecutive days. For instance, for each year, the 7-day period with minimum flow volume is abstracted, and the minimum flow is the average flow rate for that period. A frequency analysis on the low-flow series, using the Gumbel method, for instance, results in a function describing the probability of occurrence of low flows of a certain duration. The same analysis repeated for other durations leads to a family of curves depicting low-flow frequency, as shown in Fig. 6-7 [28].
Una curva de duración de flujo puede ser usado para dar una indicación de la severidad de flujos bajos. Tal curva, sin embargo, no contiene información sobre la secuencia de los flujos bajos o la duración de posibles sequías. El análisis se hace más significativa mediante la abstracción de los flujos mínimos durante un período de varios días consecutivos. Por ejemplo, para cada año, el período de 7 días con un volumen de flujo mínimo se abstrae, y el flujo mínimo es la velocidad del flujo promedio para ese período. Un análisis de frecuencia en la serie de bajo flujo, utilizando el método de Gumbel, por ejemplo, resulta en una función que describe la probabilidad de ocurrencia de los bajos flujos de una cierta duración. El mismo análisis repetido para otras duraciones conduce a una familia de curvas que representan la frecuencia de bajo flujo, como se muestra en la Fig. 6-7 [28].
In reservoir design, the assessment of low flows is aided by a flow-mass curve. The technique involves the determination of storage volumes required for all low-flow periods. Although it is practically impossible to provide sufficient storage to meet hydrologic risks of great rarity, common practice is to provide for a stated risk (i.e., a drought probability) and to add a suitable percent of the computed storage volume as reserve storage allowance. The variance coefficient of annual flows is used in determining the risk and storage allowance levels. Extraordinary drought levels are then met by cutting draft rates.
En el diseño del reservorio, la evaluación de flujos bajos es ayuda por una curva de flujo de masa. La técnica consiste en la determinación de los volúmenes de almacenamiento necesarios para todos los períodos de bajo flujo. A pesar de que es prácticamente imposible para proporcionar almacenamiento suficiente para satisfacer los riesgos hidrológicos de gran rareza, una práctica común consiste en prever un riesgo indicado (es decir, una probabilidad de sequía) y añadir un porcentaje adecuado del volumen de almacenamiento calculado como margen de almacenamiento de reserva. El coeficiente de variación de los flujos anuales se utiliza en la determinación de los niveles de riesgo y tolerancia de almacenamiento. Los iveles de sequía extraordinarias se reunieron a continuación mediante la reducción de las tasas de los proyectos.
Regulated rivers may alter natural flow conditions to provide a minimum downstream flow for specific purposes. In this case, the reservoirs serve as the mechanism to diffuse the natural flow variability into downstream flows which can be made to be nearly constant in time. Regulation is necessary for downstream low-flow maintenance, usually for the purpose of meeting agricultural, municipal and industrial water demands, minimum instream flows, navigation draft, and water pollution control regulations.
Ríos regulados pueden alterar las condiciones de flujo natural para proporcionar un flujo aguas abajo mínimo para fines específicos. En este caso, los reservorios sirven como el mecanismo para difundir la variabilidad del flujo natural en los flujos de aguas abajo que se pueden hacer para ser casi constante en el tiempo. La regulación es necesaria para el mantenimiento de bajo flujo aguas abajo, por lo general con el propósito de cumplir con las demandas de agua para la agricultura, municipal e industrial, de los flujos ecológicos mínimos, proyecto de navegación, y las regulaciones de control de la contaminación del agua.
6.4 SEQUÍAS
|
|
Drought is a weather-related natural phenomenon, affecting regions of the Earth for months or years. It has an impact on food production, reducing life expectancy and the economic performance of large geographic regions or entire countries.
La sequía es un fenómeno natural relacionado con el clima, que afecta a las regiones de la Tierra durante meses o años. Tiene un impacto en la producción de alimentos, la reducción de la esperanza de vida y el rendimiento económico de las grandes regiones geográficas o países enteros.
Drought is a recurrent feature of the climate; it occurs in virtually all climatic zones, with its characteristics varying significantly among regions. Drought differs from aridity in that drought is temporary; aridity is a permanent characteristic of regions with low rainfall.
La sequía es un rasgo recurrente del clima; se produce en zonas prácticamente todas climáticas, con sus características variando significativamente entre las regiones. La sequía difiere de la aridez en que la sequía es temporal; aridez es una característica permanente de regiones con escasez de precipitaciones.
Drought is related to a deficiency of precipitation over an extended period of time, usually for a season or more (Fig. 6-8). This deficiency results in a water shortage for some activity, group, or environmental sector. Drought is also related to the timing of precipitation. Other climatic factors such as high temperature, high wind, and low relative humidity are often associated with drought.
La sequía está relacionada con una deficiencia de precipitación durante un período prolongado de tiempo, por lo general para una temporada o más (Fig. 6-8). Esta deficiencia da lugar a una escasez de agua para alguna actividad, grupo o sector ambiental. La sequía también está relacionada con el tiempo de precipitación. Otros factores climáticos tales como alta temperatura, viento fuerte, y la baja humedad relativa están a menudo asociados con la sequía.
Drought is more than a physical phenomenon or natural event. Its impact results from the relation between a natural event and the demands on the water supply, and it is often exacerbated by human activities. The experience from droughts has underscored the vulnerability of human societies to this natural hazard.
La sequía es más que un fenómeno físico o evento natural. Su impacto resulta de la relación entre un evento natural y las demandas en el suministro de agua, y que a menudo se ve agravada por las actividades humanas. La experiencia de las sequías ha puesto de relieve la vulnerabilidad de las sociedades humanas a este peligro natural.
Figure 6-8 Backlands in Rio Grande do Norte, in the drought-stricken Brazilian Northeast./ |
Definition of drought
Drought definitions are of two types: (1) conceptual, and (2) operational. Conceptual definitions help understand the meaning of drought and its effects. For example, drought is a protracted period of precipitation deficiency which causes extensive damage to crops, resulting in loss of yield.
Las definiciones de sequía son de dos tipos: (1) conceptuales, y (2) en funcionamiento. Definiciones conceptuales ayudan a entender el significado de la sequía y sus efectos. Por ejemplo, la sequía es un período prolongado de deficiencia de precipitación que causa grandes daños a los cultivos, lo que resulta en la pérdida de rendimiento.
Operational definitions help identify the drought's beginning, end, and degree of severity. To determine the beginning of drought, operational definitions specify the degree of departure from the precipitation average over some time period. This is usually accomplished by comparing the current situation (the study period) with the historical average. The threshold identified as the beginning of a drought (e.g., 75% of average precipitation over a specified time period) is usually established somewhat arbitrarily.
Las definiciones operacionales ayudan a identificar el principio de la sequía, el final y el grado de severidad. Para determinar el inicio de la sequía, las definiciones operacionales especifican el grado de desviación de la media de la precipitación sobre un cierto período de tiempo. Esto generalmente se logra mediante la comparación de la situación actual (el período de estudio) con el promedio histórico. El umbral identificado como el comienzo de una sequía (por ejemplo, 75% de la precipitación media durante un período de tiempo especificado) generalmente se establece un tanto arbitraria.
An operational definition for agriculture may compare daily precipitation to evapotranspiration to determine the rate of soil-moisture depletion, and express these relationships in terms of drought effects on plant behavior. Operational definitions are used to analyze drought frequency, severity, and duration for a given historical period. Such definitions, however, require weather data on hourly, daily, monthly, or other time scales and, possibly, impact data (e.g., crop yield). A climatology of drought for a given region provides a greater understanding of its characteristics and the probability of recurrence at various levels of severity. Information of this type is beneficial in the formulation of mitigation strategies.
Una definición operativa para la agricultura puede comparar la precipitación diaria y la evapotranspiración para determinar la tasa de humedad del suelo el agotamiento, y expresar estas relaciones en términos de los efectos de la sequía sobre el comportamiento de las plantas. Las definiciones operacionales se utilizan para analizar la frecuencia de las sequías, la gravedad y la duración de un período histórico dado. Tales definiciones, sin embargo, requieren datos meteorológicos por hora, día, mes, u otras escalas de tiempo y, posiblemente, los datos de impacto (por ejemplo, el rendimiento del cultivo). Una climatología de la sequía para una región determinada proporciona una mayor comprensión de sus características y la probabilidad de recurrencia en los distintos niveles de severidad. Este tipo de información es beneficiosa en la formulación de estrategias de mitigación.
Types of droughts
The following types of drought have been identified:
Los siguientes tipos de sequía se han identificado:
- Meteorological drought,
Sequía metereológica,
- Agricultural drought,
Sequía agrícola,
- Hydrological drought, and
Sequía hidrológica, y
- Socieoeconomic drought.
Sequía socioeconómica.
Meteorological drought is defined on the basis of the degree of dryness, in comparison to a normal or average amount, and the duration of the dry period. Definitions of meteorological drought must be region-specific, since the atmospheric conditions that result in deficiencies of precipitation are highly variable.
La sequía meteorológica se define sobre la base del grado de sequedad, en comparación con una cantidad normal o promedio, y la duración del período seco. Las definiciones de sequía meteorológica deben ser específicos de la región, ya que el las condiciones atmosféricas que resultan en deficiencias de precipitación son altamente variables.
The variety of meteorological definitions in different countries illustrates why it is not possible to apply a definition of drought developed in one part of the world to another. For instance, the following definitions of drought have been reported:
La variedad de definiciones meteorológicas en diferentes países ilustra por qué no es posible aplicar una definición de sequía desarrollado en una parte del mundo a otra. Por ejemplo, se han notificado las siguientes definiciones de sequía:
United States (1942): Less than 2.5 mm of rainfall in 48 hours.
Estados Unidos (1942): Menos de 2.5 mm de lluvia en 48 horas.
Great Britain (1936): Fifteen consecutive days with daily precipitation less than 0.25 mm.
Gran Bretaña (1936): Quince días consecutivos con precipitación diaria de menos de 0.25 mm.
Libya (1964): When annual rainfall is less than 180 mm.
Libia (1964): Cuando la precipitación anual es inferior a 180 mm.
Bali (1964): A period of six days without rain.
Bali (1964): Un período de seis días sin lluvia.
Data sets required to assess meteorological drought are: (1) daily rainfall, (2) temperature, (3) humidity, (4) wind velocity, and (5) evaporation.
Los conjuntos de datos necesarios para evaluar la sequía meteorológica son: (1) la precipitación diaria, (2) la temperatura, (3) la humedad, (4) la velocidad del viento, y (5) la evaporación.
Agricultural drought links various characteristics of meteorological drought to agricultural impacts, focusing on precipitation shortages, differences between actual and potential evapotranspiration, soil-water deficits, reduced groundwater or reservoir levels, and so on. Plant water demand depends on prevailing weather conditions, biological characteristics of the specific plant, its stage of growth, and the physical and biological properties of the soil. A good definition of agricultural drought should account for the susceptibility of crops during different stages of crop development. Deficient topsoil moisture at planting may hinder germination, leading to low plant populations per hectare and a reduction of yield.
La sequía agrícola enlaza diversas características de la sequía meteorológica a los efectos agrícolas, se centra en la escasez de precipitaciones, las diferencias entre la evapotranspiración real y potencial, déficit de agua del suelo, reducen los niveles de agua subterránea o de depósito, y así sucesivamente. La demanda de agua de la planta depende de las condiciones climáticas imperantes, las características biológicas de la planta específica, su etapa de crecimiento, y las propiedades físicas y biológicas del suelo. Una buena definición de la agricultura la sequía debe tener en cuenta la susceptibilidad de los cultivos durante las diferentes etapas de desarrollo del cultivo. Deficiencia de humedad en la capa superior del suelo de la plantación puede impedir la germinación, que conduce a bajas poblaciones de plantas por hectárea y una reducción del rendimiento.
Data sets required to assess agricultural drought are: (1) soil texture, (2) soil fertility, (3) soil moisture, (4) crop type and area, (5) crop water requirements, (6) pests, and (7) climate.
Los conjuntos de datos necesarios para evaluar la sequía agrícola son: (1) textura del suelo, (2) la fertilidad del suelo, (3) la humedad del suelo, (4) el tipo de cultivo y el área, (5) las necesidades de agua del cultivo, (6) las plagas, y (7 ) el clima.
Hydrological drought refers to a persistently low discharge and/or volume of water in streams and reservoirs, lasting months or years. Hydrological drought is a natural phenomenon, but it may be exacerbated by human activities. Hydrological droughts are usually related to meteorological droughts, and their recurrence interval varies accordingly. Changes in land use and land degradation can affect the magnitude and frequency of hydrological droughts.
La sequía hidrológica se refiere a una persistente descarga baja y/o volumen de agua en arroyos y reservorios, que duran meses o años. La sequía hidrológica es un fenómeno natural, pero puede ser exacerbada por las actividades humanas. Las sequías hidrológicas son por lo general relacionados a las sequías meteorológicas, y su intervalo de recurrencia varía en consecuencia. Los cambios en el uso del suelo y la degradación del suelo pueden afectar a la magnitud y frecuencia de las sequías hidrológicas.
Data sets required to assess hydrological drought are: (1) surface-water area and volume, (2) surface runoff, (3) streamflow measurements, (4) infiltration, (5) water-table fluctuations, and (6) aquifer properties.
Los conjuntos de datos necesarios para evaluar la sequía hidrológica son: (1) área y volumen del agua de superficial, (2) la escorrentía superficial, (3) las mediciones de caudal (4) la infiltración, (5) las fluctuaciones del nivel freático, y (6) las propiedades del acuífero.
Socioeconomic drought associates the supply and demand of some economic good with elements of meteorological, hydrological, and agricultural drought. It differs from the other types of drought in that its occurrence depends on the processes of supply and demand. The supply of many economic goods, such as water, forage, food grains, fish, and hydroelectric power, depends on the weather. Due to the natural variability of climate, water supply is ample in some years but insufficient to meet human and environmental needs in other years.
La sequía socioeconómica asocia la oferta y la demanda de algún bien económico con elementos de la meteorología, hidrología y sequía agrícola. Se diferencia de los otros tipos de la sequía en que su aparición depende de los procesos de la oferta y la demanda. El suministro de muchos bienes económicos, como el agua, forraje, cereales, pescado, y la energía hidroeléctrica, depende el clima. Debido a la variabilidad natural del clima, el suministro de agua es abundante en algunos años, pero insuficiente para satisfacer las necesidades humanas y ambientales en otros años.
Socioeconomic drought occurs when the demand for an economic good exceeds the supply as a result of a weather-related shortfall in water supply. The drought may result in significantly reduced hydroelectric power production because power plants were dependent on streamflow rather than storage for power generation. Reducing hydroelectric power production may require the government to convert to more expensive petroleum alternatives and to commit to stringent energy conservation measures to meet its power needs.
La sequía socioeconómica se produce cuando la demanda de un bien económico excede a la oferta como resultado de un déficit relacionado con el clima en suministro de agua. La sequía puede dar como resultado una disminución significativa de la producción de energía hidroeléctrica porque las centrales eran dependientes del caudal en lugar del almacenamiento para la generación de energía. La reducción de la producción de energía hidroeléctrica puede requerir al gobierno para convertir a las alternativas más caras de petróleo y comprometerse a estrictas medidas de conservación de energía para satisfacer sus necesidades de energía.
The demand for economic goods is increasing as a result of population growth and economic development. The supply may also increase because of improved production efficiency, technology, or the construction of reservoirs. When both supply and demand increase, the critical factor is their relative rate of change. Socioeconomic drought is promoted when the demand for water for economic activities far exceeds the supply.
La demanda de bienes económicos está aumentando como consecuencia del crecimiento demográfico y el desarrollo económico. La alimentación también puede aumentar debido a la mejora de la eficiencia de producción, la tecnología, o la construcción de reservorios. Cuando la oferta y la demanda aumentan, el factor crítico es la tasa relativa de cambio. La sequía socioeconómica se promueve cuando la demanda de agua para actividades económicas es muy superior a la oferta.
Data sets required to assess socioeconomic drought are: (1) human and animal population, (2) growth rate, (3) water and fodder requirements, (4) severity of crop failure, and (5) industry type and water requirements.
Los conjuntos de datos necesarios para evaluar la sequía socioeconómica son: (1) la población humana y animal, (2) la tasa de crecimiento, (3) las necesidades de agua y forraje, (4) severidad de la pérdida de cosechas, y (5) tipo de industria y requerimientos de agua.
Intensity-Duration-Frequency Relations / Relaciones Frecuencia-Duración-Intensidad
The relations between intensity, duration, and frequency of droughts may be analyzed by the conceptual model described in Table 6-6 [27]. The conceptual approach is applicable to meteorological droughts lasting at least one year, in midlatitudinal regions where the prevailing climate may be primarily characterized by precipitation.
Las relaciones entre la intensidad, duración y frecuencia de las sequías pueden ser analizada por el modelo conceptual descrita en la Tabla 6-6 [27]. El enfoque conceptual es aplicable a las sequías meteorológicas que duran por lo menos un año, en las regiones de latitudes medias donde el clima predominante puede estar caracterizado principalmente por precipitación.
The climate types, from superarid to superhumid, are defined in terms of mean annual precipitation Pma (mm) as shown in Table 6-6, Line 1:
Los tipos de clima, desde super árido a super húmedo, se definen en términos de la precipitación media anual Pma(mm) como se muestra en la Tabla 6-6, Línea 1:
|
The (mean) annual global terrestrial precipitation is Pagt = 800 mm [27]. At the extremes of the climatic spectrum, mean annual precipitation is less than 100 mm (superarid), or greater than 6400 mm (superhumid). The superarid example is the Atacama desert, in northern Chile, with mean annual precipitation Pma = 0.5 mm, which is hardly measurable. The superhumid example is Cherrapunji, in Meghalaya, Eastern India, with mean annual precipitation Pma = 11,777 mm, long considered by many as the wettest spot on Earth. However, Mawsynran, near Cherrapunji, now boasts Pma = 11,873 mm, effectively edging out Cherrapunji of the distinction.
La precipitación terrestre global (media) anual es Pagt = 800 mm [27]. En los extremos del espectro climático, la precipitación media anual es inferior a 100 mm (super árido), o mayor que 6400 mm (super húmedo). El ejemplo super árido es el desierto de Atacama, en el norte de Chile, con una precipitación media anual Pma = 0.5 mm, que no es medible. El ejemplo super húmedo es Cherrapunji, en Meghalaya, al Este de la India, con una precipitación media anual Pma = 11,777 mm, siempre considerado por muchos como el punto más húmedo de la Tierra. Sin embargo, Mawsynran, cerca de Cherrapunji, ahora cuenta con Pma = 11,873 mm, efectivamente superando a Cherrapunji de la distinción.
*****1609131450***
Climates types may also be defined as the ratio of mean annual precipitation Pma to (mean) annual global terrestrial precipitation Pagt (Line 2). The ratio Pma/Pagt = 1 depicts the middle of the climatic spectrum.
Los tipos de climas también pueden definirse como la relación entre la precipitación media anual Pma a la precipitación terrestre global (media) anual Pagt (Línea 2). La relación de Pma/Pagt = 1 representa la media del espectro climático.
The conceptual model is also defined in terms of the annual potential evaporation (evapotranspiration) Eap (Line 3) and of the ratio of annual potential evaporation to mean annual precipitation Eap/Pma (Line 4). The ratio Eap/Pma = 2 describes the middle of the climatic spectrum. To complement the description, the length of the rainy season Lrs is also indicated (Line 5).
El modelo conceptual también se define en términos de la evaporación potencial anual (evapotranspiración) Eap (Línea 3) y de la relación de la evaporación potencial anual a la precipitación media anual Eap/Pma (Línea 4). La relación Eap/Pma = 2 describe la mitad del espectro climático. Para complementar la descripción, la longitud de la temporada de lluvias Lrs también se indica (Línea 5).
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
For any year for which P is the annual precipitation, drought intensity I
is defined as the ratio of the deficit (Pma - P) to the
mean (Pma). For any year, an intensity I = 0.25 is classified as moderate;
Para cualquier año para el que P es la precipitación anual, la intensidad de la sequía I
se define como la proporción del déficit (Pma - P) para la
media (Pma). Para cualquier año, una intensidad
I = 0.25 se clasifica como moderada;
Experience has shown that the longer droughts generally occur around the middle of the climatic spectrum (800 mm of mean annual precipitation). Drought duration varies between 1 yr (or less) at the extremes of the climatic spectrum and (about) 6 yr around the middle (Line 9) [26]. Droughts lasting more than 6 yr are uncommon; they are more likely to be driven by anthropogenic pressures, for instance, deforestation or overgrazing [25]. A classical example of an anthropogenically derived drought is that of the Sahel, in Northern Africa (Fig. 6-9), where, in the past 40 years, droughts have had a tendency to persist for durations much longer than normal.
La experiencia ha demostrado que las sequías más largas generalmente se producen alrededor de la mitad del espectro climático (800 mm de precipitación media anual). La duración de sequía varía entre 1 año (o menos) en los extremos del espectro climático y (sobre) 6 yr alrededor de la mitad (Línea 9) [26]. Las sequías que duran más de 6 años son poco comunes; son más probables que sean impulsadas por las presiones antropogénicas, por ejemplo, la deforestación o pastoreo excesivo [25]. Un ejemplo clásico de una sequía antropogénicamente derivada es la del Sahel, en &AACUTE;frica del Norte (Fig. 6-9), donde, en los últimos 40 años, las sequías han tenido una tendencia a persistir durante períodos mucho más largos de lo normal.
Figure 6-10 shows values of standardized annual seasonal rainfall (June-October) in the Sahel for the period 1898-2004. The standardized annual rainfall has zero mean and unit standard deviation. Note that through the 1980s, drought in the Sahel persisted for more than 10 years.
La figura 6-10 muestra los valores de la precipitación anual normalizado estacional (Junio-Octubre) en el Sahel para el período 1898-2004. La precipitación anual estandarizada tiene una media cero y una desviación estándar unitaria. Tenga en cuenta que a través de la década de 1980, la sequía en el Sahel persistió durante más de 10 años.
|
Figure 6-9 Mean annual precipitation in the Sahel, North Africa./ Precipitación anual media en el Sahel, África del Norte.
Figure 6-10 Standardized annual rainfall in the Sahel for the period 1898-2004./ La precipitación anual estandarizada en el Sahel para el período de 1898-2004. |
In general, the dry periods (drought events) are followed by corresponding wet periods. Therefore, the drought recurrence interval (i.e., the reciprocal of the frequency) is always greater than the drought duration. Drought recurrence intervals increase from 2 year on the extreme dry side of the climatic spectrum (superarid) to (more than) 100 years on the extreme wet side (superhumid) (Line 10, Table 6-6).
En general, los períodos secos (eventos de sequía) son seguidos por períodos húmedos correspondientes. Por lo tanto, el intervalo de recurrencia de las sequías (es decir, el recíproco de la frecuencia) es siempre mayor que la duración de sequía. Los intervalos de recurrencia de la sequía aumentará de 2 años en el lado extremo seco del espectro climático (superárido) a (más de) 100 años en el lado extremo húmedo (superhúmedo) (Línea 10, Tabla 6-6).
PREGUNTAS
|
|
In statistical analysis, what are the measures of central tendency? Explain.
En el análisis estadístico, ¿cuáles son las medidas de tendencia central? Explicar.
What is skewness? A distribution with a long tail on the right side has positive or negative skewness?
¿Qué es la asimetría? Una distribución que tenga una larga cola en el lado derecho tiene asimetría positiva o negativa?
What are the parameters of the gamma distribution? How are the gamma and Pearson Type III distributions related?
¿Cuáles son los parámetros de la distribución gamma? ¿Cómo están relacionadas las distribuciones gamma y Pearson Tipo III?
What is the parameter that distinguishes the three extreme value distributions? What is the limiting value of the mean of the Gumbel variate?
¿Cuál es el parámetro que distingue a las tres distribuciones de valores extremos? ¿Cuál es el valor límite de la media de la variable aleatoria de Gumbel?
What is the difference between the annual exceedance series and the annual maxima series? What is risk in the context of frequency analysis?
¿Cuál es la diferencia entre la serie anual de excedencia y la serie de máximos anuales? ¿Qué es el riesgo en el contexto del análisis de frecuencia?
How is an extreme value probability paper constructed? What type of probability paper is used in the log Pearson Type III method?
¿Cómo se construye un papel de probabilidad de valores extremos? ¿Qué tipo de papel de probabilidad se utiliza en el método de logaritmo de Pearson Tipo III?
What is the difference between the Weibull, Blom, and Gringorten plotting position formulas?
¿Cuál es la diferencia entre las fórmulas de posición de Weibull, Blom y el graficador de Gringorten?
How is skewness variability accounted for in the log Pearson III method?
¿Cómo es la variabilidad asimétrica en cuenta en el método del logaritmo de Pearson III?
When are high outliers considered part of historical data? When is it necessary to perform a historically weighted computation?
¿Cuándo están altos los valores atípicos considerados parte de los datos históricos? ¿Cuándo es necesario realizar un cálculo ponderado históricamente?
Why are two-parameter distributions such as the Gumbel distribution appropiate for use in connection with short record lengths?
¿Por qué son las distribuciones de dos parámetros, tales como la distribución de Gumbel apropiada para su uso en conexión con longitudes de registro cortos?
Compare floods and droughts from the standpoint of frequency analysis.
Comparar las avenidas y sequías desde el punto de vista del análisis de frecuencia.
What is the mean annual precipitation in the middle of the climatic spectrum?
¿Cuál es la precipitación media anual en el centro del espectro climático?
What is the mean annual potential evaporation in the middle of the climatic spectrum?
¿Cuál es la evaporación potencial media anual en la mitad del espectro climático?
Why are the droughts in the Sahel likely to persist much longer than normal?
¿Por qué las sequías en el Sahel son probables que persistan mucho más tiempo de lo normal?
PROBLEMAS
|
|
Develop a spread sheet to calculate the mean, standard deviation, and skew coefficient of a series of annual maximum flows. Test your work using the data of Example 6-1 in the text.
Desarrollar una hoja de cálculo para calcular la media, la desviación estándar y el coeficiente de asimetría de una serie de caudales máximos anuales. Probar el cálculo utilizando los datos del Ejemplo 6-1 en el texto.
The annual maximum flows of a certain stream have been found to be normally distributed with mean 22,500 ft3/s and standard deviation 7500 ft3/s. Calculate the probability that a flow larger than 39,000 ft3/s will occur.
Se han encontrado los flujos máximos anuales de un determinado flujo que se distribuye normalmente con una media de 22,500 ft3/s y desviación estándar de 7500 ft3/s. Calcular la probabilidad de que un flujo mayor de 39,000 ft3/s ocurrirá.
The 10-y and 25-y floods of a certain stream are 73 and 84 m3/s, respectively. Assuming a normal distribution, calculate the 50-y and 100-y floods.
Las avenidas de 10-y y 25-y de una determinada corriente son 73 y 84 m3/s, respectivamente. Suponiendo una distribución normal, calcular las avenidas de 50-y y 100-y.
The low flows of a certain stream have been shown to follow a normal distribution. The flows expected to be exceeded 95% and 90% of the time are 15 and 21 m3/s, respectively. What flow can be expected to be exceeded 80% of the time?
Los flujos bajos de cierta corriente se ha demostrado que siguen una distribución normal. Los flujos esperados que exceden el 95% y el 90% de las veces son 15 y 21 m3/s, respectivamente. ¿Qué flujo se espera que exceda 80% del tiempo?
A temporary cofferdam for a 5-y dam construction period is designed to pass the 25-y flood. What is the risk that the cofferdam may fail before the end of the construction period? What design return period is needed to reduce the risk to less than 10%?
Una ataguía temporal por un período de construcción de la presa 5-y está diseñado para pasar la avenida de 25-y. ¿Cuál es el riesgo de que la ataguía pueda fallar antes de que finalice el período de construcción? ¿Qué período de retorno de diseño es necesaria para reducir el riesgo a menos del 10%?
Use the Weibull formula (Eq. 6-26) to calculate the plotting positions for the following series of annual maxima, in cubic feet per second: 1305, 3250, 4735, 5210, 4210, 2120, 2830, 3585, 7205, 1930, 2520, 3250, 5105, 4830, 2020, 2530, 3825, 3500, 2970, 1215.
Use la fórmula de Weibull (Ec. 6-26.) para calcular las posiciones de trazado para la siguiente serie de máximos anuales, en pies cúbicos por segundo: 1305, 3250, 4735, 5210, 4210, 2120, 2830, 3585, 7205, 1930, 2520, 3250, 5105, 4830, 2020, 2530, 3825, 3500, 2970, 1215.
Use the Gringorten formula to calculate the plotting positions for the following series of annual maxima, in cubic meters per second: 160, 350, 275, 482, 530, 390, 283, 195, 408, 307, 625, 513.
Utilice la fórmula de Gringorten para calcular las posiciones graficadas para la siguiente serie de máximos anuales, en metros cúbicos por segundo: 160, 350, 275, 482, 530, 390, 283, 195, 408, 307, 625, 513.
Modify the spread sheet of Problem 6-1 to calculate the mean, standard deviation, and skew coefficients of the logarithms of a series of annual maximum flows. Test your work using the results of Example 6-4 in the text.
Modificar la hoja de cálculo del Problema 6-1 para calcular la media, la desviación estándar y coeficientes de inclinación de los logaritmos de una serie de flujos máximos anuales. Probar el cálculo utilizando los resultados del Ejemplo 6-4 en el texto.
Fit a log Pearson III curve to the data of Problem 6-6. Plot the calculated distribution on log probability paper, along with the Weibull plotting positions calculated in Problem 6-6.
Ajustar una curva del logaritmo de Pearson III para los datos del Problema 6-6. Representar gráficamente la distribución calculada en el papel logarítmico de probabilidad, junto con las posiciones gráficas de Weibull calculadas en el Problema 6-6.
Fit a Gumbel curve to the data of Problem 6-6. Plot the calculated distribution on Gumbel paper, along with the Weibull plotting positions calculated in Problem 6-6.
Ajustar una curva de Gumbel a los datos del Problema 6-6. Representar gráficamente la distribución calculada en papel de Gumbel, junto con las posiciones gráficas de Weibull calculadas en el Problema 6-6.
Develop a spread sheet to read a series of annual maxima, sort the data in descending order, and compute the corresponding plotting positions (percent chance and return period) by the Weibull and Gringorten formulas.
Desarrollar una hoja de cálculo para leer una serie de máximos anuales, ordenar los datos en orden descendente, y calcular las posiciones gráficas correspondientes (por ciento de posibilidades y período de retorno) por las fórmulas de Weibull y Gringorten.
Given the following statistics of annual maxima for stream X: number of years n = 35;
mean = 3545 ft3/s ; standard deviation = 1870 ft3/s. Compute the 100-y flood by the Gumbel method.Teniendo en cuenta las siguientes estadísticas de máximos anuales para el flujo X: número de años n = 35;
media = 3545 ft3/s ; desviación estándar = 1870 ft3/s. Calcular la avenida de 100-y por el método de Gumbel.Given the following statistics of annual maxima for river Y: number of years n = 45;
mean = 2700 m3/s ; standard deviation 1300 m3/s; mean of the logarithms = 3.1; standard deviation of the logarithms = 0.4; skew coefficient of the logarithms = - 0.35. Compute the 100-y flood using the following probability distributions: (a) normal, (b) Gumbel, and (c) log Pearson III.Teniendo en cuenta las siguientes estadísticas de máximos anuales para el río Y: número de años n = 45;
media = 2700 m3/s ; desviación estándar 1300 m 3/s; media de los logaritmo s = 3.1; desviación estándar de los logaritmos = 0,4; coeficiente de asimetría de los logaritmos = - 0.35. Calcular la avenida de 100-y usando las siguientes distribuciones de probabilidad: (a) normal, (b) Gumbel, y (c) Logaritmo de Pearson III.A station near Denver, Colorado, has flood records for 48 y, with station skew
Csy = - 0.18. Calculate a weighted skew coefficient.Una estación cerca de Denver, Colorado, tiene los registros de avenidas de 48 años, con la estación de inclinación
Csy = - 0.18 Calcular un coeficiente de inclinación ponderado.Determine if the value Q = 13,800 ft3/s is a high outlier in a 45-y flood series with the following statistics: mean of the logarithms = 3.572; standard deviation of the logarithms = 0.215.
Determinar si el valor Q = 13,800 pies3/s es un alto valor atípico en una serie de avenidas de 45-y con las siguientes estadísticas: media de los logaritmos = 3.572; desviación estándar de los logaritmos = 0,215.
Using the Lettenmaier and Burges modification to the Gumbel method, fit a Gumbel curve to the data of Example 6-6 in the text. Plot the calculated distribution on Gumbel paper, along with plotting positions calculated by the Gringorten formula.
El uso de la modificación Lettenmaier y Burges con el método de Gumbel, ajustar una curva Gumbel a los datos del ejemplo 6-6 en el texto. Representar gráficamente la distribución calculada en papel de Gumbel, junto con posiciones gráficas calculadas por la fórmula Gringorten.
BIBLIOGRAFÍA
|
|
Benson, M. A. (1962). "Plotting Positions and Economics of Engineering Planning," Journal of the Hydraulics Division, ASCE, Vol. 88, Noviembre, pp. 57-71.
Benson, M. A. (1968). "Uniform Flood Frequency Estimating Methods for Federal Agencies," Water Resources Research, Vol. 4, pp. 891-908.
Blom, G. (1958). Statistical Estimates and Transformed Beta Variables. New York: John Wiley.
Casella, G., and R. L. Berger. (1990). Statistical Inference, Wadsworth & Brooks/Cole, Pacific Grove, California.
Chow, V. T. (1951). "A General Formula for Hydrologic Frequency Analysis," Transactions, American Geophysical Union, Vol. 32, pp. 231-237.
Chow, V. T. (1964). Handbook of Applied Hydrology. Nueva York: McGraw-Hill.
Cunnane, C. (1978). "Unbiased Plotting Positions-A Review," Journal of Hydrology, Vol. 37, pp. 205-222.
Fisher, R. A., and L. H. C. Tippett. (1928). "Limiting Forms of a Frequency Distribution of the Smallest and Largest Member of a Sample," Proceedings, Cambridge Philosophical Society, Vol. 24, pp.180-190.
Foster, H. A. (1924). "Theoretical Frequency Curves and their Application to Engineering Problems," Transactions, ASCE, Vol. 87, pp. 142-173.
Frechet, M. (1927). "Sur la loi de Probabilite de l'ecart Maximum," (On the Probability Law of Maximum Error), Annals of the Polish Mathematical Society, (Cracow), Vol. 6, pp. 93-116.
Fuller, W. E. (1914). "Flood Flows," Transactions, ASCE, Vol. 77, pp. 564-617.
Gringorten, 1.1. (1963). "A Plotting Rule for Extreme Probability Paper," Journal of Geophysical Research, Vol. 68, No.3, February, pp. 813-814.
Gumbel, E. J. (1941). "Probability Interpretation of the Observed Return Periods of Floods," Transactions, American Geophysical Union, Vol. 21, pp. 836-850.
Gumbel, E. J. (1942). "Statistical Control Curves for Flood Discharges," Transactions, American Geophysical Union, Vol. 23, pp. 489-500.
K Gumbel , E. J. (1943). "On the Plotting of Flood Discharges," Transactions, American Geophysical Union, Vol. 24, pp. 699-719.
Gumbel, E. J. (1958). Statistics of Extremes. Irvington, N.Y.: Columbia University Press.
Hazen, A. (1914). Discussion on "Flood Flows," by W. E. Fuller, Transactions, ASCE, Vol. 77, p. 628.
Havens, A. V. (1954). "Drought and Agriculture," Weatherwise, Vol. 7, pp. 51-55.
Horton, R. E. (1913). "Frequency of Recurrence of Hudson River Floods," U.S. Weather Bureau Bulletin Z, pp. 109-112.
Jenkinson, A. F. (1955). "The Frequency Distributions of the Annual Maximum (or Minimum) Values of Meteorological Elements," Quarterly Journal of the Royal Meteorological Society, Vol. 87, p. 158.
Kite, G. W. (1977). Frequency and Risk Analyses in Hydrology. Fort Collins, Colorado: Water Resources Publications.
Lettenmaier, D. P., y S. J. Burges. (1982). "Gumbel's Extreme Value Distribution: A New Look," Journal of the Hydraulics Division, ASCE, Vol. 108, No. HY4, Abril, pp. 503-514.
Natural Environment Research Council. (1975). Flood Studies Report. Vol. 1 (of 5 volumes), London, England.
Pearson, K. (1930). "Tables for Statisticians and Biometricians," Part I, 3d. Ed. , The Biometric Laboratory, University College. London: Cambridge University Press.
Ponce, V. M., A. K. Lohani, and P. T. Huston. (1997). "Surface albedo and water resources: Hydroclimatological impact of human activities." Journal of Hydrologic Engineering, ASCE, Vol. 2, No. 4, October, 197-203.
Ponce, V. M., R. P. Pandey, y S. Ercan. (1999). "A conceptual model of drought characterization across the climatic spectrum." Revista de Estudos Ambientais, Vol. 1, No. 3, septiembre-diciembre, 68-76.
Ponce, V. M., R. P. Pandey, y S. Ercan. (2000). "Characterization of drought across climatic spectrum." Journal of Hydrologic Engineering, ASCE, Vol. 5, No. 2, Abril, 222-224.
Riggs, H. C. (1972). "Low-Flow Investigations," Techniques of Water Resources Investigations of the United States Geological Survey, Book 4, Chapter B1.
Spiegel, M. Mathematical Handbook of Formulas and Tables. Schaum's Outline Series in Mathematics. New York: McGraw-Hill.
Troxell, H. C. (1937). "Water Resources of Southern California with Special Reference to the Drought of 1944-51," U.S. Geological Survey Water Supply Paper No. 1366.
U.S. Interagency Advisory Committee on Water Data, Hydrology Subcommittee. (1983). "Guidelines for Determining Flood Flow Frequency," Bulletin No. 17B, issued 1981, revised 1983, Reston, Virginia.
Lecturas sugeridas
Gumbel, E. J. (1958). Statistics of Extremes. Irvington, N.Y.: Columbia University Press.
Natural Environment Research Council. (1975). Flood Studies Report, in 5 volumes, London, England.
Riggs, H. C. (1972). "Low-Flow Investigations," Techniques of Water Resources Investigations of the United States Geological Survey, Book 4, Chapter B1.
U.S. Interagency Advisory Committee on Water Data, Hydrology Subcommittee. (1983). "Guidelines for Determining Flood Flow Frequency," Bulletin No. 17B, issued 1981, revised 1983, Reston, Virginia.
| http://engineeringhydrology.sdsu.edu |
|
160914 00:00 |