|
|
|
CAPÍTULO 7: ANÁLISIS REGIONAL |
|
"In most natural systems, drainage from the uplands finds its way into rivers and then into the ocean. Ocean disposal is nature's way of moving dissolved salts out of the landscape." Jan van Schilfgaarde (1990) |
|
This chapter is divided into three sections. Section 7.1 describes joint probability distributions, including marginal distributions and conditional probability. Section 7.2 describes the techniques of regression analysis. Section 7.3 presents selected techniques for regional analysis of flood and rainfall characteristics. Este capítulo se divide en tres secciones. Sección 7.1 describe las distribuciones de probabilidad conjuntas, incluyendo las distribuciones marginales y de probabilidad condicional. La Sección 7.2 se describen las técnicas de análisis de regresión. La Sección 7.3 presenta las técnicas seleccionadas para el análisis regional de las características de las inundaciones y la lluvia. |
7.1 PROBABILIDAD CONJUNTA
|
|
In engineering hydrology, regional analysis encompasses the study of hydrologic phenomena with the aim of developing mathematical relations to be used in a regional context. Generally, mathematical relations are developed so that information from gaged or long-record catchments can be readily transferred to neighboring ungaged or short-record catchments of similar hydrologic characteristics. Other applications of regional analysis include regression techniques used to develop empirical (i.e., parametric) equations applicable within a broad geographical region. Regional analysis makes use of statistics and probability, including frequency analysis (Chapter 6) and joint probability distributions.
En la ingeniería hidrológica, el análisis regional abarca el estudio de los fenómenos hidrológicos con el objetivo de desarrollar relaciones matemáticas para ser utilizado en un contexto regional. En general, las relaciones matemáticas se desarrollan de manera que la información de cuencas clausuradas o de largo récord se puede transferir fácilmente a las cuencas de captación no aforadas o de corto récord de características hidrológicas similares. Otras aplicaciones del análisis regional incluyen técnicas de regresión utilizados para el desarrollo de ecuaciones empíricas (es decir, paramétrico) aplicables en una amplia región geográfica. El análisis regional hace uso de la estadística y probabilidad, incluyendo análisis de frecuencias (Capítulo 6) y las distribuciones de probabilidad conjunta.
Joint Probability Distributions / Distribuciones de Propabilidad Conjunta
Probability distributions possessing one random variable (X) were discussed in Chapter 6. These are called univariate distributions. Probability distributions with two random variables, X and Y, are called bivariate or joint distributions. A joint distribution expresses in mathematical terms the probability of occurrence of an outcome consisting of a pair of values of X and Y. In statistical notation, P(X = xi, Y = yj) is the probability P that the random variables X and Y will take on the outcomes xi and yj simultaneously. A shorter notation is P(xi, yj).
Las distribuciones de probabilidad que poseen una variable aleatoria (X) se discutieron en el Capítulo 6. Estos se llaman distribuciones univariantes. Las distribuciones de probabilidad con dos variables aleatorias, X y y, se llaman bivariado o distribuciones conjuntas. Una distribución conjunta se expresa en términos matemáticos la probabilidad de ocurrencia de un resultado que consiste en un par de valores de X y Y. En la notación estadística, p(X = xi, Y = yj) es la probabilidad de P que las variables aleatorias X y Y se enfrentará a los resultados xi y yj simultáneamente. Una notación más corta es P(xi, yj).
For xi (1, 2, ... , n), and yj (1, 2, ... , m), the sum of the probabilities of all possible outcomes is equal to unity:
Para xi (1, 2, ..., n) y yj (1, 2, ..., m), la suma de las probabilidades de todos los resultados posibles es igual a la unidad:
|
n m Σ Σ P(xi, yj) = 1 i = 1 j = 1 | (7-1) |
A classical example of joint probability is that of the outcome of the cast of two dice, say A and B. Intuitively, the probability of getting a 1 for A and a 1 for B is P(A = 1, B = 1) = 1/36; see Fig. 7-1. In total, there are 6 × 6 = 36 possible outcomes, and each one of them has the same probability: 1/36 (assuming, of course, that the dice are not loaded). This distribution is referred to as the bivariate uniform distribution because each outcome has a uniform and equal probability of occurrence. The sum of the probabilities of all possible outcomes is confirmed to be equal to 1.
Un ejemplo clásico de probabilidad conjunta es el de los resultados de lanzar dos dados, por ejemplo A y B. Intuitivamente, la probabilidad de obtener un 1 para A y 1 para B es P(A = 1, B = 1) = 1/36; véase la fig. 7-1. En total, hay 6 × 6 = 36 resultados posibles, y cada uno de ellos tiene la misma probabilidad: 1/36 (suponiendo, por supuesto, que los dados no están cargados). Esta distribución se conoce como la distribución uniforme bivariado, ya que cada resultado tiene una probabilidad de ocurrencia uniforme e igual. La suma de las probabilidades de todos los resultados posibles se confirma que es igual a 1.
Figure 7-1 Joint probability: The outcome of two dice. / Probabilidad conjunta: El resultado de dos dados. |
Joint cumulative probabilities are defined in a similar way as for univariate probabilities:
Las probabilidades acumuladas conjuntas se definen de una manera similar como para las probabilidades univariadas:
|
k l F(xk, yl) = Σ Σ P(xi, yj) i = 1 j = 1 | (7-2) |
in which F(xk, yl) is the joint cumulative probability. Continuing with the example of the two dice, the probability of A being ≤ 3 and B being ≤ 3 is the sum of all the individual probabilities, for all combinations of i and j, as i varies from 1 to 3, and as j varies from 1 to 3; i.e., 3 × 3 = 9 possible combinations, resulting in a probability equal to 9 × (1/36) = 1/4.
en el que F(xk, y
Marginal Probability Distributions / Distribuciones de Probabilidad Marginales
Marginal probability distributions are obtained by summing up P(xi, yj) over all values of one of the variables, for instance, X. The resulting (marginal) distribution is the probability distribution of the other variable, in this case Y without regard to X. Marginal distributions are univariate distributions obtained from bivariate distributions. In statistical notation, the marginal probability distribution of X is:
Distribuciones de probabilidad marginales se obtienen mediante la suma de P(xi, yj ) sobre todos los valores de una de las variables, por ejemplo, X. La distribución (marginal) resultante es la distribución de probabilidad de la otra variable, en este caso Y sin tener en cuenta X. Las distribuciones marginales son distribuciones univariantes obtenidas de distribuciones bivariadas. En la notación estadística, la distribución de probabilidad marginal de X es:
|
m P(xi) = Σ P(xi, yj) j = 1 | (7-3) |
Likewise, the marginal distribution of Y is:
Del mismo modo, la distribución marginal de Y es:
|
n P(yj) = Σ P(xi, yj) i = 1 | (7-4) |
The example of the two dice A and B may be used to illustrate the concept of marginal probability. Intuitively, the probability of A being equal to 1, regardless of the value of B, is 6 × (1/36) = 1/6. Likewise, the probability of B being equal to 4, regardless of the value of A, is also 1/6. Notice that the joint probabilities (1/36) of each one of all 6 possible outcomes have been summed in order to calculate the marginal probability.
El ejemplo de los dos dados A y B se puede utilizar para ilustrar el concepto de probabilidad marginal. Intuitivamente, la probabilidad de A es igual a 1, sin importar el valor de B, es 6 × (1/36) = 1/6. Del mismo modo, la probabilidad de B es igual a 4, independientemente del valor de A, también es 1/6. Observe que las probabilidades conjuntas (1/36) de cada uno de los 6 posibles resultados se han resumido con el fin de calcular la probabilidad marginal.
Marginal cumulative probability distributions are obtained by combining the concepts of marginal and cumulative distributions. In statistical notation, the marginal cumulative probability distribution of X is:
Las distribuciones de probabilidad acumulativas marginales se obtienen mediante la combinación de los conceptos de distribuciones marginales y acumulativos. En la notación estadística, la distribución de probabilidad acumulativa marginal de X es:
|
k m F(xk) = Σ Σ P(xi, yj) i = 1 j = 1 | (7-5) |
Likewise, the marginal distribution of Y is:
Del mismo modo, la distribución marginal de Y es:
|
n l F(yl) = Σ Σ P(xi, yj) i = 1 j = 1 | (7-6) |
The example of the two dice A and B is again used to illustrate the concept of marginal cumulative probability. The probability of A ≤ 2, regardless of the value of B, is: 2 × 6 × (1/36) = 1/3. Likewise, the probability of B ≤ 5, regardless of the value of A, is: 5 × 6 × (1/36) = 5/6. To calculate the marginal cumulative probabilities, the concepts of marginal and cumulative distributions have been combined.
El ejemplo de los dos dados A y B se utiliza de nuevo para ilustrar el concepto de probabilidad acumulada marginal. La probabilidad de A ≤ 2, independientemente del valor de B, es: 2 × 6 × (1/36) = 1/3. Del mismo modo, la probabilidad de B ≤ 5, sin tener en cuenta el valor de A, es: 5 × 6 × (1/36) = 5/6. Para el cálculo de las probabilidades acumuladas marginales, los conceptos de distribuciones marginales y acumulativos se han combinado.
Conditional Probability
La probabilidad condicional
The concept of conditional probability is useful in regression analysis and other hydrologic applications. The conditional probability is the ratio of joint and marginal probabilities. In statistical notation:
El concepto de probabilidad condicional es útil en el análisis de regresión y otras aplicaciones hidrológicas. La probabilidad condicional es el cociente de probabilidades conjuntas y marginales. En la notación estadística:
|
P(x,y) P(x |y) = ________ P(y) | (7-7) |
in which P(x |y) is the conditional probability of x, given y. Likewise, the conditional probability of y, given x, is:
en el que P(x | y) es la probabilidad condicional de x, dado y. Del mismo modo, dada la probabilidad condicional de y, x, es:
|
P(x,y) P(y |x) = ________ P(x) | (7-8) |
From Eqs. 7-7 and 7-8, it follows that joint probability is the product of conditional and marginal probabilities.
A partir de las ecuaciones 7-7 y 7-8, se deduce que la probabilidad conjunta es el producto de las probabilidades condicionales y marginales.
Joint probability distributions can be expressed as continuous functions.
In this case they are called joint density functions, with the notation f(x,y).
For the conditional density function, the notation is
Las distribuciones de probabilidad conjunta se pueden expresar como funciones continuas.
En este caso se les llama funciones de densidad conjunta, con la notación f(x,y).
Para la función de densidad condicional, la notación es
As with univariate distributions, the moments provide descriptions of the properties of joint distributions. For continuous functions, the joint moment of order r and s about the origin (indicated with ') is defined as follows:
Al igual que con las distribuciones univariantes, los momentos proporcionan descripciones de las propiedades de las distribuciones de conjuntos. Para las funciones continuas, el momento conjunto de orden r y s sobre el origen (indicado con ') se define de la siguiente manera:
|
∞ ∞ μ'r,s = ∫ ∫ x ry s f (x,y ) dy dx -∞ -∞ | (7-9) |
With r = 1 and s = 0, Eq. 7-9 reduces to the mean of x :
Con r = 1 y s = 0, la Ec. 7-9 se reduce a la media de x :
|
∞ ∞ μ'1,0 = ∫ x [ ∫ x ry s f (x,y ) dy ] dx -∞ -∞ | (7-10) |
with the expression between brackets being the marginal PDF of x, or f(x). Therefore, the expression for the mean of x is:
con la expresión entre parésntesis es el PDF marginal de x o f(x). Por lo tanto, la expresión para la media de x es:
|
∞ μ'1,0 = μx = ∫ x f (x ) dx -∞ | (7-11) |
Similar equations hold for y.
Las ecuaciones similares son válidas para y.
The second moments are usually written about the mean:
Los segundos momentos se escriben normalmente sobre la media:
|
∞ ∞ μ'r,s = ∫ ∫ ( x - μx )r ( y - μy )s f (x,y ) dy dx -∞ -∞ | (7-12) |
For r = 2 and s = 0, Eq. 7-12 reduces to the variance of x.
Likewise, for r = 0 and s = 2, Eq. 7-12 reduces to the variance of y.
A third type of second moment, i.e., the covariance, arises for r = 1 and
Para r = 2 y s = 0, la Ec. 7-12 reduce a la diferencia de x.
Del mismo modo, para r = 0 y s = 2, la Ec 7-12 se reduce a la diferencia de y.
Un tercer tipo de segundo momento, es decir, la covarianza, surge para r = 1 y
|
∞ ∞ σx,y = ∫ ∫ ( x - μx ) ( y - μy ) f (x, y ) dy dx -∞ -∞ | (7-13) |
in which σx,y is the covariance.
en la que σ x,y es la covarianza.
The correlation coefficient is a dimensionless value relating the covariance σx,y and standard deviations σx and σy :
El coeficiente de correlación es un valor adimensional que relaciona la covarianza σx,y y las desviaciones estándar σ x y σ y :
|
σx,y ρx,y = _________ σx σy | (7-14) |
in which ρx,y is the correlation coefficient based on population data. The sample correlation coefficient is:
en la que ρx,y es el coeficiente de correlación basados en los datos de población. El coeficiente de correlación de la muestra es:
|
sx,y rx,y = ________ sx sy | (7-15) |
The calculation of sample correlation coefficient rx,y including the sample covariance sx,y is illustrated by Example 7-1.
The correlation coefficient is a measure of the linear dependence between x and y.
It varies in the range of -1 to + 1.
A value of ρ (or r ) close to or equal to 1 indicates a strong linear dependence
between the variables, with large values of x associated with large values of y,
and small values of x with small values of y.
A value of ρ (or r ) close to or equal to -1 indicates a correlation such that large values of x are associated with small values of y and vice versa.
A value of ρ = 0
El cálculo del coeficiente de correlación de la muestra rx,y
incluyendo la covarianza de la muestra sx,y se ilustra con el ejemplo 7-1.
El coeficiente de correlación es una medida de la dependencia lineal entre xyy.
Esto varía en el intervalo de -1 a + 1.
Un valor de ρ (or) cerca de o igual a 1 indica una fuerte dependencia lineal entre las variables,
con grandes valores de x asociados con grandes valores de y,
y pequeños valores de x con pequeños valores de y.
Un valor de ρ (o r) cerca de o igual a -1 indica una correlación tal que grandes valores de x se asocian con valores pequeños de y y vice versa.
Un valor de ρ = 0
Example 7-1. / Ejemplo 7-1.
The monthly flows of the North Fork and South Fork tributaries of a certain stream (see, for example, Fig. 7-2) have the following joint probability distribution f (x, y) (expressed as mean value in each class) (Note that
1 hm3 = 1 million cubic meters):
Los flujos mensuales de los afluentes de North Fork y South Fork de cierta corriente (véase,
por ejemplo, la Fig. 7-2) tienen la siguiente distribución de probabilidad conjunta
f(x, y) (expresado como valor medio en cada clase) (Nótese que 1 hm3 = 1 millón de metros cúbicos):
Calculate the marginal distributions, means, variances, standard deviations, covariance, and correlation coefficient for this joint distribution.
Calcular las distribuciones marginales, medios, varianzas, desviaciones estándar, la covarianza y el coeficiente de correlación para esta distribución conjunta.
The North Fork marginal distribution, f(x), is obtained by summing up the joint probabilities across y.
Therefore:
La distribución marginal de North Fork, f(x), se obtiene resumiendo las probabilidades conjuntas a través de y.
Por consiguiente:
Likewise, the South Fork marginal distribution, f(y), is obtained by summing up the joint probabilities across x:
Del mismo modo, la distribución marginal de South Fork, f(y), se obtiene
resumiendo las probabilidades conjuntas a través de x:
The means are the first moments of the marginal distributions with respect to the origin:
Los medios son los primeros momentos de las distribuciones marginales con respecto al origen:
The variances are the second moments of the marginal distributions with respect to the means:
Las varianzas son los segundos momentos de las distribuciones marginales con respecto a los medios:
sx2 = Σ ( x - x̄ )2 f (x) Therefore:
Por consiguiente:
sx = 95.26 hm3
Likewise, for y:
Asimismo, para y:
sy = 97.42 hm3
The covariance is the second moment of the joint distribution:
La covarianza es el segundo momento de la distribución conjunta:
The correlation coefficient is rx,y = sx,y / (sx sy) = 7785 / (95.26 × 97.42) = 0.839.
El coeficiente de correlación es rx,y = sx,y / (sx sy) = 7785 / (95.26 × 97.42) = 0.839.
ONLINE CALCULATION. Using
ONLINE TWOD CORRELATION,
the answer
is: Correlation coefficient rx,y = 0.839, confirming the hand calculation.
CÁLCULO EN LÍNEA. Usando
ONLINE TWOD CORRELATION,
la respuesta es: coeficiente de correlaciónrx,y = 0.839, confirmando
el cálculo manual.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
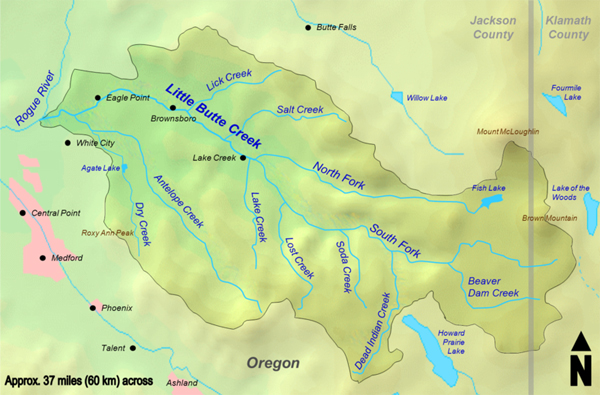
|
Figure 7-2 North Fork and South Fork, Little Butte Creek, Oregon. / North Fork and South Fork, Little Butte Creek, Oregon.
Bivariate Normal Distribution
Distribución normal bivariado
Among the many joint probability distributions, the bivariate normal distribution is important in hydrology because itis the foundation of regression theory. The bivariate normal probability distribution is [12]:
Entre las muchas distribuciones de probabilidad conjunta, la distribución normal bivariada es importante en la hidrología porque es el fundamento de la teoría de la regresión. La distribución de probabilidad normal bivariada es [12]:
| f (x , y) = K e M | (7-16) |
in which x and y are the random variables, and K and M are coefficient and exponent. respectively, defined as follows:
en el que x y y son las variables aleatorias, y K y M son coeficiente y exponente, respectivamente, que se define como sigue:
|
1 K = _________________________ 2 π σx σy (1 - ρ2)1/2 | (7-17) |
|
1 M = - ___________ [ A ] 2 (1 - ρ2) | (7-18a) |
in which:
en el cual:
|
x - μx x - μx y - μy y - μy A = ( _________ )2 - 2 ρ ( _________ ) ( _________ ) + ( _________ )2 σx σx σy σy | (7-18b) |
The distribution has five parameters: the means μx and μy, the standard deviations σx and σy, and the correlation coefficient ρ.
La distribución tiene cinco parámetros: los medios μx y μy, las desviaciones estándar σx y σ y, y el coeficiente de correlación ρ.
Following Eq. 7-8, the conditional distribution is obtained by dividing the bivariate normal (Eq. 7-16) by the univariate normal (Eq. 6-7), to yield
Después de la Ec. 7-8, la distribución condicional se obtiene dividiendo el bivariante normal (Ec. 7-16) por el univariado normal (Ec. 6-7), para producir
|
f
(x, y) K = _________ = K' eM' f (x) | (7-19) |
in which K' and M' are coefficient and exponent, respectively, defined as follows:
en el que K' y M' son coeficiente y exponente, respectivamente, que se define de la siguiente manera:
|
1 K' = _____________________ σy [2 π (1 - ρ2)]1/2 | (7-20) |
|
1
σy M' = - ________________ [ (y - μy) - ρ ______ (x - μx) ]2 2 σy2 (1 - ρ2) σx | (7-21) |
By inspection of Eqs. 7-20 and 7-21, and comparison with Eq. 6-7, it is concluded that the conditional distribution is also normal, with mean and variance:
Por inspección de las Ecs. 7-20 y 7-21, y la comparación con la Ec. 6-7, se concluye que la distribución condicional también es normal, con media y la varianza:
|
σy μy|x = μy - ρ _____ (x - μx) σx | (7-22) |
| σe2 = σy2 (1 - ρ2) | (7-23) |
Equations 7-22 and 7-23 are useful in regression analysis. Equation 7-22 expresses the linear dependence between x and y. The slope of the regression line is [ρ σy/σx]. Likewise, ρ is the fraction of the original variance explained or removed by the regression. In other words, the variance of the conditional distribution is less than or equal to the variance of y without regard to x, and it depends on the value of the correlation coefficient ρ. For ρ = 1, all the variance is removed, and the error of the predictive equation (i.e., the error of the regression) is reduced to zero. For ρ = 0, none of the original variance is removed, and σe remains equal to σy.
Las ecuaciones 7-22 y 7-23 son útiles en el análisis de regresión. La ecuación 7-22 expresa la dependencia lineal entre el x e y. La pendiente de la línea de regresión es [ρ σ y/σx]. Del mismo modo, ρ es la fracción de la varianza inicial explicado o eliminado por la regresión. En otras palabras, la varianza de la distribución condicional es menor que o igual a la varianza de y sin tener en cuenta x, y depende del valor del coeficiente de correlación ρ. Para ρ = 1, toda la varianza se retira, y el error de la ecuación de predicción (es decir, el error de la regresión) se reduce a cero. Para ρ = 0, no se elimina nada de la varianza original, y σe se mantiene igual a σy.
7.2 ANÁLISIS DE REGRESIÓN
|
|
A fundamental tool of regional analysis is the equation relating two or more hydrologic variables. The variable for which values are given is called the predictor variable. The variable for which values must be estimated is called the criterion variable [7]. The equation relating criterion variable to one or more predictor variables is called the prediction equation.
Una herramienta fundamental de análisis regional es la ecuación que relaciona dos o más variables hidrológicas. La variable para la que se dan los valores se llama variable predictor. La variable para la que se deben estimar los valores se llama variable criterio [7]. La ecuación que relaciona la variable criterio a una o más variables predictoras se llama la ecuación de predicción.
The objective of regression analysis is to evaluate the parameters of the prediction equation relating the criterion variable to one or more predictor variables. The predictor variables are those whose variation is believed to cause or agree with variation in the criterion variable.
El objetivo del análisis de regresión es evaluar los parámetros de la ecuación de predicción que relaciona la variable criterio a una o más variables predictoras. Las variables predictoras son aquellas cuya variación se cree que causa o acuerde con la variación en la variable criterio.
Correlation provides a measure of the goodness of fit of the regression. Therefore, while regression provides the parameters of the prediction equation, correlation describes its quality. The distinction between correlation and regression is necessary because the predictor and criterion variables cannot be switched unless the correlation coefficient is equal to 1. Stated in other terms, if a criterion variable Y is regressed on a predictor variable X, the regression parameters cannot be used to express X as a function of Y, unless the correlation coefficient is 1. In hydrologic modeling, regression analysis is useful in model calibration; correlation is useful in model formulation and verification.
La correlación proporciona una medida de la bondad del ajuste de la regresión. Por lo tanto, mientras que la regresión proporciona los parámetros de la ecuación de predicción, la correlación describe su calidad. La distinción entre correlación y regresión es necesario porque las variables predictoras y criterio no se puede cambiar a menos que el coeficiente de correlación es igual a 1. Expresado en otros términos, si una variable criterio Y es retrocedido en una variable predictor X, los parámetros de regresión no pueden ser usados para expresar X como una función de Y, a menos que el coeficiente de correlación es 1. En el modelo hidrológico, el análisis de regresión es útil en la calibración del modelo; la correlación es útil en la formulación y verificación del modelo.
The principle of least squares is used in regression analysis as a means of obtaining the best estimates of the parameters of the prediction equation. The principle is based on the minimization of the sum of the squares of the differences between observed and predicted values. The procedure can be used to regress one criterion variable on one or more predictor variables.
El principio de los mínimos cuadrados se utiliza en el análisis de regresión como un medio de obtener las mejores estimaciones de los parámetros de la ecuación de predicción. El principio se basa en la minimización de la suma de los cuadrados de las diferencias entre los valores observados y los predichos. El procedimiento se puede utilizar para la regresión de una variable criterio a una o más variables predictoras. *************
One-Predictor-Variable Regression
Regresión de una Variable Predictora
Assume a predictor variable x, a criterion variable y, and a set on n paired observations of x and y. In the simplest linear case, the line to be fitted has the following form:
Asumir una variable predictora x, una variable criterio de y, y un conjunto de n observaciones pareadas de x y y. En el caso lineal más simple, la línea que se va equipada tiene la siguiente forma:
| y' = α + βx | (7-24) |
in which y' is an estimate of y, and α and β are parameters to be determined by regression.
en el que y' es una estimación de y, y α y β son parámetros que se determinan por la regresión.
In the least squares procedure, values of the intercept α and slope β are sought such that y' is the best estimate of y. For this purpose, the sum of the squares of the differences between y and y' are minimized as follows:
En el procedimiento de mínimos cuadrados, los valores de la intercepción α y la pendiente β se buscan tal que y' es la mejor estimación de y. Para este propósito, la suma de los cuadrados de las diferencias entre y y y' se minimizan como sigue:
| Σ ( y - y' )2 = Σ [ y - ( α + βx ) ] 2 | (7-25) |
in which the symbol Σ indicates the sum of all values from i = 1 to i = n.
en la que el símbolo Σ indica la suma de todos los valores de i = 1 hasta i = n.
Setting the partial derivatives equal to zero:
Ajustando las derivadas parciales iguales a cero:
|
∂ ____ { Σ [ y - ( α + βx ) ] 2 } = 0 ∂α | (7-26) |
|
∂ ____ { Σ [ y - ( α + βx ) ] 2 } = 0 ∂β | (7-27) |
This leads to the normal equations:
Esto lleva a las ecuaciones normales:
| Σ y - nα - β Σ x = 0 | (7-28) |
| Σ xy - α Σ x - β Σ x2 = 0 | (7-29) |
Solving Eqs. 7-28 and 7-29 simultaneously gives:
Resolviendo las ecuaciones 7-28 y 7-29 simultáneamente da:
|
Σ xy - ( Σ x Σ y ) / n β = ________________________ Σ x2 - ( Σ x )2 / n | (7-30) |
|
Σ y
- β Σ x α = __________________ n | (7-31) |
Since the slope of the regression line is: β = ρ σy /σx, the estimate from sample data is:
Dado que la pendiente de la línea de regresión es: β = ρ σy /σx, la estimación de los datos de la muestra es:
|
sx r = β ____ sy | (7-32) |
The standard error of estimate of the correlation is the square root of the variance of the conditional distribution:
El error estándar de estimación de la correlación es la raíz cuadrada de la varianza de la distribución condicional:
|
1 se = [ ______ Σ (y - y' )2 ] 1/2 n - 2 | (7-33) |
in which n - 2 is the number of degrees of freedom, i.e., the sample size minus the number of unknowns.
en el que n - 2 es el número de grados de libertad, es decir, el tamaño de la muestra menos el número de incógnitas.
Alternatively, the standard error of estimate can be estimated from the variance of the conditional distribution, Eq. 7-23. For calculations based on sample data, the standard error of estimate is:
Alternativamente, el error típico de estimación puede estimarse a partir de la varianza de la distribución condicional, Eq. 7-23. Para los cálculos basados en datos de la muestra, el error estándar de estimación es:
|
n - 1 se = sy [ ______ (1 - r 2) ] 1/2 n - 2 | (7-34) |
Nonlinear Equations.
Equations 7-30 and 7-31 can also be used to fit power functions of the type
Las ecuaciones no lineales.
Las ecuaciones 7-30 y 7-31 también se pueden utilizar para adaptarse a funciones de potencia del tipo
Example 7-2.
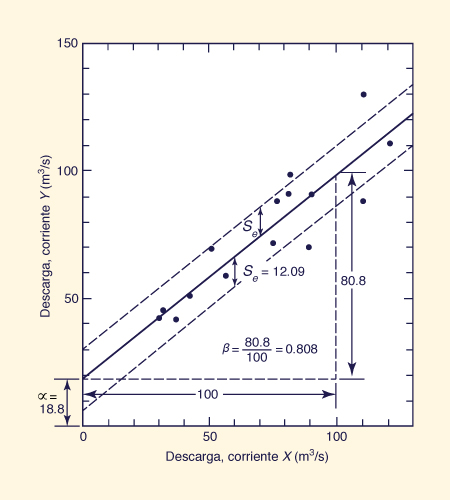
Find the regression equation linking the low flows (annual minima series) of streams X and Y shown in Cols. 2 and 3 of Table 7-1. Calculate the linear regression parameters α and β, the correlation coefficient, and the standard error of estimate.
Encuentre la ecuación de regresión que une los flujos bajos (series mínimos anuales) de los arroyos de X y Y mostrado en Cols. 2 y 3 de la Tabla 7-1. Calcular
los parámetros de regresión lineal α y β, el coeficiente de correlación, y el error estándar de la estimación.
Summing up the values of Cols. 2 and 3, and dividing by n = 15, the means are obtained: x̄ = 72 m3/s and ȳ = 77 m3/s.
Resumiendo los valores de las Columnas 2 y 3, y dividiendo por n = 15, se obtienen los medios:
x̄ = 72 m3/s y ȳ = 77 m3/s.
Columns 4 and 5 show the square of the deviations from the means. Summing up Cols. 4 and 5, dividing the sums by (n - 1) = 14, and taking the square roots, the standard deviations sx = 29.568 m3/s and sy = 26.589 m3/s are obtained.
Las columnas 4 y 5 muestran el cuadrado de las desviaciones de los medios. Resumiendo las
columnas 4 y 5, dividiendo la suma por (n - 1) = 14, y tomando las raíces cuadradas,
las desviaciones estándar sx = 29.568 m3/s y s y = 26.589 m3/s son obtenidas.
Column 6 shows the x2 values, and Col. 7, the xy values.
The sum of these values is: Σ x2 = 90,000 and Σ xy = 93,056.
La Columna 6 muestra los valores x2 y la Col. 7, los valores xy.
La suma de estos valores es: Σ x2 = 90,000 y Σ xy = 93,056.
Using Eq. 7-30: β = [93,056 - (1,080 × 1,155)/ 15 ] / [ 90,000 - (1,080 × 1,080)/ 15] = 0.80849.
Usando la Ec. 7-30: β = [93,056 - (1,080 × 1,155)/ 15 ] / [ 90,000 - (1,080 × 1,080)/ 15] = 0.80849.
Using Eq. 7-31: α = [1155 - (0.8085 × 1080)] / 15 = 18.7882.
Usando la Ec. 7-31: α = [1155 - (0.8085 × 1080)] / 15 = 18.7882.
Using Eq. 7-32, the correlation coefficient is: r = 0.80849 × 29.568 / 26.589 = 0.899.
Usando la Ec. 7-32, el coeficiente de
correlación es: r = 0.80849 × 29.568 / 26.589 = 0.899.
Using Eq. 7-34, the standard error of estimate is: se = 26.589 × [(14/13) (1 - 0.8992)] 1/2 = Usando la Ec. 7-34, el error estándar
de estimación es: se = 26.589 × [(14/13) (1 - 0.8992)] 1/2 =
The data and regression line are plotted in Fig. 7-3.
Los datos y la línea de regresión se representan en la Fig. 7-3.
ONLINE CALCULATION. Using
ONLINEREGRESSION11,
the answer
is: α = 18.7882;
CALCULO EN LÍNEA. Usando
ONLINEREGRESSION11,
la respuesta
es: α = 18,7882;
Figure 7-3
Regresión (una variable predictora): Ejemplo 7-2.
Multiple Regression
Regresión múltiple
The extension of the least squares technique to more than one predictor variable is referred to as multiple regression.
In the case of two predictor variables, x1 and x2, with criterion variable y and a set of n observations of y, x1 and x2, the line to be fitted is:
La extensión de la técnica de mínimos cuadrados para más de una
variable predictor se conoce como regresión múltiple.
En el caso de dos variables predictoras, x1 y x2, con
la variable criterio y y un conjunto de n observaciones de y, x1 y x2, la línea a ser ajustada es:
in which x1 and x2 are measured values and y' is an estimate of y.
en el que x1 y x2 se miden los valores y y' es una estimación de y.
As with the two variable case, values of the intercept α and slopes β1 and β2 are sought such that y' is the best estimate of y.
For this purpose, the sum of the squares of the differences between y and y' are minimized.
Al igual que con el caso de dos variables, los valores de la intercepción α y las pendientes β1 y β 2 se buscan tal que y' es la mejor estimación de
y. Para este propósito, la suma de los cuadrados de las diferencias entre y e y' se minimizan.
Setting the partial derivatives with respect to α, β1 and β2 equal to zero leads to the normal equations:
Colocando las derivadas parciales con respecto a α, β 1 y β2 igual a cero
conduce a las ecuaciones normales:
Solving Eqs. 7-37 to 7-39 simultaneously:
Resolviendo las ecuaciones 7-37 a 7-39 simultáneamente:
As in the case of the one-predictor-variable regression, the standard error of estimate of the correlation is the square root of the variance of the conditional distribution:
Como en el caso de la regresión de un predictor-variable, el error estándar de
estimación de la correlación es la raíz cuadrada de la varianza de la
distribución condicional:
in which n - 3 is the number of degrees of freedom.
en el que n - 3 es el número de grados de libertad.
Alternatively, the standard error of estimate can be estimated from the variance of the conditional distribution. For calculations based on sample data, the standard error of estimate is:
Alternativamente, el error estándar de estimación puede estimarse a partir de la varianza de
la distribución condicional. Para los cálculos basados en datos de la muestra, el error
estándar de estimación es:
in which R = multiple regression coefficient, or coefficient of multiple determination, calculated as follows [8]:
en el que R = coeficiente de regresión múltiple, o coeficiente de
determinación múltiple, calculado de la siguiente manera [8]:
in which SSE = error sum of squares, defined as
en el que SSE = suma de cuadrados, definido como
and SSTO = total sum of squares, defined as
y SSTO = suma total de cuadrados, definido como
Nonlinear Multiple Regression
Regresión múltiple no lineal
Equations 7-40 to 7-42 can also be used to fit equations of the type:
Las ecuaciones 7-40 a 7-42 también se puede utilizar para adaptarse a ecuaciones del tipo:
First, this equation is linearized by taking the logarithms:
En primer lugar, esta ecuación se linealiza mediante la adopción de los logaritmos:
With u = log x1 v = log x2, and w = log y, this equation is: w = log a + bu + cv.
The variables u, v, and w are used in Eqs. 7-40 to 7-42 instead of x1, x2, and y, respectively.
Then α = log a, β1 = b1, β2 = b2, and the regression equation is:
Con u = log x1 v = logx2 y w = logy,
esta ecuación es: w = loga + bu + cv.
Las variables u, v y w se utilizan en las ecuaciones 7-40 a 7-42 en lugar de x1, x2 y y, respectivamente.
Entonces α = log a, β1 = b1, β2 = b2, y la ecuación de regresión es:
Multiple regression analysis involving more than two predictor variables is based on the same least squares principle as in the cases shown here.
Library programs are usually available to perform the large amount of computations involved.
El análisis de regresión múltiple que participaron más de dos variables predictoras
se basa en el mismo principio de mínimos cuadrados como en los casos que se muestran aquí.
Los programas de la biblioteca están generalmente disponibles para llevar a cabo la gran cantidad de
cálculos involucrados.
7.3 ANÁLISIS REGIONAL
Peak Flow Based on Catchment Area
Pico de Flujo Basado en Área de Captación
The earliest approach to regionalization of hydrologic properties was to assume that peak flow is related to catchment area and to perform a regression to determine the parameters.
The equation is of the following form:
La primera aproximación a la regionalización de las propiedades hidrológicas
era suponer que el flujo máximo está relacionado con el área de captación y para realizar una regresión para determinar los parámetros.
La ecuación es de la siguiente forma:
in which Qp = peak flow; A = catchment area; and c and m are regression parameters.
In nature, as catchment area increases, the spatially averaged rainfall intensity decreases, and consequently peak flow does not increase as fast as catchment area.
Therefore, the exponent m in Eq. 7-51 always less than 1, usually in the range 0.4 to 0.9 [5, 10] .
Practical examples of the use of this method are given in Section 14.6.
en el que Qp = flujo máximo; A = área de captación; y c y m son parámetros de regresión.
En la naturaleza, a medida que aumenta el área de captación, la intensidad de la precipitación
promediada espacialmente disminuye, y consecuentemente el flujo máximo no aumenta tan rápido como
el área de captación.
Por lo tanto, el exponente m en la Ec. 7-51 siempre menor que 1, por lo general en el rango de 0.4
a 0.9 [5, 10].
Los ejemplos prácticos del uso de este método se dan en la Secció;n 14.6.
Other formulas relating peak flow to catchment area are the following:
Otras fórmulas relativas de flujo máximo para el área de captación son las siguientes:
in which a, b, c, d, m, and n are parameters determined from statistical analysis of measured data and are applicable on a regional basis, i.e., for neighboring watersheds of similar physiographic, vegetative, and land use patterns.
en el que a, b, c, d, m y n son parámetros determinados a partir de un
análisis estadístico de los datos medidos y son aplicables a nivel regional, es decir, para las cuencas hidrográficas vecinas de la fisiográfica similars, vegetativa, y los patrones de uso de la tierra.
The Creager curves (Fig. 2-73) are an example of Eq. 7-52 [3]. Equation 7-53 been used in regional flood studies in the Southwest [2, 6, 9], whereas Eq. 7-54 appears to be typical of European practice [5].
In principle, none of these equations accounts explicitly for flood frequency, being limited to providing a maximum flow.
The effect of flood frequency, however, can be accounted for by varying the parameters (Section 14.6).
Las curvas Creager (Fig. 2-73) son un ejemplo de la Ec. 7-52 [3]. La Ec. 7-53 ha sido utilizado en estudios de inundaciones regionales en el Suroeste [2, 6, 9], mientras que la Ec. 7-54 parece ser típico de
la práctica Europea [5].
En principio, ninguna de estas ecuaciones representa explícitamente para la frecuencia de
inundación, estar limitado a proporcionar un flujo máximo.
El efecto de la frecuencia de inundaciones, sin embargo, puede ser explicada por la
variación de los parámetros (Sección 14.6).
Index-Flood Method / Método Índice-Inundación
The index-flood method is used to determine the magnitude and frequency of peak flows for catchments of any size, whether gaged or ungaged, located within a hydrologically homogeneous region, i.e. , a region with similar hydrologic characteristics [1, 4].
El método índice-inundación se utiliza para determinar la magnitud y
la frecuencia de los caudales máximos para las cuencas de cualquier tamaño,
ya sea amordazada o no aforadas, situada dentro de una región hidrológicamente
homogénea, es decir, una región con características hidrológicas similares [1, 4].
The application of the index-flood method consists of developing two curves.
The first curve depicts the mean annual flood (i.e., that corresponding to the 2.33-y frequency) versus catchment area.
The second curve shows peak flow ratio versus frequency.
The peak flow ratio is the ratio of peak flow for a given frequency to the mean annual flood.
Using these two curves, a flood-frequency curve may be developed for any catchment in the region.
La aplicación del método índice de inundación consiste en desarrollar dos curvas.
La primera curva representa la inundación anual media (es decir, el correspondiente a la
frecuencia de 2.33-y) frente el área de captación.
La segunda curva muestra la relación de flujo pico frente a la frecuencia.
La relación de flujo máximo es la relación de flujo máximo
para una frecuencia dada a la inundación media anual.
El uso de estas dos curvas, una curva de inundación-frecuencia puede ser desarrollado para cualquier
captación en la región.
The procedure consists of the following steps:
El procedimiento consta de los siguientes pasos:
La medición del área de captación,
El uso de la primera curva para obtener la inundación media anual,
El uso de la segunda curva para obtener las relaciones de flujo máximo para las
frecuencias seleccionadas,
Cálculo de los flujos máximos para cada frecuencia, y
Gráficos de los flujos pico frente las frecuencias.
Mean Annual Flood
El Flujo Medio Anual
The magnitude of the mean annual flood is a function of several physiographic and meteorologic factors.
The physiographic factors that may influence the mean annual flood are the following:
La magnitud del flujo medio anual es una función de varios factores fisiográficos
y meteorológicos. Los factores fisiográficos que pueden influir en la inundación
anual media son los siguientes:
Área de drenaje,
Almacenamiento de canal,
Almacenamiento artificial o natural en lagos y estanques,
Pendiente de captación,
Pendiente del terreno,
La densidad de corriente y el patrón,
Elevación media,
La forma de captación,
Posición orográfica,
Geología subyacente,
Cobertura del suelo, y
Vegetativas y los patrones de uso de la tierra.
The meteorologic factors include:
Los factores meteorológicos incluyen:
Características climáticas regionales,
Intensidades de lluvia,
Dirección de la tormenta, el patrón y el volumen,
Efecto de la nieve derretida.
Of the above factors, drainage area is the most important and the one most readily available.
Measuring the other factors is usually more difficult.
For instance, channel storage has an important effect but cannot be measured directly.
For practical use, a regression of mean annual flood on catchment area is usually sufficient.
Alternatively, equations relating mean annual flood to catchment characteristics other than area can be determined by using multiple regression techniques.
De los factores mencionados, área de drenaje es la más importante y la más
fácil de conseguir.
La medición de los otros factores suele ser más difícil.
Por ejemplo, el almacenamiento del canal tiene un efecto importante pero no se puede medir directamente.
Para el uso práctico, una regresión de la inundación media anual en el área
de inundación suele ser suficiente. Alternativamente, las ecuaciones que relacionan la inundación media anual a las características de captación sean de superficie se pueden determinar
mediante el uso de técnicas de regresión múltiple.
Regional Frequency Curve.
Curva Regional de frecuencia.
The procedure to develop a regional frequency curve by the index-flood method consists of the following steps:
El procedimiento para desarrollar una curva de frecuencia regional mediante el método del
índice de las inundaciones se compone de los siguientes pasos:
Assemble the records (annual exceedence or annual maxima series) of several stations (usually 10 to 15), each having more than 5 y of record.
Montar los registros (excedencia anual o series máximos anuales) de varias estaciones
(por lo general de 10 a 15), cada uno con más de 5 años de registro.
Select a time base common to all the stations (common base period of analysis) in order to eliminate the effect of variability with time.
Seleccionar una base de tiempo común a todas las estaciones (período de
base común de análisis) con el fin de eliminar el efecto de la variabilidad con el tiempo.
For each i th station, rank the records in descending order and compute return periods using a plotting position formula such as Weibull's (Eq. 6-26).
Para cada i th estación, clasifica los registros en orden descendente y calcular
los períodos de retorno utilizando una fórmula de posición gráfica como la de Weibull (Ec. 6.26).
For each i th station, plot the annual flows versus return periods on extreme value probability paper and fit a line visually to determine the frequency curve.
Para cada i th estación, graficar los flujos anuales frente a periodos de retorno
en el papel de probabilidad de valores extremos y ajustar una línea visual para
determinar la curva de frecuencia.
For each i th station, determine the mean annual flood, that is, the peak flow corresponding to the 2.33-y frequency.
Para cada i th estación, determinar la inundación media anual, es decir,
el flujo pico correspondiente a la frecuencia de 2.33-y.
Choose several frequencies, and for each i th station and j th frequency calculate the peak flow ratio, i.e., the ratio of peak flow for the j th frequency to the mean annual flood.
Elija varias frecuencias, y para cada i th estación y j th frecuencia calcular
la relación de flujo máximo, es decir, la relación de flujo máximo para la j th frecuencia a la inundación media anual.
For each j th frequency, determine the median value of peak flow ratios for all stations, that is, the median peak flow ratio.
Para cada j th frecuencia, determinar el valor de la mediana de los relaciones de flujo máximo
para todas las estaciones, es decir, la relación de flujo máximo mediana.
Plot median peak flow ratios versus frequencies on extreme value probability paper and draw a line of best fit to obtain a regional flood frequency curve for the given data.
Gtraficar la relación de la mediana del flujo máximo frente a frecuencias en el papel de probabilidad de valores extremos y graficar una línea que mejor ajuste para obtener una curva de frecuencia de inundación regional de los datos correspondientes.
Test of Hydrologic Homogeneity. / Prueba de Homogeneidad Hidrológica.
The index-flood method includes a test of regional hydrologic homogeneity. Any station not passing this test should be excluded from the set. The test procedure consists of the following steps [4]:
El método del índice de inundaciones incluye una prueba de homogeneidad hidrológica regional.
Cualquier estación que no pase esta prueba debe ser excluido del conjunto. El procedimiento de ensayo
consta de los pasos siguientes [4]:
For each i th station, use its frequency curve to determine the 2.33-y and the 10-y floods.
Para cada i th estación, utilizar su curva de frecuencia para determinar las inundaciones
2.33-y y 10-y.
For each i th station, calculate the 10-y peak flow ratio, i.e., the ratio of the 10-y flood to the 2.33-y flood.
Para cada i th estación, calcular la relación de flujo máximo de 10-y, es decir,
la relación de la inundación de 10-y a la inundación de 2.33-y.
Calculate the average of the 10-y peak flow ratios for all stations.
Calcular el promedio de las proporciones de flujo máximo de 10-y para todas las estaciones.
For each i th station, multiply the 2.33-y flood by the average 10-y peak flow ratio to obtain an adjusted 10-y peak flow.
Para cada i th estación, multiplique la inundación 2.33-y por
el promedio de la relación de flujo máximo de 10-y para obtener un flujo máximo de 10-y ajustado.
For each i th station, use its frequency curve to determine the return period Ti for the adjusted 10-y peak flow.
Para cada i th estación, utilice su curva de frecuencia para determinar el período de retorno
de Ti para el flujo máximo de 10-y ajustado.
For each i th station, plot the return period Ti versus the length of record n, in years, in Fig. 7-4.
Points located within the confidence limits (solid lines) are considered to be hydrologically homogeneous.
Points lying outside of the solid lines should not be used in the calculation of the median peak flow ratio (step 7 of the index-flood method).
Para cada i th estación, graficar el período de retorno Ti frente
a la longitud de registro n, en los años, en la Fig. 7-4.
Los puntos situados dentro de los límites de confianza (líneas continuas) se consideran que son
hidrológicamente homogéneos.
Los puntos que se encuentran fuera de las líneas sólidas no deben utilizarse en el cálculo de la relación de flujo pico mediano (paso 7 del método del índice de inundaciones).
Figure 7-4 Homogeneity test chart for index-flood method [4].
Limitations of the Index-Flood Method.
Limitaciones del Método Índice-Inundación.
Benson [1] has noted the following limitations of the index-flood method:
Benson [1] ha tomado nota de las siguientes limitaciones del método índice-inundación:
The mean annual flood for stations with short periods of record may not be typical, which means that the peak flow ratios of different return periods may vary widely among stations.
La inundación media anual para estaciones con períodos cortos de registro
no pueden ser típicos, lo que significa que las relaciones de flujo máximo de los diferentes periodos de retorno pueden variar ampliamente entre las estaciones.
The homogeneity test is used to determine whether the differences in the frequency curves are greater than those that could be attributed to chance alone. The index-flood test uses the 10-y flow ratio because of the lack of sufficient data to define the frequency curve adequately at longer return periods.
Studies have shown that although homogeneity may be assumed on the basis of the 10-y peak flow ratio,
the individual frequency curves may show wide and sometimes systematic differences at longer return periods.
La prueba de homogeneidad se utiliza para determinar si las diferencias en las curvas de frecuencia
son mayores que los que podría atribuirse a la casualidad.
La prueba de índice-inundación utiliza la relación de flujo de 10-y debido a la falta de datos suficientes para definir la curva de frecuencia adecuada a largo de períodos de retorno.
Los estudios han demostrado que a pesar de la homogeneidad puede suponerse sobre la base de la
relación de flujo máximo de 10-y, las curvas de frecuencia individuales pueden mostrar
amplias y a veces diferencias sistemáticas en períodos de retorno más largos.
The method combines frequency curves for all catchment sizes, excluding only the largest.
At the 10-y peak flow ratio level, the effect of catchment size is small and can be neglected. Studies have shown that the peak flow ratios tend to vary inversely with catchment size. In general, the larger the catchment,
the flatter the frequency curve and the lower the peak flow ratios. The effect of catchment size is particularly marked for floods of long return period.
El método combina curvas de frecuencia para todos los tamaños de captación,
excluyendo sólo el más grande.
A nivel de relación de flujo máximo de 10-y, el efecto del tamaño de captación
es pequeña y se puede despreciar. Los estudios han demostrado que las relaciones de flujo máximo
tienden a variar inversamente con el tamaño de captación. En general, cuanto mayor sea
la captación, más plana la curva de frecuencia y las relaciones de flujo máximo inferior.
El efecto del tamaño de captación es particularmente marcado por las inundaciones de
periodo de retorno de largo.
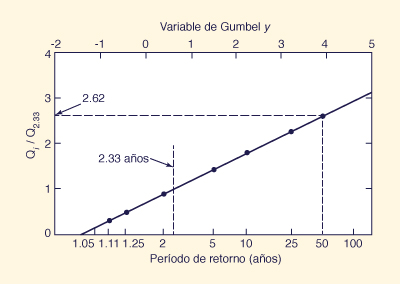
Example 7-3.
Use the Qi/Q2.33 data for the five stations shown in Table 7-2 to develop a regional flood frequency curve by the index-flood method.
Assuming Q2.33 = 2.5A0.6, in which Q2.33 is in cubic meters per second and catchment area A is in square kilometers, calculate the 50-y flood for a 150-km2 catchment based on the regionally developed curve.
Utilice los datos Qi/Q2.33 para las cinco estaciones que se muestran en la
Tabla 7-2 para desarrollar una curva de frecuencia de inundación regional mediante el método
del índice de las inundaciones.
Suponiendo Q2.33 = 2.5A0.6 , en el que Q2.33
está en metros cúbicos por segundo y el área de captación A
está en kilómetros cuadrados, calcular la inundación para 50-y de una cuenca de 150-km2 basada en la curva desarrollada regionalmente.
The median values are shown at the bottom of each column.
These values are plotted against the return period, as shown in Fig. 7-5.
The fitted line is the regional flood-frequency curve.
For a 150-km2 catchment, the mean annual flood is: 50.5 m3/s.
From Fig. 7-5, the peak flood ratio for the 50-y return period is 2.62.
Therefore, the 50-y flood for this catchment is 132 m3/s.
Los valores de la mediana se muestran en la parte inferior de cada columna.
Estos valores se grafican frente el período de retorno, como se muestra en la Fig. 7-5.
La línea ajustada es la curva de frecuencia de inundación regional.
Para una cuenca de 150-km2, la inundación media anual es de: 50.5 m3/s.
De la Fig. 7-5, la relación de flujo máximo para el periodo de retorno de 50-y es de 2.62.
Por lo tanto, la inundación de 50-y para esta cuenca es de 132 m3/s.
Figure 7-5 Index-flood method: Example 7-3. / Método Índice-Inundación: Ejemplo 7-3.
Las precipitaciones de Intensidad-Duración-Frecuencia
Curves showing the relationship between intensity, duration, and frequency of rainfall (IDF curves) are required for peak flow computations in small catchments (see rational method, Chapter 4).
These curves can be developed using either: (a) depth-duration-frequency data provided by the National Weather Service, or (b) regional or local rainfall intensity-duration data.
The latter procedure is illustrated by the following example.
Se requieren curvas que muestran la relación entre la intensidad, duración y frecuencia
de las precipitaciones (curvas IDF) para cálculos de flujo máximo requeridas
en pequeñas cuencas (véase el método racional, capítulo 4).
Estas curvas se pueden desarrollar utilizando ya sea: (a) los datos de profundidad-duración-frecuencia proporcionados por el Servicio Meteorológico Nacional, o (b) datos de precipitaciones regionales o locales de intensidad-duración. Este último procedimiento se ilustra mediante el siguiente ejemplo.
Example 7-4.
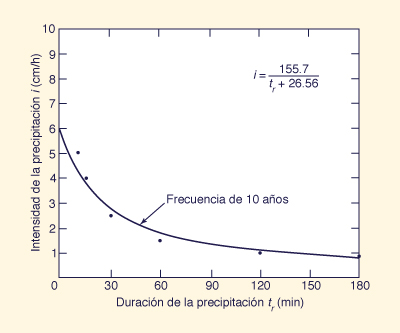
Determine the equation relating rainfall intensity and duration for the following 10-y frequency rainfall data.
Determinar la ecuación que relaciona la intensidad de precipitación y la duración
de los siguientes datos de precipitación de 10-y de frecuencia.
The data suggest that the relation is of hyperbolic type, with greater intensities associated with shorter durations.
Therefore, an equation of the type of Eq. 2-6 is applicable:
Los datos sugieren que la relación es de tipo hiperbólico, con mayor intensidad
asociado con duraciones más cortas. Por lo tanto, una ecuación del tipo de la Ec. 2-6 es aplicable:
in which a and b are constants to be determined by regression analysis.
This equation can be linearized in the following way:
en la que a and b son constantes a determinar por el análisis de regresión.
Esta ecuación se puede linealizar de la siguiente forma:
With y = 1/i, x = tr, α = b/a, and β = 1/a, the application of the regression formulas (Eqs. 7-30 and 7-31) to the data leads to: 1/i = 0.006422 tr, + 0.1706, in which α = 0.1706 and β = 0.006422.
Therefore: a = 155.7 and b = 26.56.
The regression equation is: i = 155.7 / (tr + 26.56).
The data and regression line are shown in Fig. 7-6.
Con y = 1/i, x = tr, α = b/a, y β = 1/a,
la aplicación de las fórmulas de regresión (Ecs. 7-30 y 7-31)
a los datos conduce a 1/i = 0.006422 tr, + 0.1706, en el que α = 0.1706 y β = 0.006422.
Por lo tanto: a = 155.7 y b = 26.56.
La ecuación de regresión es: i = 155.7 / (tr + 26.56).
Los datos y la línea de regresión se muestran en la Fig. 7-6.
ONLINE CALCULATION. Using
ONLINEREGRESSION15,
the answer
is: a = 155.702;
CALCULADORA EN LÍNEA. Usando
ONLINEREGRESSION15, la respuesta es: a = 155.702;
Figure 7-6 Ajuste de curvas de intensidad-duración-frecuencia: Ejemplo 7-4.
Ecuaciones de Estado para la Frecuencia de Inundación Regional
The U.S. Geological Survey has developed a comprehensive methodology for regional analysis of flood frequency [11].
Details of this method are given in Section 14.6.
El Servicio Geológico de Estados Unidos ha desarrollado una metodología completa para el
análisis regional de la frecuencia de inundaciones [11]. Los detalles de este método se dan
en la Sección 14.6.
PREGUNTAS
What is a joint probability? What is a marginal probability?
¿Qué es una probabilidad conjunta? ¿Qué es una probabilidad marginal?
What is a joint density function? Give an example.
¿Qué es una función de densidad conjunta? Dar un ejemplo.
What is a conditional probability? How is it used in regression analysis?
¿Qué es una probabilidad condicional? ¿Cómo se utiliza en el análisis de regresión?
Define covariance.
Definir la covarianza.
What is a correlation coefficient?
¿Qué es un coeficiente de correlación?
What is the difference between correlation and regression?
¿Cuál es la diferencia entre correlación y regresión?
Describe briefly the index-flood method for regional analysis of flood frequency.
Describir brevemente el método de índice-inundación para el análisis
regional de la frecuencia de inundaciones.
PROBLEMAS
Using ONLINE TWOD CORRELATION,
calculate the correlation coefficient of the following joint distribution of quarterly flows (expressed as mean values in each class) in streams A and B:
Usando ONLINE TWOD CORRELATION, calcular el coeficiente de
correlación de la siguiente distribución conjunta de los flujos trimestrales (expresado como valores medios en cada clase) en las
corrientes A y B:
Develop a spreadsheet to calculate the regression constants, correlation coefficient, and standard error of estimate of a series of paired flow values X and Y. Test your program using the data of Example 7-2 in the text.
Desarrollar una hoja de cálculo para calcular las constantes de regresión,
el coeficiente de correlación, y el error estándar de la estimación
de una serie de valores de flujo pareadas X e Y.
Probar su programa usando los datos del ejemplo 7-2 en el texto.
Using the spreadsheet developed in Problem 7-2, calculate the regression constants, correlation coefficient, and standard error of estimate for the following paired low-flow series (annual minima):
El uso de la hoja de cálculo desarrollado en el Problema 7-2, calcular las constantes de regresión,
el coeficiente de correlación y el error estándar de estimación para la siguiente serie de bajo flujo pareadas (mínimos anuales):
Verify with ONLINE REGRESSION11.
Verifique con ONLINE REGRESSION11.
Modify the spreadsheet developed in Problem 7-2 to calculate the regression constants to fit a power function of the following form (Eq. 7-51):
in which Qp = peak discharge; A = drainage area; c and m are coefficient and exponent, respectively.
Using the spreadsheet, fit a power function to the following data:
Modificar la hoja de cálculo desarrollada en el Problema 7-2 para el cálculo de las constantes
de regresión para adaptarse a una función de potencia de la siguiente forma (Ec. 7-51):
en el que Qp = descarga máxima; A = área de drenaje;
c y m son coeficiente y exponente, respectivamente.
Uso de la hoja de cálculo, se ajusta a una función de potencia a los siguientes datos:
Verify with ONLINE REGRESSION12.
Verifique con ONLINE REGRESSION12.
ONLINE REGRESSION13 solves the two-predictor-variable
linear regression problem
La calculadora ONLINE REGRESSION13 resuelve el problema de regresión lineal de dos variables-predictoras
Use ONLINE REGRESSION14
to solve the two-predictor-variable nonlinear regression problem of Eq. 7-48, for the data of Problem 7-5.
Utilizar ONLINE REGRESSION14 para resolver el problema de
regresión no lineal de dos variables predictoras de la Ec 7-48, para los datos de Problema 7-5.
The median Qi/Q2.33 ratios (i = frequency) for 10 stations have been found to be 1.95 for the 10-y frequency and 2.45 for the 50-y frequency.
Use the index-flood method to calculate the 25-y flood for a point in a stream having a 340-km2 catchment and a mean annual flood given by the following formula:
La mediana de las relaciones Qi / Q2.33(i = frecuencia)
para 10 estaciones se han encontrado para ser 1.95 para la frecuencia de 10-y y 2.45 para la frecuencia
de 50-y. Utilizar el método de índice de inundación para calcular la
inundación de 25-y para un punto en una corriente que tiene una cuenca de 340-km2
y una inundación anual promedio dada por la siguiente fórmula:
in which Q = flood discharge in cubic meters per second, and A = drainage area in square kilometers.
en la que Q = inundación de descarga en metros cúbicos por segundo, y
A = área de drenaje en kilómetros cuadrados.
Modify the spread sheet developed in Problem 7-2 to calculate the regression constants and correlation coefficient to fit intensity-duration-frequency rainfall data. Test your spread sheet using the data of Example 7-4 in the text.
Modificar la hoja de cálculo desarrollada en el Problema 7-2 para calcular las
constantes de regresión y el coeficiente de correlación para ajustar
los datos de precipitación de intensidad-duración-frecuencia.
Probar su hoja de cálculo utilizando los datos del Ejemplo 7-4 en el texto.
Using ONLINE REGRESSION15 for a hyperbolic regression,
calculate the regression constants a and b (Eq. 7-55) for the following 25-y frequency rainfall data:
Usando la calculadora ONLINE REGRESSION15 para una regresión hiperbólica, calcular las constantes de regresión a and b (Ec. 7-55) para los siguientes datos de
precipitación de 25-y de frecuencia:
BIBLIOGRAFÍA
Benson, M. A. (1962). "Evolution of Methods for Evaluating the Occurrence of Floods," U.S. Geological Survey Water Supply Paper No. 1580-A.
Boughton, W. C., and K. G. Renard. (1984). "Flood Frequency Characteristics of Some Arizona Watersheds," Water Resources Bulletin, Vol. 20, No. 5, October, pp. 761- 769.
Creager, W. P., J. D. Justin, and 1. Hinds. (1945). Engineering for Dams. Vol. 1. New York: John Wiley.
Dalrymple, T. (1960). "Flood Frequency Analyses," U.S. Geological Survey Water Supply Paper No. 1543A.
Hall, M. J. (1984). Urban Hydrology. London: Elsevier Applied Science Publishers.
Malvick, A. J. (1980). "A Magnitude-Frequency-Area Relation for Floods in Arizona," Research Report No. 2, College of Engineering, University of Arizona, Tucson.
McCuen, R. H. (1985). Statistical Methods for Engineers. Englewood Cliffs, N.J.: Prentice-Hall.
Neter, J., W. Wasserman, and M. H. Kutner. (1989). Applied Linear Regression Models, Second Edition, Irwin, Homewood, illinois.
Reich. B. M., H. B. Osborn. and M. C. Baker. (1979). "Tests on Arizona New Flood Estimates," in Hydrology and Water Resources in Arizona and the Southwest, University of Arizona, Tucson, Vol. 9.
Roeske, R. H. (1978). "Methods for Estimating the Magn!tude and Frequency of Floods in Arizona," Final Report, ADOT-RS-lS-121, U.S. Geological Survey, Tucson, Arizona.
U.S. Geological Survey. (1994). "Nationwide Summary of U.S. Geological Survey Regional Regression Equations for Estimating Magnitude and Frequency of Floods for Ungaged Sites, 1993" Compiled by M. E. Jennings, W. O. Thomas, and H. C. Riggs, Water-Resources Investigations Report 94-4002, Reston, Virginia.
Viessman, W. Jr., J. W. Knapp, G. L. Lewis, and T. E. Harbaugh, Introduction to Hydrology, 2d. ed, New York: Harper & Row.
Table 7-1 One-Predictor-Variable Regression: Example 7-2.
Tabla 7-1 Regresión de una Variable Predictora: Ejemplo 7-2.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
Year
x
(m3/s)y
(m3/s)( x - x̄ )2
( y - ȳ )2
x2
xy
1973
110
89
1,444
144
12,100
9,790
1974
42
51
900
676
1,764
2,142
1975
75
72
9
25
5,625
5,400
1976
120
112
2,304
1,225
14,400
13,440
1977
89
70
289
49
7,921
6,230
1978
32
45
1,600
1,024
1,024
1,440
1979
37
42
1,225
1,225
1,369
1,554
1980
56
59
256
324
3,136
3,304
1981
82
100
100
529
6,724
8,200
1982
90
92
324
225
8,100
8,280
1983
50
70
484
49
2,500
3,500
1984
30
42
1,764
1,225
900
1,260
1985
81
92
81
225
6,561
7,452
1986
110
130
1,444
2,809
12,100
14,300
1987
76
89
16
144
5,776
6,764
Sum
1,080
1,155
12,240
9,898
90,000
93,056
![]()
![]()
y' = α + β1x1 + β2x2
(7-35)
Σ ( y - y' )2 = Σ [ y - (α + β1x1 + β2x2) ] 2
(7-36)
Σ y - nα - β1 Σx1 - β2 Σx2 = 0
(7-37)
Σ yx1 - αΣ x1 - β1 Σ x12 - β2 Σ x1x2 = 0
(7-38)
Σ yx2 - αΣ x2 - β2 Σ x22 - β1 Σ x1x2 = 0
(7-39)
( nΣyx2 - Σy Σx2 )( nΣx1x2 - Σx1 Σx2 ) - [ nΣx22 - (Σx2 )2] [ nΣyx1 - ΣyΣx1]
β1 = ___________________________________________________________________________________
(nΣx1x2 - Σx1Σx2)2 - [nΣx12 - (Σx1)2] [nΣx22 - (Σx2)2]
(7-40)
( nΣyx1 - Σy Σx1 ) - β1 [nΣx12 - (Σx1)2]
β2 = ______________________________________________
nΣx1x2 - Σx1 Σx2
(7-41)
Σy - β1Σx1 - β2Σx2
α = ___________________________
n
(7-42)
1
se = [ _______ Σ (y - y' )2 ] 1/2
n - 3
(7-43)
n - 1
se = sy [ _______ ( 1 - R 2 ) ] 1/2
n - 3
(7-44)
R 2 = 1 - (SSE / SSTO )
(7-45)
SSE = Σ ( y - y' )2
(7-46)
SSTO = Σ ( y - ȳ )2
(7-47)
y = a x1b1 x2b2
(7-48)
log y = log a + b1 log x1 + b2 log x2
(7-49)
y = 10α x1β1 x2β2
(7-50)
Qp = c A m
(7-51)
Qp = c A nA-m
(7-52)
Qp = c A a - b log A
(7-53)
cA
Qp = ______________ + dA
(a + bA ) m
(7-54)
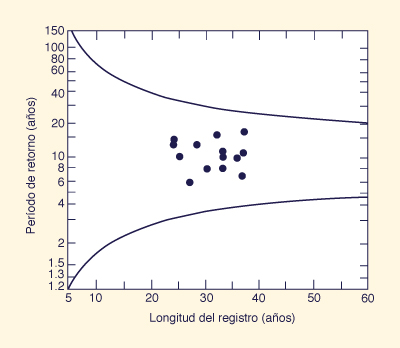
Table 7-2 Index-Flood Method: Example 7-3. / Tabla 7-2 Método de Índice-Inundación: Ejemplo 7-3.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
Station/ Estación
iQi /Q 2.33 for the j th Return Period (years) /Qi /Q 2.33 para la j th Período de Retorno (años)
1.11
1.25
2
5
10
25
50
1
0.32
0.49
0.90
1.45
1.82
2.28
2.62
2
0.35
0.51
0.92
1.44
1.79
2.23
2.56
3
0.39
0.55
0.92
1.40
1.73
2.14
2.44
4
0.27
0.45
0.90
1.50
1.88
2.38
2.74
5
0.31
0.50
0.91
1.46
1.84
2.32
2.68
Median / Mediana
0.32
0.50
0.91
1.45
1.82
2.28
2.62
Rainfall Intensity-Duration-Frequency
Rainfall duration tr (min) / Duración de precipitación tr (min)
5
10
15
30
60
120
180
Rainfall intensity i (cm/h) / Intensidad de precipitación i (cm/h)
8
5
4
2.5
1.5
1.0
0.8
a
i = ___________
tr + b
(7-55)
******************************************************
1 tr b
___ = ____ + ____
i a a
(7-56)
![]()
State Equations for Regional Flood Frequency
Stream A
(ac-ft) /
Arroyo A
(ac-ft) 1000
2000
3000
4000
5000
Stream B
(ac-ft) / Arroyo B
(ac-ft)
1000
0.07
0.03
0.02
0.00
0.00
2000
0.03
0.08
0.04
0.03
0.00
3000
0.02
0.04
0.08
0.05
0.02
4000
0.00
0.04
0.08
0.11
0.06
5000
0.00
0.00
0.03
0.08
0.09
Stream / (Corriente) X
(m3/s)Stream / Corriente Y
(m3/s)50
65
66
76
32
45
78
95
12
18
34
50
23
31
50
64
43
67
89
99
76
89
22
33
Qp = cAn
Qp = cAn
Peak Discharge / Descarga Máxima
(m3/s)Drainage Area / Área de Descarga
(km2)124
25
254
46
378
78
101
22
678
99
540
89
490
83
267
52
350
73
Y
Time of Concentration / Tiempo de Concentración
(min)X1
Hydraulic Length / Longitud Hidráulica
(m)X2
Catchment Slope / Pendiente de Captación
(m/m)89
3245
0.008
75
2567
0.011
57
2783
0.009
34
1234
0.015
101
5345
0.006
121
5329
0.007
68
3002
0.008
79
2976
0.010
25
1034
0.018
59
2984
0.010
96
3892
0.007
12
534
0.020
Q 2.33 = 3.93 A 0.75
Duration / Duración (min)
5
10
15
30
60
120
180
Intensity / Intensidad (mm/h)
15.5
7.5
6.5
4.5
3.5
2.5
1.5
http://engineeringhydrology.sdsu.edu
180914 07:15
