|
|
|
CAPÍTULO 9: TRÁNSITO EN CANALES |
|
"When we started our research at Cornell University in 1964, we intended to show that the St. Venant
equations without simplification were required for the overland flow problem, although we came to quite different conclusions." David A. Woolhiser (1996) |
|
"Cuando empezamos nuestra investigación en la Universidad de Cornell en 1964, teníamos la intención de demostrar que las ecuaciones St. Venant sin simplificación eran requeridas para el problema de flujo superficial, aunque llegamos a conclusiones muy diferentes." David A. Woolhiser (1996) |
|
This chapter is divided into five sections. Section 9.1 describes the Muskingum method, the most widely used method of hydrologic stream channel routing. Sections 9.2 and 9.3 discuss simplified hydraulic routing techniques: kinematic and diffusion waves, respectively. Section 9.4 describes the Muskingum-Cunge method. Section 9.5 introduces the subject of dynamic wave routing, the most complete hydraulic routing technique. Este capítulo se divide en cinco secciones. La Sección 9.1 se describe el método de Muskingum, el método más utilizado para el tránsito del canal de flujo hidrológico. Las Secciones 9.2 y 9.3 discuten técnicas de tránsito hidráulico simplificadas: las ondas cinemáticas y de difusión, respectivamente. La Sección 9.4 se describe el método de Muskingum-Cunge. La Sección 9.5 introduce el tema de tránsito de onda dinámica, la técnica más completa del tránsito hidráulico. |
9.1 EL MÉTODO MUSKINGUM
|
|
Tránsito en Canales
Stream channel routing uses mathematical relations to calculate outflow from a stream channel once inflow, lateral contributions, and channel characteristics are known.
El tránsito del canal de flujo utiliza relaciones matemáticas para calcular la salida de un canal de flujo una vez que se conocen de flujo de entrada, aportes laterales, y las características del canal.
Stream channel routing usually implies open channel flow conditions, although there are exceptions, such as storm sewer flow, for which mixed open channel-closed conduit flow conditions may prevail. In this chapter, stream channel routing refers to unsteady flow calculations in streams and rivers. Channel reach refers to a specific length of stream channel possessing certain translation and storage properties. The hydrograph at the upstream end of the reach is the inflow hydrograph; the hydrograph at the downstream end is the outflow hydrograph. Lateral contributions consist of point tributary inflows and/or distributed inflows; e.g., interflow and groundwater flow.
****1609211600
Tránsito del canal de flujo generalmente implica condiciones de flujo en canal abierto, aunque hay excepciones, como el flujo de drenaje pluvial, para los que mezclan las condiciones de flujo de conducto de canal cerrado abierto pueden prevalecer. En este capítulo, el tránsito del canal de flujo se refiere a los cálculos de flujo inestable en los arroyos y ríos. El tramo del canal se refiere a una longitud específica del canal del arroyo que posee ciertas propiedades de traducción y de almacenamiento. El hidrograma en el extremo de aguas arriba del tramo es el hidrograma de flujo de entrada; el hidrograma en el extremo aguas abajo es el hidrograma de salida. Las contribuciones laterales constan de las entradas de flujo tributarias del punto y/o entradas de flujo distribuidas; por ejemplo, interflujo y el flujo de aguas subterráneas.
The terms stream channel routing and flood routing are often used interchangeably. This is attributed to the fact that most stream channel routing applications are in flood flow analysis, flood control design, or flood forecasting (Fig. 9-1).
Los términos de tránsito del flujo del canal y tránsito de flujo se usan indistintamente. Esto se atribuye al hecho de que la mayoría de las aplicaciones del tránsito de flujo del canal están en el análisis de flujo de inundación, diseño de control de inundaciones, o el pronóstico de inundaciones (Fig. 9-1).
Figure 9-1 Flood stage in a tropical river. / El nivel de inundación en un río tropical. |
Two general approaches to stream channel routing are recognized: (1) hydrologic and (2) hydraulic. As in the case of reservoir routing (Chapter 8), hydrologic stream channel routing is based on the storage concept. Conversely, hydraulic channel routing is based on the principles of mass and momentum conservation. Hydraulic routing techniques are of three types: (1) kinematic wave, (2) diffusion wave, and (3) dynamic wave. The dynamic wave is the most complete model of unsteady open channel flow. Kinematic and diffusion waves are convenient and practical approximations to the dynamic wave.
Se reconocen dos enfoques generales de tránsito de flujo del canal: (1) hidrológico e (2) hidráulico. Al igual que en el caso del tránsito del reservorio (Capítulo 8), el tránsito del canal de flujo hidrológico se basa en el concepto de almacenamiento. A la inversa, el tránsito del canal hidráulico se basa en los principios de conservación de la masa y el momento. Las técnicas del tránsito hidráulico son de tres tipos: (1) onda cinemática, (2) onda de difusión, y (3) onda dinámica. La onda dinámica es el modelo más completo de flujo no permanente en canales abiertos. Las ondas cinemáticas y de difusión son aproximaciones convenientes y prácticas a la onda dinámica.
An alternate approach to hydrologic and hydraulic routing has emerged in recent years. This approach is similar in nature to the hydrologic routing methods yet contains sufficient physical information to compare favorably with the more complex hydraulic routing techniques. This hybrid approach is the basis of the Muskingum-Cunge method of flood routing.
Un enfoque alternativo para el tránsito hidrológico e hidráulico ha surgido en los últimos años. Este enfoque es similar en naturaleza a los métodos de tránsito hidrológico todavía contiene información física suficiente para comparar favorablemente con las más complejas técnicas de tránsito hidráulico. Este enfoque híbrido es la base del método de Muskingum-Cunge del tránsito de inundación.
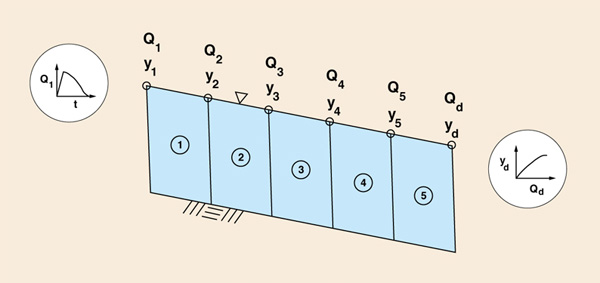
At the outset of the study of stream channel routing, it is necessary to introduce a few basic modeling concepts. A typical hydrologic model consists of: (1) input, (2) system, and (3) output (Fig. 9-2). In surface water hydrology, the system is usually a catchment, a reservoir, or a stream channel. In the case of a catchment, the input is a storm hyetograph. For reservoirs and stream channels, the input is an inflow hydrograph. For all three cases, catchments, reservoirs, and channels, the output is an outflow hydrograph.
Al comienzo del estudio del tránsito del flujo del canal, es necesario introducir algunos conceptos básicos de modelado. Un modelo hidrológico típico consiste en: (1) de entrada, (2) del sistema, y (3) de salida (Fig a 9-2.). En la hidrología de agua superficial, el sistema suele ser una cuenca, un reservorio, o un canal de flujo. En el caso de una cuenca de captación, la entrada es un hyetograma de tormenta. Para reservorios y canales de flujo, la entrada es un hidrograma de entrada de flujo. En los tres casos, las cuencas, reservorios y canales, la salida es un hidrograma de salida de flujo.
Figure 9-2 Entrada, sistema, y salida en un modelo hidrológico típico. |
In general, modeling problems are classified into three types: (1) prediction, (2) calibration, and (3) inversion. In the prediction problem, input and system are known and described by properties or parameters, and the task is to calculate the output based on the knowledge of system and input. For instance, with known inflow hydrograph, lateral contributions, and channel reach parameters, the outflow hydrograph from a stream channel can be computed using routing techniques (Example 9-1).
En general, los problemas de modelado se clasifican en tres tipos: (1) predicción, (2) calibración, e (3) inversión. En el problema de predicción, de entrada y el sistema se conocen y describen por las propiedades o parámetros, y la tarea es calcular la salida basándose en el conocimiento de sistema y de entrada. Por ejemplo, con un hidrograma de flujo de entrada conocido, las contribuciones laterales, y los parámetros del tramo del canal, el hidrograma de salida de flujo de un canal de flujo se puede calcular usando técnicas de tránsito (Ejemplo 9-1).
In the calibration problem, input and output are known, and the objective is to determine the properties or parameters describing the system. In the case of a stream channel, with known upstream inflow, lateral contributions, and outflow hydrograph, the routing parameters are calculated by a calibration procedure (Example 9-2).
En el problema de calibración, la entrada y salida se muestran, y el objetivo es determinar las propiedades o parámetros describiendo el sistema. En el caso del canal de flujo, con flujo de entrada aguas arriba conocido, las contribuciones laterales, el hidrograma de flujo de salida, los parámetros de tránsito son calculados por un prodecimiento de calibración (Ejemplo 9-2).
The inversion problem is the third type of modeling problem. In this case, system and output are known, and the task is to calculate the inflow or inflows. This is accomplished by reversing the routing process in a technique known as inverse channel routing. For instance, with known upstream inflow, outflow, and channel reach parameters, the lateral contributions can be calculated by inverse routing.
El problema de inversión es el tercer tipo de problema de modelado. En este caso, el sistema y la salida son conocidos, y la tarea es calcular el flujo de entrada o entradas. Esto se logra invirtiendo el proceso de tránsito en una técnica conocida como inversa tránsito del canal. Por ejemplo, con flujo de entrada aguas arriba conocida, la salida, y los parámetros del tramo del canal, las contribuciones laterales se pueden calcular por tránsito inverso.
The prediction problem is the more common type of modeling application; however, a calibration is usually required in advance of the prediction. Model verification is the process of testing the model with actual data to establish its predictive accuracy. To calibrate and verify a model, it is usually necessary to assemble two different data sets. The first set is used in model calibration and the second set is used in model verification. A close agreement between calculated and measured data is an indication that the model has been verified. A detailed discussion of these subjects is given in Chapter 13.
El problema de predicción es el tipo más común de la aplicación del modelado; sin embargo, una calibración se requiere generalmente antes de la predicción. La verificación del modelo es el proceso de poner a prueba el modelo con datos reales para establecer su exactitud predictiva. Para calibrar y verificar un modelo, por lo general es necesario montar dos conjuntos de datos diferentes. El primer conjunto se utiliza en la calibración del modelo y el segundo conjunto se utiliza en la verificación del modelo. Un primer acuerdo entre los datos calculados y medidos es una indicación de que el modelo ha sido verificado. Una discusión detallada de estos temas se da en el Capítulo 13.
Muskingum Method/ Método de Muskingum
The Muskingum method of flood routing was developed in the 1930s in connection with the design of flood protection schemes in the Muskingum River Basin, Ohio (Fig. 9-3) [11]. It is the most widely used method of hydrologic stream channel routing, with numerous applications in the United States and throughout the world.
El método de Muskingum de tránsito de inundaciones fue desarrollado en 1930 en relación con el diseño de los planos de protección contra inundaciones en la cuenca del Río Muskingum, Ohio (Fig. 9-3) [11]. Es el método más utilizado para el tránsito del canal de flujo hidrológico, con numerosas aplicaciones en los Estados Unidos y en todo el mundo.
Figure 9-3 The Muskingum river near Marietta, Ohio./ El río Muskingum, cerca de Marietta, Ohio. |
The Muskingum method is based on the differential equation of storage, Eq. 8-4, reproduced here:
El método Muskingum se basa en la ecuación diferencial de almacenamiento, Ec. 8-4, reproducido aquí:
|
dS I - O = _____ dt | (8-4) |
In an ideal channel, storage is a function of inflow and outflow. This is in constrast with an ideal reservoir, in which storage is solely a function of outflow (see Eqs. 8-5 to 8-7). In the Muskingum method, storage is a linear function of inflow and outflow:
En un canal ideal, el almacenamiento es una función del flujo de entrada y flujo de salida. Esto está en constrast con un reservorio ideal, en el que el almacenamiento es únicamente una función del flujo de salida (ver las Ecs. 8-5 8-7). En el método de Muskingum, el almacenamiento es una función lineal de entrada y salida:
| S = K [ X I + ( 1 - X ) O ] | (9-1) |
in which S = storage volume; I = inflow; O = outflow; K = a time constant or storage coefficient; and X = a dimensionless weighting factor. With inflow and outflow in cubic meters per second, and K in hours, storage volume is in (cubic meters per second)-hour. Alternatively, K could be expressed in seconds, in which case storage volume is in cubic meters.
en el que S = volumen de almacenamiento; I = flujo de entrada; O = flujo de salida; K = una constante de tiempo o un coeficiente de almacenamiento; y X = un factor de ponderación adimensional. Con entrada y salida de flujo en metros cúbicos por segundo, y K en horas, el volumen de almacenamiento es de (metros cúbicos por segundo)-hora. Alternativamente, K se podría expresar en segundos, en el caso del volumen de almacenamiento es en metros cúbicos.
Equation 9-1 was developed in 1938 and has been widely used since then [11].
It is esentially a generalization of the linear reservoir concept (Eq. 8-7).
In fact, for X = 0, Eq. 9-1 reduces to Eq. 8-7.
In other words, linear reservoir routing is a special case of Muskingum channel routing for which
La Ecuación 9-1 fue desarrollado en 1938 y se ha utilizado ampliamente desde entonces [11].
Es esencialmente una generalización del concepto de reservorio lineal (Ec. 8-7).
De hecho, para X = 0, la Ec. 9-1 se reduce a la Ec. 8-7.
En otras palabras, el tránsito del reservorio lineal es un caso especial del tránsito del canal
de Muskingum para el cual
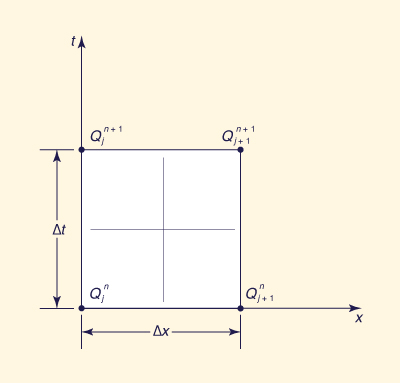
To derive the Muskingum routing equation, Eq. 8-4 is discretized on the x-t plane (Fig. 8-2), to yield Eq. 8-13, repeated here:
Para derivar la ecuación de tránsito de Muskingum, la Ec. 8-4 es discretizado en el plano x-t (Fig. 8-2), a ceder la Ec. 8-13, que se repite aquí:
|
I1 + I2 O1 + O2 S2 - S1 __________ - ___________ = ___________ 2 2 Δt | (8-13) |
Equation 9-1 is expressed at time levels 1 and 2:
Ecuación 9-1 se expresa en niveles de tiempo 1 y 2:
| S1 = K [ X I1 + ( 1 - X ) O1 ] | (9-2) |
| S2 = K [ X I2 + ( 1 - X ) O2 ] | (9-3) |
Substituting Eqs. 9-2 to 9-3 into Eq. 8-13 and solving for O2 yields Eq. 8-15, repeated here:
Sustituyendo las Ecs. 9-2 a 9-3 en la Ec. 8-13 y despejando para O2 produce la Ec. 8-15, que se repite aquí:
| O2 = C0 I2 + C1 I1 + C2 I1 | (8-15) |
in which C0, C1 and C2 are routing coefficients defined in terms of Δt, K, and X as follows:
en la que C0, C1 y C2 son coeficientes de tránsito definidos en términos de Δ t, K y X de la siguiente manera:
|
( Δt / K ) - 2X C0 = _______________________ 2(1 - X) + ( Δt / K ) | (9-4) |
|
( Δt / K ) + 2X C1 = _______________________ 2(1 - X) + ( Δt / K ) | (9-5) |
|
2(1 - X) - ( Δt / K ) C2 = _______________________ 2(1 - X) + ( Δt / K ) | (9-6) |
Since C0 + C1 + C2 = 1, the routing coefficients may be interpreted as weighting coefficients.
For
Desde C0 + C1 + C2 = 1, los coeficientes de
tránsito pueden ser interpretados como coeficientes de ponderación.
Para
*****1609291016***
Given an inflow hydrograph, an initial flow condition, a chosen time interval Δt, and routing parameters X and K, the routing coefficients can be calculated with Eqs. 9-4 to 9-6, and the outflow hydrograph with Eq. 8-15. The routing parameters K and K are related to flow and channel characteristics, K being interpreted as the travel time of the flood wave from upstream end to downstream end of the channel reach. Therefore, K accounts for the translation (or concentration) portion of the routing (Fig. 9-3).
Dado un hidrograma de entrada de flujo, una condición de flujo inicial, un intervalo de tiempo Δt elegido; y parámetros de tránsito X y K, los coeficientes de tránsito pueden calcularse con las Ecs. 9-4 a 9-6, y el hidrograma de salida de flujo con la Ec. 8-15. Los parámetros de tránsito K y K están relacionados con las características de flujo y canal, K se interpreta como el tiempo de viaje de la onda de flujo del extremo aguas arriba y aguas abajo del tramo del canal. Por lo tanto, K cuenta para la parte de traslado (o concentración) de tránsito (Fig. 9-3).
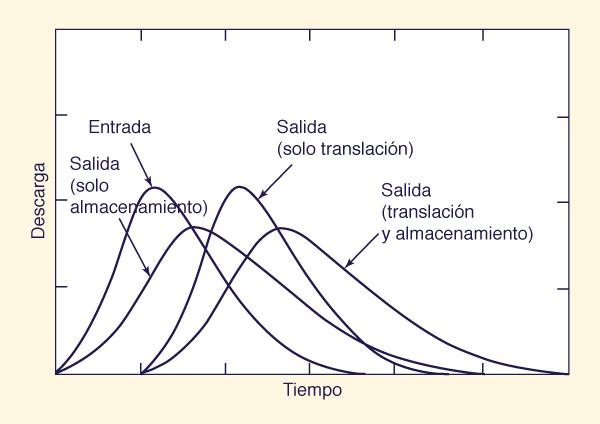
The parameter X accounts for the storage portion of the routing. For a given flood event, there is a value of X for which the storage in the calculated outflow hydrograph matches that of the measured outflow hydrograph. The effect of storage is to reduce the peak flow and spread the hydrograph in time (Fig. 9-4). Therefore, it is often used interchangeably with the terms diffusion and peak attenuation.
El parámetro X representa la parte de almacenamiento de tránsito. Para un evento de inundación dado, existe un valor de X para los que el almacenamiento en el hidrograma de flujo de salida calculada coincide con la del hidrograma de salida medido. El efecto del almacenamiento es reducir el flujo máximo y difundir el hidrograma en el tiempo (Fig. 9-4). Por lo tanto, se utiliza a menudo de manera intercambiable con los términos difusión y la atenuación de pico.
Figure 9-4 Translation and storage processes in stream channel routing./ Procesos de traslado y almacenamiento en el tránsito de canal de flujo. |
The routing parameter K is a function of channel reach length and flood wave speed; conversely, the parameter X is a function of the flow and channel characteristics that cause runoff diffusion. In the Muskingum method, X is interpreted as a weighting factor and restricted in the range 0.0 ≤ X ≤ 0.5. Values of X greater than 0.5 produce hydrograph amplification (i.e., negative diffusion), which does not correspond with reality (under the Froude numbers applicable to flood flows). With K = Δt and X = 0.5, flow conditions are such that the outflow hydrograph retains the same shape as the inflow hydrograph, but it is translated downstream a time equal to K. For X = 0, Muskingum routing reduces to linear reservoir routing (Section 8.2).
El parámetro de tránsito K es una función de la longitud del tramo del canal y la velocidad de onda de flujo; por el contrario, el parámetro X es una función de las características de flujo y del canal que causan la difusión de escorrentía. En el método de Muskingum, X se interpreta como un factor de ponderación y restringido en el rango 0.0 ≤ X ≤ 0.5. Los valores de X mayores de 0.5 produce una amplificación del hidrograma (es decir, difusión negativa), que no se corresponde con la realidad (bajo los números de Froude aplicables a los flujos de inundación). Con K = Δt y X = 0.5, las condiciones de flujo son tales que el hidrograma de salida conserva la misma forma que el hidrograma de entrada de flujo, pero trasladan aguas abajo a un tiempo igual a K. Para X = 0, el tránsito de Muskingum se reduce al tránsito del reservorio lineal (Sección 8.2).
In the Muskingum method, the parameters K and X are determined by calibration using streamflow records. Simultaneous inflow-outflow discharge measurements for a given channel reach are coupled with a trial-and-error procedure, leading to the determination of K and X (see Example 9-2). The procedure is time-consuming and lacks predictive capability. Values of K and X determined in this way are valid only for the given reach and flood event used in the calibration. Extrapolation to other reaches or to other flood events (of different magnitude) within the same reach is usually unwarranted.
En el método de Muskingum, los parámetros K y X se determinan por calibración usando los registros de caudales. Las mediciones de las descargas de entrada-salida de flujo simultáneas para un tramo de canal dado se acoplan con un procedimiento de prueba y error, lo que lleva a la determinación de K y X (véase el Ejemplo 9-2). El procedimiento es lento y carece de capacidad de predicción. Los valores de K y X determinados en esta forma son válidos sólo para el tramo dado y el evento de inundación utilizado en la calibración. La extrapolación a otros tramos o para otros eventos de inundación (de diferente magnitud) dentro del mismo alcance suele ser injustificada.
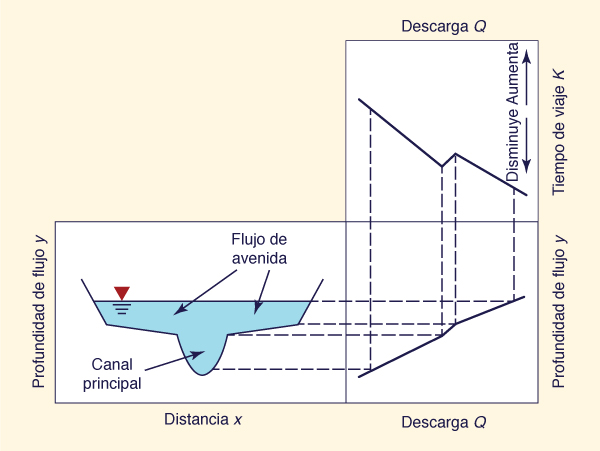
When sufficient data are available, a calibration can be performed for several flood events, each of different magnitude, to cover a wide range of flood levels. In this way, the variation of K and X as a function of flood level can be ascertained. In practice, K is more sensitive to flood level than X. A sketch of the variation of K with stage and discharge is shown in Fig. 9-5.
Cuando se dispone de datos suficientes, la calibración se puede realizar por varios eventos de inundación, cada uno de diferente magnitud, para cubrir una amplia gama de niveles de inundación. De esta manera, la variación de K y X como una función del nivel de inundación puede ser comprobada. En la práctica, K es más sensible al nivel de inundación que X. Se muestra un bosquejo de la variación de K con el nivel y la descarga en la Fig. 9-5.
Figure 9-5 Bosquejo de tiempo de viaje en función de la descarga y la etapa. |
****1610111515****
Example 9-1./ Ejemplo 9-1.
An inflow hydrograph to a channel reach is shown in Col. 2 of Table 9-1.
Assume baseflow is 352 m3/s.
Using the Muskingum method, route this hydrograph through a channel reach with K = 2 d and X = 0.1 to calculate an outflow hydrograph.
Un hidrograma de entrada de flujo a un tramo de canal se muestra en la Col. 2 de la Tabla 9-1. Supóngase un flujo de base es de 352 m3/s. Utilizando el método de Muskingum, transita este hidrograma a través de un tramo del canal con K = 2 d y X = 0.1 para calcular un hidrograma de salida de flujo.
First, it is necessary to select a time interval Δt.
In this case, it is convenient to choose Δt = 1 d. As with reservoir routing, the ratio of time-to-peak to time interval (tp/Δt) should be greater than or equal to 5.
In addition, the chosen time interval should be such that the routing coefficients remain positive.
With Δt = 1 d, K = 2 d, and X = 0.1, the routing coefficients (Eqs. 9-4 to 9-6) are: C0 = 0.1304; C1 = 0.3044; and C2 = 0.5652.
It is verified that C0 + C1 + C2 = 1.
The routing calculations are shown in Table 9-1.
En primer lugar, es necesario seleccionar un intervalo de tiempo Δt.
En este caso, es conveniente elegir Δt = 1 d. Como con el tránsito del reservorio, la relación de tiempo-a-pico al intervalo de tiempo
(tp/Δt) debe ser mayor que o igual a 5.
Además, el intervalo de tiempo elegido debe ser tal que los coeficientes de tránsito siguen siendo positivos. Con Δt = 1 d, K = 2 d, and X = 0.1, los coeficientes de enrutamiento (Ecuaciones 9-4 a 9-6) son: C0 = 0.1304; C1 = 0.3044; y C2 = 0.5652. Se verifica que C0 + C1 + C2 = 1.
Los cálculos de tránsito se muestran en la Tabla 9-1.
***1610131640*** Column 1 shows the time in days.
La Columna 1 muestra el tiempo en días.
Column 2 shows the inflow hydrograph ordinates in cubic meters per second.
La Columna 2 muestra las ordenadas del hidrograma de flujo de entrada en metros cúbicos por segundo.
Columns 3-5 show the partial flows.
Las Columnas 3-5 muestran los flujos parciales.
Following Eq. 8-15, Cols. 3-5 are summed to obtain Col. 6, the outflow hydrograph ordinates in cubic meters per second.
Después de la Ec. 8-15, las Cols. 3-5 se suman para obtener la Col. 6, las ordenadas
del hidrograma de salida en metros cúbicos por segundo.
To explain the procedure briefly, the outflow at the start (day 0) is assumed to be equal to the inflow at the start: 352 m3/s. The inflow at day 1 multiplied by C0 is entered in Col. 3, day 1: 76.6 m3/s.
The inflow at day 0 multiplied by C1 is entered in Col. 4, day
1: 107.1 m3/s. The outflow at day 0 multiplied by C2 is entered in Col. 5, day 1: 199 m3/s. Columns 3-5 of day 1 are summed to obtain Col. 6 of day 1: 76.6 + 107.1 + 199.0 = 382.7 m3/s. The calculations proceed in a recursive manner until all outflows in Col. 6 have been obtained.
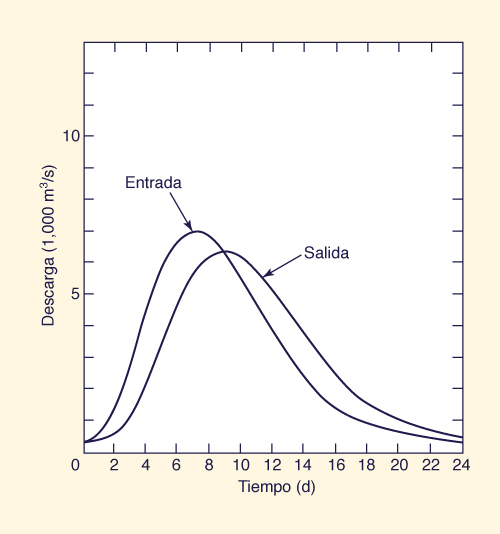
Inflow and outflow hydrographs are plotted in Fig. 9-6.
The outflow peak is 6352.6 m3/s, which shows that the inflow peak, 6951 m3/s, has attenuated to about 91 % of its initial value.
The peak outflow occurs at day 9, 2 d after the peak inflow, which occurs at day 7.
The time elapsed between the occurrence of peak inflow and peak outflow is generally equal to K, the travel time.
Para explicar el procedimiento brevemente, el flujo de salida en el inicio (día 0) se supone que es igual al flujo de entrada en el inicio: 352 m3/s. El flujo de entrada en el día 1 multiplicado por
C0 por C0 se introduce en la Col. 3, día 1:
76.6 m3/s. El flujo de entrada en el día 0 multiplicado por C1 se introduce en la Col. 4, día 1: 107.1 m3/s.
El flujo de salida en el día 0 multiplicado por C2 se introduce en la Col. 5, día 1:
199 m3/s. Columnas 3-5 del día 1 se suman para obtener las Col. 6 del día 1:
76.6 + 107.1 + 199.0 = 382.7 m3/s. Los cálculos se realizan de manera recursiva hasta que se hayan obtenido todos los flujos de salida en la Col. 6.
Los hidrogramas de flujo de entrada y salida se representan gráficamente en la Fig. 9-6.
El pico de flujo de salida es 6352.6 m3/s, lo que demuestra que el pico de
flujo de entrada, 6951 m3/s, ha atenuado hasta alrededor de 91% de su valor inicial.
El pico de flujo de salida se produce en el día 9, 2 d después de que el pico de flujo de entrada, que se produce en el día 7. El tiempo transcurrido entre la aparición del pico de flujo de entrada y el pico
de flujo de salida es generalmente igual a K, el tiempo de viaje.
ONLINE CALCULATION.
Using ONLINE ROUTING04, the answer
is essentially the same as that of Col. 6, Table 9-1
ONLINE CALCULATION.
Usando ONLINE ROUTING04,
ROUTING04 EN LÍNEA, la respuesta es esencialmente el mismo que el de la Col. 6, Tabla 9-1..
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Figure 9-6 El tránsito del canal de flujo por el método de Muskingum: Ejemplo 9-1. |
Unlike reservoir routing, stream channel-routing calculations exhibit a definite (time) lag between inflow and outflow. Furthermore, in the general case (X ≠ 0), maximum outflow does not occur at the time when inflow and outflow coincide.
A diferencia del tránsito del reservorio, los cálculos del tránsito del canal de flujo presentan un definido (tiempo) de retraso entre el flujo de entrada y salida. Además, en el caso general (X ≠ 0), el máximo flujo de salida no se produce en el momento cuando coincide el flujo de entrada y salida.
Example 9-1 has illustrated the predictive stage of the Muskingum method, in which the routing parameters are known in advance of the routing. If the parameters are not known, it is first necessary to perform a calibration. The trial-and-error procedure to calibrate the routing parameters is illustrated by Example 9-2.
El Ejemplo 9-1 se ha ilustrado la etapa de predicción del método Muskingum, en el que se conocen los parámetros de tránsito antes del tránsito. Si no se conocen los parámetros, es necesario primero realizar una calibración. El procedimiento de prueba y error para calibrar los parámetros de tránsito se ilustra en el Ejemplo 9-2.
Example 9-2. / Ejemplo 9-2.
Use the outflow hydrograph calculated in the previous example together with the given
inflow hydrograph to calibrate the Muskingum method, that is, to find the routing parameters K and X.
Utilice el hidrograma de salida calculado en el ejemplo anterior, junto con el hidrograma de flujo de entrada dado para calibrar el método de Muskingum, es decir, para encontrar los parámetros de tránsito
K y X.
The procedure is summarized in Table 9-2.
El procedimiento se resume en la Tabla 9-2.
Column 1 shows the time in days.
La columna 1 muestra el tiempo en días.
Column 2 shows the inflow hydrograph in cubic meters per second.
La Columna 2 muestra el hidrograma de entrada de flujo en metros cúbicos por segundo.
***1610132210*** Column 3 shows the outflow hydrograph in cubic meters per second.
La Columna 3 muestra el hidrograma de salida de flujo en metros cúbicos por segundo.
Column 4 shows the channel storage in (cubic meters per second)-days.
La Columna 4 muestra el registro de canales en (metros cúbicos por segundo) -días.
Channel storage at the start is assumed to be 0, and this value is entered in Col. 4, day 0.
Almacenamiento de canal en el inicio se supone que es 0, y se introduce este valor en la Col. 4, día 0.
Channel storage is calculated by solving Eq. 8-13 for S2:
El almacenamiento del canal se calcula mediante la resolución de la Ec. 8-13 para S2:
Several values of X are tried, within the range 0.0 to 0.5, for example, 0.1, 0.2 and 0.3.
Varios valores de X se prueban, dentro del rango de 0.0 a 0.5, por ejemplo, 0.1, 0.2 y 0.3.
For each trial value of X, the weighted flows [ XI + ( 1 - X ) O ] are calculated, as shown in Cols. 5-7.
Para cada valor de prueba de X, los flujos ponderados
[ XI + ( 1 - X ) O ] se calculan, como se muestra en Cols. 5-7.
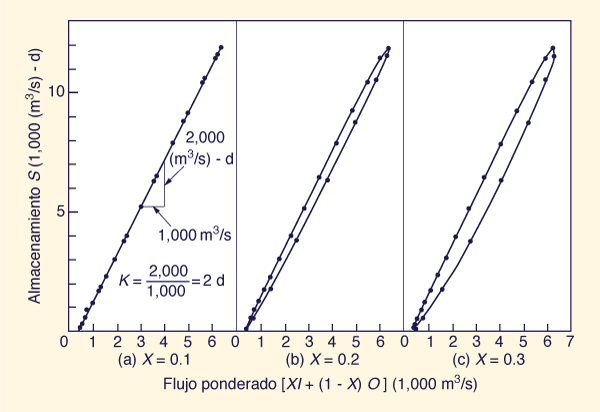
Each of the weighted flows is plotted against channel storage (Col. 4), as shown in Fig. 9-7.
Cada uno de los flujos ponderados se representa en función de almacenamiento de canal (Col. 4), como se muestra en la Fig. 9-7.
The value of X for which the storage versus weighted flow data plots closest to a line is taken as the correct value of X.
In this case, Fig. 9-7 (a): X = 0.1 is chosen.
El valor de X para el cual el almacenamiento frente a gráficos de datos de flujo ponderados más cercanos a una línea se toma como el valor correcto de X. En este caso, la Fig. 9-7 (a):
X = 0.1 se elige.
Following Eq. 9-1, the value of K is obtained from Fig. 9-7 (a) by calculating the slope of the storage vs weighted outflow curve.
Siguiendo la Ec. 9-1, el valor de K se obtiene a partir de la Fig. 9-7 (a) mediante el cálculo de la pendiente de almacenamiento vs la curva del flujo de salida ponderado.
In this case, the value of K = [2000 (m3/s)-d]/(1000 m3/s) = 2 d.
En este caso, el valor de K = [2000 (m3/s)-d]/(1000 m3/s) = 2 d.
Thus, it is shown that K = 2 days and X = 0.1 are the Muskingum routing parameters for the given inflow and outflow hydrographs.
Por lo tanto, se muestra que K = 2 días y X = 0.1 son los parámetros de tránsito de Muskingum para los hidrogramas de flujo de entrada y salida dados.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Figure 9-7 Calibración de parámetros de tránsito de Muskingum: Ejemplo 9-2. |
The estimation of routing parameters is crucial to the application of the Muskingum method. The parameters are not constant, tending to vary with flow rate. If the routing parameters can be related to flow and channel characteristics, the need for trial-and-error calibration would be eliminated. Parameter K could be related to reach length and flood wave velocity, whereas X could be related to the diffusivity characteristics of flow and channel. These propositions are the basis of the Muskingum-Cunge method (Section 9.4).
La estimación de los parámetros de tránsito es crucial para la aplicación del método de Muskingum. Los parámetros no son constantes, que tiende a variar con la velocidad de flujo. Si los parámetros de tránsito pueden estar relacionados con el flujo y las características del canal, la necesidad de calibración de prueba y error serían eliminados. El parámetro K podría estar relacionado con el tramo de longitud y la velocidad de la onda de inundación, mientras que X podría estar relacionado con las características de difusividad de flujo y el canal. Estas proposiciones son la base del método de Muskingum-Cunge (Sección 9.4).
****1610132314***
9.2 ONDAS CINEMÁTICAS
|
|
Three types of unsteady open-channel flow waves are commonly used in engineering
hydrology:
Tres tipos de ondas de flujo inestables en canales abiertos se utilizan comúnmente en la ingeniería
de hidrología:
Ecuación de onda cinemática
The derivation of the kinematic wave equation is based on the principle of mass conservation within a control volume. This principle states that the difference between outflow and inflow within one time interval is balanced by a corresponding change in volume. In terms of finite intervals (i.e., finite differences) it is:
La derivación de la ecuación de onda cinemática se basa en el principio de conservación de la masa dentro de un volumen de control. Este principio establece que la diferencia entre flujo de salida y flujo de entrada dentro de un intervalo de tiempo es equilibrada por un cambio correspondiente en volumen. En términos de intervalos finitos (es decir, diferencias finitas) es:
| ( Q2 - Q1 ) Δt + ( A2 - A1 ) Δx = 0 | (9-8) |
in which Q = flow; A = flow area; Δt = time interval; and Δx = space interval.
In differential form,
en la que Q = flujo; A = área de flujo; Δ t = intervalo de tiempo; y Δ x = intervalo de espacio.
En forma diferencial,
|
∂Q ∂A ____ + ____ = 0 ∂x ∂t | (9-9) |
which is the equation of conservation of mass, or equation of continuity.
que es la ecuación de conservación de la masa, o la ecuación de continuidad.
The equation of conservation of momentum (Eq. 4-22) contains local inertia, convective inertia, pressure gradient (due to flow depth gradient), friction (friction slope), gravity (bed slope), and a momentum source term (Section 4.2). In deriving the kinematic wave equation, a statement of uniform flow is used in lieu of conservation of momentum. Since uniform flow is strictly a balance of friction and gravity, it follows that local and convective inertia, pressure gradient, and momentum source terms are excluded from the formulation of kinematic waves. In other words, a kinematic wave is a simplified wave that does not include these terms or processes. As shown later in this section, this simplification imposes limits to the applicability of kinematic waves.
La ecuación de conservación del momento (Ec. 4-22) contiene la inercia local, inercia convectiva, gradiente de presión (debido al flujo gradiente de profundidad), fricción (pendiente de fricción), la gravedad (pendiente del lecho), y un término fuente de momento (Sección 4.2 ). Al derivar la ecuación de onda cinemática, un estado de flujo uniforme se utiliza en lugar de la conservación del momento. Dado que el flujo uniforme es estrictamente un equilibrio de la fricción y de la gravedad, se deduce que la inercia local y convectiva, gradiente de presión, y los términos de la fuente de momento se excluyen de la formulación de las ondas cinemáticas. En otras palabras, una onda cinemática es una onda simplificada que no incluye estos términos o procesos. Como se muestra más adelante en esta sección, esta simplificación impone límites a la aplicabilidad de la onda cinemática.
Uniform flow in open channels is described by the Manning or Chezy formulas (Section 2.4). The Manning equation is:
El flujo uniforme en canales abiertos se describe por las fórmulas de Manning o Chezy (Sección 2.4). La ecuación de Manning es:
|
1 Q = ___ A R 2/3 Sf 1/2 n | (9-10) |
in which R is the hydraulic radius in meters, Sf is the friction slope in meters per meter, and n is the Manning friction coefficient. A pictorial on n is given by Barnes (1967).
en la que R es el radio hidráulico en metros, Sf es la pendiente de fricción en metros por metro, y n es el coeficiente de fricción Manning. Una pictórica en n es dada por Barnes (1967) .
The Chezy equation is:
La ecuación de Chezy es:
|
Q = C A R 1/2 Sf 1/2 | (9-11) |
in which C = Chezy coefficient. Notice that in unsteady flow, friction slope is used in Eqs. 9-10 and 9-11 in lieu of channel slope.
en la que C = coeficiente de Chezy. Nótese que en el flujo no permanente, la pendiente de fricción se usa en las Ecs. 9-10 y 9-11 en lugar de la pendiente del canal.
The hydraulic radius is R = A / P , in which P is the wetted perimeter. Substituting this into Eq. 9-10, leads to:
El radio hidráulico es R = A/P, en el que P es el perímetro mojado. Sustituyendo esto en la Ec. 9-10, conduce a:
|
1 Sf 1/2 Q = ___ _________ A5/3 n P 2/3 | (9-12) |
Assume for the sake of simplicity that n, Sf, and P are constant. This may be the case of a wide channel in which P can be assumed to be essentially independent of A. Equation 9-12 can then be written as:
Suponga que en aras de la simplicidad que n, Sf y P son constantes. Este puede ser el caso de un canal amplio en el que P se puede suponer que sea esencialmente independiente de A. La Ecuación 9-12 entonces se puede escribir como:
| Q = α Aβ | (9-13) |
in which α and β are parameters of the discharge-area rating (see rating curve, Section 2.4), defined as follows:
en la que α y β son los parámetros de la velocidad del área de descarga (véase la curva de gastos, Sección 2.4), que se define de la siguiente manera:
|
1 Sf 1/2 α = ___ _________ n P 2/3 | (91-4) |
|
5 β = ___ 3 | (9-15) |
In Eq. 9-13, differentiating Q with respect to A leads to:
En la Ec. 9-13, diferenciando Q con respecto a A lleva a:
|
dQ Q _____ = β ____ = β V dA A | (9-16) |
in which V is the mean flow velocity.
en la que V es la velocidad media del flujo.
Multiplying Eqs. 9-9 and 9-16 and applying the chain rule, the kinematic wave equation is obtained:
Multiplicando las Ecs. 9-9 y 9-16 y aplicando la regla de la cadena, la ecuación de onda cinemática se obtiene:
|
∂Q dQ ∂Q _____ + (_____) ______ = 0 ∂t dA ∂x | (9-17) |
or, alternatively
o alternativamente
|
∂Q ∂Q _____ + (β V) ______ = 0 ∂t ∂x | (9-18) |
Equation 9-17 (or 9-18) describes the movement of waves which are kinematic in nature . These are referred to as kinematic waves, i.e., waves for which inertia and pressure (flow depth) gradient have been neglected [10]. Equation 9-17 is a first-order partial differential equation. Therefore, kinematic waves travel with wave celerity dQ/dA (or βV) and do not attenuate. Wave attenuation can only be described by a second-order partial differential equation.
La Ecuación 9-17 (o 9-18) describe el movimiento de las ondas que son cinemáticas en la naturaleza. Estos se conocen como ondas cinemáticas, es decir, las ondas para las que el gradiente de inercia y presión (profundidad de flujo) han sido olvidadas [10]. La ecuación 9-17 es una ecuación diferencial parcial de primer orden. Por lo tanto, las ondas cinemáticas viajan con celeridad de la onda dQ/dA (o βV) y no se atenuen. La onda de atenuación sólo puede ser descrito por una ecuación diferencial parcial de segundo orden.
The absence of wave attenuation can be further explained by resorting to a mathematical argument. Since dQ/dA is the celerity of the unsteady (i.e. , wavelike) Q, it can be replaced by dx/dt. Therefore, in Eq. 9-17:
La ausencia de atenuación de la onda se explica aún más por recurrir a un argumento matemático. Desde dQ/dA es la celeridad de la inestable (es decir, en forma de onda) Q, que puede ser sustituido por dx/dt. Por lo tanto, en la Ec. 9-17:
|
∂Q dx ∂Q _____ + (_____) ______ = 0 ∂t dt ∂x | (9-19) |
which is equal to the total derivative dQ/dt. Since the right side of Eq. 9-19 is zero, it follows that Q remains constant in time for waves traveling with celerity dQ/dA.
que es igual a la derivada total dQ/dt. Desde el lado derecho de la Ec. 9-19 es cero, se deduce que Q se mantiene constante en el tiempo para las ondas que viajan con celeridad dQ/dA.
Discretización de la ecuación de onda cinemática
Equation 9-18 (or 9-17) is a nonlinear first-order partial differential equation describing the change of discharge Q in time and space. It is nonlinear because the wave celerity βV (or dQ/dA) varies with discharge. The nonlinearity, however, is usually mild, and therefore, Eq. 9-18 can also be solved in a linear mode by considering the wave celerity to be constant.
La ecuación 9-18 (o 9-17) es una ecuación diferencial parcial de primer orden no lineal que describe el cambio de la descarga Q en el tiempo y el espacio. Es no lineal debido a la celeridad de la onda βV (o dQ/dA) varía con la descarga. La no linealidad, sin embargo, es generalmente leve, y por lo tanto, la Ec. 9-18 también se puede resolver de un modo lineal, considerando la celeridad de la onda ser constante.
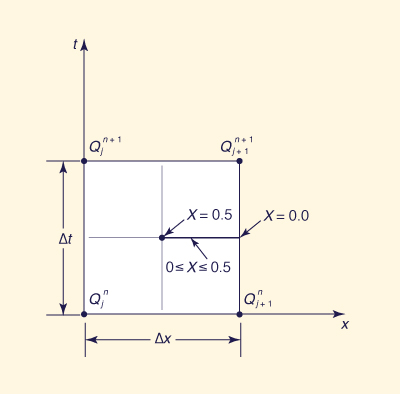
The solution of Eq. 9-18 can be obtained by analytical or numerical means. The simplest kinematic wave solution is a linear numerical solution. For this purpose, it is necessary to select a numerical scheme with which to discretize Eq. 9-18 on the x-t plane (Fig. 9-8). A review of basic concepts of numerical analysis is necessary before discussing numerical schemes.
La solución de la Ec. 9-18 se puede obtener por medios analíticos o numéricos. La solución más simple de onda cinemática es una solución numérica lineal. Para este propósito, es necesario seleccionar un esquema numérico con el que discretizar la Ec. 9-18 en el x-t plano (fig. 9-8). Una revisión de los conceptos básicos del análisis numérico es necesaria antes de discutir los esquemas numéricos.
Figure 9-8 Space-time discretization of kinematic wave equation. |
Order of Accuracy of Numerical Schemes. The order of accuracy of a numerical scheme measures the ability of the scheme to reproduce (i.e., recreate) the terms of the differential equation. In general, the higher the order of accuracy of a scheme, the better it is able to reproduce the terms of the differential equation. Forward and backward finite differences have first-order accuracy, i.e., discretization errors of first order. Central differences have second-order accuracy, with discretization errors of second order.
Grado de Exactitud de los Esquemas Numéricos. El orden de exactitud de un esquema numérico mide la capacidad del sistema para reproducir (es decir, recrear) los términos de la ecuación diferencial. En general, cuanto mayor sea el grado de exactitud de un esquema, mejor es capaz de reproducir los términos de la ecuación diferencial. Reenviar y hacia atrás las diferencias finitas tienen exactitud de primer orden, es decir, los errores de discretización de primer orden. Las diferencias centrales tienen una precisión de segundo orden, con errores de discretización de segundo orden.
When solving Eq. 9-18 by numerical methods, first-order schemes create numerical diffusion and numerical dispersion, while second-order schemes create only numerical dispersion. A third-order scheme creates neither numerical diffusion nor dispersion. Numerical diffusion and/or dispersion are caused by the finite grid size and are not necessarily related to the physical problem.
Al resolver la Ec. 9-18 por métodos numéricos, los esquemas de primer orden crean difusión numérica y la dispersión numérica, mientras que los sistemas de segundo orden sólo crean la dispersión numérica. Un esquema de tercer orden crea ni difusión numérica ni la dispersión. La difusión numérica y/o dispersión son causados por el tamaño de la rejilla finita y no están necesariamente relacionados con el problema físico.
Second-order-accurate Numerical Scheme. The discretization of Eq. 9-18 following a linear second-order-accurate scheme, i.e., using central differences in space and time, leads to (Fig. 9-8):
Esquema Numérico de Segundo Orden de Precisión. La discretización de la Ec. 9-18 siguiendo un esquema de segundo orden de precisión lineal, es decir, mediante las diferencias centrales en el espacio y el tiempo, conduce a (Figura 9-8.):
|
M N ______ + βV ______ = 0 Δt Δx | (9-20) |
|
Q j+1n+1 + Q j n+1 Q j+1n + Q j n M = ___________________ - _________________ 2 2 | (9-20a) |
|
Q j+1n + Q j+1 n+1 Q j n + Q j n+1 N = ___________________ - _________________ 2 2 | (9-20b) |
in which βV has been held constant (linear mode), leading to:
en la que βV se ha mantenido constante (modo lineal), lo que lleva a:
| Q j+1 n+1 = C0 Q j n+1 + C1 Q j n + C2 Q j+1 n | (9-21) |
en el cual
|
C - 1 C0 = _______ 1 + C | (9-22) |
| C1 = 1 | (9-23) |
|
1 - C C2 = _______ 1 + C | (9-24) |
and C is the Courant number, defined as follows:
y C es el número de Courant, que se define de la siguiente manera:
|
Δt C = βV _____ Δx | (9-25) |
Note that Courant number is the ratio of physical wave celerity βV to grid celerity Δx /Δt. The Courant number is a fundamental concept in the numerical solution of hyperbolic partial differential equations.
Nótese que el número de Courant es la relación de la celeridad de la onda física βV para la celeridad de rejilla Δx /Δt. El número de Courant es un concepto fundamental en la solución numérica de ecuaciones diferenciales parciales hiperbólicas.
Example 9-3.
Use Eq. 9-21 with the routing coefficients of Eqs. 9-22 to 9-24 (linear kinematic wave numerical solution using central differences in space and time) to route the following triangular flood wave.
Consider the following three cases: (1) V = 1.2 m/s and Δx = 7200 m; (2) V = 1.2 m/s and Δx = 4800 m; and (3) V = 0.8 mls and Δx = 4800 m. Use β = 5/3, and Δt = 1 h.
Utilice la Ec. 9-21 con los coeficientes de tránsito de las Ecs. 9-22 a 9-24 (solución numérica de la onda cinemática lineal utilizando diferencias centrales en espacio y tiempo) para dirigir la siguiente onda de flujo triangular.
Tenga en cuenta los siguientes tres casos: (1)V = 1.2 m/s and Δx = 7200 m; (2) V = 1.2 m/s and Δx = 4800 m; y (3) V = 0.8 mls y Δx = 4800 m. Usar β = 5/3, y Δt = 1 h.
Using Eq. 9-25: C = 1.
Using Eqs. 9-22 to 9-24: C0 = 0; C1 = 1; C2 = 0.
The routing by Eq. 9-21 shown in Table 9-3 depicts the pure translation of the hydrograph a time equal to Δt.
In other words, for βV = Δx/Δt (i.e., C = 1), the central difference scheme is of third order, and the numerical solution is exactly equal to the analytical solution.
Utilizando la Ec. 9-25: C = 1.
Usando las Ecs. 9-22 a 9-24: C0 = 0; C1 = 1; C2= 0.
El tránsito para la Ec. 9-21 se muestra en la Tabla 9-3 representa la traducción pura del hidrograma un tiempo igual a
Δt.
En otras palabras, por βV = Δx/Δt (es decir, C = 1 ), el esquema de diferencia central es de tercer orden, y la solución numérica es exactamente igual a la solución analítica.
Using Eq. 9-25: C = 1.5.
Using Eqs. 9-22 to 9-24: C0 = 0.2; C1 = 1.0; C2 = -0.2.
The routing by Eq. 9-21 shown in Table 9-4 depicts the translation of the hydrograph a time approximately equal to Δt, but it also shows a small amount of numerical dispersion because βV
is not equal to Δx/Δt.
The dispersion, including the notorious negative
outflows at the trailing end of the hydrograph, are caused by errors associated with the scheme's second-order accuracy.
Utilizando la Ec. 9-25: C = 1.5.
Utilizando las Ecs. 9-22 a 9-24: C0 = 0,2; C1 = 1.0; C2 = -0.2.
El tránsito para la Ec. 9-21 se muestra en la Tabla 9-4 representa la traducción del hidrograma un tiempo aproximadamente igual a Δt, sino que también muestra una pequeña cantidad de dispersión numérica porque βV
no es igual a Δx/Δt.
La dispersión, incluyendo los notorios flujos de salida negativos en el extremo posterior del hidrograma, son causadas por errores asociados con una precisión de segundo orden del esquema.
Using Eq. 9-25, C = 1.
Therefore, the solution is the same as in the first case, exhibiting pure hydrograph translation.
Utilizando la Ec. 9-25, C=1.
Por lo tanto, la solución es el mismo que en el primer caso, exhibiendo la traducción del hidrograma puro.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The three cases of Example 9-3 illustrate the properties of kinematic waves. The second-order-accurate scheme has no numerical diffusion. In addition, for Courant number C = 1, i.e., the wave celerity βV equal to the grid celerity Δx/Δt, the scheme has no numerical dispersion, with the hydrograph being translated downstream without change in shape. In other words, the numerical solution by Eqs. 9-21 to 9-25 is exact only for Courant number C = 1. For other values of C, the numerical solution exhibits perceptible amounts of numerical dispersion.
Los tres casos del Ejemplo 9-3 ilustran las propiedades de las ondas cinemáticas. El esquema de segundo orden con precisión no tiene difusión numérica. Además, para el número de Courant C = 1, es decir, la celeridad de la onda βV igual a la celeridad de rejilla y Δx/Δt, el esquema no tiene dispersión numérica, con el hidrograma siendo trasladado aguas abajo sin cambio de forma. En otras palabras, la solución numérica de las Ecs 9-21 a 9-25 es exacta sólo por número de Courant C = 1. Para otros valores de C, la solución numérica exhibe cantidades perceptibles de dispersión numérica.
First-order-accurate Numerical Scheme. / Esquema Numérico de Primer Orden con Precisión.
The numerical solution of Eq. 9-18 can also be attempted using a first-order-accurate scheme, i.e., one featuring forward or backward finite differences. The discretization of Eq. 9-18 in a linear mode, using backward differences in both space and time yields (Fig. 9-8):
La solución numérica de la Ec 9-18 también se puede intentar usar un esquema de primer orden con precisión, es decir, uno que ofrece hacia adelante o hacia atrás diferencias finitas. La discretización de la Ec. 9-18 en un modo lineal, utilizando las diferencias hacia atrás en tanto los rendimientos de espacio y tiempo (Fig. 9-8):
|
Q j+1n+1 - Q j+1 n Q j+1n+1 - Q j n+1 ____________________ + βV ___________________ = 0 Δt Δx | (9-26) |
a partir del cual
| Q j+1n+1 = C0 Q j n+1 + C2 Q j+1n | (9-27) |
en el cual
|
C C0 = _________ 1 + C | (9-28) |
|
1 C2 = _________ 1 + C | (9-29) |
and C = Courant number, defined by Eq. 9-25.
y C= número de Courant, que se define por la Ec. 9-25.
Example 9-4.
Use Eq. 9-27 with the coefficients calculated by Eq. 9-28 and 9-29 to route the same inflow hydrograph as in the previous example.
Use V = 1.2 m/s; Δx = 7200 m; β = 5/3; and Δt = 1 h.
Utilizar la Ec. 9-27 con los coeficientes calculados por la Ec. 9-28 y 9-29 para transitar el mismo hidrograma de
flujo de entrada como en el ejemplo anterior.
Utilizar V = 1.2 m/s; Δx = 7200 m; β = 5/3; y &Delta y;t = 1 h.
Using Eq. 9-25, C = 1.
Therefore, C0 = 0.5, and C2 = 0.5.
The routing using Eq. 9-27 is shown in Table 9-5.
It is observed that off-centering the derivatives by using backward differences has caused a significant amount of numerical diffusion, with peak outflow of 120.93 m3/s as compared to peak inflow of 150 m3/s.
The conclusion is that different schemes for solving Eq. 9-18 lead to different answers, depending on the time and space intervals, Courant number, order of accuracy of the scheme, and associated numerical diffusion and/or dispersion.
Utilizando la Ec. 9-25, C = 1.
Por lo tanto, C0 = 0.5, y C2 = 0.5.
El tránsito utilizando la Ec. 9-27 se muestra en la Tabla 9-5.
Se observa que el descentramiento de losderivados mediante el uso de las diferencias hacia atrás ha causado una cantidad significativa de difusión numérica, con el pico de flujo de salida de
120.93 m3/s en comparación con el flujo de entrada máxima de 150 m3/s.
La conclusión es que los esquemas diferentes para resolver la Ec. 9-18 conducen a respuestas diferentes, en función de los intervalos de tiempo y espacio, número de Courant, el orden de exactitud del sistema, y la difusión numérica asociada y / o de dispersión.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Convex Method. The convex method of stream channel routing belongs to the family of linear kinematic wave methods. Through the 1970s, it was part of the SCS TR-20 model for hydrologic simulation (Chapter 13). The routing equation for the convex method is obtained by discretizing Eq. 9-18 in a linear mode using a forward-in-time, backward-in-space finite difference scheme, to yield (Fig. 9-8):
Método convexo. El método convexo del tránsito del canal de flujo pertenece a la familia de los métodos de onda cinemática lineal. A través de la década de 1970, fue parte del modelo SCS TR-20 para la simulación hidrológica (Capítulo 13). La ecuación de tránsito para el método convexo se obtiene por discretización de la Ec. 9-18 en un modo lineal utilizando un adelanto en el tiempo, un esquema de diferencias finitas hacia atrás en el espacio, para ceder (Figura 9-8.):
|
Q j+1n+1 - Q j+1n Q j+1n - Q j n __________________ + βV ________________ = 0 Δt Δx | (9-30) |
a partir del cual
| Q j+1n+1 = C1 Q j n + C2 Q j+1n | (9-31) |
en el cual
| C1 = C | (9-32) |
| C2 = 1 - C | (9-33) |
and C = Courant number (Eq. 9-25), restricted to C ≤ 1 for numerical stability reasons. In the convex method, C is regarded as an empirical routing coefficient. Example 9-5 illustrates the application of the convex method.
y C = número de Courant (Ec. 9-25), limitada a C ≤ 1 por razones de estabilidad numérica. En el método convexa, C es considerado como un coeficiente de tránsito empírico. Ejemplo 9-5 ilustra la aplicación del método convexa.
The convex method is relatively simple, but the solution is dependent on the routing parameter C. The latter could be interpreted as a Courant number and related to kinematic wave celerity and grid size, as in Eq. 9-25. However, for values of C other than 1, the amount of diffusion introduced in the numerical problem is unrelated to the true diffusion, if any, of the physical problem. Therefore, the convex method, as well as all kinematic wave methods featuring uncontrolled amounts of numerical diffusion, are regarded as a somewhat crude approach to stream channel routing.
El método convexa es relativamente simple, pero la solución depende del parámetro de tránsito C .
Este último podría ser interpretado como un número de Courant y relacionados
para la celeridad de onda cinemática y el tamaño de la rejilla, como en la Ec. 9-25.
Sin embargo, para valores de C distinto de 1, la cantidad de difusión introducido en el problema numérico no está relacionada con la verdadera difusión, en su caso, del problema físico. Por lo tanto, el método convexo, así como todos los métodos de onda cinemática que ofrecen cantidades incontroladas de difusión numérica, se consideran como un enfoque algo tosco para el tránsito del canal de flujo.
Example 9-5.
Use Eq. 9-31 (the convex method) to route the same inflow hydrograph as in Example 9-3.
Assume C = 2/3.
Utilizando la Ec. 9-31 (el método convexo) para tránsito del mismo hidrograma de flujo de entrada como en el Ejemplo 9-3.
Supongamos que C = 2/3.
The routing coefficients are C1 = C = 2/3; and C2 = 1 - C = 1/3.
The routing is shown in Table 9-6. The convex method leads to a significant amount of diffusion, with peak outflow of 135.06 m3/s as compared to peak inflow of 150 m3/s.
The calculated diffusion amount is a function of C, with practical values of C being restricted in the range 0.5 to 0.9. For C = 1, the hydrograph is translated with no diffusion or dispersion, as in the first and third parts of Example 9-3.
Values of C > 1 render the calculation unstable (large negative values of discharge) and are,
therefore, not recommended.
It should be noted that the instability of the convex method for C > 1 has a parallel in the instability of the Muskingum method for X > 0.5.
Los coeficientes de tránsito son C 1 = C = 2/3; y C 2 = 1 - C = 1/3.
El tránsito se muestra en la Tabla 9-6. El método convexo lleva a una cantidad significativa de difusión, con el flujo de salida pico de 135.06 m3/s, en comparación con el flujo de entrada máxima de 150 m3/s. La cantidad de difusión calculada es una función de C, con valores prácticos de C en proceso de restricción en el rango de 0.5 a 0.9.
Para C = 1, el hidrograma se traslada sin difusión o dispersión, como en las partes primera y tercera del Ejemplo 9-3.
Los valores de C > 1 hacen el cálculo inestables (grandes valores negativos de descarga) y son,
por lo tanto, no se recomienda.
Cabe señalar que la inestabilidad del método convexa para C > 1 tiene un paralelo en la inestabilidad del método de Muskingum para X > 0.5.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Kinematic Wave Celerity
The kinematic wave celerity is dQ/dA, or βV. A value of β = 5/3 was derived for the case of a hydraulically wide channel governed by Manning friction. The kinematic wave celerity is also known as the Kleitz-Seddon, or Seddon, law [8, 19]. In 1900, Seddon [19] published a paper in which he studied the nature of unsteady flow movement in rivers and concluded that the celerity of long disturbances was equal to: Celeridad de Onda Cinemática
La celeridad de onda cinemática es dQ/ dA o β V. Un valor de β = 5/3 se deriva para el caso de un canal amplio hidráulicamente rige por fricción de Manning. La celeridad de onda cinemática también se conoce como el Kleitz-Seddon, o Seddon, la ley [8, 19]. En 1900, Seddon [19] publicó un artículo en el que estudió la naturaleza del movimiento del flujo no permanente en los ríos y llegó a la conclusión de que la celeridad de perturbaciones largas era igual a:
|
1 dQ c = ____ _____ T dy | (9-34) |
in which dQ/dy = slope of the discharge-stage rating (Q versus y), and T = stage, or water surface elevation. The quantity c is the kinematic wave celerity.
en la que dQ/dy = pendiente de la velocidad de la etapa de descarga (Q versus y), y T = etapa, o elevación superficial del agua. La cantidad c es la celeridad de la onda cinemática.
Since dA = T dy, the kinematic wave celerity is equal to dQ/dA (see Eq. 9-17) [10].
Desde dA = T dy , la celeridad de la onda cinemática es igual a dQ/dA (Véase la Ec. 9-17) [10].
From Eq. 9-34 it is concluded that the kinematic wave celerity is a function of the slope of the discharge-stage rating. This slope is likely to vary with stage; therefore, the kinematic wave celerity is not constant but varies with stage and flow level. If c = βV is a function of Q, then Eq. 9-18 is a nonlinear equation requiring an iterative solution. Nonlinear kinematic wave solutions account for the variation of kinematic wave celerity with stage and flow level. The simpler linear solutions, as in Examples 9-3 and 9-4, assume a constant value of kinematic wave celerity βV. Notice that there is a striking similarity between the linear kinematic wave solutions and the Muskingum method. This subject is further examined in Section 9.4.
De la Ec. 9-34 se concluye que la celeridad de la onda cinemática es una función de la pendiente de la velocidad de la etapa de descarga. Esta pendiente es probable que varíe con la etapa; por lo tanto, la celeridad de la onda cinemática no es constante, sino que varía con la etapa y el nivel de flujo. Si c = βV es una función de Q, entonces la Ec. 9-18 es una ecuación no lineal que requiere una solución iterativa. Las soluciones de onda cinemática no lineales en cuenta la variación de la celeridad de la onda cinemática con la etapa y el nivel de flujo. Las soluciones lineales más simples, como en los Ejemplos 9-3 y 9-4, suponen un valor constante de la celeridad de la onda cinemática βV. Observe que hay una similitud sorprendente entre las soluciones de onda cinemática lineal y el método de Muskingum. Este tema se examina más adelante en la Sección 9.4.
Theoretical β values other than 5/3 can be obtained for other friction formulations and cross-sectional shapes. For turbulent flow governed by Manning friction, β has an upper limit of 5/3, and it is usually greater than 1. For laminar flow in wide channels, β = 3; for mixed or transitional flow-between laminar and turbulent Manning, it is in the range 5/3 < β < 3. For flow in a hydraulically wide channel described by the Chezy formula, β = 3/2 (Section 4.2). The calculation of β as a function of frictional type and cross-sectional shape is illustrated by the following example.
Los valores de β teóricos distintos de 5/3 se puede obtener para otras formulaciones de fricción y formas de sección transversal. Para flujo turbulento regido por la fricción de Manning, β tiene un límite superior de 5/3, y por lo general es mayor que 1. Para flujo laminar en canales amplios, β = 3; para mezclado o de transición de flujo laminar entre Manning turbulento, que está en el rango 5/3 < β < 3. Para el flujo en un canal amplio hidráulicamente descrito por la fórmula de Chezy, β = 3/2 (Sección 4.2). El cálculo de β como una función de tipo de fricción y la forma de la sección transversal se ilustra con el siguiente ejemplo.
Example 9-6.
Calculate the value of β
for a triangular channel with Manning friction.
Calcular el valor de β
para un canal triangular con fricción de Manning.
Equation 9-10 is the Manning equation.
Substituting R = A/P leads to Eq. 9-12.
Since P is a function of A, Eq. 9-12 can be written as follows:
La Ec. 9-10 es la ecuación de Manning.
Sustituyendo R = A/P lleva a la Eq. 9-12.
Desde P es una función de A, la Ec. 9-12 puede escribirse de la siguiente manera:
in which K1 is a constant containing n and Sf .
The latter have been assumed to be independent of either A or P.
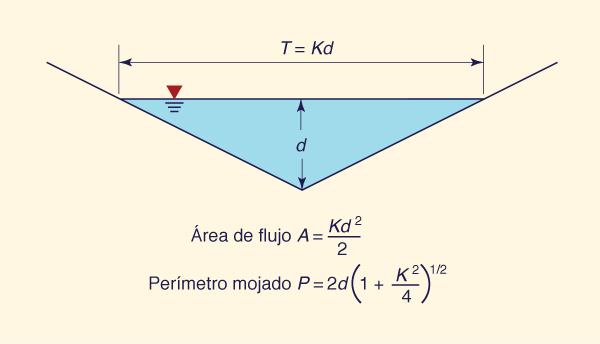
For the triangular-shaped channel of Fig. 9-9, the top width is proportional to the flow depth, say
en la que K1 es una constante que contiene n y Sf.
Estos últimos han sido asumidos para ser independiente de cualquiera de A o P.
Para el canal de forma triangular de la Fig. 9-9, el ancho de la parte superior es proporcional a la profundidad de flujo, por ejemplo
Figure 9-9 Propiedades de una sección transversal de canal triangular
and the wetted perimeter is:
y el perímetro mojado es:
Eliminating d from Eqs. 9-36 and 9-37:
Eliminando d de las Ecs. 9-36 y 9-37:
from which
del cual
in which K2 is a constant containing K.
Substituting Eq. 9-39 into Eq. 9-35 leads to:
en el que K2 es una constante que contiene K.
in which K3 is a constant containing
K1 and K2.
From Eq. 9-40:
en el que K3 es una constante
K1 y K2.
Donde la Ec. 9-40:
and the value of β for a triangular channel with Manning friction is β = 4/3.
y los valores de β para un canal triangular con fricción de Manning es
β = 4/3.
|
Las ondas cinemáticas con flujo de entrada lateral
Practical applications of stream channel routing often require the specification of lateral inflows. The latter could be either concentrated, as in the case of tributary inflow at a point along the channel reach, or distributed along the channel, as with groundwater exfiltration (for effluent streams) or infiltration (for influent streams). As with Eq. 9-9, a mass balance leads to:
Las aplicaciones prácticas del tránsito del canal de flujo a menudo requieren la especificación de los flujos de entrada laterales. Este último podría ser o bien se concentra, como en el caso de flujo de entrada tributario en un punto a lo largo del tramo del canal, o distribuidos a lo largo del canal, como con la exfiltración del agua subterránea (por corrientes de efluentes) o infiltración (para los flujos influentes). Al igual que con la Ec. 9-9, un balance de masas conduce a:
|
∂Q ∂A ____ + ____ = qL ∂x ∂t | (9-42) |
which, unlike Eq. 9-9, includes the source term qL, the lateral flow per unit channel length. For Q given in cubic meters per second and x in meters, qL is given in cubic meters per second per meter [L2 T -1].
que, a diferencia de la Ec. 9-9, incluye el término fuente qL, el flujo lateral por longitud de canal de unidad. Para Q dada en metros cúbicos por segundo y x en metros, qL es dado en metros cúbicos por segundo por metro [L2 T -1].
Multiplying Eq. 9-42 by ∂Q / ∂A (or βV), as with Eq. 9-17 (or Eq. 9-18), leads to:
|
Multiplicando la Ec. 9-42 y ∂Q / ∂A (or βV), como en la Ec. 9-17 (o Ec. 9-18), lleva a:
which is the kinematic wave equation with lateral inflow (or outflow). For qL positive, there is lateral inflow (e.g., tributary flow); for qL negative, there is lateral outflow (e.g., channel transmission losses). que es la ecuación de onda cinemática con el flujo de entrada lateral (o salida). Para qL positivo, hay flujo de entrada lateral (por ejemplo, el flujo afluente); para qL negativo, no hay flujo de salida lateral (por ejemplo, las pérdidas de transmisión del canal). Applicability of Kinematic Waves / Aplicabilidad de la onda cinemática The kinematic wave celerity is a fundamental streamflow property. Flood waves which approximate kinematic waves travel with the kinematic wave celerity (c = βV) and are subject to very little or no attenuation. La celeridad de la onda cinemática es una propiedad fundamental de caudales. Las ondas de avenida las cuales se aproximana las ondas cinemáticas viajan con la celeridad de la onda cinemática (c = βV) y están sujetos a muy poca o ninguna atenuación. In practice, flood waves are kinematic if they are of long duration (Fig. 9-10) or travel on a channel of steep slope. Criteria for the applicability of kinematic waves to overland flow [20] (Section 4.2) and stream channel flow [14] have been developed. The stream channel criterion states that in order for a wave to be kinematic, it should satisfy the following dimensionless inequality: En la práctica, las ondas de avenida son cinemáticas si son de larga duración (Fig. 9-10) o viajan en un canal de pendiente pronunciada. Los criterios para la aplicabilidad de la ondas cinemáticas para el flujo superficial [20] (Sección 4.2) y el flujo de canal de corriente [14] se han desarrollado. El criterio del canal de flujo establece que para que una onda sea cinemática, debe satisfacer la siguiente desigualdad sin dimensiones:
in which tr is the time-of-rise of the inflow hydrograph, So is the bottom slope, Vo is the average velocity, and do is the average flow depth.
For 95% accuracy in one period of translation, a value of
en la que tr es el aumento de tiempo del hidrograma del flujo de entrada,
So es la pendiente del fondo, Vo es la velocidad media, y do es la profundidad media de flujo. Para una precisión del 95% en un período de traslación, un valor de
9.3 ONDAS DIFUSIVAS
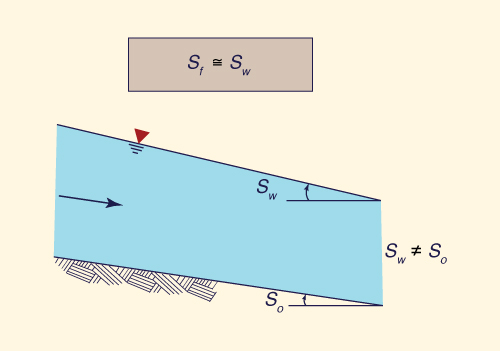
In Section 9.1, the Muskingum method was used to calculate unsteady flows in a hydrologic sense. In Section 9.2, the principle of mass conservation was coupled with a uniform flow formula to derive the kinematic wave equation. Solutions to this equation have been widely used in hydrologic practice, particularly for overland flow and other routing applications involving steep slopes or slow-rising hydrographs. En la Sección 9.1, se utilizó el método Muskingum para calcular los flujos inestables en un sentido hidrológico. En la Sección 9.2, el principio de conservación de la masa se acopló con una fórmula de flujo uniforme para derivar la ecuación de onda cinemática. Las soluciones a esta ecuación han sido ampliamente utilizados en la práctica hidrológica, en particular para el flujo superficial y otras aplicaciones de tránsito que implican fuertes pendientes o hidrogramas de lento aumento. The Muskingum method and linear kinematic wave solutions show striking similarities. Both methods have the same type of routing equation. The Muskingum method, however, can calculate hydrograph diffusion, whereas the kinematic wave can do so only by the introduction of numerical diffusion. The latter is dependent on the grid size and type of numerical scheme. El método de Muskingum y soluciones de onda cinemáticos lineales muestran similitudes sorprendentes. Ambos métodos tienen el mismo tipo de ecuación de tránsito. El método de Muskingum, sin embargo, se puede calcular la difusión del hidrograma, mientras que la onda cinemática puede hacerlo sólo por la introducción de la difusión numérica. Este último es dependiente del tamaño de la rejilla y tipo de esquema numérico. Kinematic wave theory can be enhanced by allowing a small amount of physical diffusion in its formulation [10]. In this way, an improved type of kinematic wave can be formulated, a kinematic-with-diffusion wave, for short, a diffusion wave. A definite advantage of the diffusion wave is that it includes the diffusion which is present in most natural unsteady open channel flows. Teoría de la onda cinemática se puede mejorar al permitir una pequeña cantidad de difusión física en su formulación [10]. De esta manera, un tipo mejorado de onda cinemática puede ser formulado, una onda cinemática-con-difusión, para abreviar, una onda de difusión. Una ventaja definitiva de la onda de difusión es que incluye la difusión que está presente en la mayoría de los flujos de canal abierto inestables naturales. Difusión ecuación de onda In Section 9.2, the kinematic wave equation was derived by using a statement of steady uniform flow (i.e., friction slope is equal to bottom slope) in lieu of momentum conservation. In deriving the diffusion wave, a statement of steady nonuniform flow (i.e., friction slope is equal to water surface slope) is used instead (Fig. 9-11). This leads to: En la Sección 9.2, la ecuación de onda cinemática se obtuvo mediante el uso de un principio del flujo uniforme constante (es decir, la pendiente de fricción es igual a la pendiente de abajo) en lugar de la conservación del momento. Al derivar la onda de difusión, un principio del flujo no uniforme constante (es decir, la pendiente de fricción es igual a la pendiente de la superficie del agua) es usado en su lugar (Fig. 9-11). Esto lleva a:
in which the term [So - (dy/dx)] is the water surface slope. The difference between kinematic and diffusion waves is in the term dy/dx. From a physical standpoint, the term dy/dx accounts for the natural diffusion processes present in unsteady open channel flow phenomena. en el que el término [So - (dy/dx)] es la pendiente de la superficie del agua. La diferencia entre ondas cinemáticas y de difusión se encuentra en el término dy/dx. Desde un punto de vista físico, el término dy/dx cuentas para los procesos de difusión natural presente en el fenómeno de flujo de canal abierto inestable.
To derive the diffusion wave equation, Eq. 9-45 is expressed in a slightly different form: Para derivar la ecuación de onda de difusión, la Ec. 9-45 se expresa en una forma ligeramente diferente:
in which m is the reciprocal of the square of the channel conveyance K, defined as: en la que m es el inverso del cuadrado de la conducción del canal K, que se define como:
With dA = T dy, in which T = top width, Eq. 9-46 changes to: Con dA = T dy, in which T = ancho superior, la Ec. 9-46 cambios en:
Equations 9-9 and 9-48 constitute a set of two partial differential equations describing diffusion waves. These equations can be combined into one equation with Q as dependent variable. However, it is first necessary to linearize the equations around reference flow values. For simplicity, a constant top width is assumed (i.e., a wide channel assumption). Las ecuaciones 9-9 y 9-48 constituyen un conjunto de dos ecuaciones diferenciales parciales que describen las ondas de difusión. Estas ecuaciones se pueden combinar en una ecuación con Q como variable dependiente. Sin embargo, es necesario primero para linealizar las ecuaciones alrededor de los valores del flujo de referencia. Por simplicidad, se asume una ancho superior constante (es decir, una suposición de un canal amplio). The linearization of Eqs. 9-9 and 9-48 is accomplished by small perturbation theory [4]. This procedure, while heuristic, has seemed to work well in a number of applications. The variables Q, A, and m can be expressed in terms of the sum of a reference value (with subscript o) and a small perturbation to the reference value (with superscript '): Q = Qo + Q' ; A = Ao + A' ; m = mo + m'. Substituting these into Eqs. 9-9 and 9-48, neglecting squared perturbations, and subtracting the reference flow leads to: La linealización de las Ecs. 9-9 y 9-48 se logra mediante la teoría de perturbaciones pequeñas [4]. Este procedimiento, mientras heurístico, ha parecido a funcionar bien en una serie de aplicaciones. Las variables Q, A, y m se puede expresar en términos de la suma de un valor de referencia (con subíndice o) y una pequeña perturbación al valor de referencia (con superíndice '): Q = Qo + Q' ; A = Ao + A' ; m = mo + m'. La sustitución de estos en las Ecs. 9-9 y 9-48, dejando de lado las perturbaciones al cuadrado, y restando el flujo de referencia conduce a:
y
Differentiating Eq. 9-49 with respect to x and Eq. 9-50 with respect to t gives: Diferenciando la Ec. 9-49 con respecto a x y la Ec. 9-50 con respecto a los t dados:
Using the chain rule and Eq. 9-49 yields: Utilizando la regla de la cadena y la Ec. 9-49 produce:
Combining Eq. 9-52 with Eq. 9-53: Combinando la Ec. 9-52 con la Ec. 9-53:
Combining Eqs. 9-51 and 9-54 and rearranging terms, yields: Combinando las Ecs. 9-51 y 9-54 y reordenando los términos, se obtiene:
Since by definition: mQ 2 = Sf, it follows that Dado que, por definición: mQ 2 = Sf, se deduce que
y también
Substituting Eqs. 9-56 and 9-57 into Eq. 9-55, using the chain rule, and dropping the superscripts for simplicity, the following equation is obtained: Sustituyendo las Ecs. 9-56 y 9-57 en la Ec. 9-55, utilizando la regla de la cadena, y dejando los superíndices por simplicidad, se obtiene la siguiente ecuación:
The left side of Eq. 9-58 is recognized as the kinematic wave equation, with ∂Q/∂A as the kinematic wave celerity.
The right side is a second-order (partial differential) term that accounts for the physical diffusion effect.
The coefficient of the second-order term has the units of diffusivity
El lado izquierdo de la Ec. 9-58 es reconocida como la ecuación de onda cinemática, con
∂Q/∂A como la celeridad de la onda cinemática.
El lado derecho es un término de segundo orden (en derivadas parciales) que se atribuye el efecto de difusión física. El coeficiente del término de segundo orden tiene las unidades de difusividad
The hydraulic diffusivity is a characteristic of the flow and channel, defined as: La difusividad hidráulica es una característica del flujo y el canal, que se define como:
in which qo = Qo/T is the reference flow per unit of channel width. From Eq. 9-59, it is concluded that the hydraulic diffusivity is small for steep bottom slopes (e.g., those of small mountain streams), and large for mild bottom slopes (e.g., tidal rivers). en la que qo = Qo/T es el flujo de referencia por unidad del ancho del canal. De la Ec. 9-59, se concluye que la difusividad hidráulica es pequeño para pendientes de fondo pronunciadas (por ejemplo, los pequeños ríos de montaña), y grandes para pendientes de fondo suaves (por ejemplo, ríos de marea). Equation 9-58 describes the movement of flood waves in a better way than Eq. 9-17 or 9-18. It falls short from describing the full momentum effects, but it does physically account for peak flow attenuation. La Ecuación 9-58 describe el movimiento de las ondas de inundación de una manera mejor que la Ec. 9-17 o 9-18. No llega a partir de la descripción de los efectos del momento completo, pero sí físicamente representan la atenuación de flujo máximo. Equation 9-58 is a second-order parabolic partial differential equation. It can be solved analytically, leading to Hayami's diffusion analogy solution for flood waves [7], or numerically with the aid of a numerical scheme for parabolic equations such as the Crank-Nicolson scheme [3]. An alternate approach is to match the hydraulic diffusivity with the numerical diffusion coefficient of the Muskingum scheme. This approach is the basis of the Muskingum-Cunge method [4, 12] (Section 9.4). La Ec. 9-58 es una ecuación diferencial parcial parabólica de segundo orden. Se puede solucionar analíticamente, que conduce a la solución de difusión analógica de Hayami para las ondas de inundación [7], o numéricamente con la ayuda de un esquema numérico de ecuaciones parabólicas, tales como el esquema de Crank-Nicolson [3]. Un enfoque alternativo es hacer coincidir la difusividad hidráulica con el coeficiente de difusión numérica del esquema de Muskingum. Este enfoque es la base del método de Muskingum-Cunge [4, 12] (Sección 9.4). Aplicabilidad de las ondas de difusión Most flood waves have a small amount of physical diffusion; therefore, they are better approximated by the diffusion wave rather than by the kinematic wave. For this reason, diffusion waves apply to a much wider range of practical problems than kinematic waves. Where the diffusion wave fails, only the dynamic wave can properly describe the translation and diffusion of flood waves. The dynamic wave, however, is very strongly diffusive, especially for flows well in the subcritical regime [14]. In practice, most flood flows are only mildly diffusive, and therefore, are subject to modeling with the diffusion wave. La mayoría de las ondas de avenida tienen una pequeña cantidad de difusión física; por lo tanto, están mejor aproximada por la onda de difusión en lugar de la onda cinemática. Por esta razón, las ondas de difusión se aplican a una gama mucho más amplia de los problemas prácticos que las ondas cinemáticas. Cuando la onda de difusión falla, sólo la onda dinámica se puede describir adecuadamente la traducción y difusión de las ondas de avenida. La onda dinámica, sin embargo, es muy fuertemente difusivo, especialmente para flujos de manantiales en el régimen subcrítico [14]. En la práctica, la mayoría de los flujos de inundación son sólo ligeramente por difusión, y por lo tanto, están sujetas a modelar con la onda de difusión. To determine if a wave is a diffusion wave, it should satisfy the following dimensionless inequality [14]: Para determinar si una onda es una onda de difusión, debe satisfacer la siguiente desigualdad adimensional [14]:
in which tr is the time-of-rise of the inflow hydrograph, So is the bottom slope, do is the average flow depth, and g is the gravitational acceleration. The greater the left side of this inequality, the more likely it is that the wave is a diffusion wave. In practice, a value of N = 15 is recommended for general use. en la que tr es el aumento de tiempo del hidrograma de flujo de entrada, So es la pendiente del fondo , do es la profundidad del flujo medio, y g es la aceleración de la gravedad. Cuanto mayor sea el lado izquierdo de esta desigualdad, lo más probable es que la onda es una onda de difusión. En la práctica, un valor de N = 15 se recomienda para el uso general.
9.4 EL MÉTODO MUSKINGUM-CUNGE
*****1610220115**** The Muskingum method can calculate runoff diffusion, ostensibly by varying the parameter X. A numerical solution of the linear kinematic wave equation using a third-order accurate scheme (C = 1) leads to pure flood hydrograph translation (see Example 9-3, Part 1). Other numerical solutions to the linear kinematic wave equation invariably produce a certain amount of numerical diffusion and/or dispersion (See Example 9-3, Part 2). The Muskingum and linear kinematic wave routing equations are strikingly similar. Furthermore, unlike the kinematic wave equation, the diffusion wave equation does have the capability to describe physical diffusion. El método de Muskingum puede calcular la difusión de escorrentía, aparentemente variando el parámetro X. Una solución numérica de la ecuación de onda cinemática lineal utilizando un esquema de tercer orden de exactitud (C = 1) conduce a la traslación del hidrograma de avenida puro (véase el Ejemplo 9-3, Parte 1). Otras soluciones numéricas a la ecuación de onda cinemática lineal invariablemente producen una cierta cantidad de difusión y / o dispersión numérica (Véase el Ejemplo 9-3, Parte 2). Las ecuaciones de tránsito de onda cinemática lineal y de Muskingum son sorprendentemente similares. Además, a diferencia de la ecuación de onda cinemática, la ecuación de onda de difusión tiene la capacidad para describir la difusión física. From these propositions, Cunge [4] concluded that the Muskingum method is a linear kinematic wave solution and that the flood wave attenuation shown by the calculation is due to the numerical diffusion of the scheme itself. To prove this assertion, the kinematic wave equation (Eq. 9-18) is discretized on the x-t plane (Fig. 9-12) in a way that parallels the Muskingum method, centering the spatial derivative and off-centering the temporal derivative by means of a weighting factor X: A partir de estas proposiciones, Cunge [4] concluyó que el método Muskingum es una solución onda cinemática lineal y que la atenuación de la onda de inundación se muestra por el cálculo debido a la difusión numérica del propio régimen. Para probar esta afirmación, la ecuación de onda cinemática (Ec. 9 a 18) está discretizada en el x-t plano (Fig. 9-12) de una manera que es paralelo a el método Muskingum, el centrado de la derivada espacial y fuera del centro de la derivada temporal por medio de un factor de ponderación X :
in which c = βV is the kinematic wave celerity. en la que c = βV es la celeridad de la onda cinemática.
Solving Eq. 9-61 for the unknown discharge leads to the following routing equation: La solución de la ecuación. 9-61 para la descarga desconocida conduce a la siguiente ecuación de tránsito:
The routing coefficients are: Los coeficientes de tránsito son:
By defining the travel time Al definir el tiempo de viaje
it is seen that the two sets of Eqs. 9-63 to 9-65 and Eqs. 9-4 to 9-6 are the same. se ve que los dos conjuntos de Ecs. 9-63 a 9-65 y las Ecs. 9-4 a 9-6 son los mismos. Equation 9-66 confirms that K is in fact the flood wave travel time, i.e., the time it takes a given discharge to travel the reach length Δx with the kinematic wave celerity c. In a linear mode, c is constant and equal to a reference value; in a nonlinear mode, it varies with discharge. La Ec. 9-66 confirma que K es, de hecho, el tiempo de viaje onda de inundación, es decir, el tiempo que tarda una descarga dada en recorrer la longitud del tramo Δx con la celeridad de onda cinemática c. En un modo lineal, c es constante e igual a un valor de referencia; en un modo no lineal, que varía con la descarga.
It can be seen that for X = 0.5, Eqs. 9-63 to 9-65 reduce to the routing coefficients of the linear second-order-accurate kinematic wave solution, Eqs. 9-22 to 9-24.
For X = 0.5 and C = 1 (C =
Se puede observar que para X = 0.5, las Ecs. 9-63 a 9-65 se reducen a los coeficientes de
tránsito de la solución de onda cinemática de segundo orden con precisión lineal, las Ecs. 9-22 a 9-24.
Para X = 0.5 y C = C = 1 (C =
In practice, the numerical diffusion can be used to simulate the physical diffusion of the actual flood wave. By expanding the discrete function Q (jΔx, n Δt) in Taylor series about grid point (jΔx, n Δt), the numerical diffusion coefficient of the Muskingum scheme is derived (see Appendix B): En la práctica, la difusión numérica se puede utilizar para simular la difusión física de la onda de avenida actual. Con la ampliación de la función discreta Q (jΔx, n Δt) en la serie de Taylor alrededor del punto de rejilla (jΔx, n Δt), el coeficiente de difusión numérica del esquema se deriva (ver Apéndice B):
in which νn is the numerical diffusion coefficient of the Muskingum scheme. This equation reveals the following: en la que νn es el coeficiente de difusión numérica del esquema de Muskingum. Esta ecuación revela lo siguiente:
A predictive equation for X can be obtained by matching the hydraulic diffusivity νh (Eq. 9-59) with the numerical diffusion coefficient of the Muskingum scheme νn (Eq. 9-67). This leads to the following expression for X: Una ecuación de predicción para X se pueden obtener haciendo coincidir la difusividad hidráulica νh (Ec. 9-59) con el coeficiente de difusión numérica de el esquema de Muskingum νn (Ec. 9-67). Esto conduce a la siguiente expresión para X:
With X calculated by Eq. 9-68, the Muskingum method is referred to as Muskingum-Cunge method [12]. Using Eq. 9-68, the routing parameter X can be calculated as a function of the following numerical and physical properties: Con X calculada por la Ec. 9-68, el método de Muskingum se conoce como método de Muskingum-Cunge [12]. Utilizando la Ec. 9-68, el parámetro de enrutamiento X se puede calcular en función de las siguientes propiedades numéricas y físicas:
It should be noted that Eq. 9-68 was derived by matching physical and numerical diffusion (i.e., second-order processes), and does not account for dispersion (a third-order process). Therefore, in order to simulate wave diffusion properly with the Muskingum-Cunge method, it is necessary to optimize numerical diffusion (with Eq. 9-68) while minimizing numerical dispersion by keeping the value of C as close to 1 as practicable. Debe observarse que la Ec. 9-68 se derivó mediante la búsqueda de la difusión física y numérica (es decir, procesos, de segundo orden), y no tiene en cuenta la dispersión (un proceso de tercer orden). Por lo tanto, con el fin de simular la difusión de onda correctamente con el método de Muskingum-Cunge, es necesario optimizar la difusión numérica (con la Ec. 9-68) y reducir al mínimo la dispersión numérica manteniendo el valor de C lo más cercano a 1 como sea posible.
A unique feature of the Muskingum-Cunge method is the grid independence of the calculated outflow hydrograph, which sets it apart from other linear kinematic wave solutions featuring uncontrolled numerical diffusion and dispersion (e.g., the convex method).
If numerical dispersion is minimized, the calculated outflow at the downstream end of a channel reach will be essentially the same, regardless of how many subreaches are used in the computation.
This is because X is a function of Δx,
and the routing coefficients C0, C1,
and
Una característica única del método de Muskingum-Cunge es la independencia de la rejilla
del hidrograma del flujo de salida calculada, lo que lo diferencia de otras soluciones de onda cinemáticos lineales que ofrecen la difusión y dispersión numérica incontrolada (por ejemplo, el método convexo). Si se reduce al mínimo la dispersión numérica, la salida de flujo calculada en el extremo
aguas abajo del tramo del canal será esencialmente la misma, independientemente del número de subtramos utilizados en el cálculo.
Esto se debe a X es una función de Δx,
y los coeficientes de tránsito C0, C1,
y An improved version of the Muskingum-Cunge method is due to Ponce and Yevjevich [15]. The C value is the Courant number, i.e. , the ratio of wave celerity c to grid celerity Δx/ Δt: Una versión mejorada del método de Muskingum-Cunge se debe a Ponce y Yevjevich [15]. El C valor es el número de Courant, es decir, la relación entre la celeridad de la onda c a la celeridad de la rejilla Δx/ Δt:
The grid diffusivity is defined as the numerical diffusivity for the case of X = 0. From Eq. 9-67, the grid diffusivity is: La difusividad de la rejilla se define como la difusividad numérica para el caso de X = 0. De la Ec. 9-67, la difusividad de rejilla es:
The cell Reynolds number [18] is defined as the ratio of hydraulic diffusivity (Eq. 9-59) to grid diffusivity (Eq. 9-70). This leads to: La célula del número de Reynolds [18] se define como la relación de la difusividad hidráulica (Ec. 9 a 59) para la difusividad de rejilla (Ec. 9 a 70). Esto lleva a:
in which D = cell Reynolds number. Therefore: en la que D = célula del número de Reynolds. Por lo tanto
Equations 9-71 and 9-72 imply that for very small values of Δx, D may be greater than 1, leading to negative values of X. In fact, for the characteristic reach length Las Ecuaciones 9-71 y 9-72 implican que, para valores muy pequeños de Δx, D puede ser mayor que 1, lo que lleva a los valores negativos de X. De hecho, para la longitud del tramo característico
the cell Reynolds number is D = 1, and X = 0. Therefore, in the Muskingum-Cunge method, reach lengths shorter than the characteristic reach length result in negative values of X. This should be contrasted with the classical Muskingum method (Section 9.1), in which X is restricted in the range 0.0 ≤ X ≤ 0.5. In the classical Muskingum, X is interpreted as a weighting factor. As shown by Eqs. 9-71 and 9-72, nonnegative values of X are associated with long reaches, typical of the manual computation used in the development and early application of the Muskingum method. La célula del número de Reynolds es D = 1, y X = 0. Por lo tanto, en el método Muskingum-Cunge, alcanzar longitudes más cortas que la longitud del tramo característico resulta en valores negativos de X. Esto debe ser contrastado con el método de Muskingum clásico (Sección 9.1), en la que X está restringido en el rango de 0.0 ≤ X ≤ 0.5. En el Muskingum clásico, X se interpreta como un factor de ponderación. Como se muestra por las Ecs. 9-71 y 9-72, los valores no negativos de X se asocian con tramos largos, típicos del cálculo manual utilizado en el desarrollo y la aplicación anticipada del método de Muskingum. In the Muskingum-Cunge method, however, X is interpreted in a moment-matching sense [2] or diffusion-matching factor. Therefore, negative values of X are entirely possible. This feature allows the use of shorter reaches than would otherwise be possible if X were restricted to nonnegative values. En el método de Muskingum-Cunge, sin embargo, X es interpretado en un sentido de momento de coincidencia [2] o factor de difusión de coincidencia. Por lo tanto, los valores negativos de X son totalmente posibles. Esta característica permite el uso de tramos más cortos de lo que sería posible si X estaban restringidas a valores no negativos. The substitution of Eqs. 9-69 and 9-72 into Eqs. 9-63 to 9-65 leads to routing coefficients expressed in terms of Courant and cell Reynolds numbers: La sustitución de las Ecs. 9-69 y 9-72 en las Ecs. 9-63 a 9-65 conduce a encaminar coeficientes expresados en términos de números de Courant y célula de Reynolds:
The calculation of routing parameters C and D, Eqs. 9-69 and 9-71, can be performed in several ways. The wave celerity can be calculated with either Eq. 9-16 or Eq. 9-34. With Eq. 9-16, c = βV; with Eq. 9-34, c = (1/T) dQ/dy. Theoretically, these two equations are the same. For practical applications, if a stage-discharge rating and cross-sectional geometry are available (i.e., stage-discharge-top width tables), Eq. 9-34 is preferred over Eq. 9-16 because it accounts directly for cross-sectional shape. In the absence of a stage-discharge rating and cross-sectional data, Eq. 9-16 can be used to estimate flood wave celerity. El cálculo de los parámetros de tránsito C y D, Ecs. 9-69 y 9-71, se puede realizar de varias maneras. La celeridad de la onda se puede calcular con la ecuación ya sea 9-16 o Eq. 9-34. Con la Ec. 9-16, c = β V; con la Ec. 9-34, c = (1/T) dQ/dy. Teóricamente, estas dos ecuaciones son los mismas. Para aplicaciones prácticas, si una calificación de nivel-caudal y la geometría de la sección transversal están disponibles (es decir, tablas amplias de nivel de descarga superior), la Ec. 9-34 se prefiere sobre la Ec. 9-16 porque da cuenta directamente para la forma en sección transversal. En ausencia de una calificación de nivel-caudal y los datos de la sección transversal, la Ec. 9-16 se puede utilizar para estimar la celeridad de onda de inundación. With the aid of Eqs. 9-69 and 9-71, the routing parameters may be based on flow characteristics. The calculations can proceed in a linear or nonlinear mode. In the linear mode, the routing parameters are based on reference flow values and kept constant throughout the computation in time. The choice of reference flow has a bearing on the calculated results [2, 15], although the overall effect is likely to be small. For practical applications, either an average or peak flow value can be used as reference flow. The peak flow value has the advantage that it can be readily ascertained, although a better approximation may be obtained by using an average value [15]. The linear mode of computation is referred to as the constant-parameter Muskingum-Cunge method to distinguish it from the variable-parameter Muskingum-Cunge method, in which the routing parameters are allowed to vary with the flow. The constant parameter method resembles the Muskingum method, with the difference that the routing parameters are based on measurable flow and channel characteristics instead of historical streamflow data. Con la ayuda de las Ecs. 9-69 y 9-71, los parámetros de tránsito puede basarse en las características del flujo. Los cálculos pueden proceder de un modo lineal o no lineal. En el modo lineal, los parámetros de tránsito se basan en valores de flujo de referencia y se mantienen constantes durante todo el cálculo en el tiempo. La elección del flujo de referencia tiene una incidencia en los resultados calculados [2, 15], aunque es probable que sea pequeño el efecto global. Para aplicaciones prácticos, ya sea un promedio o valor de flujo máximo se pueden utilizar como flujo de referencia. El valor de flujo máximo tiene la ventaja de que se puede determinar fácilmente, a pesar de una mejor aproximación puede ser obtenida mediante el uso de un valor medio [15]. El modo lineal del cálculo se conoce como la constante del parámetro del método de Muskingum-Cunge para distinguirla de la variable-parámetro del método de Muskingum-Cunge, en el que se permite que los parámetros de tránsito para variar con el flujo. El método de parámetro constante asemeja al método Muskingum, con la diferencia de que los parámetros de tránsito se basan en las características de flujo medibles y del canal en lugar de datos de caudal históricos.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Requisitos de resolución
When using the Muskingum-Cunge method, care should be taken to ensure that the values of Δx and Δt are sufficiently small to approximate closely the actual shape of the hydrograph. For smoothly rising hydrographs, a minimum value of tp /Δt = 5 is recommended. This requirement usually results in the hydrograph time base being resolved into at least 15 to 25 discrete points, considered adequate for Muskingum routing.
Cuando se utiliza el método de Muskingum-Cunge, se debe tener cuidado para asegurar que los valores de Δx y Δ t son lo suficientemente pequeñas para aproximarse estrechamente a la forma real del hidrograma. Para hidrogramas crecientes suaves, un valor mínimo de tp /Δt = 5 se recomienda. Este requisito generalmente resulta en la base de tiempo del hidrograma que se resuelve en al menos 15 a 25 puntos discretos, considerada adecuada para el tránsito de Muskingum.
Unlike temporal resolution, there is no definite criteria for spatial resolution. A criterion borne out by experience is based on the fact that Courant and cell Reynolds numbers are inversely related to reach length Δx. Therefore, to keep Δx sufficiently small, Courant and cell Reynolds numbers should be kept sufficiently large. This leads to the practical criterion [16]:
A diferencia de resolución temporal, no hay criterios definidos para la resolución espacial. Un criterio confirmado por la experiencia se basa en el hecho de que el número de Courant y la célula de Reynolds son inversamente proporcionales a la longitud del tramo Δx. Por lo tanto, para mantener Δx lo suficientemente pequeña, los números de Courant y célula de Reynolds deben mantenerse lo suficientemente grande. Esto conduce al criterio práctico [16]:
| C + D ≥ 1 | (9-77) |
which can be written as follows: -1 + C + D ≥ 0. This confirms the necessity of avoiding negative values of C0 in Muskingum-Cunge routing (see Eq. 9-74). Experience has shown that negative values of either C1 or C2 do not adversely affect the method's overall accuracy [16].
que se puede escribir de la siguiente manera: -1 + C + D ≥ 0. Esto confirma la necesidad de evitar valores negativos de C0 en tránsito de Muskingum-Cunge (véase Ec. 9-74). La experiencia ha demostrado que los valores negativos de ambos C1 o C2 no afectan negativamente a la precisión global del método [16].
Notwithstanding Eq. 9-77, the Muskingum-Cunge method works best when the numerical dispersion is minimized, that is, when C ≅ 1. Values of C substantially less than 1 are likely to cause the notorious dips, or negative outflows, in portions of the calculated hydrograph. This computational anomaly is attributed to excessive numerical dispersion and should be avoided.
A pesar de la Ec. 9-77, el método Muskingum-Cunge funciona mejor cuando se minimiza la dispersión numérica, es decir, cuando C ≅ 1. Los valores de C sustancialmente menor que 1 es probable que causen los huecos notorios, o salidas negativas, en porciones del hidrograma calculado. Esta anomalía computacional se atribuye a la dispersión numérica excesiva y debe ser evitado.
Método de Muskingum-Cunge Método No Lineal
The kinematic wave equation, Eq. 9-18, is nonlinear because the kinematic wave celerity varies with discharge. The nonlinearity is mild, among other things because the wave celerity variation is usually restricted within a narrow range. However, in certain cases it may be necessary to account for this nonlinearity. This can be done in two ways: (1) during the discretization, by allowing the wave celerity to vary, resulting in a nonlinear numerical scheme to be solved by iterative means; and (2) after the discretization, by varying the routing parameters, as in the variable-parameter Muskingum-Cunge method [15]. The latter approach is particularly useful if the overall nonlinear effect is small, which is often the case.
La ecuación de onda cinemática, la Ec. 9-18, es no lineal debido a la celeridad de la onda cinemática varía con la descarga. La no linealidad es leve, entre otras cosas porque la variación celeridad de la onda se restringe generalmente dentro de un rango estrecho. Sin embargo, en ciertos casos puede ser necesario para dar cuenta de esta no linealidad. Esto se puede hacer de dos maneras: (1) durante la discretización, al permitir que la celeridad de la onda varíe, lo que resulta en un esquema numérico no lineal para ser resueltos por medio de iteraciones; y (2) después de la discretización, mediante la variación de los parámetros de tránsito, como en la variable-parámetro del método de Muskingum-Cunge [15]. El último enfoque es particularmente útil si el efecto no lineal general es pequeño, lo que es a menudo el caso.
In the variable parameter method, the routing parameters are allowed to vary with the flow. The values of C and D are based on local qo and c values instead of peak flow or other reference value as in the constant-parameter method. To vary the routing parameters, the most expedient way is to obtain an average value of qo and c for each computational cell. This can be achieved with a direct three-point average of the values at the known grid points (see Fig. 9-11), or by an iterative four-point average, which includes the unknown grid point. To improve the convergence of the iterative four-point procedure, the three-point average can be used as the first guess of the iteration. Once qo and c have been determined for each computational cell, the Courant and cell Reynolds numbers are calculated by Eqs. 9-69 and 9-71. The value of bottom slope So remains unchanged within each computational cell.
En el método de parámetro variable, los parámetros de trásnito se les permite variar con el flujo. Los valores de C y D se basan en valores qo and c locales en lugar de flujo máximo o valor de referencia como en el método constante parámetro. Para variar los parámetros de ruta, la forma más adecuada es obtener un valor medio de qo y c para cada celda computacional. Esto se puede lograr con un promedio de tres puntos directos de los valores en los puntos de rejilla conocidos (véase Fig. 9-11), o en un promedio de cuatro puntos iterativos, que incluye el punto de la cuadrícula desconocido. Para mejorar la convergencia del procedimiento iterativo de cuatro puntos, la media de tres puntos se puede utilizar como la primera suposición de la iteración. Una vez q o y c se hayan determinado para cada celda computacional, los números de Courant y la celda de Reynolds son calculados por las Ecs. 9-69 y 9-71. El valor de la pendiente del fondo So se mantiene sin cambios dentro de cada celda computacional.
******1610311330*******
The variable parameter Muskingum-Cunge method represents a small yet sometimes perceptible improvement over the constant parameter method. The differences are likely to be more marked for very long reaches and/or wide variations in flow levels. Flood hydrographs calculated with variable parameters show a certain amount of distortion, either wave steepening in the case of flows contained inbank or wave attenuation (flattening) in the case of typical overbank flows. This is a physical manifestation of the nonlinear effect, i.e., different flow levels traveling with different celerities. On the other hand, flood hydrographs calculated using constant parameters do not show wave distortion.
El parámetro variable del método de Muskingum-Cunge representa una mejora pequeña pero a veces se detectan en el método del parámetro constante. Las diferencias son probablemente más marcado para tramos muy largos y / o grandes variaciones en los niveles de flujo. Los hidrogramas de avenida calculados con parámetros variables muestran una cierta cantidad de distorsión, ya sea empinamiento de la onda en el caso de los flujos contenidos dentro del banco o atenuación de la onda (aplanamiento) en el caso de los flujos típicos de desbordamiento. Esta es una manifestación física del efecto no lineal, es decir, los diferentes niveles de flujo que viajan con diferentes celeridades. Por otro lado, hidrogramas de avenida calculados usando parámetros constantes no muestran distorsión de la onda.
Evaluación de Muskingum-Cunge Método
The Muskingum-Cunge method is a physically based alternative to the Muskingum method. Unlike the Muskingum method where the parameters are calibrated using streamflow data, in the Muskingum-Cunge method the parameters are calculated based on flow and channel characteristics. This makes possible channel routing without the need for time-consuming and cumbersome parameter calibration. More importantly, it makes possible extensive channel routing in ungaged streams with a reasonable expectation of accuracy. With the variable-parameter feature, nonlinear properties of flood waves (which could otherwise only be obtained by more elaborate numerical procedures) can be described within the context of the Muskingum formulation.
El método de Muskingum-Cunge es una alternativa de base física para el método de Muskingum. A diferencia del método de Muskingum, donde los parámetros son calibrados utilizando datos de caudal, en el método de Muskingum-Cunge los parámetros se calculan en base a las características de flujo y de canal. Esto hace posible el tránsito de avenidas sin necesidad de mucho tiempo y la calibración del parámetro complicado. Más importante aún, hace posible el tránsito del canal extenso en corrientes no aforadas con una expectativa razonable de precisión. Con la característica de parámetro variable, de propiedades no lineales de las ondas de avenida (que de otro modo sólo podría obtenerse por más procedimientos numéricos elaborados) pueden ser descritas en el contexto de la formulación de Muskingum.
Like the Muskingum method, the Muskingum-Cunge method is limited to diffusion waves. Furthermore, the Muskingum-Cunge method is based on a single-valued rating and does not take into account strong flow non-uniformity or unsteady flows exhibiting substantial loops in discharge-stage rating (i.e., dynamic waves). Thus, the Muskingum-Cunge method is suited for channel routing in natural streams without significant backwater effects and for unsteady flows that classify under the diffusion wave criterion (Eq. 9-60).
Al igual que el método de Muskingum, el método de Muskingum-Cunge se limita a las ondas de difusión. Por otra parte, el método de Muskingum-Cunge se basa en una clasificación de valor único y no toma en cuenta un flujo fuerte no uniforme o flujos inestables que presentan bucles sustanciales en la clasificación del nivel de descarga (es decir, las ondas dinámicas). Por lo tanto, el método de Muskingum-Cunge es adecuado para el tránsito de canales en cauces naturales sin efectos significativos de remanso y de flujos inestables que clasifican bajo el criterio de la onda de difusión (Ec. 9-60).
An important difference between the Muskingum and Muskingum-Cunge methods should be noted. The Muskingum method is based on the storage concept (Chapter 4) and, therefore, it is lumped, with the parameters K and X being reach averages. The Muskingum-Cunge method, however, is distributed in nature, with the parameters C and D being based on values evaluated at channel cross sections. Therefore, for the Muskingum-Cunge method to improve on the Muskingum method, it is necessary that the routing parameters evaluated at channel cross sections be representative of the channel reach under consideration.
Una diferencia importante entre los métodos de Muskingum y de Muskingum-Cunge debe tenerse en cuenta. El método Muskingum se basa en el concepto de almacenamiento (Capítulo 4) y, por lo tanto, se agrupa, con los parámetros K y X son promedios de tramos. El método Muskingum-Cunge, sin embargo, se distribuye en la naturaleza, con los parámetros C y D se basa en los valores evaluados a secciones transversales de canal. Por lo tanto, para el método de Muskingum-Cunge para mejorar el método de Muskingum, es necesario que los parámetros de tránsito evaluados en secciones transversales de canal sean representativos del tramo del canal bajo consideración.
Historically, the Muskingum method has been calibrated using streamflow data. On the contrary, the Muskingum-Cunge method relies on physical characteristics such as rating curves, cross-sectional data and channel slope. The different data requirements reflect the different theoretical bases of the methods, i.e., lumped storage concept in the Muskingum method, and distributed kinematic/diffusion wave theory in the Muskingum-Cunge method.
Históricamente, el método de Muskingum ha sido calibrado usando datos de caudal. Por el contrario, el método de Muskingum-Cunge se basa en las características físicas, tales como curvas de gasto, datos de sección transversal y pendiente del canal. Los requisitos de datos diferentes reflejan las diferentes bases teóricas de los métodos, es decir, el concepto de almacenamiento agrupado en el método de Muskingum, y la teoría de la onda cinemática / difusión distribuida en el método de Muskingum-Cunge.
9.5 INTRODUCCIÓN A LAS ONDAS DINÁMICAS
|
|
In Section 9.2, kinematic waves were formulated by simplifying the momentum conservation principle to a statement of steady uniform flow. In Section 9.3, diffusion waves were formulated by simplifying the momentum principle to a statement of steady nonuniform flow. These two waves, in particular the diffusion wave, have been extensively used in stream channel routing applications. The Muskingum and Muskingum-Cunge methods are examples of calculations using the concept of diffusion wave.
En la Sección 9.2, las ondas cinemáticas se formularon mediante la simplificación del principio de conservación del momento a un principio de flujo constante uniforme. En la Sección 9.3, las ondas de difusión se formularon mediante la simplificación del principio de momento a un principio de flujo no uniforme constante. Estas dos ondas, en particular, la onda de difusión, se han utilizado ampliamente en aplicaciones de tránsito de canal de corriente. Los métodos de Muskingum y de Muskingum-Cunge son ejemplos de cálculos utilizando el concepto de onda de difusión.
A third type of open channel flow wave, the dynamic wave, is formulated by taking into account the complete momentum principle, including its inertial components. As such, the dynamic wave contains more physical information than either kinematic or diffusion waves. Dynamic wave solutions, however, are more complicated than either kinematic or diffusion wave solutions.
Un tercer tipo de onda de flujo en canales abiertos, la onda dinámica, se formula teniendo en cuenta el principio de momento completa, incluyendo sus componentes inerciales. Como tal, la onda dinámica contiene más información física que cualquiera de ondas cinemáticas o de difusión. Las soluciones de onda dinámicas, sin embargo, son más complicados que cualquiera de las soluciones de onda cinemática o de difusión.
In a dynamic wave solution, the equations of mass and momentum conservation are solved by a numerical procedure, either the method of finite differences, the method of characteristics, or the finite element method. In the method of finite differences, the partial differential equations are discretized following a chosen numerical scheme [9]. The method of characteristics is based on the conversion of the set of partial differential equations into a related set of ordinary differential equations, and the solution along a characteristic grid, i.e. a grid that follows characteristic directions (Fig. 4-16). The method of finite elements solves a set of integral equations over a chosen grid of finite elements.
En una solución de la onda dinámica, las ecuaciones de la masa y conservación del momento se resuelven mediante un procedimiento numérico, ya sea el método de las diferencias finitas, el método de características, o el método de elementos finitos. En el método de las diferencias finitas, las ecuaciones diferenciales parciales se discretizan siguiendo un esquema numérico seleccionado [9]. El método de las características se basa en la conversión del conjunto de ecuaciones diferenciales parciales en un conjunto relacionado de ecuaciones diferenciales ordinarias, y la solución a lo largo de una cuadrícula característica, es decir, una cuadrícula que sigue instrucciones características (Fig. 4-16). El método de los elementos finitos resuelve un sistema de ecuaciones integrales más de una cuadrícula elegida de elementos finitos.
In the past four decades, the method of finite differences has come to be regarded as the most expedient way of obtaining a dynamic wave solution for practical applications [6, 9]. Among several numerical schemes that have been used in connection with the dynamic wave, the Preissmann scheme is perhaps the most popular. This is a four-point scheme, centered in the temporal derivatives and slightly off-centered in the spatial derivatives. The off-centering in the spatial derivatives introduces a small amount of numerical diffusion necessary to control the numerical stability of the nonlinear scheme. This produces a workable yet sufficiently accurate scheme.
En las últimas cuatro décadas, el método de diferencias finitas ha llegado a ser considerada como la forma más conveniente de obtener una solución de onda dinámica para aplicaciones prácticas [6, 9]. Entre los diversos esquemas numéricos que se han utilizado en relación con la onda dinámica, el esquema Preissmann es quizás la más popular. Este es un esquema de cuatro puntos, centrado en las derivadas temporales y ligeramente descentrada en las derivadas espaciales. El off-centrado en las derivadas espaciales introduce una pequeña cantidad de difusión numérica necesaria para controlar la estabilidad numérica del régimen no lineal. Esto produce un esquema viable aún suficientemente preciso.
The stream channel is divided into several reaches for computational purposes (Fig. 9-12). The application of the Preissmann scheme to the governing equations for the various reaches results in a matrix solution requiring a double sweep algorithm, i.e., one that accounts only for the nonzero entries of the coefficient matrix, which are located within a narrow band surrounding the main diagonal. This technique leads to a considerable savings in storage and execution time. With the appropriate upstream and downstream boundary conditions (Fig. 9-13), the solution of the set of hyperbolic equations marches in time until a specified number of time intervals is completed.
El canal de corriente se divide en varios tramos para fines de cálculo (Fig. 9-12). La aplicación del esquema de Preissmann a las ecuaciones que rigen para los resultados de tramos diversos en una solución de matriz que requiere un algoritmo de barrido doble, es decir, uno que representa solamente para los elementos no nulos de la matriz de coeficientes, que se encuentran dentro de una banda estrecha que rodea la diagonal principal. Esta técnica conduce un considerable ahorro en el tiempo de almacenamiento y ejecución. Con las condiciones adecuadas aguas arriba y aguas abajo (Fig. 9-13), la solución del sistema de ecuaciones hiperbólicas marcha en el tiempo hasta un número determinado de intervalos de tiempo completado.
Figure 9-13 Reach subdivision for dynamic wave routing. / Subdivisión de tramos para el tránsito de onda dinámica. |
In practice, a dynamic wave solution represents an order-of-magnitude increase in complexity and associated data requirements when compared to either kinematic or diffusion wave solutions. Its use is recommended in situations where neither kinematic nor diffusion wave solutions are likely to represent adequately the physical phenomena. In particular, dynamic wave solutions are applicable to flow over very flat slopes, flow into large reservoirs, strong backwater conditions and flow reversals. In general, the dynamic wave is recommended for cases warranting a precise determination of the unsteady variation of river stages.
En la práctica, una solución onda dinámica representa un aumento de un orden de magnitud en la complejidad y requerimientos de datos asociados en comparación con cualquiera de las soluciones de onda cinemática o de difusión. Se recomienda su uso en situaciones donde ni soluciones de onda cinemática ni de difusión es probable que represente adecuadamente los fenómenos físicos. En particular, las soluciones de onda dinámicas son aplicables a fluir sobre pendientes muy planas, desembocan en grandes reservorios, las condiciones de remanso fuertes e inversiones de flujo. En general, se recomienda la onda dinámica para los casos que ameriten la determinación precisa de la variación inestable de los niveles del río.
La relevancia de las ondas dinámicas para Ingeniería Hidrológica
Dynamic wave solutions are often referred to as hydraulic river routing. As such, they have the capability to calculate unsteady discharges and stages when presented with the appropriate geometric channel data and initial and boundary conditions. Their relevance to engineering hydrology is examined here by comparing them to kinematic and diffusion wave solutions.
Las soluciones de onda dinámicas se refieren a menudo como tránsito de río hidráulico. Como tales, tienen la capacidad para calcular las descargas inestables y niveles cuando se presenta con los datos del canal geométrico apropiado y las condiciones iniciales y de contorno. Su relevancia para la hidrología de ingeniería se examina aquí, comparándolos con las soluciones de onda cinemática y de difusión.
Kinematic waves calculate unsteady discharges; the corresponding stages are subsequently obtained from the appropriate rating curves. Usually, equilibrium (steady, uniform) rating curves are used for this purpose. Diffusion waves may or may not use equilibrium rating curves to calculate stages. Some methods, e.g., Muskingum-Cunge, use equilibrium ratings, but more elaborate diffusion wave solutions may not.
Las ondas cinemáticas calculan las descargas inestables; las etapas correspondientes se obtienen posteriormente apartir de las curvas de velocidad apropiados. Por lo general, de equilibrio (constante y uniforme) las curvas de velocidad se utilizan para este propósito. Las ondas de difusión pueden o no pueden utilizar las curvas de velocidad de equilibrio para calcular los niveles. Algunos métodos, por ejemplo, de Muskingum-Cunge, utilizar las velocidades de equilibrio, pero las soluciones de onda de difusión más elaboradas no pueden.
Dynamic waves rely on the physics of the phenomena as built into the governing equations to generate their own unsteady rating. A looped rating curve is produced at every cross section, as shown in Fig. 91-4. For any given stage, the discharge is higher in the rising limb of the hydrograph and lower in the receding limb. This loop is due to hydrodynamic reasons and should not be confused with other loops, which may be due to erosion, sedimentation, or changes in bed configuration (Chapter 15).
Las ondas dinámicas se basan en la física de los fenómenos como integrado en las ecuaciones que rigen para generar su propia velocidad inestable. Una curva de velocidad de bucle se produce en cada sección transversal, como se muestra en la Fig. 9-14. Para un nivel determinado, la descarga es mayor en la rama ascendente del hidrograma e inferior en el miembro del retroceso. Este bucle se debe a motivos hidrodinámicos y no debe ser confundido con otros bucles, que puede ser debido a la erosión, la sedimentación, o cambios en la configuración del lecho (Capítulo 15).
Figure 9-14 Sketch of the looped rating of dynamic waves./Esquema del gasto del bucle de ondas dinámicas. |
The width of the loop is a measure of the flow unsteadiness, with wider loops corresponding to highly unsteady flow, i.e., dynamic wave flow. If the loop is narrow, it implies that the flow is mildly unsteady, perhaps a diffusion wave. If the loop is practically nonexistent, the flow can be approximated as kinematic flow. In fact, the basic assumption of kinematic flow is that momentum can be simulated as steady uniform flow, i.e., that the rating curve is single-valued.
La amplitud del bucle es una medida de la inestabilidad del flujo, con bucles más amplios que corresponde al flujo altamente inestable, es decir, el flujo de la onda dinámica. Si el bucle es estrecho, que implica que el flujo es ligeramente inestable, tal vez una onda de difusión. Si el bucle es prácticamente inexistente, el flujo se puede aproximar como flujo cinemático. De hecho, el supuesto básico de flujo cinemático es que el momento se puede simular como un flujo uniforme constante, es decir, que la curva de gastos es de un solo valor.
The preceding observations lead to the conclusion that the relevance of dynamic waves in engineering hydrology is directly related to the flow unsteadiness and the associated loop in the rating curve. For highly unsteady flows such as dam-break flood waves, it may well be the only way to properly account for the looped rating. For other less unsteady flows, kinematic and diffusion waves are a viable alternative, provided their applicability can be clearly demonstrated (Eqs. 9-44 and 9-60).
Las observaciones anteriores llevan a la conclusión de que la relevancia de las ondas dinámicas en la ingeniería de hidrología está directamente relacionada con la inestabilidad de flujo y el bucle asociado en la curva de gastos. Para flujos altamente inestables, como las ondas de avenida de rotura de presa, es muy posible ser la única manera de explicar correctamente el gasto del bucle. Para otros flujos menos inestables, las ondas cinemáticas y de difusión son una alternativa viable, siempre que su aplicación pueda demostrarse claramente (Ecs. 9-44 y 9-60).
Solución de Onda de Difusión con Componente Dinámico
A simplified approach to dynamic wave routing is that of the diffusion wave with dynamic component [2]. In this approach, the complete governing equations, including inertia terms, are linearized in a similar way as with diffusion waves. This leads to a diffusion equation similar to Eq. 9-58, but with a modified hydraulic diffusivity. The equation is [5]:
Un enfoque simplificado para el tránsito de onda dinámica es la de la onda de difusión con componente dinámico [2]. En este enfoque, las ecuaciones que rigen completos, incluyendo los términos de inercia, están linealizadas de una manera similar como con las ondas de difusión. Esto conduce a una ecuación de difusión similar a la Ec. 9-58, pero con una difusividad hidráulica modificada. La ecuación es [5]:
|
∂Q ∂Q ∂Q Qo ∂2Q ______ + ( ______ ) ______ = { ( ________ ) [ 1 - (β - 1)2 Fo2 ] } _______ ∂t ∂A ∂x 2 T So ∂x2 | (9-78) |
in which the hydraulic diffusivity (i.e., the coefficient of the second-order term) is also a function of the rating curve parameter β and the Froude number, defined as:
en el que la difusividad hidráulica (es decir, el coeficiente del término de segundo orden) también es una función del parámetro de la curva de gasto β y el número de Froude, definida como:
|
Vo Fo = ___________ (g do)1/2 | (9-79) |
with g = gravitational acceleration, and do = reference flow depth.
con g = aceleración de la gravedad, y do = referencia de profundidad de flujo.
Equation 9-78 can be expressed in terms of the Vedernikov number [17]:
La Ecuación 9-78 se puede expresar en términos del número Vedernikov [17]:
|
V = (β - 1) Fo
| (9-80) |
With Eq. 9-80, Eq. 9-78 reduces to:
Con la Ec. 9-80, la Ec. 9-78 se reduce a:
|
∂Q ∂Q ∂Q Qo ∂2Q ______ + ( ______ ) ______ = [ ( ________ ) ( 1 - V 2 ) ] _______ ∂t ∂A ∂x 2 T So ∂x2 | (9-81) |
Equations 9-78 and 9-81 provide an enhanced predictive capability for the simulation of diffusion waves including a dynamic component. For instance, for β = 1.5 (i.e., Chezy friction in wide channels) and Fo = 2, the Vedernikov number V = 1 (Eq. 9-80), and the hydraulic diffusivity vanishes, which is in agreement with physical reality [10, 13]. On the other hand, the hydraulic diffusivity of the diffusion wave (Eq. 9-58) is independent of the Vedernikov number. Therefore, Eq. 9-81 is a better model than Eq. 9-58, especially for Froude numbers in the supercritical regime. Most natural flows, however, are in the range well below critical, with Eq. 9-58 remaining a practical model of unsteady open channel flow phenomena [7].
Las ecuaciones 9-78 y 9-81 proporcionan una capacidad de predicción mejorada para la simulación de las ondas de difusión que incluye un componente dinámico. Por ejemplo, para β = 1.5 (es decir, la fricción de Chezy en los canales amplios) y Fo = 2, el número de Vedernikov V = 1 (Eq. 9-80), y la difusividad hidráulica se desvanece, que está de acuerdo con la realidad física [10, 13]. Por otro lado, la difusividad hidráulica de la onda de difusión (Ec. 9-58) es independiente del número Vedernikov. Por lo tanto, la Ec. 9-81 es un modelo mejor que la Ec. 9-58, especialmente para números de Froude en el régimen supercrítico. La mayoría de los flujos naturales, sin embargo, están en el rango muy por debajo crítico, con la Ec. 9-58 restante a un modelo práctico de los fenómenos de flujo de canal abierto inestables [7].
PREGUNTAS
|
|
What is routing? What types of waves are used in describing unsteady open channel flow processes?
¿Cuál es el tránsito? ¿Qué tipos de ondas se utilizan en la descripción de los procesos de flujo de canales abiertos inestables?
What is model calibration? What is model verification?
¿Cuál es la calibración del modelo? ¿Qué es la verificación del modelo?
In the Muskingum method, what does the parameter K represent? What does the parameter X represent?
En el método de Muskingum, ¿qué representa el parámetro K? ¿Qué representa el parámetro X?
How does channel routing differ from reservoir routing? What differences are to be noted in the routed hydrographs?
¿Cómo difiere el tránsito del canal del tránsito de reservorio? ¿Qué diferencias se notan en los hidrogramas de tránsito?
What is the kinematic wave celerity? What is the practical range of turbulent flow values of β, the rating constant used in the kinematic wave celerity?
¿Qué es la celeridad de la onda cinemática? ¿Cuál es el alcance práctico de los valores de flujo turbulento de β, la constante de gasto utilizadas en la celeridad de la onda cinemática?
What is the order of accuracy of a numerical scheme? What is the difference between numerical diffusion and numerical dispersion in connection with kinematic wave solutions?
¿Cuál es el grado de exactitud de un esquema numérico? ¿Cuál es la diferencia entre la difusión numérica y dispersión numérica en relación con las soluciones de onda cinemática?
What is a linear model in the context of kinematic wave routing? What is a nonlinear model?
¿Qué es un modelo lineal en el contexto de tránsito de onda cinemática? ¿Qué es un modelo no lineal?
Why are the results of convex routing dependent on the grid size?
¿Por qué los resultados de tránsito convexo dependen del tamaño de la cuadrícula?
What is a diffusion wave? How does it differ from a kinematic wave?
¿Qué es una onda de difusión? ¿Cómo se diferencia de una onda cinemática?
What is hydraulic diffusivity? Why is it important in flood routing?
¿Cuál es la difusividad hidráulica? ¿Por qué es importante en el tránsito de avenidas?
What values of parameters X and C optimize numerical diffusion and minimize numerical dispersion in the Muskingum-Cunge method?
¿Qué valores de los parámetros X y C optimizan la difusión numérica y minimiza la dispersión numérica en el método de Muskingum-Cunge?
Why are negative values of X entirely possible in Muskingum-Cunge routing? Why are values of X in excess of 0.5 unfeasible?
¿Por qué son los valores negativos de X totalmente posibles en el tránsito de Muskingum-Cunge? ¿Por qué son los valores de X en exceso de 0.5 inviable?
What is the Courant number? What is the cell Reynolds number?
¿Qué es el número de Courant? ¿Cuál es la celda del número de Reynolds?
Describe the difference between linear and nonlinear solutions to channel routing problems.
Describir la diferencia entre las soluciones lineales y no lineales para los problemas de tránsito de canales.
What is a dynamic wave? How does it differ from the diffusion and kinematic waves?
¿Qué es una onda dinámica? ¿Cómo se diferencia de las ondas de difusión y cinemática?
How does the method of finite differences differ from the method of characteristics? What is a double sweep algorithm?
¿Cómo difiere el método de las diferencias finitas del método de las características? ¿Qué es un algoritmo de barrido doble?
Discuss the influence of the loop in the rating in determining whether an open channel flow wave is dynamic in nature.
Discutir la influencia del bucle en la calificación para determinar si una onda de flujo de canal abierto es de naturaleza dinámica.
What is the Vederkinov number? How does it differ from the Froude number?
¿Qué es el número Vederkinov? ¿En qué difiere del número de Froude?
What is the effect of the inclusion of a dynamic component in diffusion wave modeling?
¿Cuál es el efecto de la inclusión de un componente dinámico en el modelado de onda de difusión?
*****1610311730****
PROBLEMAS
|
|
Given the following inflow hydrograph to a certain stream channel reach, calculate the outflow by the Muskingum method. Check your results with ONLINE ROUTING 04.
Dado el siguiente hidrograma de flujo de entrada para un cierto tramo de canal de flujo, calcular el flujo de salida por el método de Muskingum. Comprobar los resultados con ONLINE ROUTING 04.
Time / Tiempo (h) 0 1 2 3 4 5 6 7 8 9 10 11 12 Flow / Flujo (m3/s) 10 20 40 80 120 150 120 60 50 40 30 20 10 Assume K = 1 h, X = 0.2, and Δt = 1 h.
Suponer K = 1 h, X = 0.2, and Δt = 1 h.
Given the following inflow hydrograph to a certain stream channel reach, calculate the outflow by the Muskingum method. Check your results with ONLINE ROUTING 04.
Dado el siguiente hidrograma de flujo de entrada para un cierto tramo de canal de flujo, calcular el flujo de salida por el método de Muskingum. Comprobar los resultados con ONLINE ROUTING 04.
Time / Tiempo (h) 0 3 6 9 12 15 18 21 24 27 30 33 36 Flow / Flujo (m3/s) 100 120 150 200 250 275 250 210 180 150 120 110 100 Assume K = 2.4 h, X = 0.1, and Δt = 3 h.
Asumir K = 2.4 h, X = 0.1, y Δt = 3 h.
Given the following inflow and outflow hydrographs for a certain stream channel reach, calculate the Muskingum parameters K and X.
Dados los siguientes hidrogramas de flujo de entrada y salida para un determinado tramo de canal de flujo, calcular los parámetros de Muskingum K y X.
Time / Tiempo (h) 0 1 2 3 4 5 Inflow / Flujo de Entrada (ft3/s ) 2520 3870 4560 6795 8975 9320 Outflow / Flujo de Salida (ft3/s ) 2520 2643 3598 4500 6367 8295 Time/ Tiempo (h) 6 7 8 9 10 11 Inflow / Flujo de Entrada (ft3/s ) 7780 6520 5340 4105 3210 2520 Outflow / Flujo de Salida (ft3/s ) 8900 7971 6808 5628 4439 3482 Time/ Tiempo (h) 12 13 14 15 16 17 Inflow / Flujo de Entrada (ft3/s ) 2520 2520 2520 2520 2520 2520 Outflow / Flujo de Salida (ft3/s ) 2782 2592 2540 2525 2521 2520 Develop a spreadsheet to solve the Muskingum method of stream channel routing, given the following data: (1) an inflow hydrograph of arbitrary shape, (2) baseflow, (3) storage constant K, (4) weighting factor X, and (5) time interval Δt. Test your spreadsheet with Example 9-1 in the text. Check your results with ONLINE ROUTING 04.
Desarrollar una hoja de cálculo para resolver el método de Muskingum de tránsito del canal de flujo, dados los siguientes datos: (1) un hidrograma de flujo de entrada de forma arbitraria, (2) el flujo de base, (3) constante de almacenamiento K, (4) factor de ponderación X, y (5) intervalo de tiempo Δt. Probar la hoja de cálculo con el Ejemplo 9-1 en el texto. Comprobar los resultados con ONLINE ROUTING 04.
Given the following inflow hydrograph, use the spreadsheet developed in Problem 9-4 to calculate the outflow hydrograph by the Muskingum method.
Dado el siguiente hidrograma de flujo de entrada, utilizar la hoja de cálculo desarrollado en el Problema 9-4 para calcular el hidrograma de flujo de salida por el método de Muskingum.
Time / Tiempo (h) 0.00 0.25 0.50 0.75 1.0 1.25 1.50 1.75 2.0 2.25 2.50 2.75 Flow / Flujo (m3/s) 0 1 2 4 8 10 8 6 4 2 1 0 Assume K = 0.4 h, X = 0.15, and Δt = 0.25 h. Check your results with ONLINE ROUTING 04.
Suponer K = 0.4 h, X = 0.15, y Δt = 0.25 h. Comprobar tus resultados ONLINE ROUTING 04.
Develop a spreadsheet to estimate the parameters of the Muskingum method, given a matching set of inflow and outflow hydrographs for a certain channel reach. A suggested algorithm is to search for the value of X that minimizes the root mean square (RMS) of the differences between predicted and measured storage. For this purpose, several values of X (between the range 0.0 to 0.5) are tried. For each trial value, a regression line is fitted to the (measured) storage (calculated using Eq. 9-7) versus weighted flow data, with weighted flow in the abscissas and measured storage in the ordinates. The differences between measured storage and predicted storage, i.e., storage predicted by the regression, are calculated. The RMS is evaluated by the following formula:
Desarrollar una hoja de cálculo para estimar los parámetros del método de Muskingum, dado un conjunto coincidente de hidrogramas de flujo entrada y salida para un determinado tramo de canal. Un algoritmo sugerido es para buscar el valor de X que reduce al mínimo la raíz cuadrada media (RMS) de las diferencias entre el almacenamiento previsto y medido. Para este fin, varios valores de X (entre el rango de 0.0 a 0.5) son juzgados. Para cada valor de prueba, una línea de regresión se monta en el almacenamiento (medido) (calculado usando la Ec. 9-7) frente a los datos de flujo ponderados, con el flujo ponderados en las en las abscisas y el almacenamiento medido en las ordenadas. Las diferencias entre el almacenamiento medido y almacenamiento predicho, es decir, el almacenamiento predicho por la regresión, se calculan. El RMS se evalúa por la siguiente fórmula:
1
RMS = [ ( ______ ) Σ (S - S' )2 ] 1/2
n - 1 n(9-82) in which S = measured storage, S' = predicted storage, and n = number of values. The X corresponding to the minimum RMS value is the estimated X. The Muskingum parameter K is the slope of the regression line corresponding to the chosen X value. Use Example 9-2 in the text to test your program.
en la que S = almacenamiento medido, S' = almacenamiento predicho, y n = número de valores. La X que corresponde al valor mínimo de RMS es el estimado X. El parámetro de Muskingum K es la pendiente de la línea de regresión correspondiente al valor elegido x. Usar el Ejemplo 9-2 en el texto para comprobar el programa.
Use the data of Problem 9-3 to test further the spreadsheet developed in Problem 9-6.
Utilizar los datos del problema 9-3 para poner a prueba aún más la hoja de cálculo desarrollado en el Problema 9-6.
Route the following flood wave using a linear forward-in-time/backward-in-space numerical scheme of the kinematic wave equation (similar to the convex method).
Transitar la siguiente onda de avenida mediante un esquema numérico adelante en tiempo/ hacia atrás en espacio lineal de la ecuación de onda cinemática (similar al método convexo).
Time / Tiempo (min) 0 10 20 30 40 50 60 70 80 90 100 Flow / Flujo (m3/s) 0 1 2 4 8 10 8 4 2 1 0 Assume baseflow 0 m3/s, V = 1m/s, β = 1.5, Δx = 1200 m, and Δt = 10 min.
Suponer que el flujo de base 0 m3/s, V = 1m/s, β = 1.5, Δx = 1200 m, and Δt = 10 min.
Derive the routing coefficients for a linear forward-in-space/ backward-in-time numerical scheme of the kinematic wave equation.
Derivar los coeficientes de tránsito para un esquema numérico hacia adelante en espacio/hacia atrás en tiempo lineal de la ecuación de onda cinemática.
Use the routing coefficients derived in Problem 9-9 to route the inflow hydrograph of Problem 9-8. Assume a reach length Δx = 800 m.
Utilizar los coeficientes de tránsito derivados en el Problema 9-9 para transitar el hidrograma de flujo de entrada el Problema 9-8. Asumir una longitud de tramo Δx = 800 m.
Calculate the β value for a triangular channel with Chezy friction.
Calcular el valor de β para un canal triangular con fricción Chezy.
A large river of nearly constant width B = 900 m is seen to be rising at the rate of 10 cm/h. At the observation point, a stage measurement indicates that the current value of discharge is 2200 m3/s. What is a rough estimate of the discharge at a point 5 km upstream?
Un gran río de la anchura casi constante B = 900 m se ve ir en aumento a un ritmo de 10 cm / h. En el punto de observación, una medición de nivel indica que el valor actual de la descarga es 2200 m3/s. ¿Cuál es una estimación aproximada de la descarga en un punto situado a 5 km aguas arriba?
Solve Problem 9-12 if the tributary contribution between the two points is estimated to be constant and equal to 225 m3/s.
Resolver el Problema 9-12 si se estima la contribución tributaria entre los dos puntos se estima ser constante e igual a 225 m3/s.
Determine if a flood wave with the following characteristics is a kinematic wave: time-of-rise tr = 6 h, bottom slope So = 0.015, average flow velocity Vo = 1.5 m/s, and average flow depth do = 3 m.
Determinar si una onda de avenida con las siguientes características es una onda cinemática: tiempo de subida tr = 6 h, pendiente del fondo So = 0.015, velocidad de flujo promedio Vo = 1.5 m/s, y profundidad de flujo promedio do = 3 m.
Determine if a flood wave with the following characteristics is a diffusion wave: time-of-rise
tr = 6 h, bottom slope So = 0.005, and average flow depthdo = 3 m. Determinar si una onda de avenida con las siguientes características es una onda de difusión: tiempo de subida
tr = 6 h, pendiente de fondo So = 0.005, y profundidad de flujo promediodo = 3 m. Program ONLINE_ROUTING_05 solves the Muskingum-Cunge method of flood routing, with routing parameters based on peak flow. Test this program using Example 9-9 in the text.
El programa ONLINE_ROUTING_05 resuelve el método de Muskingum-Cunge de tránsito de avenidas, con los parámetros de tránsito basado en el flujo máximo. Probar este programa usando el Ejemplo 9-9 en el texto.
Run ONLINE_ROUTING_05 using the following data: peak discharge = 500 m3/s, time-to-peak = 5 h, time base = 15 h, channel bed slope = 0.0008, flow area corresponding to the peak discharge = 200 m2, channel top width corresponding to the peak discharge = 50 m, rating exponent β = 1.65, reach length = 15 km, time interval Δt = 1 h. Report peak outflow and time-to-peak.
Ejecutar ONLINE_ROUTING_05 utilizando los siguientes datos: caudal máximo = 500 m3/s, el tiempo de pico = 5 h, tiempo base = 15 h, pendiente del lecho del canal = 0.0008, área de flujo correspondiente a la descarga máxima = 200 m 2, ancho superior del canal correspondiente a la descarga máxima = 50 m, exponente del gasto β = 1.65, longitud del tramo = 15 km, intervalo de tiempo Δt = 1 h. Report peak outflow and time-to-peak. Informar el flujo de salida máximo y el tiempo máximo.
Given the following inflow hydrograph to a stream channel reach, use ONLINE_ROUTING_05 to calculate the outflow hydrograph.
Dada la siguiente hidrograma de entrada a un canal de flujo de alcance, utilizar ONLINE_ROUTING_05 para calcular el hidrograma de salida.
Time / Tiempo (h) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Flow / Flujo (m3/s) 10 20 40 80 160 320 400 320 240 160 80 40 20 10 Assume channel bed slope = 0.001, flow area corresponding to the peak discharge = 800 m2, channel top width corresponding to the peak discharge = 35 m, rating exponent β = 1.6, reach length = 3 km, and time interval Δt = 1 h.
Suponer una pendiente del lecho del canal = 0.001,el área de flujo correspondiente a la descarga máxima = 800 m2, ancho superior del canal correspondiente a la descarga máxima = 35 m, el exponente de gasto β = 1.6, longitud del tramo = 3 km, y el intervalo de tiempo Δt = 1 h.
Given the following inflow hydrograph to a channel reach, calculate the outflow hydrographs for: (a) a reach length of 4 km, and (b) for a reach length of 5 km.
Dado el siguiente hidrograma de flujo de entrada a un tramo de canal, cálcular los hidrogramas de salida para: (a) longitud del tramo de 4 km, y (b) para una longitud de tramo de 5 km.
Time / Tiempo (h) 0 1 2 3 4 5 6 7 8 9 10 11 12 Flow / Flujo (m3/s ) 5 8 12 20 28 33 29 22 19 13 8 6 5 Assume channel bed slope = 0.0015, flow area corresponding to the peak discharge = 42 m2, channel top width corresponding to the peak discharge = 18 m, and rating exponent β = 1.5.
Asumir una pendiente del lecho del canal = 0.0015, área de flujo correspondiente a la descarga máxima = 42 m2, ancho superior del canal correspondiente a la descarga máxima = 18 m, y el exponente de gasto β = 1.5.
Calculate the hydraulic diffusivity for the following flow conditions: channel bed slope = 0.002, mean flow depth 4 m, mean flow velocity 2 m/s, and rating exponent β = 1.6. Compare the two cases: (a) without inertia, and (b) with inertia.
Calcular la difusividad hidráulica para las siguientes condiciones de flujo: pendiente del lecho del canal = 0.002, profundidad del flujo medio 4 m, velocidad de flujo medio de 2 m/s, y el exponente de gasto β = 1.6. Comparar los dos casos: (a) sin inercia, y (b) con la inercia.
BIBLIOGRAFÍA
|
|
Abbott, M. A. (1975). "Method of Characteristics," in Unsteady Flow in Open Channels, Vol. 1, K. Mahmood y V. Yevjevich, editors, Fort Collins, Colorado: Water Resources Publications.
Agricultural Research Service, U.S. Department of Agriculture. (1973). "Linear Theory of Hydrologic Systems," Technical Bulletin No. 1468, (J. C. 1. Dooge, author), Washington, D.C.
Crandall. S. H. (1956). Engineering Analysis. Engineering Society Monographs. New York: McGraw-Hill.
Cunge. J. A. (1969). "On the Subject of a Flood Propagation Computation Method (Muskingum Method)," Journal of Hydraulic Research. Vol. 7, No. 2, pp. 205-230.
Dooge, J. C. 1., W. B. Strupczewski, W.B. y J.J. Napiorkowski. (1982). "Hydrodynamic Derivation of Storage Parameters of the Muskingum Model," Journal of Hydrology. Vol. 54, pp. 371-387.
Fread, D. L. (1985). "Channel Routing," in Hydrological Forecasting. M. G. Anderson y T. P. Burt, editors. New York: John Wiley.
Hayami, S. (1951). "On the Propagation of Flood Waves," Bulletin of the Disaster Prevention Research Institute. Kyoto University, Kyoto, Japan, No.1, diciembre.
Kleitz, M. (1877). "Note sur la Theorie du Mouvement non Permanent des Liquides et sur application a la Propagation del Crues des Rivieres, (Note on the Theory of Unsteady Flow of Liquids and on Application to Flood Propagation in Rivers)," Annales des Ponts et Chaussees, Ser. 5, Yol. 16, 2e semestre, pp. 133-196.
Liggett, J. A., y I. A. Cunge. (1975). "Numerical Methods of Solution of the Unsteady Flow Equations," in Unsteady Flow in Open Channels. Yol. 1, K. Mahmood y V. Yevjevich, editors. Fort Collins, Colorado: Water Resources Publications.
Lighthill, M. J., y G. B. Whitham. (1955). "On Kinematic Waves. I. Flood Movement in Long Rivers," Proceedings of the Royal Society of London. Vol. A229, mayo, pp. 281-316.
McCarthy, G. T. (1938). "The Unit Hydrograph and Flood Routing," unpublished manuscript, presented at a Conference of the North Atlantic Division, U.S. Army Corps of Engineers, junio 24.
Natural Environment Research Council. (1975). Flood Studies Report. Vol. 3: Flood Routing. London. England.
Ponce, V. M., and D. B. Simons. (1977). "Shallow Wave Propagation in Open Channel Flow," Journal of the Hydraulics Division, ASCE, Vol. 103, No. HYI2, diciembre, pp. 1461-1476.
Ponce, V. M., R. M. Li, y D. B. Simons. (1978). "Applicability of Kinematic and Diffusion Models." Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY3, marzo, pp. 353-360.
Ponce, V. M., y V. Yevjevich. (1978). "Muskingum-Cunge Method with Variable Parameters," Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY12, diciembre, pp. 1663-1667.
Ponce, V. M., y F. D. Theurer. (1982). "Accuracy Criteria in Diffusion Routing," Journal of the Hydraulics Division, ASCE, Vol. 108, No. HY6, junio, pp. 747-757.
Ponce, V. M. (1991). "New perspective on the Vedernikov number," Water Resources Research, Vol. 27, No. 7, julio, pp. 1777-1779.
Roache. P. (1972). Computational Fluid Dynamics. Hermosa Publishers, New Mexico: Albuquerque.
Seddon, J. A. (1900). "River Hydraulics," Transactions, ASCE, Vol. 43, pp. 179-229.
Woolhiser. M. H., y J. A. Liggett. (1967). "Unsteady One-Dimensional Flow Over a Plane: The Rising Hydrograph." Water Resources Research. Vol. 3, No. 3, pp. 753-771.
SUGGESTED READINGS
Agricultural Research Service, U.S. Department of Agriculture. (1973). "Linear Theory of Hydrologic Systems." Technical Bulletin No. 1468, (J. C. I. Dooge, author), Washington, D.C.
Cunge, J. A. (1969). "On the Subject of a Flood Propagation Computation Method (Muskingum Method)." Journal of Hydraulic Research, Vol. 7. No.2. 1969, pp. 205-230.
Fread, D. L. (1985). "Channel Routing," in Hydrological Forecasting, M. G. Anderson and T. P. Burt, editors, New York: John Wiley.
Fread, D. L. (1993). "Flow Routing," Chapter 10 in Handbook of Hydrology, D. R. Maidment, editor, New York: McGraw-Hill.
Lighthill, M.J., and Whitham. G. B. (1955). "On Kinematic Waves. I. Flood Movement in Long Rivers," Proceedings of the Royal Society of London, Vol. A229, maio, pp. 281-316.
Natural Environment Research Council. (1975). Flood Studies Report. Vol. 5: Flood Routing, London, England, 1975.
| http://engineeringhydrology.sdsu.edu |
|
180925 16:00 |