|
|
|
CHAPTER 10: TRÁNSITO EN CUENCAS |
|
"We give a mathematical treatment of the 'competition' between kinematic and dynamic waves in river flow, in order to show how completely the dynamic waves are subordinated in the case of greatest interest, that is, when the speed of the river is well below critical."
"Damos un tratamiento matemático de la 'competencia' entre las ondas cinemáticas y
dinámicas en el caudal de los ríos,
con el fin de mostrar cuán completamente las ondas dinámicas están
subordinados en el caso de mayor interés,
es decir, cuando la velocidad del río está muy por debajo de lo crítico."
| M. J. Lighthill and G. B. Whitham (1955) |
|
This chapter is divided into six sections. Section 10.1 describes the time-area method of hydrologic catchment routing. Section 10.2 describes the Clark unit hydrograph, a procedure closely related to the time-area method. Section 10.3 deals with the cascade of linear reservoirs, a widely accepted method of hydrologic catchment routing. Sections 10.4 and 10.5 describe two hydraulic methods of catchment routing, based on kinematic and diffusion waves, respectively. Section 10.6 contains a discussion of the capabilities and limitations of catchment routing techniques. Este capítulo se divide en seis secciones. La Sección 10.1 describe el método de tiempo-espacio del tránsito de cuencas hidrológicas. La Sección 10.2 describe el hidrograma unitario de Clark, un procedimiento muy relacionado con el método de tiempo-área. La Sección 10.3 se refiere a la cascada de embalses lineales, un método ampliamente aceptado en el tránsito de cuencas hidrológicas. Las Secciones 10.4 y 10.5 describen dos métodos hidráulicos de tránsito de cuencas, basado en la cinemática y ondas de difusión, respectivamente. La Sección 10.6 contiene un análisis de las capacidades y limitaciones de las técnicas de tránsito de cuencas. |
10.1 EL MÉTODO DE TIEMPO-ÁREA
|
|
Catchment Routing / tránsito de cuencas
Catchment routing refers to the calculation of flows in time and space within a catchment. The objective of catchment routing is to transform effective rainfall into streamflow. This is accomplished either in a lumped mode (e.g., time-area method) or in a distributed mode (e.g., kinematic wave method).
El tránsito de cuencas se refiere al cálculo de los flujos en el tiempo y espacio dentro de una cuenca. El objetivo de tránsito de cuencas es transformar la precipitación efectiva en caudal. Esto se logra ya sea en un modo agrupado (por ejemplo, el método de tiempo-área) o en un modo distribuido (por ejemplo, el método de la onda cinemática).
Methods for catchment routing are similar to those of reservoir and stream channel routing. In fact, many techniques used in reservoir and channel routing are also applicable to catchment routing. For instance, the concept of linear reservoir is used in both reservoir and catchment routing. Kinematic wave techniques were originaIly developed for river routing [9], but later were applied to catchment routing [20, 23].
Los métodos para el tránsito de cuencas son similares a los del reservorio y el enrutamiento del canal de flujo. De hecho, muchas de las técnicas utilizadas en el reservorio y el enrutamiento del canal son también aplicables al tránsito de cuencas. Por ejemplo, el concepto de reservorio lineal se utiliza tanto en el reservorio y en el tránsito de cuencas. Las técnicas de onda cinemática se desarrollaron originalmente para el enrutamiento del río [9], pero más tarde se aplicaron al tránsito de cuencas [20, 23].
Methods for catchment routing are of two types: (1) hydrologic and (2) hydraulic. Hydrologic methods are based on the storage concept and are spatially lumped to provide a runoff hydrograph at the catchment outlet. Examples of hydrologic catchment routing methods are the time-area method and the cascade of linear reservoirs. Hydraulic methods use kinematic or diffusion waves to simulate surface runoff within a catchment in a distributed context. Unlike hydrologic methods, hydraulic methods can provide runoff hydrographs inside the catchment.
Los métodos para el tránsito de cuencas son de dos tipos: (1) hidrológico e (2) hidráulico. Los métodos hidrológicos se basan en el concepto de almacenamiento y se agrupan espacialmente para proporcionar un hidrograma de escorrentía en la salida de la cuenca. Los ejemplos de los métodos de tránsito de cuencas hidrológica son el método de tiempo-área y la cascada de reservorios lineales. Los métodos hidráulicos utilizan ondas cinemáticas o de difusión para simular la escorrentía superficial dentro de una cuenca en un contexto distribuido. A diferencia de los métodos hidrológicos, los métodos hidráulicos pueden proporcionar hidrogramas de escorrentía dentro de la cuenca.
Catchment routing models can use parametric, conceptual, and / or deterministic components. For instance, the hydrograph obtained by the time-area method can be routed through a linear reservoir using a storage constant derived by empirical (i.e., parametric) means. The cascade of linear reservoirs is a typical example of a conceptual model used in catchment routing. Kinematic and diffusion models are examples of deterministic methods used in catchment routing.
Los modelos de tránsito de cuencas pueden utilizar componentes paramétricos, conceptuales, y/o deterministas. Por ejemplo, el hidrograma obtenido por el método de tiempo-área puede ser enrutado a través de un reservorio lineal utilizando una constante de almacenamiento derivado por medios (es decir, paramétrica) empíricos. La cascada de reservorios lineales es un ejemplo típico de un modelo conceptual utilizado en el tránsito de cuencas. Los modelos cinemáticos y de difusión son ejemplos de métodos deterministas utilizados en el tránsito de cuencas.
The concepts of translation and storage are central to the study of flow routing, whether in catchments, reservoirs, or stream channels. They are particularly important in catchment routing, because they can be studied separately. Translation may be interpreted as the movement of water in a direction parallel to the channel bottom. Storage may be interpreted as the movement of water in a direction perpendicular to the channel bottom. Translation is synonymous with runoff concentration; storage is synonymous with runoff diffusion.
Los conceptos de traducción y almacenamiento son fundamentales para el estudio del enrutamiento de flujo, ya sea en las cuencas, reservorios o canales de corriente. Son particularmente importantes en el tránsito de cuencas, debido a que pueden ser estudiadas por separado. La traducción puede ser interpretada como el movimiento del agua en una dirección paralela a la parte inferior del canal. El almacenamiento puede ser interpretado como el movimiento del agua en una dirección perpendicular a la parte inferior del canal. La traducción es sinónimo de concentración de la escorrentía; el almacenamiento es sinónimo de difusión de la escorrentía.
In reservoir routing, storage is the primary mechanism, with translation almost nonexistent. In stream channel routing, the situation is reversed, with translation being the predominant mechanism and storage playing only a minor role. This is the reason why kinematic and diffusion waves are useful models of stream channel routing. In catchment routing, translation and storage are about equally important and, therefore, they are often accounted for separately. The translation effect can be related to runoff concentration, whereas the storage effect can be simulated with linear reservoirs.
En el enrutamiento del reservorio, el almacenamiento es el mecanismo primario, con traducción casi inexistente. El enrutamiento del canal del arroyo, la situación se invierte, con traducción de ser el mecanismo predominante y el almacenamiento juega un papel menor. Esta es la razón por la cual las ondas cinemáticas y de difusión son modelos útiles de enrutamiento del canal del arroyo. En el tránsito de cuencas, la traducción y el almacenamiento son casi igual de importantes y, por lo tanto, a menudo se contabilizan por separado. El efecto de la traducción puede estar relacionada con la concentración de la escorrentía, mientras que el efecto de almacenamiento puede ser simulado con depósitos lineales.
Time-Area Method / Método del Tiempo-Área
The time-area method of hydrologic catchment routing transforms an effective storm hyetograph into a runoff hydrograph. The method accounts for translation only and does not include storage. Therefore, hydrographs calculated with the time-area method show a lack of diffusion, resulting in higher peaks than those that would have been obtained if storage had been taken into account. If necessary, the required amount of storage can be incorporated by routing the hydrograph obtained by the time-area method through a linear reservoir. The required amount of storage is determined by calibrating the linear reservoir storage constant K with measured data. Alternatively, suitable values of K can be estimated based on regionally derived formulas.
El método de tiempo-espacio de tránsito de cuencas hidrológica transforma un hietograma de tormenta efectiva en un hidrograma de escorrentía. El método representa una traducción solamente y no incluye el almacenamiento. Por lo tanto, los hidrogramas calculados con el método de tiempo-área muestran una falta de difusión, lo que resulta en los picos más altos que los que se habrían obtenido si el almacenamiento se hubiera tenido en cuenta. Si es necesario, la cantidad requerida de almacenamiento puede ser incorporada por el enrutamiento del hidrograma obtenido por el método de tiempo-área a través de un reservorio lineal. La cantidad requerida de almacenamiento se determina mediante la calibración de la constante K del almacenamiento del reservorio lineal con los datos medidos. Alternativamente, los valores adecuados de K se pueden estimar en base a fórmulas derivadas regionalmente.
The time-area method is essentially an extension of the runoff concentration principle used in the rational method (Chapter 4). Unlike the rational method, however, the time-area method can account for the temporal variation of rainfall intensity. Therefore, the applicability of the time-area method is extended to midsize catchments.
El método de tiempo-área es esencialmente una extensión del principio de concentración de escorrentía utilizado en el método racional (Capítulo 4). A diferencia del método racional, sin embargo, el método de tiempo-área puede dar cuenta de la variación temporal de intensidad de lluvia. Por lo tanto, la aplicabilidad del método de tiempo-área se extiende a las cuencas de tamaño medio.
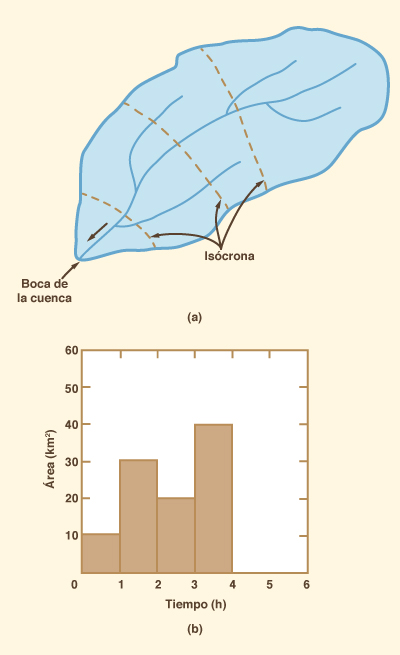
The time-area method is based on the concept of time-area histogram, i.e., a histogram of contributing catchment subareas. To develop a time-area histogram, the catchment's time of concentration is divided into a number of equal time intervals. Cumulative time at the end of each time interval is used to divide the catchment into zones delimited by isochrone lines, i.e., the loci of points of equal travel time to the catchment outlet, as shown in Fig. 10-1 (a). For any point inside the catchment, the travel time refers to the time that it would take a parcel of water to travel from that point to the outlet. The catchment subareas delimited by the isochrones are measured and plotted in histogram form as shown in Fig. 10-1 (b).
El método de tiempo-área se basa en el concepto del histograma tiempo-área, es decir, un histograma contribuyendo subáreas de captación. Para desarrollar un histograma de tiempo-área, el tiempo de la captación de concentración se divide en un número de intervalos de tiempo iguales. El tiempo acumulado al final de cada intervalo de tiempo se utiliza para dividir la cuenca en zonas delimitadas por líneas isócronas, es decir, los lugares geométricos de los puntos de tiempo de viaje igual a la salida de captación, como se muestra en la Fig. 10-1 (a). Para cualquier punto dentro de la cuenca, el tiempo de viaje se refiere al tiempo que tomaría una parcela de agua para viajar desde ese punto a la salida. Las subáreas de captación delimitadas por las isócronas se miden y se representan gráficamente en forma de histograma, como se muestra en la Fig. 10-1 (b).
Figure 10-1 Método tiempo-área: (a) delineación isócrona; (b) histograma tiempo-área. |
The time interval of the effective rainfall hyetograph must be equal to the time interval of the time-area histogram. The rationale of the time-area method is that, according to the runoff concentration principle (Section 2.4), the partial flow q at the end of each time interval is equal to the product of effective rainfall i times contributing subarea a, i.e., q = ia. The lagging and summation of the partial flows results in a runoff hydrograph for the given effective rainfall hyetograph and time-area histogram.
El intervalo de tiempo del hietograma de precipitación efectiva debe ser igual al intervalo de tiempo del histograma de tiempo- área. El fundamento del método del tiempo-área es que, de acuerdo con el principio de concentración de escorrentía (Sección 2.4), el flujo parcial q al final de cada intervalo de tiempo es igual al producto de la precipitación efectiva i por la subárea contribuyente a, es decir, q = ia. El retraso y la suma de las corrientes parciales resulta en un hidrograma de escorrentía para el hietograma de precipitación efectiva dada y el histograma de tiempo-área.
While the time-area method accounts for runoff concentration only, it has the advantage that the catchment shape is reflected in the time-area histogram and, therefore, in the runoff hydrograph. The procedure is illustrated by the following example.
Mientras que el método de tiempo-área representa la concentración de la escorrentía solamente, tiene la ventaja de que la forma de captación se refleja en el histograma de tiempo-área y, por lo tanto, en el hidrograma de escorrentía. El procedimiento se ilustra mediante el siguiente ejemplo.
Ejemplo 10-1.
A 100-km2 catchment has a 4-h time of concentration, with isochrones at 1-h intervals resulting in the
time-area histogram shown in Fig. 10-1 (b).
A 6-h storm has the following effective rainfall hyetograph
Una cuenca de captación de 100-km2 tiene un tiempo de concentración
de 4-h, con isócronas a intervalos de 1-h resultando el histograma de tiempo-área
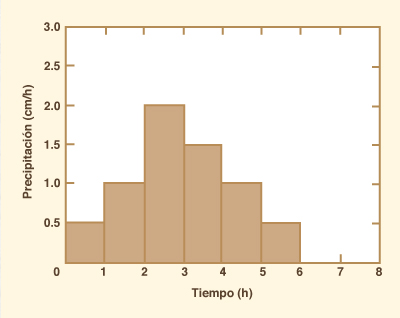
mostrado en la Fig. 10-1 (b). Una tormenta de 6-h tiene el siguiente hietograma de precipitación efectiva (Fig 10-2.):
Figure 10-2 Hietograma de precipitación efectiva: Ejemplo 10-1.
Use the time-area method to calculate the outflow hydrograph.
Utilizar el método tiempo-área para calcular el hidrograma de salida.
The routing is shown in Table 10-1.
El enrutamiento se muestra en la Tabla 10-1.
Column 1 shows time in hours.
La Columna 1 muestra el tiempo en horas.
The flows shown in Cols. 2-7 were obtained by multiplying effective rainfall intensity times the confributing
partial area.
For instance, Col. 2 shows the contribution of the first effective rainfall interval (0.5 cm/h) on each of the
subareas (10, 30, 20, and 40 km2).
At t = 1 h, the partial flow due to the first effective rainfall interval is: 0.5 cm/h × 10 km2 =
5 km2-cm/h (i.e., the flow contributed by the subarea enclosed within the catchment outlet and the first
isochrone takes 1 h to concentrate).
Likewise, at t = 2 h, the partial flow due to the first effective rainfall interval is: 0.5 cm/hr × 30 km2 =
Los flujos mostrados en las Columnas 2-7 fueron obtenidos multiplicando la intensidad de precipitación
efectiva por el área parcial contribuyente.
Por ejemplo, Col. 2 muestra la contribución del primer intervalo de precipitación efectiva
(0.5 cm/h) en cada una de las subáreas (10, 30, 20, and 40 km2).
En t = 1 h, el flujo parcial debido al primer intervalo de precipitación efectiva es:
0.5 cm/hr × 30 km2 =
The remaining values in Col. 2 (10 and 20) are calculated in a similar way.
Finally, at t = 5 h, the flow is zero because it takes a full time interval (in the absence of runoff diffusion)
for the last concentrated partial flow to recede back to zero.
Los valores restantes en la Col. 2 (10 y 20) se calculan de forma similar.
Por último, en t = 5 h, el flujo es cero debido a que se necesita un intervalo de tiempo completo (en ausencia de difusión de la escorrentía) para el último
flujo parcial concentrado a retroceder de nuevo a cero.
Columns 2 to 7 show the partial flows contributed by the six effective rainfall intervals, each appropriately lagged a
time interval (because the contribution of the second rainfall interval starts at
Las columnas 2 a 7 muestran los flujos parciales aportados por los seis intervalos
de precipitación efectiva, cada retraso apropiadamente a un intervalo de tiempo
(debido a la contribución del segundo intervalo de la precipitación comienza en
The sum of these partial flows, shown in Col. 8, is the catchment outflow hydrograph.
La suma de estos flujos parciales, se muestra en la Col. 8, es el hidrograma de salida de captación.
In Col. 9, the hydrograph of Col. 8 is expressed in cubic meters per second (Col. 8 × 2.78).
En la Col. 9, el hidrograma de la Col. 8 se expresa en metros cúbicos por
segundo (Col. 8 × 2.78).
The time base of the outflow hydrograph is 10 h, which is equal to the time of
concentration (4 h) plus the effective
rainfall duration (6 h).
La base de tiempo del hidrograma de salida es de 10 h, que es igual al tiempo de
concentración (4 h) además de la duración de precipitación efectiva (6 h).
To verify the accuracy of the computations, the sum of Col. 8 is 650 km2-cm/h, which represents 6.5 cm
of effective rainfall depth uniformly distributed over the entire catchment area (100 km2).
This value (6.5 cm) agrees with the total amount of effective rainfall.
Para verificar la exactitud de los cálculos, la suma de Col. 8 es de
km2-cm/h, lo que representa 6.5 cm de profundidad de precipitación efectiva
uniformemente distribuida sobre toda el área de captación
(100 km2). Este valor (6.5 cm) de acuerdo
con la cantidad total de precipitación efectiva.
ONLINE CALCULATION.
Using ONLINE ROUTING06, the
result is esentially the same as that of Col. 9, Table 10-1.
CALCULADORA EN LÍNEA.
Usando ONLINE ROUTING06, el resultado es
esencialmente el mismo que el de la Col. 9, Tabla 10-1.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
It is readily seen that the time-area method and the rational method (Chapter 4) share a common theoretical basis. However, since the time-area method uses effective rainfall and does not rely on runoff coefficients, it can account only for runoff concentration, with no provision for runoff diffusion. Diffusion can be provided by routing the hydrograph calculated by the time-area method through a linear reservoir with an appropriate storage constant.
Se ve fácilmente que el método de tiempo-área y el método racional (Capítulo 4) comparten una base teórica común. Sin embargo, ya que el método de tiempo-área utiliza la precipitación efectiva y no se basa en los coeficientes de escorrentía, se puede explicar sólo por la concentración de la escorrentía, con ninguna disposición para la difusión de escorrentía. La difusión puede ser proporcionada por el encaminamiento del hidrograma calculado por el método de tiempo-área a través de un reservorio lineal con una constante de almacenamiento apropiado.
Tiempo de concentración. The time-area method leads to an alternate way of calculating time of concentration. Provided there is no runoff diffusion as would be the case of a hydrograph calculated by the time-area method, time of concentration can be calculated as the difference between hydrograph time base and effective rainfall duration. Intuitively, as rainfall ceases, the farthest parcels of water concentrate at the catchment outlet at a time equal to the time of concentration. Therefore:
El método de tiempo-área lleva a una forma alternativa de calcular el tiempo de la concentración. Siempre que no haya difusión de escorrentía como sería el caso de un hidrograma calculado por el método de tiempo-área, el tiempo de concentración se puede calcular como la diferencia entre la base de tiempo del hidrograma y la duración de precipitación efectiva. Intuitivamente, como la precipitación cesa, las parcelas más lejanas del agua se concentran en la salida de captación en un tiempo igual al tiempo de concentración. Por consiguiente:
| tc = Tb - tr | (10-1) |
in which tc = time of concentration, Tb =
time base of the translated-only hydrograph, and
en el que tc = tiempo de concentración,
Tb = base de tiempo del hidrograma traducido únicamente, y
Equation 10-1 can also be expressed in a slightly different form.
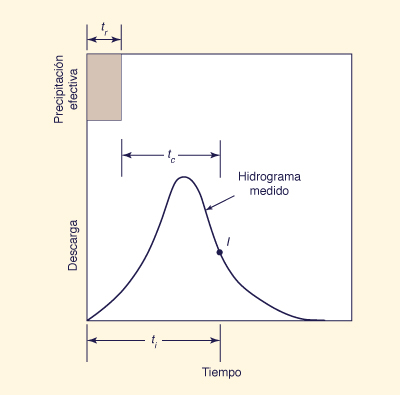
Assuming that the point of inflection (i.e., the point of zero curvature) on the receding
limb of a measured (i.e., translated and diffused) hydrograph coincides with the end of the translated-only hydrograph, the time to point of inflection of the measured hydrograph can be used in
La ecuación 10-1 también se puede expresar en una forma ligeramente diferente.
Suponiendo que el punto de inflexión (es decir, el punto de curvatura cero)
la extremidad del retroceso de un hidrograma medido (es decir, traducido y difundido)
coincide con el final de un hidrograma traducido solamente, el tiempo hasta el punto de
inflexión del hidrograma medido se puede utilizar en la
| tc = ti - tr | (10-2) |
in which ti = time to point of inflection on the receding limb of a measured hydrograph. The advantage of Eq. 10-2 over Eq. 10-1 is that, unlike the time base of the translated-only hydrograph, the point of inflection on the receding limb of a measured hydrograph can be readily ascertained.
en el que ti = tiempo al punto de inflexión en la extremidad del retroceso de un hidrograma medido. La ventaja de la Ec. 10-2 sobre la Ec. 10-1 es que, a diferencia de la base de tiempo del hidrograma traducido solamente, el punto de inflexión en la extremidad del retroceso de un hidrograma medido puede determinarse fácilmente.
Figura 10-3 Definición alterna del tiempo de concentración. |
10.2 EL HIDROGRAMA UNITARIO DE CLARK
|
|
The procedure to derive a Clark unit hydrograph parallels that of the time-area method [2]. First, it is necessary to determine the catchment isochrones. In the Clark method, however, a unit effective rainfall is used in lieu of the effective storm hyetograph used in the time-area method. This leads to an outflow hydrograph corresponding to a unit runoff depth, that is, a unit hydrograph. Since the unit hydrograph calculated in this way lacks (runoff) diffusion, Clark suggested that it be routed through a linear reservoir.
El procedimiento para derivar un hidrograma unitario Clark paralelo al método de tiempo-área [2]. En primer lugar, es necesario determinar las isócronas de captación. En el m&ecute;todo de Clark, sin embargo, una unidad de precipitación efectiva se utiliza en lugar de un hidrograma de tormenta efectiva usado en el método tiempo-área. Esto conduce a un hidrograma de salida correspondiente a una profundidad de escorrentía unitaria, esto es, un hidrograma unitario. Desde el hidrograma unitario calculado de esta manera carece de difusión (escorrentía), Clark sugirió que se encamina a través de un reservorio lineal.
As with the time-area method, an estimate of the linear reservoir storage constant is required. This can be obtained either from the tail of a measured hydrograph or by using a regionally derived formula. In the latter case, the Clark unit hydrograph can be properly regarded as a synthetic unit hydrograph.
Al igual que con el método de tiempo-área, se requiere una estimación de la constante de almacenamiento de un reservorio lineal. Esto puede conseguirse a través de la cola de un hidrograma medido o mediante el uso de una fórmula derivada regionalmente. En este último caso, el hidrograma unitario de Clark puede considerarse propiamente como un hidrograma unitario sintético.
Like the time-area method, the Clark unit hydrograph method has the advantage that the catchment's properties (shape, hydraulic length, surface roughness, and so on) are reflected in the time-area histogram and, therefore, on the shape of the unit hydrograph. This feature has contributed to the popularity of the Clark unit hydrograph in engineering practice [7].
Al igual que el método de tiempo-área, el método del hidrograma unitario de Clark tiene la ventaja de que las propiedades de captación (forma, longitud hidráulica, rugosidad de la superficie, y así sucesivamente) se reflejan en el histograma de tiempo-área y, por tanto, en la forma del hidrograma unitario. Esta característica ha contribuido a la popularidad del hidrograma unitario de Clark en la práctica de la ingeniería [7].
When using the Clark or time-area methods, the storage constant can be estimated from the tail of a measured hydrograph. For this purpose, the differential equation of storage (Eq. 8-4) is evaluated at a time for which inflow equals zero (I = 0), i.e., past the end of the translated-only hydrograph. Alternatively, it can be evaluated at the point of inflection on the receding limb of a measured hydrograph (Fig. 10-3). This leads to:
Cuando se utilizan los métodos de Clark o tiempo-área, la constante de almacenamiento puede estimarse a partir de la cola de una hidrograma medido. Para este propósito, la ecuación diferencial de almacenamiento (Ec. 8-4) se evalúa a la vez para que el flujo de entrada es igual a cero ( I = 0), es decir, más allá del final del hidrograma traducido solamente. Alternativamente, se puede evaluar en el punto de inflexión en la extremidad del retroceso de un hidrograma medido (Fig. 10-3). Esto lleva a:
|
dS - O = _____ dt | (10-3) |
and since S = KO, the following expression for K is obtained:
y puesto que S = KO , la siguiente expresión para K se obtiene:
|
O K = - ________ dO _____ dt | (10-4) |
in which O and dO/dt are evaluated past the end of the translated-only hydrograph or at (the time to) the point of inflection on the receding limb of a measured hydrograph.
en el que O y do / dt se evalúan más allá del final del hidrograma trasladado solamente o al (el tiempo para) el punto de inflexión en la extremidad del retroceso de un hidrograma medido.
The derivation of the Clark unit hydrograph is illustrated by the following example.
La derivación del hidrograma unitario de Clark se ilustra mediante el siguiente ejemplo.
Example 10-2.
Use the Clark method to derive a 2-h unit hydrograph for the catchment of Example 10-1.
To provide storage, route the translated-only hydrograph through a linear reservoir of storage constant K = 2 h.
Use
Utilizar el método de Clark para derivar un hidrograma unitario de 2-h para la cuenca del
Ejemplo 10-1.
Para proporcionar el almacenamiento, la ruta del hidrograma trasladado solamente
a través de un reservorio lineal de almacenamiento constante K = 2 h.
Usar
The 2-h unit hydrograph has an effective rainfall intensity of 0.5 cm/h (i.e., 1-cm depth distributed over a 2-h duration).
The calculations are shown in Table 10-2.
El hidrograma unitario de 2-h tiene una intensidad de precipitación efectiva de
0.5 cm/h (es decir, profundidad de 1-cm distribuída sobre una duración de 2-h).
Los cálculos se muestran en la Tabla 10-2.
Column 1 shows time in hours.
La columna 1 muestra el tiempo en horas.
Column 2 shows the contribution of the first hour, with 0.5 cm/h of effective rainfall.
The procedure is the same as in Table 10-1, Col. 2.
La columna 2 muestra la contribución de la primera hora, con 0.5 cm/h de
precipitación efectiva.
El procedimiento es el mismo que en la Tabla 10-1, Col. 2.
Column 3 shows the contribution of the second hour, with 0.5 cm/h of effective rainfall.
Again, the procedure is the same as in Table 10-1, Col. 2; but the partial flows are lagged 1 h.
La columna 3 muestra la contribución de la segunda hora, con 0.5 cm/h
de precipitación efectiva. Una vez más, el procedimiento es el mismo
que en la Tabla 10-1, Col. 2; pero los flujos parciales se retrasan 1 h.
The translated-only unit hydrograph shown in Col. 4 is the sum of the partial flows (Cols. 2 and 3).
The translated-only unit hydrograph (Col. 4) is the inflow to the linear reservoir.
With Δt/K = 1/2, the routing coefficients (Table 8-1) are C0 = 1/5,
C1 = 1/5, and C2 = 3/5.
El hidrograma unitario trasladado únicamente mostrado en la Col. 4 es la suma de los
flujos parciales (Cols. 2 y 3).
El hidrograma unitario trasladado únicamente (Col. 4) es la entrada de flujo al
reservorio lineal.
Con Δt/K = 1/2, los
coeficientes de enrutamiento (Tabla 8-1) son C0 = 1/5,
C1 = 1/5, and C2 = 3/5.
The partial flows of the linear reservoir routing are shown in Cols. 5 to 7, and the translated-and-diffused unit hydrograph (in km2-cm/h) shown in Col. 8 is the sum of Cols. 5 to 7
(See Example 8-1 for details of the linear reservoir routing procedure).
Los flujos parciales del enrutamiento del reservorio lineal se muestran en las
Cols. 5 a 7, y el hidrograma unitario trasladado y difundido (en km2-cm/h)
mostrados en la Col.8 es la suma de las Cols. 5 a 7
(Véase el Ejemplo 8-1 para los detalles del procedimiento de enrutamiento del
reservorio lineal).
Column 9 shows the translated-and-diffused Clark unit hydrograph in cubic meters per second.
La columna 9 muestra el hidrograma unitario trasladado y difundido de Clark
en metros cúbicos por segundo.
The sum of the ordinates of the translated-only hydrograph (Col. 4) is 100,
which amounts to 1 cm of effective rainfall depth uniformly distributed over 100 km2 of catchment area.
Likewise, the sum of the ordinates of the translated-and-diffused hydrograph (Col. 8) is 99.98, which verifies not only that the calculated hydrograph is a unit hydrograph but also that the calculation is mass (i.e., volume) conservative.
La suma de las ordenadas del hidrograma trasladado solamente (Col. 4) es de 100,
lo que equivale a 1 cm de profundidad de precipitación efectiva uniformemente
distribuida sobre 100 km2 de área de captación.
Del mismo modo, la suma de las ordenadas del hidrograma trasladado y difuso (Col. 8) es 99.98,
que verifica no solamente que
el hidrograma calculado es un hidrograma unitario, sino también que el cálculo
es la masa (es decir, volumen) conservadora.
Note that the peak of the translated-only unit hydrograph (Col. 4) is 30 km2-cm/h,
whereas the peak of the translated-and-diffused unit hydrograph (Col. 8) is 21.05 km2-cm/h.
Also, note that the time base of the translated-only unit hydrograph ends sharply at 6 h, whereas the time base of the
translated-and-diffused unit hydrograph is much longer, with the receding limb of
the unit hydrograph gradually approaching zero.
This reveals the substantial amount of runoff diffusion provided by the linear reservoir.
Nótese que el pico del hidrograma unitario trasladado únicamente (Col. 4) es
30 km2-cm/h,
mientras que el pico del hidrograma unitario trasladado y difuso (Col. 8) es de 21.05
km2-cm/h.
Además, nótese que la base de tiempo del hidrograma unitario trasladado
únicamente termina abruptamente a las 6 h, mientras que la base de tiempo del
hidrograma unitario trasladado y difuso es mucho más largo, con la extremidad del retroceso
del hidrograma unitario acercándose gradualmente a cero.
Esto revela la cantidad sustancial de la difusión de escorrentía proporcionada
por el reservorio lineal.
ONLINE CALCULATION.
Using ONLINE ROUTING07, the
result is esentially the same as that of Col. 9, Table 10-2.
CÁLCULO EN LÍNEA.
Utilizando LÍNEA ROUTING07 ,
el resultado es esencialmente el mismo que el de Col. 9, Tabla 10-2.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Important Note. In the Clark method, the number of partial flows (two in Example 10-2, shown as Cols. 2 and 3 of Table 10-2) is equal to the duration of the unit hydrograph (2 h) divided by the (chosen) time interval of histogram definition
(1 h). Also, in Example 10-2, the unit effective rainfall intensity (0.5 cm/h) is equal to the unit rainfall depth (1 cm) divided by the duration of the unit hydrograph(2 h). Nota importante. En el método de Clark, el número de flujos parciales (dos en el Ejemplo 10-2, muestra como las Cols. 2 y 3 de la Tabla 10-2) es igual a la duración del hidrograma unitario (2 h) dividido por el (elegido) intervalo de tiempo de la definición del histograma
(1 h). Además, en el Ejemplo 10-2, la intensidad de la precipitación efectiva unitaria (0.5 cm/h) es igual a la profundidad de precipitación unitaria (1 cm) dividido por la duración del hidrograma unitario (2 h).
By using Eq. 10-4, the linear reservoir storage constant can be calculated directly from the tail of a measured hydrograph.
To illustrate the procedure, in Table 10-2, Col. 9, the two lines for t = 6 h and
Mediante el uso de la Ec. 10-4, la constante de almacenamiento del reservorio lineal se puede calcular
directamente de la cola de un hidrograma medido.
Para ilustrar el procedimiento, en la Tabla 10-2, Col. 9, las dos líneas de t = 6 h
y
The average outflow (Col. 9) is: (46.19 + 27.72)/2 = 36.955 m3/s. The rate of change of outflow is: (27.72 - 46.19)/(1 h) = -18.47 (m3/s)/h. Therefore, the storage constant (Eq. 10-4) is:
K =
El flujo de salida promedio (Col. 9) es: (46.19 + 27.72) / 2 = 36.955 m3/s. La velocidad de cambio del flujo de salida es: (27.72 - 46.19) / (1 h) = -18.47 (m 3/s)/h. Por lo tanto, la constante de almacenamiento (Ec. 10-4) es:
K =
Likewise, between t = 7 h and t = 8 h:
K = - [(27.72 + 16.64) / 2] / [(16.64 - 27.72) / (1)] = 2 h
Del mismo modo, entre los t = 7 h y t = 8 h:
K = - [(27,72 + 16,64) / 2] / [(16,64 - 27,72) / (1)] = 2 h
In other words, Eq. 10-4 applies at the tail of the outflow hydrograph, after the translated-only (inflow) hydrograph has receded back to zero. When using the Clark (or time-area) method, the time base of the translated-only hydrograph is equal to the sum of concentration time plus the unit hydrograph (or effective storm) duration (See Eq. 10-1).
En otras palabras, la Ec. 10-4 se aplica a la cola del hidrograma de salida, después del hidrograma trasladado solamente (flujo de entrada) hidrograma ha retrocedido de nuevo a cero. Cuando se utiliza el Clark (o tiempo-área) método, la base de tiempo del hidrograma trasladado solamente es igual a la suma del tiempo de concentración más la duración del hidrograma unitario (o tormenta efectiva) (Véase la Ec. 10-1).
With the help of regional analysis (Chapter 7), the Clark parameters (time of concentration and linear reservoir storage constant) can be estimated based on catchment characteristics. This effectively qualifies the Clark unit hydrograph as a synthetic unit hydrograph. The Eaton [4], O'Kelly [11], and Cordery [3] models are examples of this approach. Singh [18] has a review of Clark synthetic unit hydrograph parameters.
Con la ayuda del análisis regional (Capítulo 7), los parámetros de Clark (tiempo de concentración y constante de almacenamiento del reservorio lineal) se puede estimar basado en las características de la cuenca. Esto califica efectivamente el hidrograma unitario de Clark como un hidrograma unitario sintético. Los modelos de Eaton [4], O'Kelly [11], y Cordery [3] son ejemplos de este enfoque. Singh [18] tiene una opinión de los parámetros del hidrograma unitario sintético de Clark. ***********************
10.3 LA CASCADA DE RESERVORIOS LINEARES
|
|
As seen in Section 8.2, a linear reservoir has a diffusion effect on the inflow hydrograph. If an inflow hydrograph is routed through a linear reservoir, the outflow hydrograph has a reduced peak and an increased time base. This increase in time base causes a difference in the relative timing of inflow and outflow hydrographs, referred to as the lag. The amount of diffusion (and associated lag) is a function of the ratio Δt/K, a larger diffusion effect corresponding to smaller values of Δt/K.
Como se ha visto en la Sección 8.2, un reservorio lineal tiene un efecto de difusión en el hidrograma de entrada. Si un hidrograma de entrada se enruta a través de un reservorio lineal, el hidrograma de salida tiene un pico reducido y un aumento en la base de tiempo. Este aumento en la base de tiempo provoca una diferencia en el tiempo relativo de los hidrogramas de entrada y salida, referido como el retraso. La cantidad de difusión (y el retardo asociado) es una función de la relación Δt/K, un efecto de difusión más largo correspondiente a valores más pequeños de Δt/K.
The cascade of linear reservoirs is a widely used method of hydrologic catchment routing.
As its name implies, the method is based on the connection of several linear reservoirs in series.
For N such reservoirs, the outflow from the first would be taken as inflow to the second, the outflow from the second as inflow to the third, and so on, until the outflow from the (N - 1)th reservoir,
is taken as inflow to the
La cascada de reservorios lineales es un método ampliamente utilizado de enrutamiento de
captación hidrológica.
Como su nombre implica, el método se basa en la conexión de varios reservorios
lineales en serie.
Para tales reservorios N, el flujo de salida de la primera sería tomado como flujo de entrada a la segunda, el flujo de salida desde el segundo como flujo de entrada a la tercera,
y así sucesivamente, hasta que el flujo de salida del (N - 1) ésimo reservorio,
se toma como flujo de entrada a la
Each reservoir in the series provides a certain amount of diffusion and associated lag. For a given set of parameters Δt/K and N, the outflow from the last reservoir is a function of the inflow to the first reservoir. In this way, a one-parameter linear reservoir method (Δt/K) is extended to a two-parameter catchment routing method. Moreover, the basic routing formula (Eq. 8-15) and routing coefficients (Eqs. 8-16 to 8-18) remain essentially the same.
Cada reservorio en la serie proporciona una cierta cantidad de difusión y de retardo asociado. Para un conjunto dado de parámetros Δt/K and N, la salida del flujo del último reservorio es una función del flujo de entrada para el primer reservorio. De esta manera, un método de reservorio lineal de un parámetro (Δt/K) se extiende a un método de tránsito de cuencas de dos parámetros. Por otra parte, la fórmula de enrutamiento básico (Ec. 8-15) y los coeficientes de enrutamiento (Ecs. 8-16 a 8-18) siguen siendo esencialmente los mismos.
The addition of the second parameter (N) provides considerable flexibility in simulating a wide range of diffusion and associated lag effects. However, the conceptual basis of the method restricts its general use, since no direct relation between either of the parameters to the physical problem can be readily envisaged. Notwithstanding this apparent limitation, the method has been widely used in catchment simulation, primarily in applications involving large gaged river basins. Rainfall-runoff data can be used to calibrate the method, i.e., to determine a set of parameters Δt/K and N that produces the best fit to the measured data.
La adición del segundo parámetro (N) proporciona una flexibilidad considerable en la simulación de una amplia gama de difusión y los efectos de retardo asociados. Sin embargo, la base conceptual del método restringe su uso general, ya que hay una relación directa entre cualquiera de los parámetros para el problema físico se puede prever fácilmente. A pesar de esta aparente limitación, el método ha sido ampliamente utilizado en la simulación de captación, sobre todo en aplicaciones que implican las grandes cuencas fluviales amordazada. Los datos de lluvia-escorrentía se pueden utilizar para calibrar el método, es decir, para determinar un conjunto de parámetros Δt/K y N que produce el mejor ajuste a los datos medidos.
The analytical version of the cascade of linear reservoirs is referred to as the Nash model [10]. The numerical version is featured in several hydrologic simulation models developed in the United States and other countries. Notable among them is the SSARR model (Chapter 13), which uses it in its watershed, stream channel routing, and baseflow modules [19]. To derive the routing equation for the method of cascade of linear reservoirs, Eq. 8-15 is reproduced here in a slightly different form:
La versión analítica de la cascada de reservorios lineales se conoce como el modelo de Nash [10]. La versión numérica se ofrece en varios modelos de simulación hidrológica desarrollados en los Estados Unidos y otros países. Notable entre ellos es el modelo SSARR (Capítulo 13), que utiliza en su cuenca, enrutamiento del canal del arroyo, y los módulos del flujo de base [19]. Para derivar la ecuación de enrutamiento para el método de cascada de depósitos lineales, la ecuación. 8-15 se reproduce aquí en una forma ligeramente diferente:
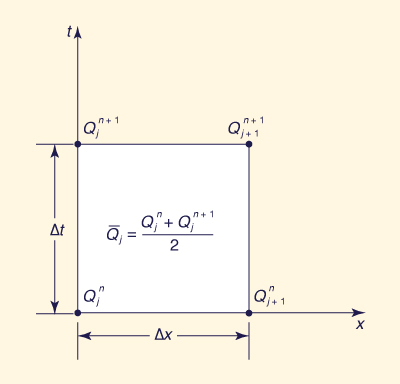
| Q j+1 n+1 = C0 Q j n+1 + C1 Q j n + C2 Q j+1 n | (10-5) |
in which Q represents discharge, whether inflow or outflow and j and n are space and time indexes, respectively (Fig. 10-4).
en la que Q representa la descarga, ya sea fujo de entrada o de salida y j y n son los índices de espacio y tiempo, respectivamente (Fig. 10-4).
Figure 10-4 Space-time discretization in the method of cascade of linear reservoirs. / Figura 10-4 La discretización de espascio-tiempo en el método de cascada de reservorios lineales. |
As with Eq. 8-15, the routing coefficients C0, C1 and C2
are a function of the dimensionless ratio
Al igual que con la Ec. 8-15, los coeficientes de enrutamiento
C0, C1 and C2
son una función de la relación adimensional
|
C C0 = _______ 2 + C | (10-6) |
| C1 = C0 | (10-7) |
|
2 - C C2 = _______ 2 + C | (10-8) |
For application to catchment routing, it is convenient to define the average inflow as follows:
Para la aplicación de tránsito de cuencas, es conveniente definir la media del flujo de entrada de la siguiente manera:
|
Q j n + Q j n+1 Q̄ j = __________________ 2 | (10-9) |
Substituting Eq. 10-6 to 10-9 into Eq. 10-5 gives the following:
Sustituyendo la Ec. 10-6 a 10-9 en la Ec. 10-5 nos da la siguiente:
| Q j+1n+1 = 2 C1 Q̄ j + C2 Q j+1n | (10-10) |
or, alternatively, through algebraic manipulation:
o, alternativamente, a través de la manipulación algebraica:
|
2 C Q j+1n+1 = _________ [ Q̄ j - Q j+1n ] + Q j+1n 2 + C | (10-11) |
Equation 10-11 is the routing equation of the SSARR model [20]. Equations 10-10 and 10-11 are in a form convenient for catchment routing because the inflow is usually a rainfall hyetograph, that is, a constant average value per time interval.
La ecuación 10-11 es la ecuación de enrutamiento del modelo SSARR [20]. Las ecuaciones 10-10 y 10-11 están en una forma conveniente para el enrutamiento de captación debido a que el flujo de entrada es por lo general un hyetograma de precipitaciones, es decir, un valor medio constante por intervalo de tiempo.
Smaller values of C lead to greater amounts of runoff diffusion.
For values of C > 2, the behavior of Eq. 10-10 (or Eq. 10-11) is highly dependent on the type of input.
For instance, in the case of a unit impulse (rainfall duration equal to the time interval), Eq. 10-10
Los valores más bajos de C conducen a una mayor cantidad de difusión de la escorrentía.
Para valores de C > 2, el comportamiento de la Ec. 10-10 (o la Ec. 10-11) es altamente dependiente del tipo de entrada.
Por ejemplo, en el caso de un impulso unitario (la duración de precipitaciones igual al intervalo
de tiempo), la Ec 10-10
The method of cascade of linear reservoirs is illustrated by the following example.
El método de la cascada de reservorios lineales se ilustra con el siguiente ejemplo.
Example 10-3.
Use the method of cascade of linear reservoirs to route the following effective storm hyetograph for a 1000-km2 basin.
Use N = 3, Δt = 6 h and K = 12 h.
Utilizar el método de cascada de los reservorios lineales para enrutar el siguiente hyetograma de tormenta
efectiva para una cuenca de 1000-km2. Usar N = 3, Δt = 6 h and K = 12 h.
The Courant number is C = Δt/K = 6/12 = 1/2, which results in 2C1 = 2/5 and C2 = 3/5.
The computations are shown in Table 10-3.
El número de Courant es C = Δt/K = 6/12 = 1/2, lo que resulta en
2C1 = 2/5 y C2 = 3/5. Los cálculos se muestran en la Tabla 10-3.
Column 1 shows time in hours.
Columna 1 muestra el tiempo en horas.
Column 2 shows the inflow to the first reservoir (in km2-cm/h) calculated by multiplying each one of
the effective rainfall intensities (0.2, 1.0, 0.8, and 0.4 cm/h) times the basin area (1000 km2).
La columna 2 muestra el flujo de entrada al primer reservorio
(en km2-cm/h) calculado multiplicando cada una de las intensidades
de precipitación efectiva (0,2, 1,0, 0,8, y 0,4 cm / h) por el área de la cuenca (1000 km2).
Column 3 is the outflow from the first reservoir.
Columna 3 es el flujo de salida desde el primer reservorio.
Columns 4 and 5 are the inflow and outflow for the second reservoir.
Columnas 4 y 5 son la entrada y salida de flujo para el
segundo reservorio.
Columns 6 and 7 are the inflow and outflow for the third reservoir.
Columnas 6 y 7 son la entrada y salida de flujo para el tercer
reservorio.
Column 8 is the result of the routing, i.e., the outflow from the third reservoir, in m3/s.
Columna 8 es el resultado de la ruta, es decir, el flujo de salida desde el tercer depósito, en m3 / s.
To illustrate the calculations for the first reservoir, following Eq. 10-10, 2/5 of the average inflow for the first time interval [(2/5) × 200 km2-cm/h] plus 3/5 of the outflow at time t = 0 h [(3/5) × 0 km2-cm/h] is equal to the outflow at 6 h: 80 km2cm/h.
Likewise, 2/5 of the average inflow for the second time interval [(2/5) × 1000 km2-cm/hr] plus 3/5 of the outflow at time t = 6 h [(3/5) × 80 km2-cm/h] is equal to the outflow at 12 h: 448 km2-cm/ h, and so on.
Para ilustrar los cálculos para el primer reservorio, siguiendo la Ec. 10-10, 2/5
del flujo de entrada promedio para el primer intervalo de tiempo
[(2/5) × 200 km2-cm/h] más 3/5 del flujo de salida en el tiempo
t = 0 h [(3/5) × 0 km2-cm/h] es igual al flujo de salida a las 6 h:
80 km2cm/h.
Del mismo modo, 2/5 del flujo de entrada promedio para el segundo intervalo de tiempo [(2/5)
× 1000 km2-cm/hr] más 3/5 del flujo de salida en el tiempo t = 6 h
[(3/5) × 80 km2-cm/h] es igual al flujo de salida a las 12 h:
448 km2-cm/ h, y así sucesivamente.
The (average) inflow to the second reservoir (Col. 4) is the average outflow from the first reservoir (Col. 3).
For instance, for the first time interval, 40 km2-cm/h is the average of 0 and 80 km2-cm/h.
El flujo de entrada (promedio) para el segundo reservorio (Col. 4) es el flujo de salida promedio desde el primer
reservorio (Col. 3). Por ejemplo, para el primer intervalo de tiempo, 40 km2-cm/h es
el promedio de 0 y 80 km2-cm/h.
The calculations proceed in a recursive fashion until the routing through the three linear reservoirs has been completed.
Note that the sum of Cols. 3, 5 and 7 is approximately the same: 2400 km2-cm/hr.
Since the time interval is 6 h, this is equivalent to 2400 × 6/1000 = 14.4 cm of effective rainfall depth uniformly distributed over 1000 km2 of basin area.
Los cálculos se realizan de forma recursiva hasta que se haya completado el recorrido a través
de los tres reservorios lineales. Tenga en cuenta que la suma de las Cols. 3, 5 y 7 es aproximadamente la misma:
2400 km2-cm/hr. Dado que el intervalo de tiempo es de 6 h, esto es equivalente a
2400 × 6/1000 = 14.4 cm de profundidad de precipitación efectiva uniformemente distribuida sobre
1000 km2 de área de la cuenca.
Note that the peak outflow from the first reservoir is 588.8 km2-cm/h, and it occurs at 18 h; the peak outflow from the second reservoir is 396.03 km2-cm/h, occurring at 30 h; and the peak outflow from the third reservoir is
308.61 km2-cm/h, occurring at 36 h.
This shows that the effect of the cascade is to produce a certain amount of runoff diffusion at every step, with a corresponding increase in the lag of catchment response.
Nótese que el flujo de salida pico desde el primer reservorio es
588.8 km2-cm/h, y se produce a las 18 h; el flujo de salida pico desde el segundo reservorio es
396.03 km2-cm/h, que se producen a 30 h; y el flujo de salida pico desde el tercer reservorio es
308.61 km2-cm/h, que se producen en 36 h.
Esto muestra que el efecto de la cascada es producir una cierta cantidad de difusión de escorrentía
a cada paso, con el correspondiente aumento en el retraso de la respuesta de captación.
ONLINE CALCULATION.
Using ONLINE ROUTING08, the
result is esentially the same as that of Col. 8, Table 10-3.
CÁLCULO EN LÍNEA.
Usando ROUTING08 EN LÍNEA,
el resultado es esencialmente el mismo como el de la Col. 8, Tabla 10-3.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The cascade of linear reservoirs provides a convenient mechanism for simulating a wide range of catchment routing problems. Furthermore, the method can be applied to each runoff component (surface runoff, subsurface runoff, and baseflow) separately, and the catchment response can be taken as the sum of the responses of the individual components.
La cascada de los reservorios lineales proporciona un mecanismo conveniente para simular una amplia gama de problemas de tránsito de cuencas. Además, el método puede aplicarse a cada componente de escorrentía (escorrentía superficial, la escorrentía subsuperficial, y el flujo de base) por separado, y la respuesta de captación se puede tomar como la suma de las respuestas de los componentes individuales.
For instance, assume that a certain basin has 10 cm of runoff, of which 7 cm are surface runoff, 2 cm are subsurface runoff, and 1 cm is baseflow. Since surface runoff is the less diffused process, it can be simulated with a high Courant number, say C = 1, and a small number of reservoirs, say N = 3. Subsurface runoff is much more diffused than surface runoff; therefore, it can be simulated with C = 0.4 and N = 5. Baseflow, being very diffused, can be simulated with C = 0.1 and N = 7. In practice, the parameters C and N are determined by extensive calibration. In this sense, the cascade of linear reservoirs remains essentially a conceptual model [17].
Por ejemplo, supongamos que una determinada cuenca tiene 10 cm de escorrentía, de las cuales 7 cm son la escorrentía superficial, 2 cm son escorrentía subsuperficial, y 1 cm es el caudal base. Desde la escorrentía superficial es el proceso menos difusa, puede ser simulado con un alto número de Courant, decir C = 1, y un pequeño número de reservorios, por ejemplo N = 3. Escorrentía subsuperficial es mucho más difusa que la escorrentía superficial; por lo tanto, se puede simular con C = 0.4 y N = 5. El flujo base, siendo muy difusa, puede ser simulado con C = 0.1 y N = 7. En la práctica, los parámetros C y N se determinan por calibración extensiva. En este sentido, la cascada de reservorios lineales sigue siendo esencialmente un modelo conceptual [17].
10.4 ONDAS CINEMÁTICAS
|
|
Hydraulic catchment routing using kinematic waves was introduced by Wooding in 1965 [21, 22, 23]. Since then, the kinematic wave approach has been widely used in deterministic catchment modeling. The approach can be either lumped or distributed, depending on whether the parameters are kept constant or allowed to vary in space. Analytical solutions are suited to lumped modeling, whereas numerical solutions lend themselves to distributed modeling.
El tránsito de cuencas hidráulica usando las ondas cinemáticas fue introducido por Wooding en 1965 [21, 22, 23]. Desde entonces, el enfoque de onda cinemática ha sido ampliamente utilizado en el modelado de captación determinista. El enfoque puede ser ya sea agrupado o distribuido, dependiendo de si los parámetros se mantienen constantes o se les permite variar en el espacio. Las soluciones analíticas son adecuados para el modelado agrupado, mientras que las soluciones numéricas se prestan a la modelación distribuida.
Wooding used an open-book geometric configuration (Fig. 4-15) to represent the catchment-stream problem physically. As its name implies, an open-book configuration consists of two rectangular catchments separated by a stream and draining laterally into it; in turn the streamflow drains out of the catchment outlet. Wooding used analytical solutions of kinematic waves and the method of characteristics to formulate his method. Since diffusion is absent from these solutions, the method is strictly applicable only to kinematic waves. Criteria for the applicability of kinematic waves have been developed by Woolhiser and Liggett [24] (Eq. 4-55) for overland flow, and by Ponce et al. [12] for stream channel flow (Eq. 9-44).
Wooding utiliza una configuración geométrica a libro abierto (Fig. 4-15) para representar el problema de captación de corriente físicamente. Como su nombre lo indica, una configuración a libro abierto se compone de dos cuencas rectangulares separadas por un arroyo y drenaje lateralmente en ella; a su vez, los desagües de caudal fuera de la salida de la cuenca. Wooding utiliza soluciones analíticas de las ondas cinemáticas y el método de las características de formular su método. Dado que la difusión está ausente de estas soluciones, el método está estrictamente aplicable solamente a las ondas cinemáticas. Criterios para la aplicabilidad de las ondas cinemáticas han sido desarrollados por Woolhiser y Liggett [24] (Ec. 4-55) para el flujo superficial, y por Ponce et al. [12] para el flujo del canal del arroyo (Ec. 9-44).
Kinematic catchment routing models can be approached in a variety of ways. Methods can be either (1) analytical or numerical, (2) lumped or distributed, (3) linear or nonlinear, or (4) single plane, two-plane, or a cascade of planes [7, 8]. Analytical models take advantage of the nondiffusive properties of kinematic waves, whereas numerical models are usually based on the method of finite differences. Linear models assume a constant wave celerity, but nonlinear models relax this restriction. The feature of variable wave celerity often renders the nonlinear models impractical because of wave steepening and associated kinematic shock development [8, 13]. Single- and two-plane models are used in hydrologic engineering practice [7].
Los modelos de tránsito de cuencas cinemáticos pueden abordarse en una variedad de formas. Los métodos pueden ser (1) analítica o numérica, (2) agrupado o distribuido, (3) lineal o no lineal, o (4) plano único, de dos planos, o una cascada de planos [7, 8]. Los modelos analíticos toman ventaja de las propiedades no difusivas de las ondas cinemáticas, mientras que los modelos numéricos se basan generalmente en el método de las diferencias finitas. Los modelos lineales asumen una celeridad de la onda constante, pero los modelos no lineales relajan esta restricción. La característica de la celeridad de onda variable menudo hace que los modelos no lineales impracticables debido al empinamiento de onda y asociada al desarrollo de choque cinemático [8, 13]. Los modelos de uno y de dos planos se utilizan en la práctica de la ingeniería hidrológica [7].
The application of kinematic wave modeling to catchment routing is illustrated here with an example of a two-plane finite difference numerical model. The model could be either lumped or distributed, depending on whether the inputs and parameters are allowed to vary in space or not. For simplicity, this example considers constant input (i.e., constant effective rainfall) and constant parameters (i.e., a linear mode of computation). In practice, a computer-aided solution may relax this restriction.
La aplicación del modelado de la onda cinemática de tránsito de cuencas se ilustra aquí con un ejemplo de un modelo numérico de diferencias finitas en dos planos. El modelo podría ser ya sea agrupado o distribuido, dependiendo de si las entradas y parámetros pueden variar en el espacio o no. Para simplificar, este ejemplo considera una entrada constante (es decir, la precipitación efectiva constante) y parámetros constantes (es decir, un modo lineal de cálculo). En la práctica, una solución asistido por la computadora puede relajar esta restricción.
Two-Plane Linear Kinematic Catchment Routing Model / Modelo de tránsito de cuencas Cinemático Lineal de Dos Planos
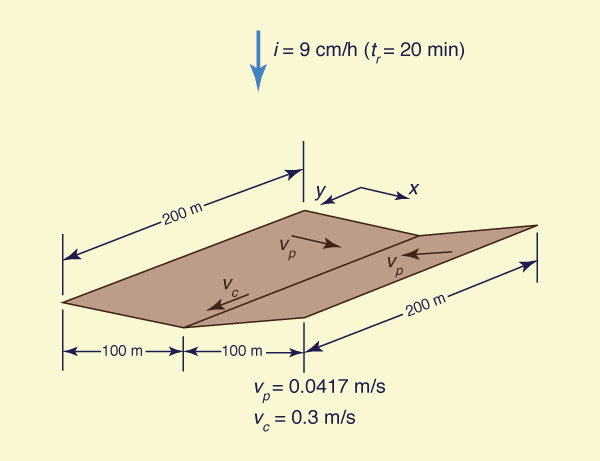
Assume a catchment configured as two rectangular planes adjacent to each other, draining laterally into a stream channel located between them. Each of the planes is 100 m long by 200 m wide, and the channel is 200 m long (Fig. 10-5). The bottom friction in the planes and channel is such that the average velocity in the planes is 0.0417 m/s and the average velocity in the channel is 0.3 m/s. It is desired to obtain the hydrograph at the catchment outlet resulting from an effective rainfall of 9 cm/h lasting 20 min.
Supongamos una cuenca configurada como dos planos rectangulares adyacentes entre sí, que drenan lateralmente en un canal de flujo situado entre ellos. Cada uno de los planos es de 100 m de largo por 200 m de ancho, y el canal es de 200 m de largo (Fig. 10-5). La fricción de fondo en los planos y el canal es tal que la velocidad media en los planos es 0.0417 m/s y la velocidad media en el canal es de 0.3 m/s. Se desea obtener el hidrograma en la salida de captación resultante de una precipitación efectiva de 9 cm/h de duración de 20 min.
Figure 10-5 Two-plane linear kinematic catchment routing model. / Modelo de tránsito de cuencas Cinemático Lineal de Dos Planos |
Calculation of flow parameters. Since the model is linear, it is first necessary to calculate the flow parameters on which to base the calculation of the routing parameters and coefficients.
Cálculo de parámetros de flujo. Puesto que el modelo es lineal, primero es necesario calcular los parámetros de flujo en la cual basar del cálculo de los parámetros de encaminamiento y coeficientes.
The flow per unit width in the midlength of each plane is equal to the effective rainfall intensity times the contributing area (50 m × 1 m):
El flujo por unidad de anchura en la mitad de su longitud de cada plano es igual a la intensidad de precipitación efectiva por el área que contribuye (50 m × 1 m):
|
9 cm/h × 50 m × 0.01 m/cm qp = ________________________________ = 0.00125 m2/s 3600 s/h | (10-12) |
Since the average velocity in the planes is vp = 0.0417 m/s, the average flow depth in the planes is:
Puesto que la velocidad media en los planos es vp = 0.0417 m/s, la profundidad de flujo promedio en los planos es:
Laminar flow in the planes is assumed, with discharge-depth rating exponent βp = 3. Therefore, the wave celerity in the planes is:
El flujo laminar en los planos es asumido, con el exponente de valoración de la profundidad de descarga βp = 3. Por lo tanto, la celeridad de la onda en los planos es:
cp = βp vp = 3 × 0.0417 = 0.125 m/s
The flow in the midlength of the channel is equal to the effective rainfall intensity times the contributing area (2 planes × 100 m × 100 m):
El flujo en la longitud media del canal es igual a la intensidad de precipitación efectiva por el área que contribuye (2 planes × 100 m × 100 m):
|
9 cm/h × 2 × 100 m × 100 m × 0.01 m/cm Qc = ____________________________________________ = 0.5 m3/s 3600 s/h | (10-13) |
Assume a channel top width Tc = 5 m. Therefore, the flow per unit width in the channel is:
Asumir una anchura superior del canal Tc = 5 m. Por lo tanto, el flujo por unidad de anchura en el canal es:
qc =
Since the average velocity in the channel is vc = 0.3 m/s, the average flow depth in the channel (at midlength) is:
Puesto que la velocidad promedio en el canal es vc = 0.3 m/s, la profundidad del flujo promedio en el canal (en la longitud media) es:
dc =
A wide channel and turbulent Manning friction is assumed, with discharge-area rating exponent βc = 1.67. Therefore, the wave celerity in the channel is:
Se supone un canal amplio y una fricción de Manning turbulento, con el exponente de valoración del área de descarga calificación de descarga βc = 1.67. Por lo tanto, la celeridad de la onda en el canal es:
cc = βc vc = 1.67 × 0.3 = 0.5 m/s
The time of conncentration equal to the travel time in the planes plus the travel time in the channel.
The travel time in the planes is: (100 m)/(0.125 m/s) = 800 s.
The travel time in the channel is:
El tiempo de concentración igual al tiempo de viaje en los planos más el tiempo de viaje en el canal.
El tiempo de viaje en los planos es: (100 m) / (0.125 m / s) = 800 s.
El tiempo de viaje en el canal es:
The maximum possible (i.e., equilibrium) peak flow is equal to the product of rainfall intensity and catchment area:
El flujo pico máximo posible (es decir, el equilibrio) es igual al producto de la intensidad de precipitación y el área de captación:
|
9 cm/h × 2 × 100 m × 200 m × 0.01 m/cm Qc = ____________________________________________ = 1 m3/s 3600 s/h | (10-14) |
The total volume of runoff is:
El volumen total de escorrentía es:
|
9 cm/h × 20 min × 2 × 100 m × 200 m Qc = _________________________________________ = 1200 m3 100 cm/m × 60 min/h | (10-15) |
Selection of discrete intervals. For simplicity, a space interval Δx = 100 m is chosen for the planes. This amounts to one spatial increment in the planes. In an actual application using a computer, a smaller value of Δx would be indicated. The time interval is chosen as Δt = 10 min (the rainfall duration is tr = 20 min). This leads to a Courant number in the planes:
La selección de intervalos discretos. Por simplicidad, se elige un intervalo de espacio Δx = 100 m para los planos. Esto equivale a un incremento espacial en los planos. En una aplicación real usando una computadora, un valor menor de Δx sería indicado. El intervalo de tiempo es elegido como Δt = 10 min (la duración de precipitación es tr = 20 min). Esto conduce a un número de Courant en los planos:
Cp = cp (Δt /Δx) = 0.75
In the case of the channel, a space interval
Cp = cp (Δt /Δx) = 0.75
En el caso del canal, un intervalo de espacio
Cc = cc (Δt /Δx) = 1.5
Selection of routing scheme. There are many possible choices for routing scheme. Either first- or second-order schemes may be used (Section 9.2). In practice, first-order schemes are preferred because they are more stable than second-order schemes (compare the results of a first order scheme, Table 9-5, with those of a second order scheme, Table 9-4).
Selección del esquema de enrutamiento. Hay muchas opciones posibles para el sistema de enrutamiento. Cualquiera de los esquemas de primer o segundo orden pueden utilizarse (Sección 9.2). En la práctica, los esquemas de primer orden se prefieren porque ellos son más estables que los esquemas de segundo orden (comparar los resultados de un sistema de primer orden, la Tabla 9-5, con los de un sistema de segundo orden, Tabla 9-4).
Two first-order schemes are chosen here: (1) Scheme I, forward-in-time, backward-in-space, stable for Courant numbers C ≤ 1 (similar to the convex method, see Example 9-5), and (2) Scheme II, forward-in-space, backward-in-time, stable for Courant numbers C ≥ 1 (exact opposite of the convex method). The use of these two schemes guarantees that the solution will remain stable because scheme I is used for Courant numbers C ≤ 1, whereas scheme II is used for Courant numbers C > 1 [7]. In the present application, scheme I is used for routing in the planes (Cp = 0.75), and scheme II is used for routing in the channel (Cc = 1.5).
Dos esquemas de primer orden se eligen aquí: (1) Esquema I, hacia adelante en el tiempo, hacia atrás en el espacio, y estable para los números de Courant C ≤ 1 (similar al método convexo, véase el Ejemplo 9-5), y ( 2) Esquema II, hacia adelante en el espacio, hacia atrás en el tiempo, estable para los números de Courant C ≥ 1 (exactamente lo contrario del método convexo). El uso de estos dos esquemas garantiza que la solución permanecerá estable porque el esquema I se utiliza para los números de Courant C ≤ 1, mientras que el esquema II se utiliza para los números de Courant C > 1 [7]. En la presente aplicación, el esquema I se utiliza para el enrutamiento en los planos (Cp = 0.75), y el esquema II se utiliza para el enrutamiento en el canal (Cc = 1.5).
Lateral inflows are an integral part of catchment routing. For routing in the planes, lateral inflow is the effective rainfall; for channel routing, lateral inflow is the lateral contribution from the planes. Therefore, it is necessary to discretize the kinematic wave equation with lateral inflow, Eq. 9-43.
La entrada de flujos laterales son una parte integral de tránsito de cuencas. Para el enrutamiento en los planos, la entrada de flujo lateral es la precipitación efectiva; para el enrutamiento del canal, la entrada lateral es la contribución lateral de los planos. Por lo tanto, es necesario discretizar la ecuación de onda cinemática con la entrada de flujo lateral, Ec. 9-43.
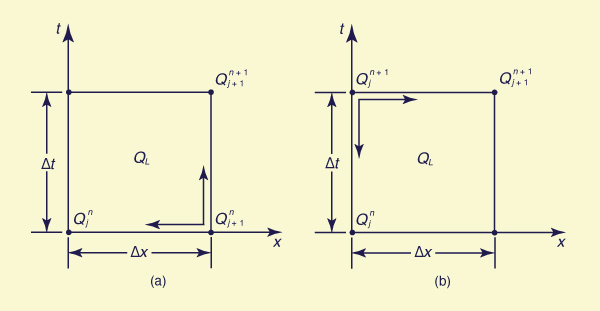
The discretization of Eq. 9-43 in a forward-in-time, backward-in-space linear scheme, as shown in Fig. 10-6 (a), leads to:
La discretización de la ecuación. 9-43 en un esquema hacia delante en el tiempo, lineal hacia atrás en el espacio, como se muestra en la Fig. 6.10 (a), conduce a:
| Q j+1 n+1 = C1 Q j n + C2 Q j+1n + C3 QL | (10-16) |
en la cual
| C1 = C | (10-16a) |
| C2 = 1 - C | (10-16b) |
| C3 = C | (10-16c) |
with the Courant number C = βv Δt /Δs, with Δs either Δx (planes) or Δy (channel). The term QL is the lateral inflow in cubic meters per second. For routing in the planes, the lateral inflow is equal to the effective rainfall (centimeters per hour) times the applicable area (square meters). For channel routing, the lateral inflow is the average distributed lateral inflow (cubic meters per second per meter) multiplied by the channel length (meters).
con el número de Courant C = βv Δt /Δs, con Δs ya sea Δx (planos) o Δy (canal). El término QL es el flujo de entrada lateral en metros cúbicos por segundo. Para el enrutamiento en los planos, la entrada de flujo lateral es igual a la precipitación efectiva (centímetros por hora) por el área de aplicación (metros cuadrados). Para enrutamiento del canal, el flujo de entrada lateral es el promedio de la entrada de flujo lateral distribuida (metros cúbicos por segundo por metro) multiplicado por la longitud del canal (metros).
Figure 10-6 Space-time discretization of first-order schemes of kinematic wave equation with lateral inflow: |
The discretization of Eq. 9-43 in a forward-in-space, backward-in-time linear scheme, as shown in Fig. 10-6 (b), leads to:
La discretización de la Ec. 9-43 en un esquema hacia delante en el espacio, lineal hacia atrás en el tiempo, como se muestra en la Fig. 10.6 (b), conduce a:
| Q j+1 n+1 = C0 Q j n+1 + C1 Q j n + C3 QL | (10-17) |
en la cual
| C0 = (C - 1) /C | (10-17a) |
| C1 = 1/C | (10-17a) |
| C3 = 1 | (10-17a) |
The catchment routing is shown in Table 10-4.
El tránsito de cuencas se muestra en la Tabla 10-4.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Explicación de la Tabla 10-4.
Column 1 shows time in minutes,
Columna 1 muestra el tiempo en minutos,
Cols. 2-4 show the plane routing, and Cols. 5-7 show the channel routing.
Cols. 2-4 muestran el enrutamiento del plano, y Cols. 5-7 muestran la ruta del canal.
Column 2 shows the lateral inflow to each plane, calculated as follows:
La columna 2 muestra el flujo de entrada lateral a cada plano, calculado como sigue:
9 cm/h × 100 m × 200 m × 0.01 m/cm
QLp = _________________________________________ = 0.5 m3/s
3600 s/h(10-18) Note that the lateral inflow is an average value for a time interval, and it lasts 20 min (i.e., the effective rainfall duration).
Nótese que el flujo de entrada lateral es un valor promedio para un intervalo de tiempo, y dura 20 min (es decir, la duración de precipitaciones efectiva).
Column 3 shows the upstream inflow to the plane, that is, zero (this example does not consider upstream inflow to the planes).
La Columna 3 muestra el flujo de entrada de aguas arriba al plano, es decir, cero (este ejemplo no tiene en cuenta el flujo de entrada aguas arriba a los planos).
Column 4 is obtained by routing with Eq. 10-16, with Courant number in the planes
Cp = 0.75. Column 4 is the outflow hydrograph from each plane. The first value of Col. 4 (for t = 0) is: 0; the second value is: (0.75 × 0) + (0.25 × 0) + (0.75 × 0.5) = 0.3750; the third value is: (0.75 × 0) + (0.25 × 0.3750) + (0.75 × 0.5) = 0.4687; and so on.La Columna 4 se obtiene por enrutamiento con la Ec. 10-16, con el número de Courant en los planos
Cp = 0.75. La columna 4 es el hidrograma del flujo de salida de cada plano. El primer valor de la Col. 4 (para t = 0) es: 0; el segundo valor es: (0.75 × 0) + (0.25 × 0) + (0.75 × 0.5) = 0.3750; el tercer valor es: (0.75 × 0) + (0.25 × 0.3750) + (0.75 × 0.5) = 0.4687; y así sucesivamente.The sum of Col. 2 is 1.0; likewise, the sum of Col. 4 is 0.9999, which confirms that the volume under the outflow hydrograph from each plane is 1 m3/s × 10 min × 60 s/min = 600 m3.
La suma de la Col. 2 es de 1.0; del mismo modo, la suma de Col. 4 es 0.9999, lo que confirma que el volumen bajo el hidrograma de flujo de salida de cada plano es 1 m3/s × 10 min × 60 s/min = 600 m3.
Column 5 shows the average lateral inflow to the channel, obtained by multiplying by 2 the average lateral inflow from each plane (Col. 4) (to account for two planes of the same dimensions). The first value of Col. 5 is: [(0 + 0.3750)/2] × 2 = 0.3750; the second value is: [(0.3750 + 0.4687)/2] × 2 = 0.8437; and so on.
La columna 5 muestra el promedio del flujo de entrada lateral al canal, que se obtiene multiplicando por 2 el promedio de la entrada de flujo lateral de cada plano (Col. 4) (para dar cuenta de dos planos de las mismas dimensiones). El primer valor de la Col. 5 es: [(0 + 0.3750)/2] × 2 = 0.3750; el segundo valor es: [(0.3750 + 0.4687)/2] × 2 = 0.8437; y así sucesivamente.
Column 6 is the upstream inflow to the channel, that is, zero (this example does not consider upstream inflow to the channel).
La Columna 6 es la entrada de flujo aguas arriba al canal, es decir, cero (este ejemplo no tiene en cuenta la entrada de flujo aguas arriba en el canal).
Column 7 is obtained by routing with Eq. 10-17, with Courant number in the channel
Cc = 1.5. The first value of Col. 7 (for t = 0) is: 0; the second value is: (0.33 × 0) + (0.67 × 0) + (1.00 × 0.3750) = 0.3750; the third value is: (0.33 × 0) + (0.67 × 0) + (1.00 × 0.8437) = 0.8437; and so on.La Columna 7 se obtiene por enrutamiento con la Ec. 10-17, con número de Courant en el canal
Cc = 1.5. El primer valor de Col. 7 (para t = 0) es: 0; el segundo valor es: (0.33 × 0) + (0.67 × 0) + (1.00 × 0.3750) = 0.3750; el tercer valor es: (0.33 × 0) + (0.67 × 0) + (1.00 × 0.8437) = 0.8437; y así sucesivamente.The sum of Col. 7 is 1.9998, confirming that the total runoff volume is:
La suma de Col. 7 es 1,9998, lo que confirma que el volumen total de escorrentía es:
1.9998 m3/s × 10 min × 60 s/min = 1200 m3.
Column 7 is the outflow hydrograph from the catchment.
La Columna 7 es el hidrograma del flujo de salida de la cuenca.
Assessment of kinematic wave method.
The calculated outflow hydrograph peak is 0.8437 m3/s, and it occurs at 20 min.
This value is less than the maximum peak flow, Eq. 10-14: 1 m3/s.
Since the rainfall duration is equal to the time of concentration this implies that the hydrograph has undergone a certain
amount of runoff diffusion.
This diffusion is really numerical diffusion, due primarily to the coarse grid size and secondarily to the Courant numbers
(of planes and channel) being different
Evaluación del método de onda cinemática.
El pico del hidrograma del flujo de salida calculado es 0.8437 m3/s, y se produce a los 20 min. Este valor es menor que el flujo pico m´ximo, la Ec. 10-14:
1 m3/s. Dado que la duración de precipitaciones es igual al tiempo de concentración esto implica que el hidrograma se ha sometido a una cierta cantidad de difusión
de escorrentía.
Esta difusión es realmente difusión numérica, debido principalmente al tamaño de la malla gruesa
y secundariamente a los números de Courant (de planos y canal) siendo diferente a
To prove this assertion, it is necessary to reduce the grid size and test the convergence of the kinematic wave schemes, Eqs. 10-16 and 10-17. Convergence refers to the ability of the numerical scheme to approach the analytical solution as the grid is refined. Due to the large number of calculations involved, the procedure is better accomplished with the aid of a computer program. Table 10-5 shows the results obtained by successive grid refinement, using program EH1000B.
Para demostrar esta afirmación, es necesario reducir el tamaño de la malla y probar la convergencia de los esquemas de onda cinemática, las Ecs. 10-16 y 10-17. La convergencia se refiere a la capacidad del esquema numérico para acercarse a la solución analítica como la malla se refine. Debido al gran número de cálculos involucrados, el procedimiento es mejor logrado con la ayuda de un programa informático. La Tabla 10-5 muestra los resultados obtenidos por el refinamiento de la rejilla sucesiva, utilizando el programa EH1000B.
| |||||||||||||||||||||||||||||||||||||
It is seen that the results are a function of grid size and that the peak flow value converges to the maximum possible value (1 m3/s) as the grid is refined.
Se ve que los resultados son una función del tamaño de la malla y que el valor de flujol máximo converge al valor máximo posible (1 m3/s) como la malla sea refinada.
It is concluded that a kinematic wave numerical solution for catchment routing is grid dependent. If necessary, numerical diffusion can be eliminated by successive grid refinement (while keeping the Courant number as close to 1 as possible). However, in this case the calculated hydrograph would be translated only, with no diffusion. This may be adequate for catchments with negligible runoff diffusion (e.g., small catchments with slopes on the order of 1% or more), but is generally not adequate for catchments showing substantial amounts of runoff diffusion (e.g., midsize catchments of mild relief). For the latter, the diffusion wave technique may be used as a viable alternative to the kinematic wave.
Se concluye que una solución numérica de onda cinemática para el tránsito de cuencas depende de la malla. Si es necesario, la difusión numérica puede ser eliminado por el refinamiento de la malla sucesiva (mientras se mantiene el número de Courant tan cercano a 1 como sea posible). Sin embargo, en este caso el hidrograma calculado se traduciría solamente, sin difusión. Esto puede ser adecuado para las cuencas con la difusión de escorrentía insignificante (por ejemplo, pequeñas cuencas con pendientes del orden de 1% o más), pero en general no es adecuado para las cuencas que muestran cantidades sustanciales de difusión de escorrentía (por ejemplo, las cuencas de tamaño medio de alivio leve). En este último caso, la técnica de la onda de difusión puede ser utilizado como una alternativa viable a la onda cinemática.
10.5 ONDAS DIFUSIVAS
|
|
Catchment routing with diffusion waves is applicable to cases where both translation and diffusion are important, that is, for routing in midsize catchments where catchment slope is such that the kinematic wave criterion is not satisfied. Although the concept of diffusion waves and catchment routing dates back to the work of Dooge [1], actual numerical applications are relatively more recent [14, 16]. Diffusion wave routing can provide grid-independent results, and is therefore regarded as an improvement over grid-dependent techniques.
La captación de enrutamiento con las ondas de difusión es aplicable a los casos en que tanto la traducción y difusión son importantes, es decir, para el encaminamiento en cuencas medianas donde la pendiente de la cuenca es tal que el criterio de la onda cinemática no está satisfecho. Aunque el concepto de las ondas de difusión y enrutamiento de la cuenca se remonta a la obra de Dooge [1], las aplicaciones numéricas reales son relativamente más recientes [14, 16]. Enrutamiento de onda de difusión puede proporcionar resultados de la malla independiente, y por lo tanto se considera como una mejora sobre las técnicas de malla dependiente.
The diffusion wave catchment routing approach is illustrated here by using the same example as in the previous section. The Muskingum-Cunge method (Chapter 9) is used as the routing scheme of the diffusion wave method [14].
El enfoque de tránsito de cuencas de onda de difusión se ilustra aquí mediante el uso del mismo ejemplo como en la sección anterior El método de Muskingum-Cunge (Capítulo 9) se utiliza como el esquema de enrutamiento del método de la onda de difusión [14].
Two-Plane Linear Diffusion Catchment Routing Model/ Modelo de Enrutamiento de Captación de Difusión Lineal de Dos Planos
This example is similar to that of the previous section. Assume a catchment configured as two rectangular planes adjacent to each other, draining laterally into a stream channel located between them. Each of the planes is 100 m long by 200 m wide, and the channel is 200 m long (Fig. 10-5). The slopes of planes and channel (in the direction of the flow) are Sop = 0.01; and Soc = 0.01, respectively. The bottom friction in the planes and channel is such that the average velocity in the planes is vp = 0.0417 m/s, and the average velocity in the channel is vc = 0.3 m/s. It is desired to calculate the runoff hydrograph at the catchment outlet resulting from an effective rainfall of 9 cm/h lasting 20 min.
Este ejemplo es similar a la de la sección anterior. Supongamos una cuenca configurada como dos planos rectangulares adyacentes entre sí, que drenan lateralmente en un canal de flujo situado entre ellos. Cada uno de los planos es de 100 m de largo por 200 m de ancho, y el canal es de 200 m de largo (Fig. 10-5). Las pendientes de los planos y del canal (en la dirección del flujo) son Sop = 0.01; and Soc = 0.01, respectivamente. La fricción de fondo en los planos y el canal es tal que la velocidad media en los planos es vp = 0.0417 m/s, y la velocidad media en el canal es vc = 0.3 m/s. Se desea calcular el hidrograma de escorrentía en el flujo de salida de la cuenca resultante de una precipitación efectiva de 9 cm/h durando 20 min.
Calculation of flow parameters. Since the model is linear, it is first necessary to calculate the flow parameters on which to base the calculation of the routing parameters and coefficients. As described in the preceding section, the flow per unit width in the mid length of each plane is equal to qp = 0.00125 m2/s. Since the average velocity in the planes is vp = 0.0417 m/s, the average flow depth in the planes is dp = qp/vp = 0.03 m. Laminar flow in the planes is assumed, with a discharge-depth rating exponent βp = 3. Therefore, the wave celerity in the planes is cp = βpvp = 0.125 m/s.
Cálculo de los parámetros de flujo. Puesto que el modelo es lineal, primero es necesario calcular los parámetros de flujo en los cuales basar el cálculo de los parámetros de enrutamiento y coeficientes. Como se describe en la sección anterior, el flujo por unidad de anchura en la longitud media de cada plano es igual a qp = 0.00125 m2/s. Puesto que la velocidad media en los planos es vp = 0.0417 m/s, la profundidad de flujo media en los planos es dp = qp/vp = 0.03 m. Se supone flujo laminar en los planos, con un exponente de valoración de descarga-profundidad βp = 3. Por lo tanto, la celeridad de la onda en los planos es cp = βpvp = 0.125 m/s.
The flow in the midlength of the channel is equal to 0.5 m3/s.
Assume a channel top width
El flujo en la longitud media del canal es igual a 0.5 m3/s.
Asumir una anchura superior del canal
The time of concentration is equal to 1200 s, which is equal to the rainfall duration. The maximum possible peak flow is 1.0 m3/s. The total volume of runoff is 1200 m3.
El tiempo de concentración es igual a 1200 s, lo cual es igual a la duración de precipitaciones. El flujo pico máximo posible es 1.0 m3/s. El volumen total de escorrentía es de 1200 m3.
For simplicity, a space interval of Δx = 100 m is chosen for the planes, and Δy = 200 m for the channel. This amounts to one spatial increment in planes and channel. The time interval is chosen as Δt = 10 minutes. In an actual computer application, a finer grid size would be indicated.
Por simplicidad, un intervalo de espacio de Δx = 100 m es elegido por los planos, y Δy = 200 m para el canal. Esto representa a un incremento espacial en planos y canal. El intervalo de tiempo es elegido como Δt = 10 minutos. En una aplicación de cómputo actual, un tamaño de malla más fina sería indicada.
Selection of routing scheme.
The chosen routing scheme is the Muskingum-Cunge method,
Selección del método de tránsito.
El método de tránsito elegido es el método Muskingum-Cunge,
| Q j+1n+1 = C0 Q j n+1 + C1 Q j n + C2 Q j+1n + C3 QL | (10-19) |
which has the same meaning as Eq. 9-62 with Eqs. 9-74 to 9-76, except for the addition of the lateral inflow term, with routing coefficient [14]:
que tiene el mismo significado que la Ec. 9-62 con Ecs. 9-74 a 9-76, excepto por la adición del término flujo de entrada lateral, con coeficiente de enrutamiento [14]:
|
2 C C3 = _____________ 1 + C + D | (10-20) |
The term QL is the lateral inflow in cubic meters per second. For overland flow routing, the lateral inflow is equal to the effective rainfall (centimeters per hour) times the applicable area (square meters). For channel routing, the lateral inflow is the average distributed lateral inflow (cubic meters per second per meter) multiplied by the channel length (meters).
El término QL es el flujo de entrada lateral en metros cúbicos por segundo. Para el enrutamiento del flujo superficial, el flujo de entrada lateral es igual a la precipitación efectiva (centímetros por hora) por el área aplicable (metros cuadrados). Para el enrutamiento del canal, el flujo de entrada lateral es el promedio del flujo de entrada lateral distribuida (metros cúbicos por segundo por metro) multiplicado por la longitud del canal (metros).
The grid size and physical parameters allow the calculation of the routing parameters. The Courant numbers in the planes and channel (Eq. 9-69) are: Cp = 0.75 and Cc = 1.5, respectively. The cell Reynolds numbers in the planes and channel (Eq. 9-71) are: Dp = 0.01 and Dc = 0.1, respectively.
El tamaño de la malla y los parámetros físicos permiten el cálculo de los parámetros de enrutamiento. Los números de Courant en los planos y canal (Ec. 9-69) son: Cp = 0.75 and Cc = 1.5, respectivamente. Los números de Reynolds de células en los planos y canal (Ec. 9-71) son: Dp = 0.01 y Dc = 0.1, respectivamente.
With Eqs. 9-74 to 9-76 and 10-20, the routing coefficients in the planes are: C0 =
Con las Ecs. 9-74 a 9-76 y 10-20, los coeficientes de enrutamiento en los planos son:
C0 =
The catchment routing is shown in Table 10-6.
El enrutamiento de la cuenca se muestra en la Tabla 10-6.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Explanation of Table 10-6. / Explicación de la Tabla 10-6.
Column 1 shows time in minutes.
La columna 1 muestra el tiempo en minutos.
Columns 2-4 show the plane routing and Cols. 5-7 show the channel routing.
Las columnas 2-4 muestran el enrutamiento de planos y las Cols. 5-7 muestran la ruta del canal.
As in the previous example, the lateral inflow to the plane is 0.5 m3/s (Eq. 10-18).
Como en el ejemplo anterior, el flujo de entrada lateral al plano es de 0.5 0.5 m3/s (Eq. 10-18).
Column 3 shows the upstream inflow to each plane, that is, zero (this example does not consider upstream inflow to the planes).
La Columna 3 muestra el flujo de entrada aguas arriba de cada plano, es decir, cero (este ejemplo no tiene en cuenta el flujo de entrada aguas arriba a los planos).
Column 4 is the outflow from each one of the planes, obtained by routing with
Eq. 10-19. The first value of Col. 4 (for t = 0) is: 0. The second value of Col. 4 is: (- 0.136 × 0) + (0.988 × 0) + (0.148 × 0) + (0.852 × 0.5) = 0.4260. The third value of Col. 4 is: (- 0.136 × 0) + (0.988 × 0) + (0.148 × 0.4260) + (0.852 × 0.5) = 0.4890. The remaining values in Col. 4 are calculated in a similar way.La Columna 4 es el flujo de salida de cada uno de los planos, obtenidos mediante el enrutamiento con la
Ec. 10-19. El primer valor de la Col. 4 (para t = 0) es: 0. El segundo valor de la Col. 4 es: (- 0.136 × 0) + (0.988 × 0) + (0.148 × 0) + (0.852 × 0.5) = 0.4260. El tercer valor de la Col. 4 es: (- 0.136 × 0) + (0.988 × 0) + (0.148 × 0.4260) + (0.852 × 0.5) = 0.4890. Los valores restantes en la Col. 4 se calculan de una manera similar.Column 5 shows the average lateral inflow to the channel, obtained by multipying by 2 the average inflow from each plane (Col. 4) (two planes, each of the same dimensions).
La columna 5 muestra el flujo de entrada lateral promedio al canal, obtenidos multiplicando por 2 el promedio de flujo de entrada de cada plano (Col. 4) (dos planos, cada una de las mismas dimensiones).
Column 6 is the upstream inflow to the channel, that is, zero (this example does not consider upstream inflow to the channel).
La Columna 6 es el flujo de entrada aguas arriba a el canal, es decir, cero (este ejemplo no tiene en cuenta el flujo de entrada aguas arriba a el canal).
Column 7 is the outflow from the catchment, obtained by routing with Eq. 10-19. The first value of Col. 6 (for t = 0) is: 0. The second value of Col. 6 is: (0.231 × 0) + (0.923 × 0) + (- 0.154 × 0) + (1.154 × 0.4260) = 0.4916. The third value of Col. 6 is: (0.231 × 0) + (0.923 × 0) + (- 0.154 × 0.4916) + (1.154 × 0.9150) = 0.9802. The remaining values in Col. 6 are calculated in a similar way.
La Columna 7 es el flujo de salida del área de captación, obtenido mediante el enrutamiento con la Ec. 10-19. El primer valor de la Col. 6 (para t = 0) es: 0. El segundo valor de la Col. 6 es: (0.231 × 0) + (0.923 × 0) + (- 0.154 × 0) + (1.154 × 0.4260) = 0.4916. El tercer valor de la Col. 6 es: (0.231 × 0) + (0.923 × 0) + (- 0.154 × 0.4916) + (1.154 × 0.9150) = 0.9802. Los valores restantes en la Col. 6 son calculados de una manera similar.
As in the previous example, the sums of Cols. 2, 4 and 7 confirm that the runoff volumes are appropriately conserved.
Como en el ejemplo anterior, las sumas de las Cols. 2, 4 y 7 confirman que los volúmenes de escorrentía se conservan adecuadamente.
Column 7 is the outflow hydrograph from the catchment.
La Columna 7 es el hidrograma del flujo de salida de la cuenca.
Assessment of Diffusion Wave Method / Evaluación del Método de la Onda de Difusión
The calculated outflow hydrograph peak is 0.9802 m3/s, and it occurs at 20 min. This value is very close to the maximum possible peak flow (1 m3/s), revealing that the amount of physical diffusion for this particular example is relatively small.
El pico del hidrograma del flujo de salida calculado es 0.9802 m3/s, y se produce a los 20 min. Este valor está muy cercano al flujo pico máximo posible (1 m3/s), revelando que la cantidad de la difusión física para este ejemplo en particular es relativamente pequeño.
To study the effect of grid size on the hydrograph calculated by the diffusion wave method,
a test similar to that of the
previous section is performed with the aid of a computer program.
Table 10-7 shows the results obtained by successive grid refinement, using program EH1000C.
It is shown that the results are essentially independent of grid size.
A coarse grid (one space increment in both planes and channel) results in a peak flow of 0.9802,
whereas a fine grid (16 increments in both planes and channel) results in a value of 0.9845.
However, it should be noted that the coarse-grid
solution (one space increment in planes and channel)
exhibits a small but perceptible amount of numerical dispersion, as
demonstrated by its peak (0.9802) being somewhat greater than the peak obtained with two increments (0.9716).
This is caused by the negative C0 in the planes (C0 =
Para estudiar el efecto del tamaño de la malla en el hidrograma calculado por el
método de la onda de difusión, una prueba similar a la de la sección anterior se lleva a cabo con la ayuda de un programa informático.
La Tabla 10-7 muestra los resultados obtenidos por el refinamiento de la malla sucesiva,
utilizando un programa EH1000C. Se muestra que los resultados son esencialmente independiente del tamaño de la malla. Una malla gruesa (un incremento de espacio en ambos planos y canal) da como resultado un flujo máximo de 0.9802, mientras que una malla fina (16 incrementos en ambos planos y canal) se traduce en un valor de 0.9845.
Sin embargo, debe tenerse en cuenta que la solución gruesa de la malla (incremento de un espacio en planos y canal) exhibe una pequeña pero perceptible cantidad de dispersión
numérica, como se demuestra por su pico (0.9802) es algo mayor que el pico obtenido con dos incrementos ( 0.9716). Esto es causado por el C0 negativo en los planos
(C0 =
| |||||||||||||||||||||||||||||||||||||
Unlike in the kinematic wave method, in the diffusion wave technique the numerical diffusion is matched to the physical problem. As in the case of stream channel routing (Section 10.4), this procedure works best when numerical dispersion is minimized, that is, when Courant numbers are kept reasonably close to 1. In practice, substantial deviations from this condition may lead to increased numerical dispersion and associated numerical instability. As with other finite difference schemes, a test of grid independence similar to that shown in Table 10-7 is necessary to verify the convergence of the numerical scheme.
Al contrario que en el método de onda cinemática, en la técnica de la onda de difusión la difusión numérica se corresponde con el problema físico. Al igual que en el caso de enrutamiento del canal de flujo (Sección 10.4), este procedimiento funciona mejor cuando se minimiza la dispersión numérica, es decir, cuando el número de Courant se mantienen razonablemente cerca de 1. En la práctica, las desviaciones importantes respecto de esta condición puede conducir a una mayor dispersión numérica y una inestabilidad numérica asociada. Al igual que con otros esquemas de diferencias finitas, una prueba de la independencia de la malla similar a la mostrada en la Tabla 10-7 es necesario verificar la convergencia del esquema numérico.
10.6 COMPARACIÓN DE MÉTODOS
|
|
Catchment routing techniques have evolved from the simple time-area methods to the more elaborate physically based kinematic and diffusion wave techniques. The variety of existing methods and techniques reflects the fact that no one method is applicable to all cases. Surface runoff in catchments is a complex phenomenon, and research continues to unveil improved ways of solving the problem.
Las técnicas de enrutamiento de captacioacute;n han evolucionado a partir de los métodos tiempo-área simples a las más elaboradas técnicas físicamente basadas en la cinemática y la onda de difusión. La variedad de los métodos y técnicas existentes refleja el hecho de que ningún método es aplicable a todos los casos. La escorrentía superficial en las cuencas es un fenómeno complejo, y la investigación continúa para dar a conocer mejores formas de resolver el problema.
In nature, catchments can be either small, midsize, or large. Runoff processes are nonlinear and distributed; nonlinear in the sense that the parameters do not increase in the same proportion as the flow, and distributed in the sense that the parameters vary within the catchment. Hydrographs originating in catchment runoff are generally concentrated, diffused, and dispersed. From the mathematical standpoint, concentration is a first-order process, diffusion a second-order process, and dispersion a third-order process [5]. Being a first-order process, runoff concentration is the primary mechanism; it is also referred to as translation or wave travel.
En la naturaleza, las cuencas pueden ser pequeñas, medianas o grandes. Los procesos de escorrentía no son lineales y distribuídas; no lineal en el sentido de que los parámetros no aumentan en la misma proporción que el flujo, y distribuidos en el sentido de que los parámetros varían dentro de la cuenca. Los hidrogramas originarios de la escorrentía de captación se concentran generalmente, difunden, y se dispersan. Desde el punto de vista matemático, la concentración es un proceso de primer orden, la difusión un proceso de segundo orden, y la dispersión un proceso de tercer orden [5]. Al ser un proceso de primer orden, la concentración de la escorrentía es el principal mecanismo; también se conoce como traslado o viaje de la onda.
For certain applications, diffusion also plays an important role-for instance, in the modeling of runoff response in catchments with mild slopes. Early description of the diffusion mechanism referred to it as storage. The usage is so widespread that it has been preserved in this book. In a routing context, diffusion and (longitudinal channel) storage have essentially the same meaning. Dispersion is a third order process; therefore, it is usually much smaller than runoff concentration and diffusion. Physical dispersion translates into wave steepening, a concept similar to that of skewness, or the third moment of a statistical distribution (Chapter 6).
Para ciertas aplicaciones, la difusión también juega un papel importante-por ejemplo, en el modelado de la respuesta de la escorrentía en cuencas con pendientes suaves. La descripción temprana del mecanismo de difusión se refirió a ella como almacenamiento. El uso es tan generalizado que se ha conservado en este libro. En un contexto de enrutamiento, la difusión y almacenamiento (canal longitudinal) tienen esencialmente el mismo significado. La dispersión es un tercer proceso de la orden; por lo tanto, por lo general es mucho menor que la concentración de la escorrentía y la difusión. La dispersión física se traduce en empinamiento de la onda, un concepto similar a la de asimetría, o el tercer momento de una distribución estadística (Capítulo 6).
The time-area method can calculate concentration but it cannot account for diffusion or dispersion. Therefore, the time-area method should be limited to small and midsize catchments where translation is by far the predominant mechanism. When used indiscriminately, the time-area method always overestimates the peak of the outflow hydrograph. If necessary, diffusion can be added by routing the time-area hydrograph through a linear reservoir. However, the storage constant would have to be determined either from measured data or by synthetic means. While the time-area method is a lumped method, it can be used as a component of larger network models which have a distributed structure [19].
El método de tiempo-área puede calcular la concentración, pero no puede dar cuenta de la difusión o dispersión. Por lo tanto, el método de tiempo-área se debe limitar a las pequeñas y medianas cuencas donde el traslado es por mucho el mecanismo predominante. Cuando se usa de manera indiscriminada, el método de tiempo-área siempre sobrestima el pico del hidrograma de flujo de salida. Si es necesario, la difusión puede ser añadido por el enrutamiento del hidrograma tiempo-área a través de un reservorio lineal. Sin embargo, la constante de almacenamiento tendría que estar determinado ya sea de datos medidos o por medios sentéticos. Mientras que el método de tiempo-área es un método globalizado, que puede ser utilizado como un componente de los modelos de redes más grandes que tienen una estructura distribuida [19].
In principle, the method of cascade of linear reservoirs accounts for runoff diffusion only. However, the connection of several linear reservoirs in series provides enough diffusion so that translation is actually being simulated by means of diffusion. The method is linear insofar as the routing parameters are determined by calibration. Nevertheless, by successive calibrations at different flow levels, from low to high, the method can be made to reflect the nonlinearity actually existing in nature. The method is lumped, but it can be used as a component of larger network models that have a distributed structure. The method has been successfully applied to very large basins (in excess of 10,000 km2), which exhibit substantial amounts of diffusion. For such large basins, the distributed models of the kinematic and diffusion type may be impractical due to the prohibitive amount of data required to properly specify the spatial diversity.
En principio, el método de cascada de los reservorios lineales representa sólo la difusión de escorrentía. Sin embargo, la conexión de varios reservorios lineales en serie proporciona suficiente difusión de modo que el traslado en realidad se simula por medio de difusión. El método es lineal en la medida que los parámetros de enrutamiento se determinan por calibración. Sin embargo, mediante calibraciones sucesivas en diferentes niveles de flujo, de baja a alta, el método puede hacerse para reflejar la no linealidad realmente existente en la naturaleza. El método se agrupa, pero puede ser usado como un componente de los modelos de redes más grandes que tienen una estructura distribuida. El método se ha aplicado con éxito a las cuencas muy grandes (de más de 10,000 km2), que presentan grandes cantidades de difusión. Para tales grandes cuencas, los modelos distribuidos del tipo cinemático y la difusión pueden ser poco prácticos debido a la cantidad prohibitiva de datos necesarios para especificar adecuadamente la diversidad espacial.
The kinematic wave model provides translation and diffusion, the latter, however, due only to the finite grid size. The method can be linear or nonlinear, and lumped or distributed, depending on the numerical scheme and input data. The method is applicable to small catchments with steep slopes where diffusion is small and can be controlled by grid refinement. Theoretically, the method could also be applicable to midsize catchments, as long as physical diffusion remains small. In practice, the larger the catchment, the more unlikely it is that physical diffusion is negligible.
El modelo de onda cinemática ofrece traslado y difusión, este último, sin embargo, debido únicamente al tamaño de la malla finita. El método puede ser lineal o no lineal, y agrupado o distribuida, dependiendo de los esquemas numéricos y de entrada. El método es aplicable a pequeñas cuencas con pendientes pronunciadas donde la difusión es pequeño y puede ser controlado por el refinamiento de la malla. En teoría, el método también podría ser aplicable en cuancas de tamaño medio, siempre que la difusión física sigue siendo pequeño. En la práctica, cuanto mayor sea la cuenca, lo más probable es que la difusión física es insignificante.
The distributed nature of kinematic wave models results in substantial data needs; the use of average parameters would render the model lumped, with the consequent loss of detail. Another important consideration in kinematic wave models is the validity of the geometric configuration. For instance, two-plane descriptions are adequate as long as the catchment geometry fits the two-plane model configuration. Otherwise, a certain amount of lumping would be introduced by the model's inability to properly account for the physical detail. In practice, the larger the catchment, the more difficult it is to fit catchments within two-plane descriptions. Multiple-plane descriptions are possible but invariably lead to additional complexity [8].
La naturaleza distribuida de modelos de onda cinemáticas resulta en las necesidades de datos sustanciales; el uso de parámetros medios har´a que el modelo agrupado, con la consecuente pérdida de detalles. Otra consideración importante en los modelos de onda cinemática es la validez de la configuración geométrica. Por ejemplo, las descripciones de dos planos son adecuados siempre y cuando la geometrí a de cuenca se ajusta a la configuración del modelo de dos planos. De lo contrario, una cierta cantidad de formación de grumos se introduciría por la incapacidad del modelo para tener en cuenta adecuadamente para el detalle físico. En la pr´ctica, cuanto mayor sea la cuenca, lo más difícil es adaptarse a las cuencas en las descripciones de dos planos. Descripciones de múltiples planos son posibles pero invariablemente conducir a la complejidad adicional [8].
The diffusion wave technique (Muskingum-Cunge scheme) provides translation and diffusion and, unlike the kinematic wave model, its solution is generally independent of grid size. Therefore, it is applicable to catchments with substantial amounts of physical diffusion, either small catchments of mild slope or midsize catchments with average slopes. The method is linear or nonlinear, and lumped or distributed, depending on the numerical scheme and input data. As with kinematic models, the validity of the geometric configuration is important in diffusion wave catchment models. Unless the model's geometric abstraction is a reasonable representation of the catchment's actual geometry, the degree of lumping introduced may tend to mask the distributed nature of the model.
La técnica de onda de difusión (esquema de Muskingum-Cunge) ofrece traslado y difusión y, a diferencia del modelo de onda cinemática, su solución es generalmente independiente del tamaño de la rejilla. Por lo tanto, es aplicable a las cuencas con cantidades sustanciales de difusión física, tanto las pequeñas cuencas pendiente mediana o cuencas de tamaño medianas con pendientes medias. El método es lineal o no lineal, y agrupado o distribuido, dependiendo de los esquemas numéricos y datos de entrada. Al igual que con modelos cinemáticos, la validez de la configuración geométrica es importante en modelos de captación de onda de difusión. A menos que la abstracción geométrica del modelo es una representación razonable de la geometría real de la cuenca, el grado de formación de grumos introducido puede tender a enmascarar la naturaleza distribuida del modelo.
The preceding comments have referred specifically to catchment routing, i.e., the conversion of effective rainfall into runoff. In practice, comparative evaluations of the performance of catchment routing methods/models are hampered by the fact that it is seldom possible to determine effective rainfall with any degree of certainty. Hydrologic abstractions are time-variant, distributed, and nonlinear. Therefore, a proper estimation of hydrologic abstractions is crucial to the performance evaluation of catchment routing models.
Los comentarios anteriores se han referido específicamente para el tránsito de cuencas, es decir, la conversión de precipitación efectiva en escorrentía. En la pr´ctica, las evaluaciones comparativas del funcionamiento de los métodos/modelos del tránsito de cuencas están obstaculizados por el hecho de que rara vez es posible determinar la precipitación efectiva con algún grado de certeza. Las abstracciones hidrológicas son de tiempo-variante, distribuido, y no lineal. Por lo tanto, una estimación adecuada de abstracciones hidrológicas es crucial para la evaluación del desempeño de los modelos de tránsito de cuencas.
From this discussion, it can be concluded that no one method or model is suitable for all applications. All have strengths and weaknesses; they are either simple or complex, and suffer from lack of detail or require a substantial amount of data for their successful operation. In practice, the choice of catchment routing method remains one of individual preference and experience.
A partir de esta discusión, se puede concluir que ningún método o modelo es adecuado para todas las aplicaciones. Todos tienen puntos fuertes y débiles; son simples o complejos, y sufren de falta de detalle o requieren una cantidad considerable de datos para su buen funcionamiento. En la práctica, la elección del método de tránsit de cuencas sigue siendo uno de preferencia y experiencia individual.
PREGUNTAS
|
|
-
What is the difference between hydrologic and hydraulic methods of catchment routing?
¿Cuál es la diferencia entre los métodos hidrológicos e hidráulicos del tránsito de cuencas?
What are catchment isochrones? How are they determined?
¿Cuáles son las cuencas isócronas? ¿Cómo se determinan?
How is time of concentration defined when using hydrographs generated by the time-area method?
¿Cómo es tiempo de concentración definido al utilizar hidrogramas generados por el método de tiempo-área?
When can the Clark unit hydrograph be considered synthetic? Explain.
¿Cuándo se puede considerar el hidrograma unitario de Clark sintético? Explicar.
What is the difference between translation and diffusion? How are the time-area and rational methods related?
¿Cuál es la diferencia entre el traslado y la difusión? ¿Cómo están relacionados los métodos tiempo-área y racional?
How can the linear reservoir storage coefficient be determined for runoff data?
¿Cómo se puede determinar el coeficiente de almacenamiento del reservorio lineal para los datos de escorrentía?
What is the principle behind the method of cascade of linear reservoirs used in catchment routing?
¿Cuál es el principio detrás del método de cascada de los reservorios lineales usados en el tránsito de cuencas?
Why is it necessary to use two schemes in catchment routing using first-order kinematic wave techniques?
¿Por qué es necesario el uso de dos esquemas en tránsito de cuencas mediante técnicas de onda cinemática de primer orden?
Why is a kinematic wave solution using numerical techniques usually grid-dependent? Why is the diffusion wave solution grid-independent?
¿Por qué es una solución de onda cinemática utilizando técnicas numéricas generalmente de rejilla dependiente? ¿Por qué es la solución de onda de difusión de rejilla independiente?
PROBLEMAS
|
|
A 45-km2 catchment has a 6-h time of concentration with isochrones at 2-h intervals, resulting in the following time-area histogram:
Una cuenca de 45 km2 tiene un tiempo de 6-h de concentración con isócronas a intervalos de 2-h, lo que resulta en el siguiente histograma de tiempo-área:
Time / Tiempo (h) 0-2 2-4 4-6 Area / Área (km2) 9 21 15 Use the time-area method to calculate the outflow hydrograph from the following effective storm pattern:
Utilizar el método de tiempo-área para calcular el hidrograma de flujo de salida desde el siguiente patrón de tormenta efectiva:
Time / Tiempo (h) 0-2 2-4 4-6 6-8 8-10 10-12 Effective rainfall / Precipitación efectiva (cm/h) 0.5 1.0 2.0 3.0 1.0 0.5 Use a spreadsheet. Verify your results with ONLINE ROUTING06.
Usar una hoja de cálculo. Verificar sus resultados con ONLINE ROUTING06.
A 68-km2 catchment has a 4-h time of concentration with isochrones at 1-h intervals resulting in the following time-area histogram:
Una cuenca de 68 km2 tiene un tiempo de 4-h de concentración con isócronas a intervalos de 1-h resultantes en el siguiente histograma de tiempo-área:
Time / Tiempo (h) 0-1 1-2 2-3 3-4 Area /Área (km2) 12 19 26 11 Use the time-area method to calculate the outflow hydrograph from the following storm:
Utilizar el método de tiempo-área para calcular el hidrograma de flujo salida de la siguiente tormenta:
Time / Tiempo (h) 0-1 1-2 2-3 3-4 4-5 5-6 Total rainfall / Precipitación total (cm/h) 1 2 4 3 2 1 The runoff curve number is CN = 75. Use a spreadsheet. Verify your results with ONLINE ROUTING06.
El número de curva de escorrentía es CN = 75. Utilizar una hoja de cálculo. Verificar sus resultados con ONLINE ROUTING06.
An 82-km2 catchment has the following characteristics:
Una cuenca de 82 km2 tiene las siguientes características:
Time / Tiempo (h) 0-1 1-2 2-3 3-4 4-5 5-6 Area / Área (km2) 14 22 29 17 0 0 Effective rainfall / Precipitación efectiva (cm/h) 0.8 1.2 1.3 2.1 0.7 0.5 Using a spreadsheet, calculate the outflow hydrograph by the time-area method. Verify your results with ONLINE ROUTING06.
Usar una hoja de cálculo, calcular el hidrograma de flujo de salida por el método de tiempo-área. Verificar sus resultados con ONLINE ROUTING06.
Use the Clark method with a spreadsheet to derive a 3-h unit hydrograph for a catchment with the following time-area diagram:
Usar el método de Clark con una hoja de cálculo para derivar un hidrograma unitario de 3-h de una cuenca con el siguiente diagrama de tiempo-área:
Time / Tiempo (h) 0-3 3-6 6-9 9-12 Area / Área (km2) 57 72 39 15 Use Δt = 3 h and K = 3 h. Verify your results with ONLINE ROUTING07.
Usar Δt = 3 h and K = 3 h. Verificar sus resultados con ONLINE ROUTING07.
Use the Clark method with a spreadsheet to derive a 1-h unit hydrograph for a catchment with the following time-area diagram:
Usar el método de Clark con una hoja de cálculo para derivar un hidrograma unitario de 1-h para una cuenca con el siguiente diagrama de tiempo-área:
Time / Tiempo (h) 0-1 1-2 2-3 3-4 4-5 5-6 Area / Área (km2) 12 20 42 66 30 16 Use Δt = 1 h and K = 2 h. Verify your results with ONLINE ROUTING07.
Usar Δt = 1 h and K = 2 h. Verificar sus resultados con ONLINE ROUTING07.
Use the Clark method with a spreadsheet to derive a 2-h unit hydrograph for a catchment with the following time-area diagram:
Usar el método de Clark con una hoja de cálculo para derivar un hidrograma unitario de 2-h para una cuenca con el siguiente diagrama de tiempo-área:
Time / Tiempo (h) 0-1 1-2 2-3 3-4 4-5 5-6 Area / Área (km2) 10 20 30 20 12 8 Use Δt = 1 h and K = 4 h. Verify your results with ONLINE ROUTING07.
Usar Δt = 1 h and K = 4 h. Verificar sus resultados con ONLINE ROUTING07.
The 2-h unit hydrograph for a 92-km2 catchment is the following:
El hidrograma unitario de 2-h para una cuenca de 92 km2 es el siguiente:
Time / Tiempo (h) 0 2 4 6 8 10 12 14 Flow / Flujo (m3/s) 0 2.778 8.611 14.333 19.433 21.938 20.942 15.897 Time / Tiempo (h) 16 18 20 22 24 26 28 30 Flow / Flujo (m3/s) 9.538 5.722 3.433 2.061 1.236 0.742 0.444 0.267 Given the following time-area diagram, what is the linear reservoir storage constant in the Clark method?
Dado el siguiente diagrama de tiempo-área, cuál es la constante de almacenamiento del reservorio lineal en el método de Clark?
Time / Tiempo (h) 0-2 2-4 4-6 6-8 8-10 10-12 Area / Área (km2) 10 15 18 21 16 12 A 1-h unit hydrograph derived from measured data has the following ordinates:
Un hidrograma unitario de 1-h derivado de los datos de medición tiene las siguientes coordenadas:
Time / Tiempo (h) 0 1 2 3 4 5 6 7 Flow / Flujo (m3/s) 0 7 22 48 60 90 74 47 Time / Tiempo (h) 8 9 10 11 12 13 14 Flow / Flujo (m3/s) 28 17 10 6 4 3 2 Assuming a time of concentration tc = 6 h, calculate the linear reservoir storage constant in the Clark method.
Suponiendo un tiempo de concentración tc = 6 h, calcular la constante de almacenamiento del reservorio lineal en el método de Clark.
Using ONLINE ROUTING08, route the effective rainfall hyetograph of Example 10-3 (with time interval Δt = 6 h) using:
(a) K = 12 h and N = 4; and (b) K = 18 h and N = 3.Usando ONLINE ROUTING08, la ruta del hyetograma de precipitación efectiva del Ejemplo 10.3 (con intervalo de tiempo Δt = 6 h) using:
(a) K = 12 h y N = 4; y (b) K = 18 h y N = 3.Use ONLINE ROUTING08 to route the following storm hyetograph through a 535-km2 catchment.
Usar ONLINE ROUTING08 para la ruta del siguiente hyetograma de tormenta a través de una cuenca de 535-km2.
Time / Tiempo (h) 0-6 6-12 12-18 18-24 Effective rainfall depth / Profundidad de precipitación efectiva (cm) 1.0 1.5 2.5 1.2 Effective rainfall depth / Profundidad de precipitación efectiva (cm/hr) 0.1667 0.2500 0.4167 0.2000 Set K = 12 h and N = 3. Report peak outflow and time-to-peak.
Establecer K = 12 h and N = 3. Reportar el flujo de salida pico y tiempo-pico.
Using the method of cascade of linear reservoirs, derive a 3-h unit hydrograph for a 432-km2 basin. Assume Δt = 3 h, K = 9 h and two reservoirs (N = 2). Verify the results with ONLINE ROUTING08.
Utilizando el método de cascada de reservorios lineales, derivar un hidrograma unitario de 3-h para una cuenca de 432-km2. Suponer Δt = 3 h, K = 9 h y dos reservorios (N = 2). Verificar los resultados con ONLINE ROUTING08.
Using the method of cascade of linear reservoirs, derive a 6-h unit hydrograph for a 1235-km2 basin. Assume Δt = 6 h, K = 6 h and N = 4. Verify the results with ONLINE ROUTING08.
Utilizando el método de cascada de reservorios lineales, derivar un hidrograma unitario de 6-h para una cuenca de 1235-km2 Asumir Δt = 6 h, K = 6 h y N = 4. Verificar los resultados con ONLINE ROUTING08.
Derivar la Ec. 10-16.
Derivar la Ec. 10-17.
Derivar la Ec. 10-20.
BIBLIOGRAFÍA
|
|
Agricultural Research Service, U.S. Department of Agriculture. (1973). "Linear Theory of Hydrologic Systems," Technical Bulletin No. 1468, J. C. I. Dooge, autor), Washington, D.C.
Clark, C. O. (1945). "Storage and the Unit Hydrograph," Transactions. ASCE, Vol. 110. pp. 1416-1446.
Cordery, 1. (1968). "Synthetic Unit Graphs for Small Catchments in Eastern New South Wales," Civil Engineering Transactions of the Institution of Engineers, Australia, Vol. 10, pp. 47-58.
Eaton, T. D. (1954) . "The Derivation and Synthesis of Unit Hydrographs When Rainfall Records Are Inadequate," Institution of Engineers, Australia, Vol. 26, pp. 239-246.
Ferrick, M. G., J. Bilmes, y S. E. Long. (1983). "Analysis of a Diffusion Wave Flow Routing Model with Application to Flow in Tailwaters," U.S. Army Corps of Engineers, Cold Regions Research and Engineering Laboratory, CRREL Report 83-7, Marzo.
Hromadka, T. V. , R. H. McCuen, y C. C. Yen. (1987). "Comparison of Overland Flow Hydrograph Models," Journal of Hydraulic Engineering, ASCE. Vol. 113, No. 11, Noviembre. pp. 1422-1440.
Hydrologic Engineering Center, U.S. Army Corps of Engineers. (1990). "HEC-l, Flood Hydrograph Package, User's Manual," Version 4.0, Septiembre.
Kibler, D. F., y D. A. Woolhiser. (1970). "The Kinematic Cascade as a Hydrologic Model," Colorado State University Hydrology Paper No. 39, Fort Collins, Colorado.
Lighthill, M. J., y G. B. Whitham. (1955). "On Kinematic Waves. 1. Flood Movement in Long Rivers," Proceedings. Royal Society, London, Vol. A229. Mayo, pp. 281-316.
Nash, J. E. (1958). "The Form of the Instantaneous Unit Hydrograph," International Association for Scientific Hydrology, Publication No. 42, No.3, pp. 114-118.
O'Kelly, 1. J. (1955). "The Employment of Unit Hydrograph to Determine the Flows of Irish Arterial Drainage Channels," Proceedings of the Institution of Civil Engineers, Dublin, Irlanda, Vol. 4, No.3, pp. 365-412.
Ponce, V. M., R. M. Li, y D. B. Simons. (1978). "Applicability of Kinematic and Diffusion Models," Journal of the Hydraulics Division, ASCE, Vol. 104, No. HY3, Marzo, pp. 353-360.
Ponce, V. M., y D. Windingland. (1985). "Kinematic Shock: Sensitivity Analysis," Journal of Hydraulic Engineering, ASCE. Vol. 111, No. 4, April, pp. 600-611.
Ponce, V. M. (1986). "Diffusion Wave Modeling of Catchment Dynamics," Journal of Hydraulic Engineering, ASCE, Vol. 112, No. 8, August, pp. 716-727.
Ponce, V. M., and P. T. Huston. 1994. "New perspective on the convection-diffusion-dispersion equation," Water Resources Research, Vol. 30, No. 5, Mayo, pp. 1619-1620.
Orlandini, S., y R. Rosso. (1996). "Diffusion Wave Modeling of Distributed Catchment Dynamics," Journal of Hydrologic Engineering, ASCE, Vol. 1, No. 3, Julio, pp. 103-113.
Rao, R. A., J. W. Delleur, y B. S. Sarma. (1972). "Conceptual Hydrologic Models for Urbanizing Basins," Journal of the Hydraulics Division, ASCE, Vol. 98, No. HY7, Julio, pp. 1205-1220.
Singh, V. P. (1988). Hydrologic Systems. Rainfall-Runoff Modeling, Vol. 1. Englewood Cliffs, N.J.: Prentice-Hall.
Stall, J. B., y Terstriep, M. L. (1972). "Storm-Sewer Design: An Evaluation of the RRL Method," EPA Technology Series EPA-R2-72-068, October.
U.S. Army Engineer Division, North Pacific Division. (1986). "Program Description and User Manual for SSARR Model, Streamflow Synthesis and Reservoir Regulation," Portland, Oregon, Abril.
Wooding, R. A. (1965). "A Hydraulic Model for the Catchment-stream Problem, 1. Kinematic Wave Theory," Journal of Hydrology, Vol. 3, pp. 254-267.
Wooding, R. A. (1965). "A Hydraulic Model for the Catchment-stream Problem, II. Numerical Solutions," Journal of Hydrology, Vol. 3, 1965, pp. 268-282.
Wooding, R. A. (1966). "A Hydraulic Model for the Catchment-stream Problem, III. Comparison with Runoff Observations," Journal of Hydrology, Vol. 4, pp. 21-37.
Woolhiser, D. A., y Liggett, J. A. (1967). "Unsteady One-dimensional Flow Over a Plane: The Rising Hydrograph," Water Resources Research, Vol. 3, No.3, pp. 753-771.
SUGGESTED READINGS
Agricultural Research Service, U.S. Department of Agriculture. (1973). "Linear Theory of Hydrologic Systems," Technical Bulletin No. 1468, (J. C. I. Dooge, autor), Washington, D.C.
Clark, C. O. (1945). "Storage and the Unit Hydrograph," Transactions, ASCE, Vol. 110, 1945, pp. 1416-1446.
Hydrologic Engineering Center, U.S. Army Corps of Engineers. (1990). "HEC-1, Flood Hydrograph Package, User's Manual," Version 4.0, Septiembre.
U.S. Army Engineer Division, North Pacific Division. (1986). "Program Description and User Manual for SSARR Model, Streamflow Synthesis and Reservoir Regulation," Portland, Oregon, Abril.
Wooding, R. A. (1965). "A Hydraulic Model for the Catchment-stream Problem, I. Kinematic Wave Theory," Journal of Hydrology, Vol. 3, 1965, pp. 254-267.
| http://engineeringhydrology.sdsu.edu |
|
160517 16:00 |