|
|
|
CAPÍTULO 11: ESCOAMENTO INSTÁVEL RAPIDAMENTE VARIADO |
11.1 ONDAS SUPERFICIAIS
|
|
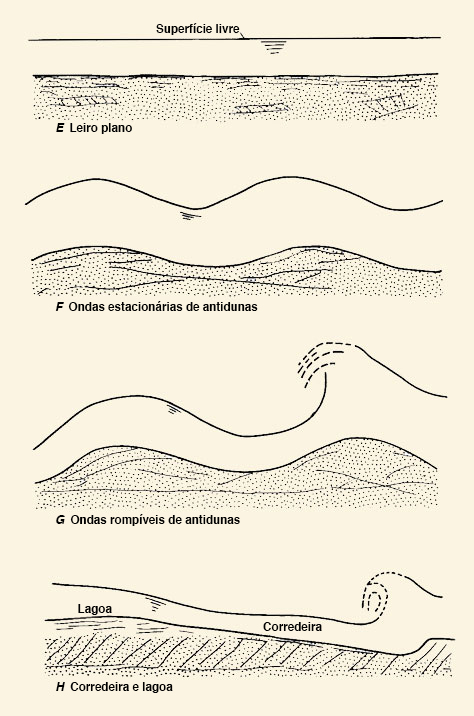
As ondas superficiais são recursos de fluxo de canal aberto instáveis que ocorrem normalmente nos fluxos com alto número de Froude. A Figura 11-1 mostra uma onda de superfície no rio Hassayampa, perto de Morristown, Arizona (Phillips e Ingersoll, 1998). A perturbação é uma onda que se propaga lentamente à jusante e que indica as características hidráulicas em canais aluviais em condições de fluxo de regime super crítico (Fig. 11-2) (Simons e Richardson, 1966).
|
|
A Figura 11-3 mostra o rio Santa Catarina, em Monterrey, Nuevo Leon, México, durante a passagem do furacão Gilbert, em 17 de setembro de 1988. As grandes ondas superficiais observadas são uma indicação dos altos fluxos de número de Froude que provavelmente prevaleceram durante a passagem do dilúvio.
|
11.2 ONDULAÇÕES ACENTUADAS
|
|
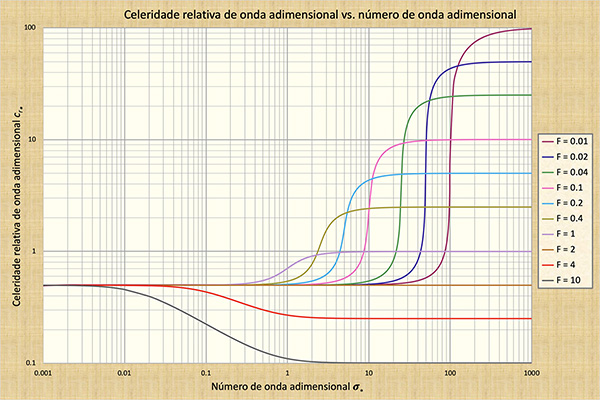
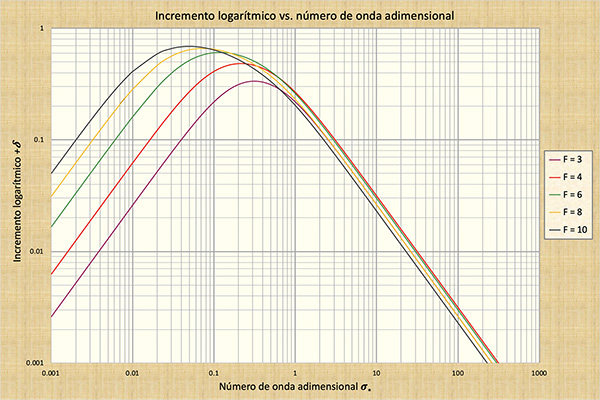
As ondulações acentuadas são perturbações criadas por fechamentos repentinos de comportas ou mudanças rápidas no estágio (nível d'água) ou profundidade do fluxo. Normalmente, uma onda não atenua prontamente, viajando ao longo do canal por uma distância considerável. As ondulações acentuadas são evitadas abrindo as comportas lentamente, para minimizar a possibilidade de mudanças bruscas de estágio ou profundidade. A atenuação da onda aumenta à medida que o número de onda adimensional diminui do correspondente para uma onda dinâmica verdadeira (com celeridade constante, ou seja, para o lado direito do espectro do número de onda), para o correspondente a uma onda dinâmica mista (com celeridade variável, ou seja, ao longo da parte superior lado descendente da curva S) (Fig. 11-4).
|
Com base no critério acima, uma primeira aproximação para o momento da abertura To de uma porta do canal, para evitar picos de tensão, é (Ponce et al., 1999):
|
k uo To ≥ _______ g So | (11-1) |
Em que: uo = velocidade de fluxo;
So = declividade do canal;
g = aceleração da gravidade;
k = constante, que vaira em função do número de Froude (Tabela 11-1).
| ||||||||||||||
11.3 CHOQUES CINEMÁTICOS
|
|
Os choques cinemáticos são ondas cinemáticas que se abrem ao ponto de se tornarem, para todos os efeitos práticos, uma parede de água, com uma face quase vertical. Na verdade, o choque não é uma descontinuidade perfeita. No entanto, sua espessura é relativamente pequena em comparação ao comprimento de onda da perturbação (Lighthill e Whitham, 1955).
As ondas cinemáticas viajam à jusante e podem se inclinar ou achatar, dependendo de sua interação com a geometria da seção transversal. Somente ondas cinemáticas que se inclinam podem se transformar em choques cinemáticos. Enquanto as ondas cinemáticas variam gradualmente, os choques cinemáticos variam rapidamente.
O desenvolvimento de um choque cinemático está em função das seguintes condições de fluxo (Ponce e Windingland, 1985):
Tipo de onda
Quanto mais cinemática for uma onda (ou seja, quanto menor o número de onda adimensional), menor será sua tendência a atenuar e, portanto, maior será a sua tendência a se inclinar.
Quantidade de fluxo básico
Quanto menor a taxa de fluxo da base ao pico, maior será a tendência da onda se tornar mais inclinada. Isso ocorre devido às não linearidades das ondas (fluxos maiores da calha fluvial viajam com maiores celeridades).
Regime de fluxo
Fluxos com alto número de Froude têm menos tendência a atenuar distúrbios. Portanto, quanto maior o número de Froude, menor a atenuação. No limite, à medida que o fluxo se aproxima do número Vedernikov V = 1 (isto é, F = 2 para atrito Chezy em canais hidraulicamente amplos), o fluxo se torna neutralmente estável e a atenuação é reduzida a zero.
Tipo de seção transversal
Canais hidraulicamente largos, para os quais o expoente de classificação β = 1,5 (atrito de Chezy), têm uma tendência maior de aguçar os canais triangulares, para os quais β = 1,25. Canais inerentemente estáveis, para os quais β = 1, não têm tendência a se inclinar (consulte a Tabela 10-3 para outros valores aplicáveis de β).
Assim, choques cinemáticos se desenvolverão em situações de campo envolvendo: (a) uma onda cinemática, (b) um canal efêmero (fluxo básico zero), (c) uma alta vazão (uma inundação) e (d) um canal hidraulicamente amplo. Pode ser o caso de uma grande explosão de nuvem que concentra rapidamente o fluxo através de um canyon em uma região semiárida.
Uma inundação repentina e bem documentada, que provavelmente foi um choque cinemático, ocorreu em 26 de julho de 1981 no riacho Tanque Verde, um afluente do rio Santa Cruz, no leste do Arizona, EUA. A inundação, que matou oito pessoas, foi, segundo todos os relatos, apenas uma inundação com período de retorno de dois anos. No entanto, a súbita inundação que, segundo relatos dos sobreviventes, atingiu uma "parede d'água", resultou em um número substancial de perda de vidas (Hjalmarson, 1984).
Choques cinemáticos foram observados com certa frequência em cálculos de transbordamento laboratoriais. Sabe-se que esses cálculos são propícios ao desenvolvimento de choque cinemático (Kibler e Woolhiser, 1970). A presença de choque é atribuída à regularidade espacial prescrita, que é necessária para possibilitar o tratamento do problema.
11.4 ONDAS DE ROLO
|
|
As ondas de rolo se desenvolvem nos escoamentos abertos quando o número Vedernikov V > 1 (Craya, 1952; Chow, 1959). Nos canais naturais, a condição V > 1 raramente é cumprida (Jarrett, 1982). Assim, as ondas de rolo são restritas a canais artificiais revestidos com concreto ou alvenaria. Normalmente, as ondas de rolo aparecem como um trem de ondas que se move à jusante, como mostrado na Fig. 1-7 (Capítulo 1).
O Vedernikov é definido como a razão entre a celeridade relativa das ondas cinemáticas e a celeridade dinâmica relativa das ondas (Ponce, 1991):
(β - 1) u | (11-2) |
Em que: β = expoente da curva-chave (Eq. 10-52);
u = velocidade média;
h = profundidade do fluxo;
g = aceleração da gravidade.
A ondas de rolo ocorrem quando a celeridade relativa da onda cinemática excede a celeridade relativa da onda dinâmica. Como as ondas cinemáticas transportam massa e as ondas dinâmicas (verdadeiras) transportam energia, as ondas rolantes ocorrem no limiar em que a massa e a energia são transportadas na mesma velocidade. Na prática, ondas de rolagem ocorrem em canais artificiais íngremes quando o número Vedernikov V > 1 (Fig. 11-5).
|
A condição
|
Um exemplo curioso e um tanto extremo de ondas de rolagem em um canal urbano íngreme é visto neste vídeo de um evento no rio Huayñajahuira, La Paz, Bolívia, em 25 de fevereiro de 2016, às 17:30.
| Assista o video (em inglês) |
11.5 ONDAS DE MARÉ
|
|
As pororocas são características de fluxo de superfície livre instáveis, rapidamente variadas, que ocorrem em certos rios nas proximidades de seus estuários. As ondas de maré ocorrem em um estuário para uma grande faixa de marés ou próximos a qualquer um dos equinócios (20 de março e 22 de setembro). Se a onda de maré é capaz de se mover à montante do rio propriamente dita e se transformar em um poço reconhecível de profundidade finita, depende em grande parte da geometria da seção transversal do estuário. As pororocas têm mais probabilidade de se formar em canais suaves e hidraulicamente amplos, de profundidade relativamente constante.
|
Grandes pororocas foram observadas no rio Araguari, no Brasil (Fig. 11-7), no rio Chien Tang, na China (Fig. 11-8) e em outros estuários selecionados ao redor do mundo. Chow (1959) descreveu o furo de Hangchow em Haining, no rio Chien Tang, na China. A frente de onda tinha cerca de 16 pés de altura, viajando em alta velocidade. Sete milhas depois de distinguir-se pela primeira vez no horizonte, a onda havia passado. A água atingiu uma altura final de cerca de 28 pés em 30 minutos. A largura do rio no ponto de observação era de cerca de 1 milha.
|
11.6 ESCOAMENTO DE DETRITOS
|
|
Os escoamentos de detritos são acúmulos repentinos de escoamento contendo grandes quantidades de partículas de sedimentos, geralmente no tamanho de pedregulhos ou ainda maior. O Escoamento de Detritos viaja rio abaixo a grandes velocidades, destruindo tudo em seu caminho e ameaçando vidas e propriedades (Fig. 11-9).
|
O escoamento de detritos é induzido por chuvas intensas, mas também pode ser desencadeado por terremotos. No sul da Califórnia, ao longo da base das montanhas de San Gabriel, a leste de Los Angeles, os fluxos de detritos induzidos pela chuva ocorrem com regularidade previsível. Os fatores que levam à formação desses fluxos de detritos são:
Tectonismo
As montanhas de San Gabriel estão entre as faixas mais tectonicamente ativas dos Estados Unidos (Fig. 11-10). A elevação leva ao declive, que aumenta as forças gravitacionais e maximiza o potencial de erosão.

Wikimedia Commons Fig. 11-10 Montanhas de San Gabriel, na parte sul da Califórnia.
Ecossistema chaparral
O ecossistema chaparral é endêmico da região, sobrevivendo a longas secas, desenvolvendo adaptações singulares que dependem do revestimento protetor de cera para suprimir a evapotranspiração (Fig. 11-11) (McPhee, 1989).

Fig. 11-11 Ecossistema Chaparral da Tierra del Sol, condado de San Diego, Califórnia.
Vento
A região abriga os ventos de Santa Ana, que proporcionam um clima de incêndio instantâneo, apresentando ventos secos que podem facilmente chegar a mais de 65 quilômetros por hora.
Fogo
O fogo segue o vento após uma longa seca, com o chaparral não queimando há mais de 30 anos (Fig. 11-12).

Fig. 11-12 Sequência do fogo de Shockey, na Tierra del Sol, Califórnia, em 27 de Setembro de 2012.
Chuva
A chuva segue o fogo devido às partículas de cinzas no ar, promovendo coalescência e formação de gotas de chuva.
As encostas íngremes cobertas por vegetação chaparral, seguidas por uma sequência de vento, fogo e chuva, desencadeiam o fluxo de detritos na região sul da Califórnia. Durante o incêndio, as substâncias semelhantes à cera evaporam na superfície e recondensam-se a uma profundidade de 10 a 50 mm da superfície, abaixo da qual o solo não é molhável, ou seja, é hidrofóbico. O acúmulo de chuvas intensas, superiores a 25 mm por hora, imediatamente abaixo da superfície e acima da camada não molhável, leva ao arrastamento de grandes quantidades de sedimentos que constituem os fluxos de detritos. Um fluxo típico de detritos induzidos pela chuva no sul da Califórnia pode levar de 10 a 50 mm de solo em poucas horas. A título de comparação, as taxas normais de erosão são tipicamente inferiores a 1 mm por ano.
Escorregamentos provocadas por terremotos
Fluxos maciços de detritos também podem ser desencadeados por terremotos. Esse foi o caso do escorregamento de Huascaran em 30 de maio de 1970, no Peru, que enterrou a cidade de Yungay, matando mais de 20.000 pessoas (Fig. 11-13). Desde então, a cidade foi reconstruída em um local ao norte da antiga municipalidade.
|
11.7 LAHARES
|
|
Os lahares são fluxos de detritos desencadeados pelo derretimento da neve, após uma erupção vulcânica e subsequente derretimento repentino da calota da neve. A palavra lahar se originou na Indonésia, onde o fenômeno é comum. Os lahares têm consistência, viscosidade e aproximadamente a mesma densidade que o concreto, sendo fluido quando em movimento e sólido quando parado (Fig. 11-14).
|
O lahar pode ser maciço e mortal, como mostra a erupção do vulcão Nevado del Ruiz, em 13 de novembro de 1985, na Colômbia. Quatro lahares desceram os vales dos rios nos flancos do vulcão. O maior deles praticamente destruiu a cidade de Armero, enterrando-a sob 5 m de lama e detritos, matando mais de 75% de seus 28.700 habitantes (Fig. 11-15).
|
QUESTÕES
|
|
Quais formas de leito se desenvolvem sob regime superior no fluxo de canais aluviais?
Quando os picos se formam no fluxo de canal aberto?
O que é um choque cinemático?
Que condições são necessárias para que uma onda cinemática se transforme em um choque cinemático?
Quando as ondas de rolo se desenvolvem?
As ondas de rolo se desenvolvem sempre em canais íngremes?
Onde as pororocas têm maior probabilidade de se formar?
O que é um fluxo de detritos?
Quais condições são favoráveis para o desenvolvimento de fluxos de detritos no clima do sul da Califórnia?
O que é um lahar?
PROBLEMAS
|
|
Calcule o tempo de abertura de uma comporta de um canal nas seguintes condições de escoamento: profundidade do fluxo
do = 1,2 m, velocidade do fluxo uo = 1,5 m e inclinação do canal So = 0,001.Um determinado canal possui um fator de atrito sem dimensão de Darcy-Weisbach f = 0,0035. A inclinação do canal é So = 0,014. Determine se essa condição de fluxo é estável para o atrito de Chezy em um canal hidraulicamente amplo.
REFERÊNCIAS
|
|
Brock, R. R. 1967. Development of roll waves in open channels. Report No. KH-R-16, W. M. Keck Laboratory of Hydraulics e Water Resources, California Institute of Technology, Pasadena, California,
Chow, V. T. 1959. Open-channel Hydraulics. McGraw Hill, New York.
Cornish, V. 1907. Progressive waves in rivers. The Geographical Journal. Vol. 29, No. 1, January, 23-31.
Craya, A. 1952. The criterion for the possibility of roll-wave formation. Gravity Waves, Circular No. 521, National Bureau of Standards, Washington, D.C. 141-151.
Hjalmarson, H. W. 1984. Flash flood in Tanque Verde Creek, Tucson, Arizona. Journal of Hydraulic Engineering, Vol. 110, No. 12, 1841-1852.
Jarrett, R. D. 1984. Hydraulics of high-gradient streams. Journal of Hydraulic Engineering, Vol. 110, No. 11, 1519-1539.
Kibler, D. F., e D. A. Woolhiser. 1970. The kinematic cascade as a hydrologic model. Hydrology Paper No. 39, Colorado State University, Ft. Collins, Colorado.
Lighthill, M. J., e G. B. Whitham. 1955. On kinematic waves: I. Flood movement in long rivers. Proceedings, Royal Society of London, Series A, 229, 281-316.
McPhee, J. 1989. The Control of Nature. Farrar Straus Giroux, New York.
Ponce, V, M., e D. Windingland. 1985. Kinematic shock: Sensitivity analysis. Journal of Hydraulic Engineering, ASCE, Vol. 111, No. 4, April, 600-611.
Ponce, V. M. 1991. New perspective on the Vedernikov number. Water Resources Research, Vol. 27, No. 7, 1777-1779, July.
Ponce, V, M., e M. P. Maisner. 1993. Verification of theory of roll wave formation. Journal of Hydraulic Engineering, ASCE, Vol. 119, No. 6, June, 768-773.
Ponce, V, M., Y. R. S.Rao, e N. M. Mansury. 1999. Time of opening of irrigation canal gates. Journal of Hydraulic Engineering, ASCE, Vol. 125, No. 9, September, 979-980.
Phillips, J. V., e T. L. Ingersoll. 1998. Verification of roughness coefficients for selected natural e constructed stream channels in Arizona. U.S. Geological Survey Professional Paper 1584, Washington, D.C.
Simons, D. B., e E. V. Richardson. 1966. Resistance to flow in alluvial channels. U.S. Geological Survey Professional Paper 422-J, Washington, D.C.
| http://hidraulicadecanaisabertos.sdsu.edu |
|
200623 15:00 |